数据结构—树表的查找
7.3树表的查找
当表插入、删除操作频繁时,为维护表的有序表,需要移动表中很多记录。
改用动态查找表——几种特殊的树
表结构在查找过程中动态生成
对于给定值key
若表中存在,则成功返回;
否则,插入关键字等于key的记录
7.3.1二叉排序树
二叉排序树(Binary Sort Tree)又称为二叉搜索树、二叉查找树。
定义:
二叉排序树或是空树,或是满足如下性质的二叉树:(1)若其左子树非空,则左子树上所有结点的值均小于根结点的值;(2)若其右子树非空,则右子树上所有结点的值均大于等于根结点的值;(3)其左右子树本身又各是一棵二叉树
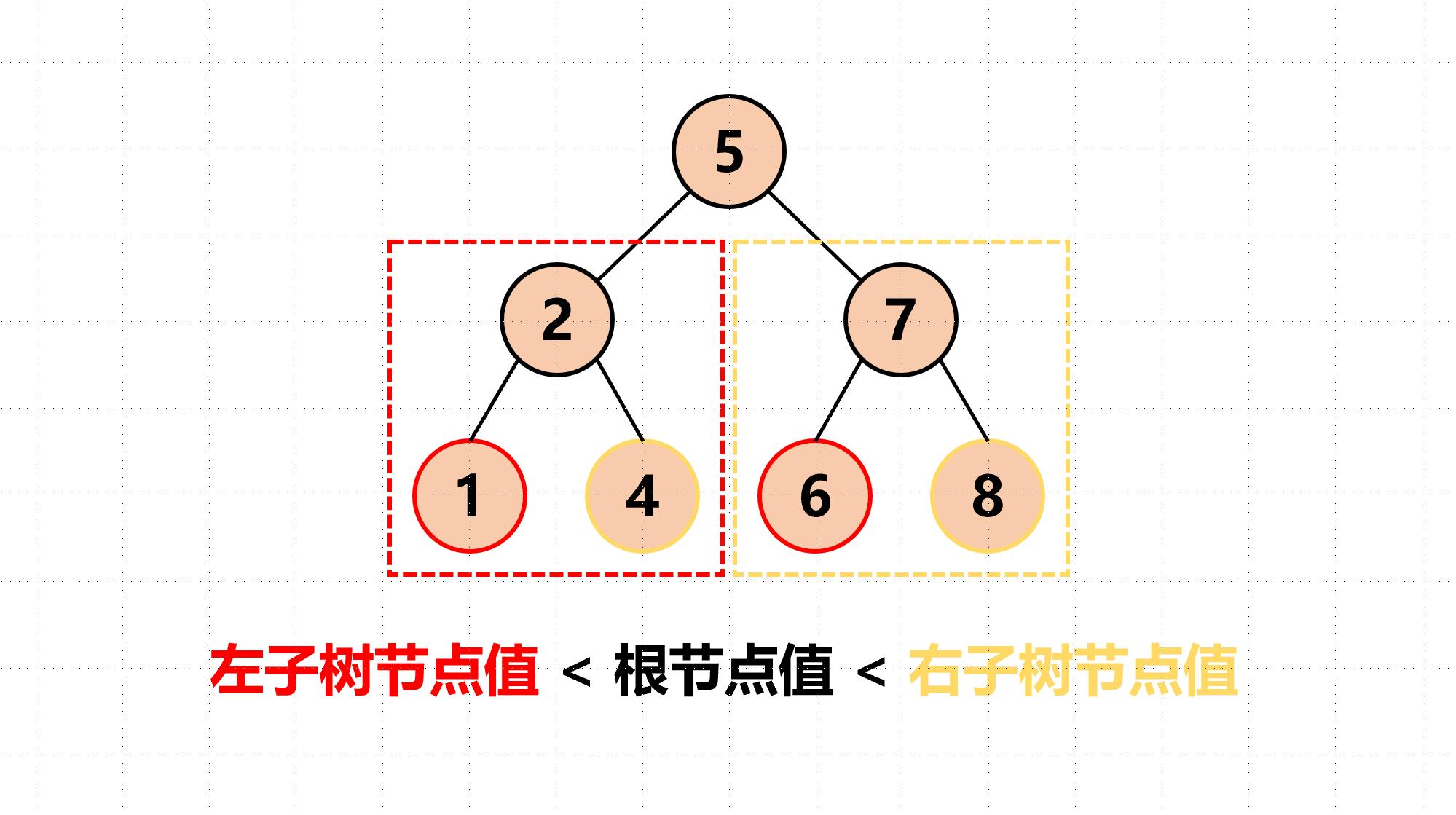
二叉排序树的性质:
中序遍历非空的二叉排序树所得的数据元素序列时一个按关键字排序的递增有序序列。
二叉排序树的存储结构
typedef struct{KeyType key;//关键字项InfoType otherinfo;//其他数据域
}ElemType;
typedef struct BSTNode{ElemType data;//数据域struct BSTNode *lchild,*rchild;//左右孩子指针
}BSTree T;
BSTree T;//定义二叉排序树
查找
- 若查找的关键字等于根结点,成功
- 否则
- 若小于根结点,查其左子树
- 若大于根结点,查其右子树
- 在左右子树上的操作类似
1、二叉排序树的递归查找
【算法思想】
- 若二叉排序树为空,则查找失败,返回空指针。
- 若二叉排序树非空,将给定值key与根结点的关键字T->data.key进行比较:
- 若key等于T->data.key,则查找成功,返回根结点地址;
- 若key小于T->data.key,则进一步查找左子树;
- 若key大于T->data.key,则进一步查找左子树。
BSTree SerachBT(BSTree T,KeyType key){if((!T)||key==T->data.key) return T;else if(key<T->data.key)return SearchBST(T->lchild,key);//在左子树中继续查找else return SearchBST(T->rchild,key);//在右子树中继续查找
}
二叉排序树的查找分析
二叉排序树上查找某关键字等于给定值的结点过程,其实就是走了一条从根到该结点的路径。
比较的关键字次数=此结点所在层次数
最多的比较次数=数的深度
问题:如何提高形态不均衡的二叉排序树的查找效率?
解决办法:做“平衡化”处理,即尽量让二叉树的形状均衡!
2、二叉排序树的插入
- 若二叉排序树为空,则插入结点作为根结点插入到空树中
- 否则,继续在其左、右子树上查找
- 树中已有,不再插入
- 树中没有
- 查找直至某个叶子结点的左子树或右子树为空为止,则插入结点应为该叶子结点的左孩子或右孩子。
插入的元素一定在叶节点上
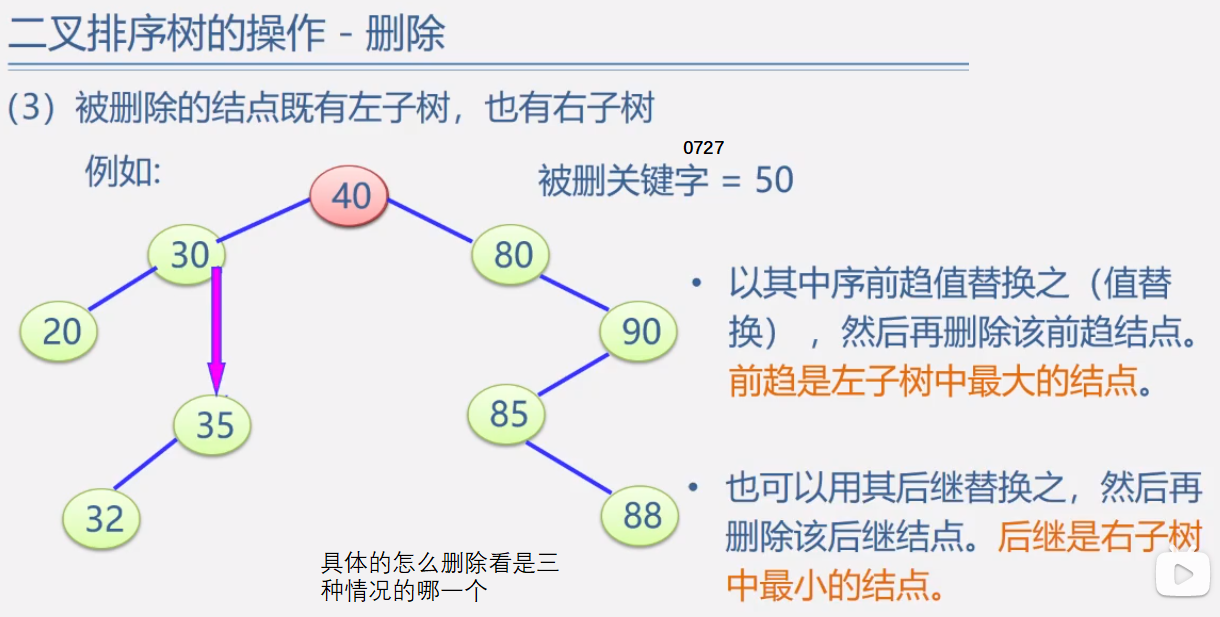
3、二叉排序树的删除
从二叉排序树中删除一个结点,不能把以该结点为根的子树都删去,只能删掉该结点,并且还应保证删除后所得的二叉树仍然满足二叉排序树的性质不变。
由于中序遍历二叉排序树可以得到一个递增有序的序列。那么,在二叉排序树删去一个结点相当于删去有序序列中的一个结点。
- 将因删除结点而断开的二叉链表重新链接起来
- 防止重新链接后树的高度增加

4、二叉排序树的生成
从空树出发,经过一系列的查找、插入操作之后,可生成一棵二叉排序树。
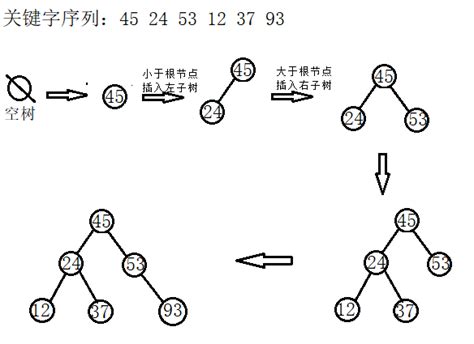
一个无序序列可通过构造二叉排序树而变成一个有序序列。构造树的过程就是对无序序列进行排序的过程。
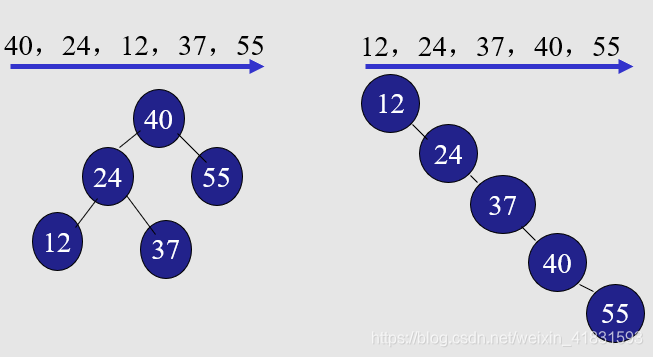
插入的结点均为叶子结点,故无序移动其他结点。相当于在有序序列上插入记录而无需移动其他记录。
关键字的输入顺序不同,建立的二叉排序树不同
7.3.2平衡二叉树
1.平衡二叉树的定义
平衡二叉树(balance binary tree)
-
又称AVL树
-
一棵平衡二叉树或者是空树,或者是具有下列性质的二叉排序树:
- 左子树与右子树的高度之差的绝对值小于等于1;
- 左子树和右子树也是平衡二叉排序树。
为了方便起见,给每个结点附加一个数字,给出该结点左子树与右子树的高度差。这个数字称为结点的平衡因子(BF)。
平衡因子 = 结点左子树的高度 - 结点右子树的高度
根据平衡二叉树的定义,平衡二叉树上所有结点的平衡因子只能是-1、0或1。
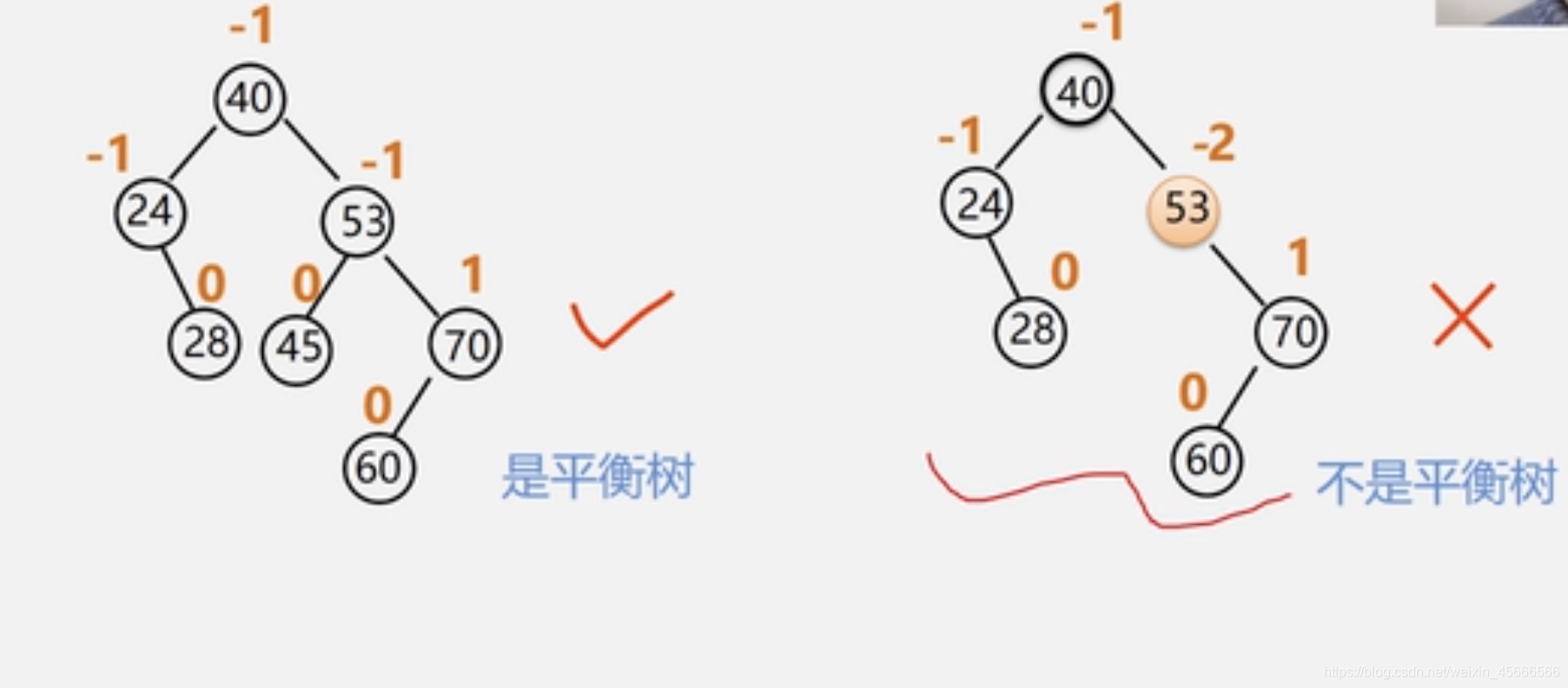
2.失衡二叉排序树的分析与调整
当我们在一个平衡二叉排序树上插入一个结点时,有可能导致失衡,即出现平衡因子绝对值大于1的结点,如:2、-2。
如果在一棵AVL树中插入一个新结点后造成失衡,则必须重新调整树的结果,使之恢复平衡。
相关文章:

数据结构—树表的查找
7.3树表的查找 当表插入、删除操作频繁时,为维护表的有序表,需要移动表中很多记录。 改用动态查找表——几种特殊的树 表结构在查找过程中动态生成 对于给定值key 若表中存在,则成功返回; 否则࿰…...

微信小程序测试策略和注意事项?
一、测试前准备(环境搭建) 1、前端页面 微信 Web 开发者工具安装、授权测试用的微信号可预览和调试小程序 2、管理后台 配置内网测试服务器环境,通过 PC 端 Web 站点管理小程序前端的输出内容,可从开发人员获取管理账号进行测…...

VUE3封装EL-ELEMENT-PLUS input组件
VUE3封装EL-ELEMENT-PLUS input组件 完整代码 <template><div><div><div class"lable_top" v-if"label"><label :class"lable_sty">{{ label }}</label></div><el-inputv-model"inputValue&…...

RISC-V公测平台发布 · 在SG2042上配置Jupiter+Octave科学计算环境
简介 JupyterHub是一个开源的共享计算平台,它为每个用户管理一个单独的 Jupyter 环境, 可以用于学生班级、企业数据科学小组或科学研究小组。它是一个多用户中心,可以生成、管理和代理多个单用户Jupyter笔记本服务器的实例。 GNU Octave是一…...
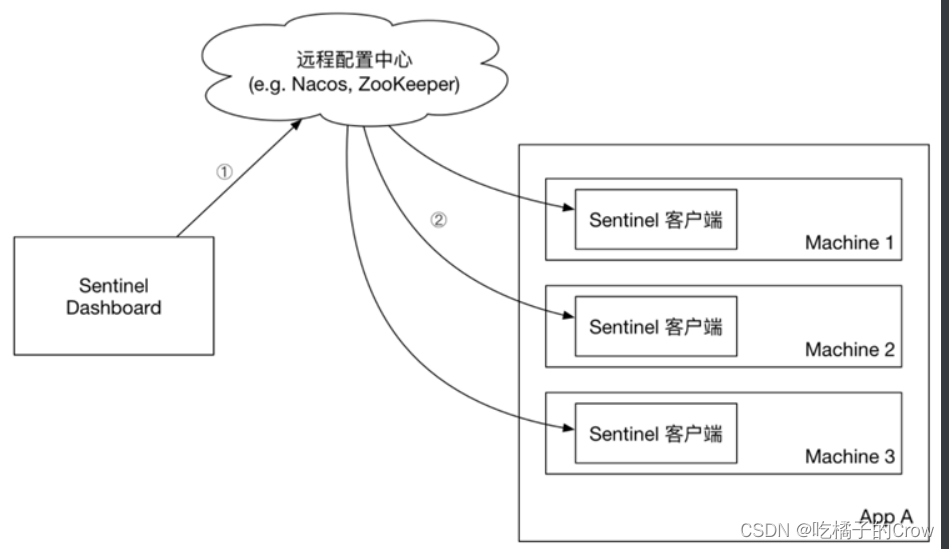
初识Sentinel
目录 1.解决雪崩的方式有4种: 1.1.2超时处理: 1.1.3仓壁模式 1.1.4.断路器 1.1.5.限流 1.1.6.总结 1.2.服务保护技术对比 1.3.Sentinel介绍和安装 1.3.1.初识Sentinel 1.3.2.安装Sentinel 1.4.微服务整合Sentinel 2.流量控制 2.1.簇点链路 …...

【官方中文文档】Mybatis-Spring #注入映射器
注入映射器 与其在数据访问对象(DAO)中手工编写使用 SqlSessionDaoSupport 或 SqlSessionTemplate 的代码,还不如让 Mybatis-Spring 为你创建一个线程安全的映射器,这样你就可以直接注入到其它的 bean 中了: <bea…...
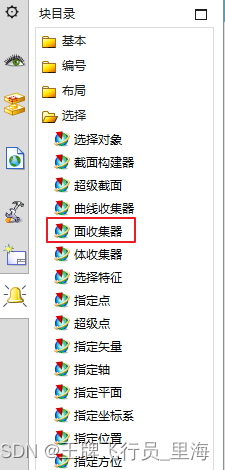
UG\NX 二次开发 相切面、相邻面的选择控件
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan 简介: 有群友问“UFUN多选功能过滤面不能选择相切面或相邻面之类的吗?” 这个用Block UI的"面收集器"就可以,ufun函数是不行的。 效果: C++语言在UG二次开发中的应用及综合分析 C++ …...
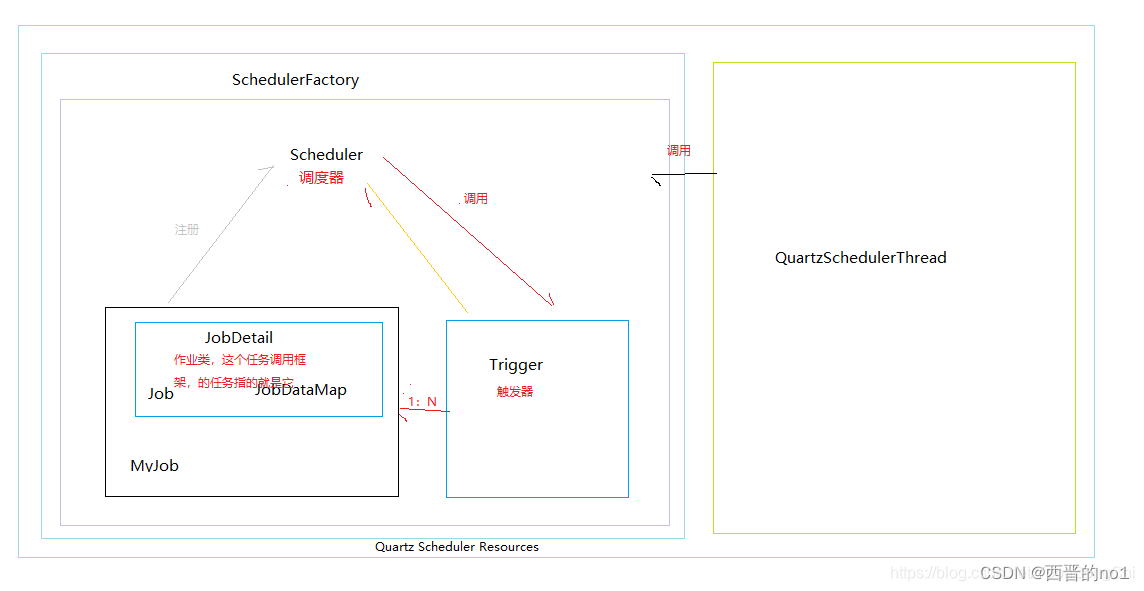
Quartz任务调度框架介绍和使用
一、Quartz介绍 Quartz [kwɔːts] 是OpenSymphony开源组织在Job scheduling领域又一个开源项目,完全由Java开发,可以用来执行定时任务,类似于java.util.Timer。但是相较于Timer, Quartz增加了很多功能: 1.持久性作业 …...
drools8尝试
drools7升级到drools8有很大很大的变更.几乎不能说是一个项目了. 或者说就是名字相同的不同项目, 初看下来变化是这样 两个最关键的东西都retired了 https://docs.drools.org/8.42.0.Final/drools-docs/drools/migration-guide/index.html business central变成了一个VS code…...
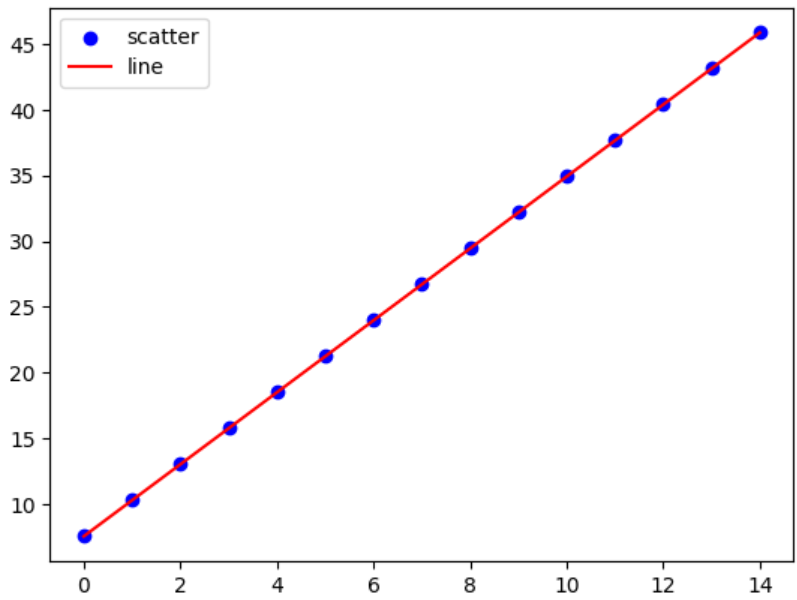
【机器学习】python基础实现线性回归
手写梯度下降的实现ykxb的线性回归 算法步骤: (1)构造数据,y3*x5; (2)随机初始化和,任意数值,例如9,10; (3)计算,,并计算 (4&…...
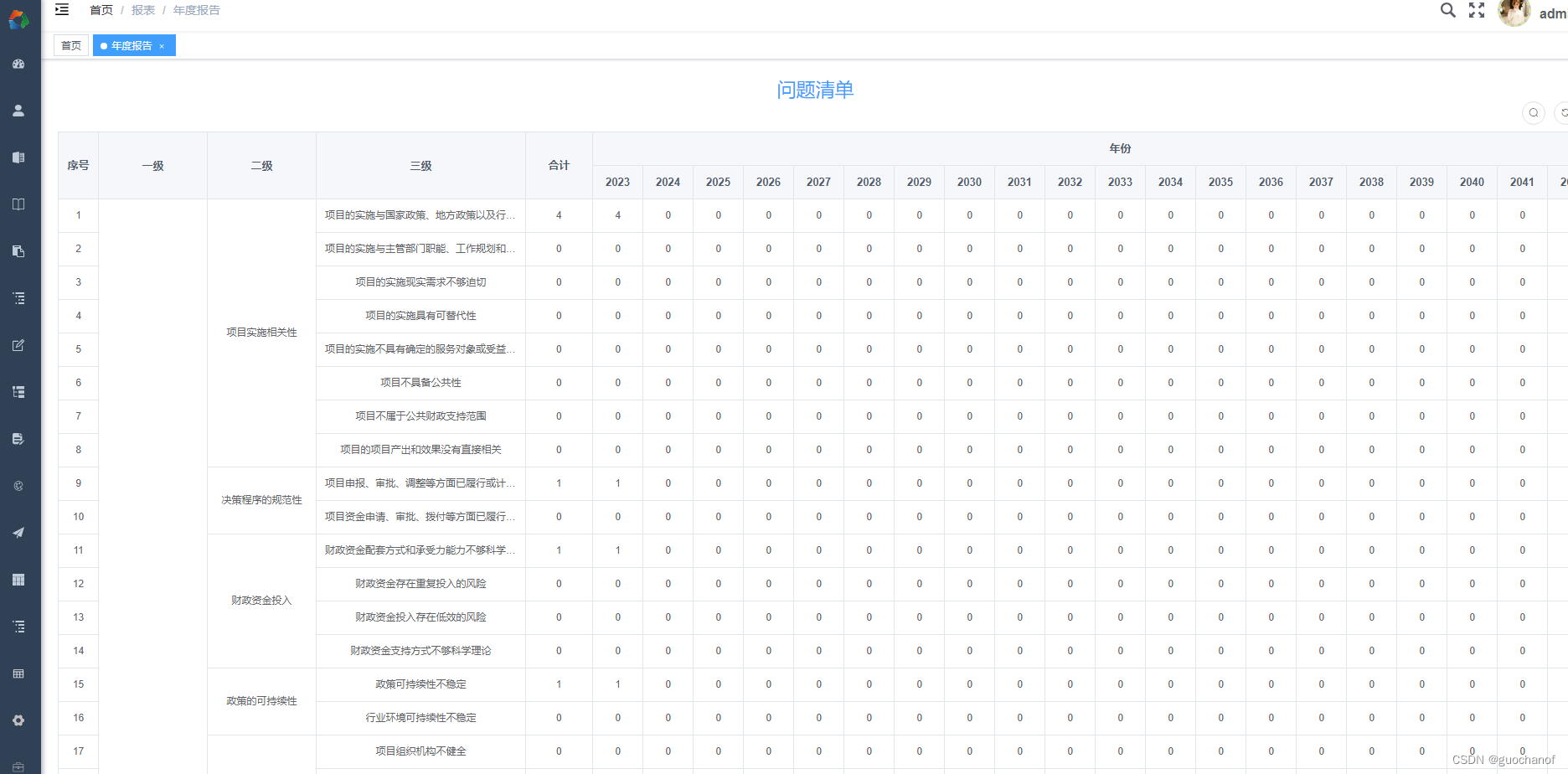
vue table合并行 动态列名
需求: 1.合并行,相同数据合并 2,根据后端返回数据动态显示列名, 我这个业务需求是,每年增加一列,也就是列名不是固定的,后端返回数据每年会多一条数据,根据返回数据显示列名 实现: html <el-table v-loading"loading" :data"dataList" :span-metho…...
Spring Cloud Alibaba-Nacos Discovery--服务治理
1 服务治理介绍 先来思考一个问题 通过上一章的操作,我们已经可以实现微服务之间的调用。但是我们把服务提供者的网络地址 (ip,端口)等硬编码到了代码中,这种做法存在许多问题: 一旦服务提供者地址变化&am…...

【C++】unordered_map和unordered_set的使用 及 OJ练习
文章目录 前言1. unordered系列关联式容器2. map、set系列容器和unordered_map、unordered_set系列容器的区别3. unordered_map和unordered_set的使用4. set与unordered_set性能对比5. OJ练习5.1 在长度 2N 的数组中找出重复 N 次的元素思路分析AC代码 5.2 两个数组的交集思路分…...
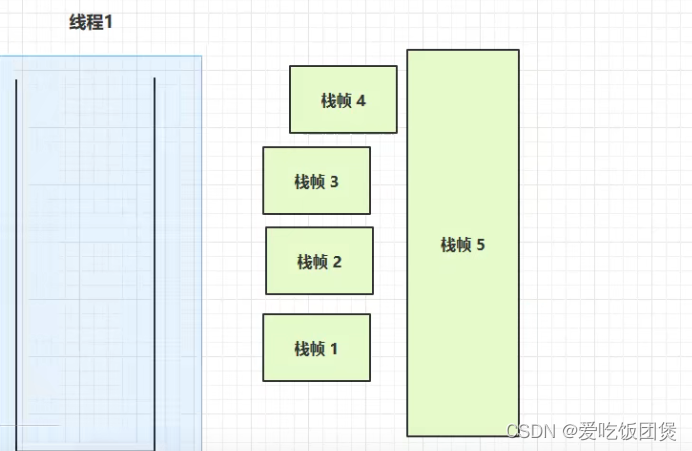
初识 JVM 01
JVM JRE JDK的关系 JVM 的内存机构 程序计数器 java指令的执行流程: 1 右侧的java源代码编译为左侧的java字节码(右侧第一个方块对应左侧第一个方块) 2 字节码 经过解释器 变为机器码 3 机器码就可以被cpu来执行 程序计数器的作用就…...

FPGA应用学习笔记----I2S和总结
时序一致在慢时序方便得多 增加了时序分布和分析的复杂性 使用fifo会开销大量资源...
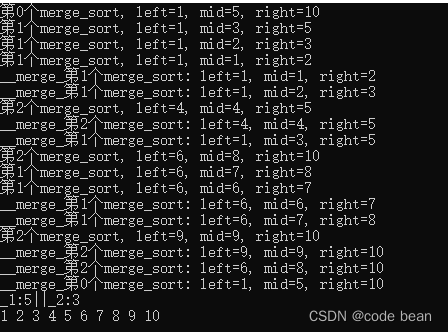
归并排序之从微观看递归
前言 这次,并不是具体讨论归并排序算法,而是利用归并排序算法,探讨一下递归。归并排序的特点在于连续使用了两次递归调用,这次我们将从微观上观察递归全过程,从本质上理解递归,如果能看完,你一…...

Pytorch-day07-模型保存与读取
PyTorch 模型保存&读取 模型存储模型单卡存储&多卡存储模型单卡读取&多卡读取 1、模型存储 PyTorch存储模型主要采用pkl,pt,pth三种格式,就使用层面来说没有区别PyTorch模型主要包含两个部分:模型结构和权重。其中模型是继承n…...

【C语言每日一题】01. Hello, World!
题目来源:http://noi.openjudge.cn/ch0101/01/ 01. Hello, World! 总时间限制: 1000ms 内存限制: 65536kB 问题描述 对于大部分编程语言来说,编写一个能够输出“Hello, World!”的程序往往是最基本、最简单的。因此,这个程序常常作为一个初…...
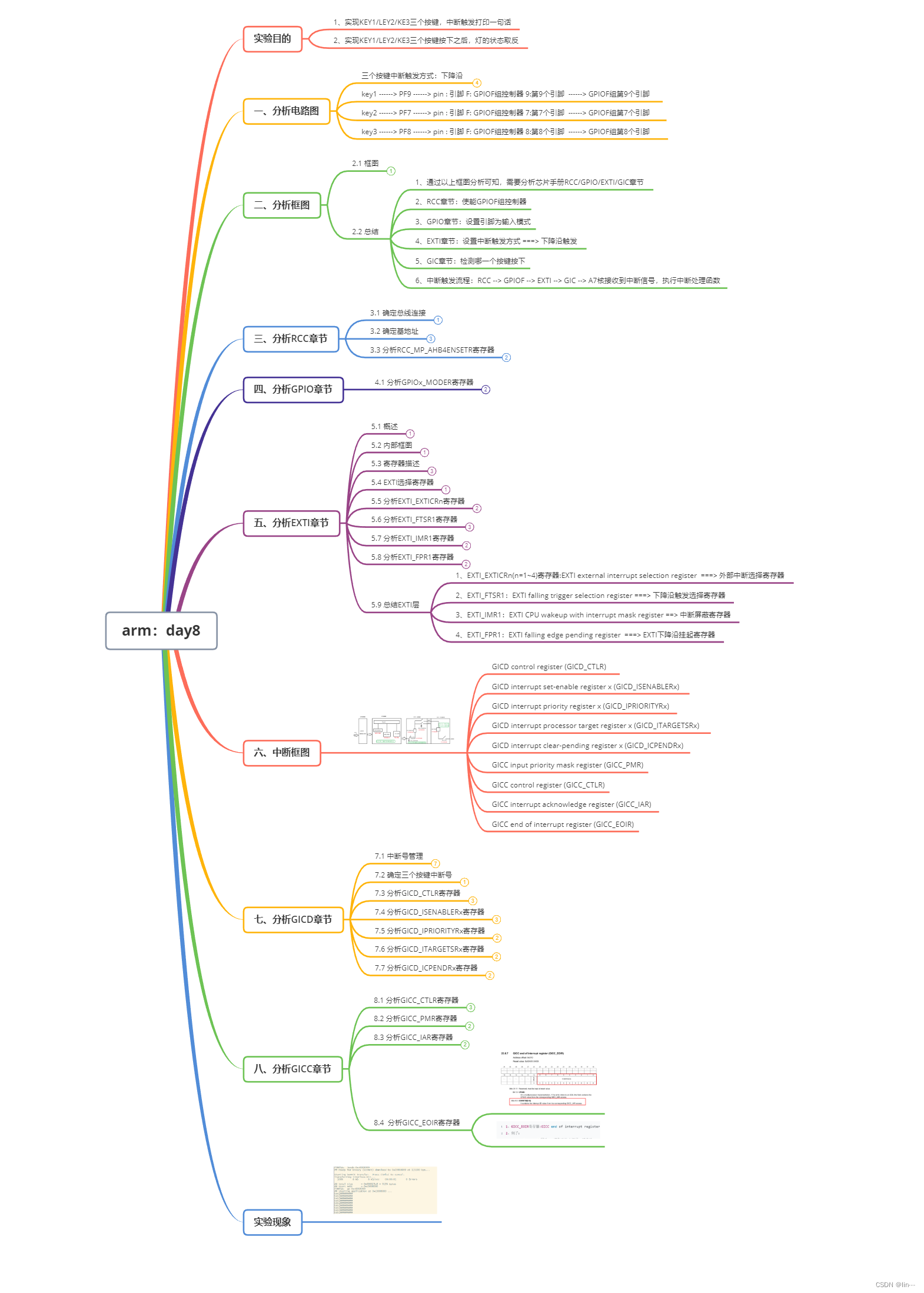
arm: day8
1.中断实验:按键控制led灯 流程: key.h /*************************************************************************> File Name: include/key.h> Created Time: 2023年08月21日 星期一 17时03分20秒***************************************…...

k8s容器加入host解析字段
一、通过edit或path来修改 kubectl edit deploy /xxxxx. x-n cattle-system xxxxx为你的资源对象名称 二、添加字段 三、code hostAliases:- hostnames:- www.rancher.localip: 10.10.2.180...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
