AVL——平衡搜索树
✅<1>主页:我的代码爱吃辣
📃<2>知识讲解:数据结构——AVL树
☂️<3>开发环境:Visual Studio 2022
💬<4>前言:AVL树是对二叉搜索树的严格高度控制,所以AVL树的搜索效率很高,但是这是需要付出很大的代价的,要维护父亲指针,和平衡因子。
目录
一.AVL的概念
二. AVL树节点及整体结构的定义
三. AVL树的插入
1. 先按照二叉搜索树的规则将节点插入到AVL树中
2.根据插入的位置调整平衡因子
四.AVL树的旋转
1.左单旋
2.右单旋
3.左右双旋
4.右左双旋
5.总结:
五.AVL树的删除(了解)
六.AVL树的性能
七.完整代码及测试

一.AVL的概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查
找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii
和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
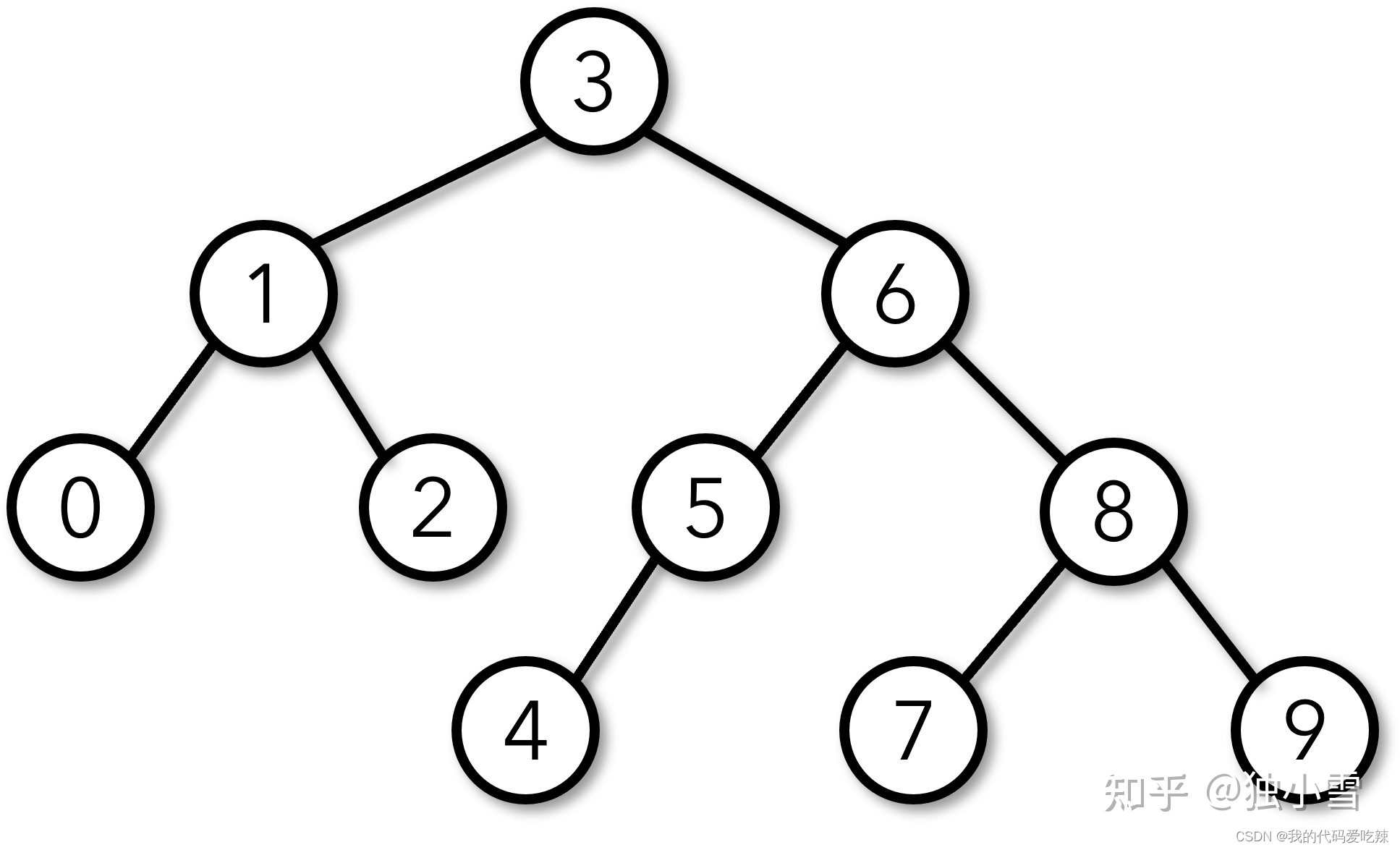
如果一棵二叉搜索树是高度平衡的,它就是AVL树。如果它有n个结点,其高度可保持在
O(),搜索时间复杂度O(
)
二. AVL树节点及整体结构的定义
//AVL树结点
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode(pair<K,V> kv):_kv(kv),_bf(0),_left(nullptr),_right(nullptr),_parent(nullptr){}pair<K, V> _kv; //Key/Value数据int _bf; //平衡因子AVLTreeNode<K, V>* _left; //结点的左子树AVLTreeNode<K, V>* _right; //结点的右子树AVLTreeNode<K, V>* _parent; //结点的双亲
};//AVL树定义
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool insert(pair<K,V> kv){}
private:Node* _root = nullptr;
};三. AVL树的插入
AVL树就是在二叉搜索树的基础上引入了平衡因子,因此AVL树也可以看成是二叉搜索树。那么
AVL树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点
- 调整节点的平衡因子
插入过程:
1. 先按照二叉搜索树的规则将节点插入到AVL树中
bool insert(pair<K,V> kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;//记录当前结点Node* parent = nullptr;//记录父亲结点while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}//找到了合适的位置,创建新节点,出入位置cur = new Node(kv);//修改新节点的指向if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//未完待续....}2.根据插入的位置调整平衡因子
平衡因子:右子树高度减去左子树高度。
cur 插入后,parent 的平衡因子一定需要调整,在插入之前,pParent 的平衡因子分为三种情况:-1,0, 1, 分以下两种情况:
- 如果cur插入到parent的左侧,只需给parent的平衡因子-1即可
- 如果cur插入到parent的右侧,只需给parent的平衡因子+1即可
此时:parent的平衡因子可能有三种情况:0,正负1, 正负2
- 如果parent的平衡因子为0,说明插入之前parent的平衡因子为正负1,插入后被调整成0,此时满足 AVL树的性质,插入成功。
- 如果parent的平衡因子为正负1,说明插入前parent的平衡因子一定为0,插入后被更新成正负1,此 时以parent为根的树的高度增加,需要继续向上更新。
- 如果parent的平衡因子为正负2,则parent的平衡因子违反平衡树的性质,需要对其进行旋转处理。
while (parent){//cur插入到parent的左侧if (parent->_left == cur){parent->_bf--;}else//cur插入到parent的右侧{parent->_bf++;}//需向上调整平衡因子if (parent->_bf == 1||parent->_bf==-1){cur = parent;parent = cur->_parent;}//无需向上调整平衡因子else if(parent->_bf==0){break;}//无需向上调整平衡因子,直接旋转处理else if (parent->_bf == 2||parent->_bf==-2){//旋转,旋转之后平衡因子已经平衡,可以直接推出break;}else//出现的其他的错误情况{assert(0);}}四.AVL树的旋转
如果在一棵原本是平衡的AVL树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,
使之平衡化。根据节点插入位置的不同,AVL树的旋转分为四种:
1.左单旋
新节点插入较高右子树的右侧
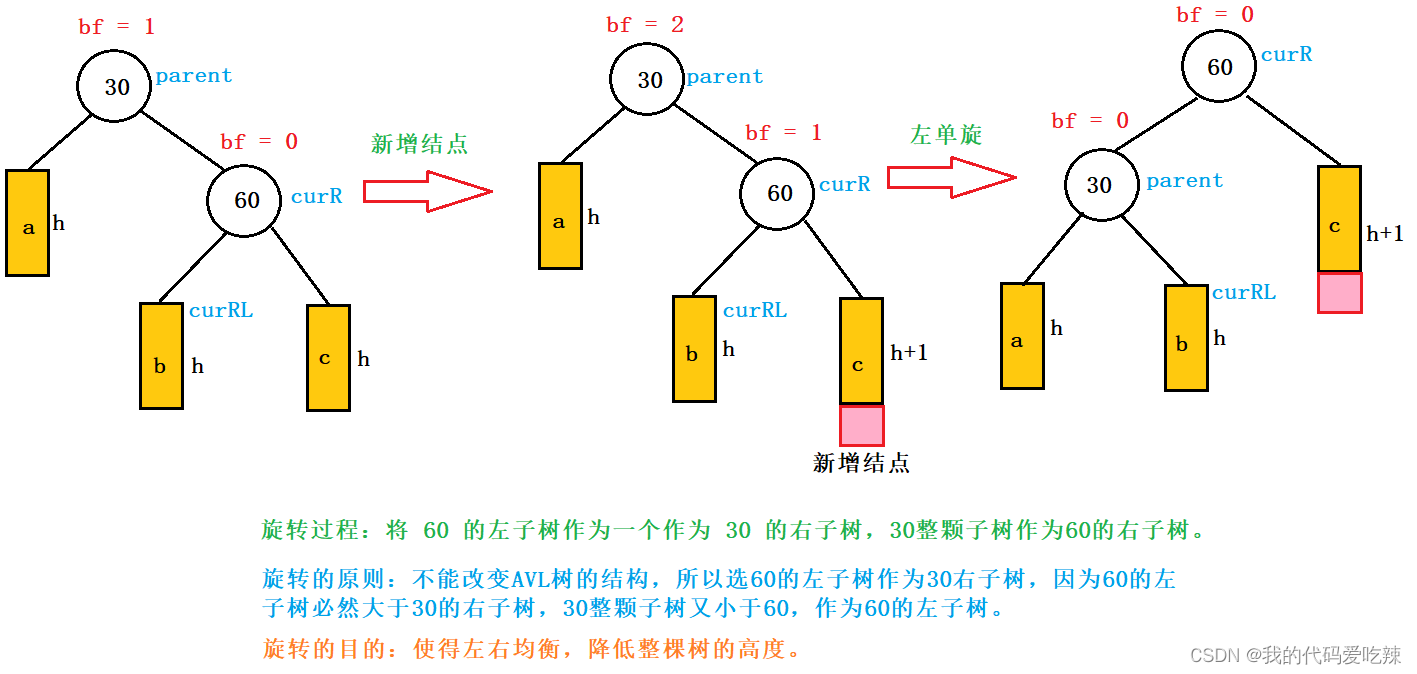
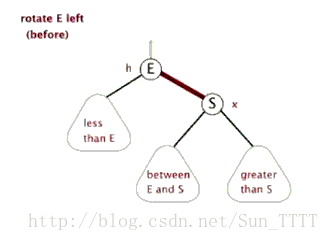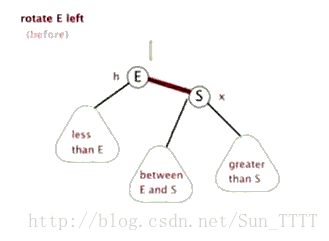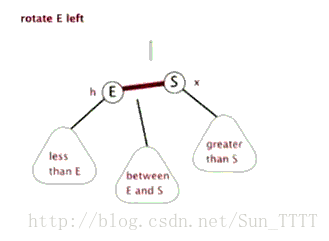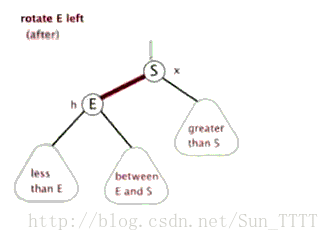
上图在插入前,AVL树是平衡的,新节点插入到60的右子树中,30右子树增加了一层,导致以60为根的二叉树不平衡,要让30平衡,只能将30右子树的高度减少一层,左子树增加一层,即将右子树往上提,这样30转下来,因为30比60小,只能将其放在60的左子树,而如果60有左子树,左子树根的值一定大于30,小于60,只能将其放在30的右子树,旋转完成后,更新节点的平衡因子即可。在旋转过程中,有以下几种情况需要考虑:
- 60节点的左孩子可能存在,也可能不存在。
- 30可能是整棵树根节点,也可能是子树根节点。
如果是整棵树根节点,旋转完成后,要更整棵树新根节点;如果是子树根节点,可能是某个节点的左子树,也可能是右子树。
void RotateL(Node* parent){// a// b// c//找到需要旋转的结点Node* curR = parent->_right;Node* curRL = curR->_left;//调整结点,并且修改其父亲结点指针parent->_right = curRL;if (curRL)//可能为空{curRL->_parent = parent;}//在修改子树根节点之前,保存子树根节点的父亲Node* pparent = parent->_parent;//修改子树根节点curR->_left = parent;parent->_parent = curR;//子树根节点有可能是整棵树的根节点if (pparent == nullptr){_root = curR;_root->_parent = nullptr;}else//子树根节点不是整棵树的根节点{//还要看子树是它父亲的左孩子还是右孩子if (pparent->_left == parent){pparent->_left = curR;}else{pparent->_right = curR;}}//修改平衡因子curR->_bf = parent->_bf = 0;}2.右单旋
新节点插入较高左子树的左侧
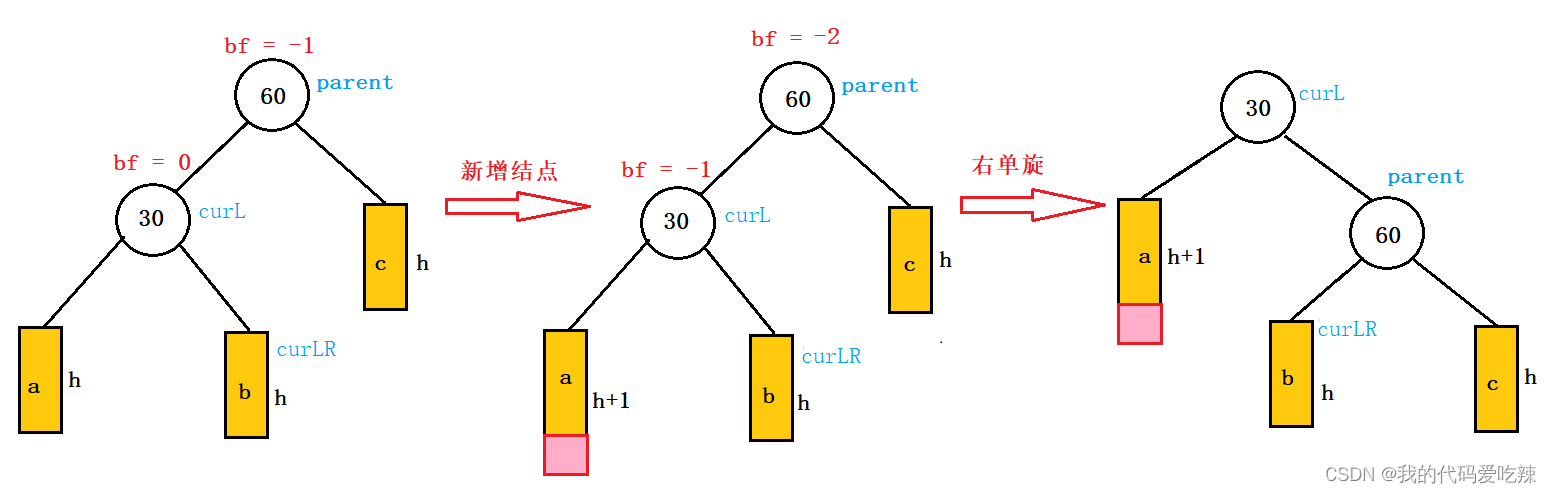
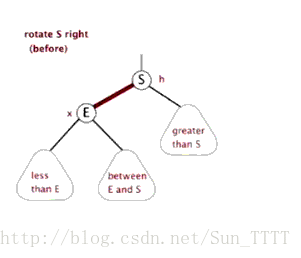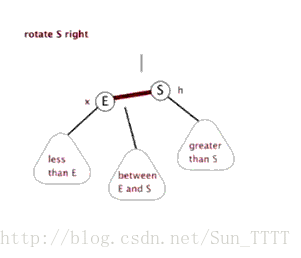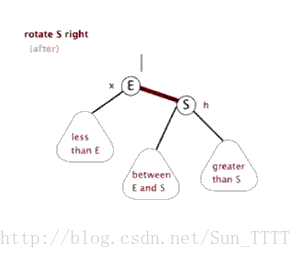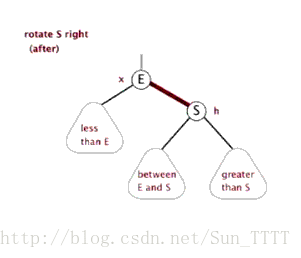
右单旋过程和左单旋转过程一模一样仅仅只是反过来。
void RotateR(Node* parent){Node* curL = parent->_left;Node* curLR = curL->_right;parent->_left = curLR;if (curLR){curLR->_parent = parent;}Node* pparent = parent->_parent;curL->_right = parent;parent->_parent = curL;if (pparent == nullptr){_root = curL;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = curL;}else{pparent->_right = curL;}}curL->_bf = parent->_bf = 0;}3.左右双旋
新节点插入较高左子树的右侧---左右:先左单旋再右单旋
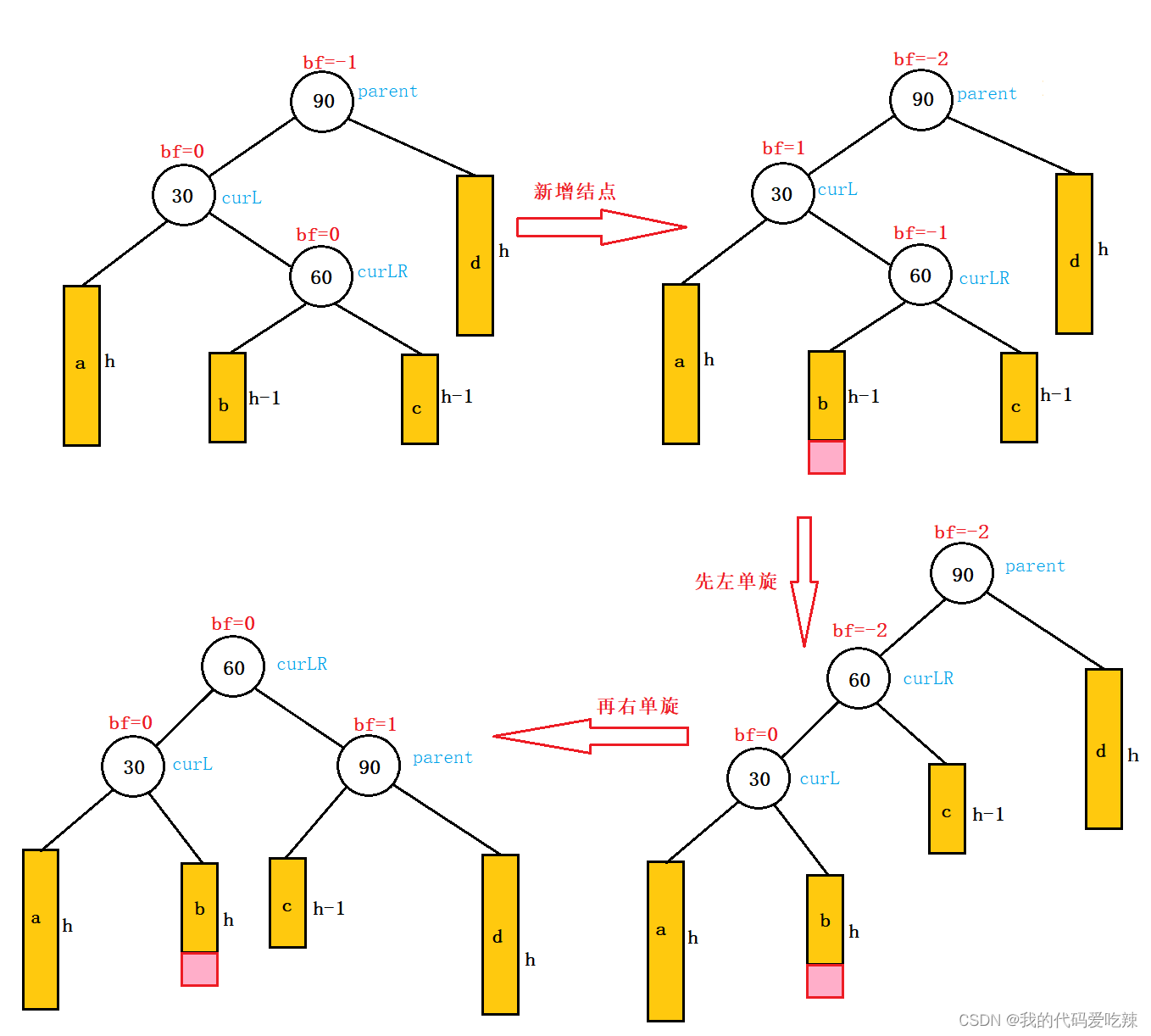
将双旋变成单旋后再旋转,即:先对30进行左单旋,然后再对90进行右单旋,旋转完成后再
考虑平衡因子的更新。
注意:旋转之前,60的平衡因子可能是 -1 / 0 / 1,旋转完成之后,根据情况对其他节点的平衡因子进行调整。
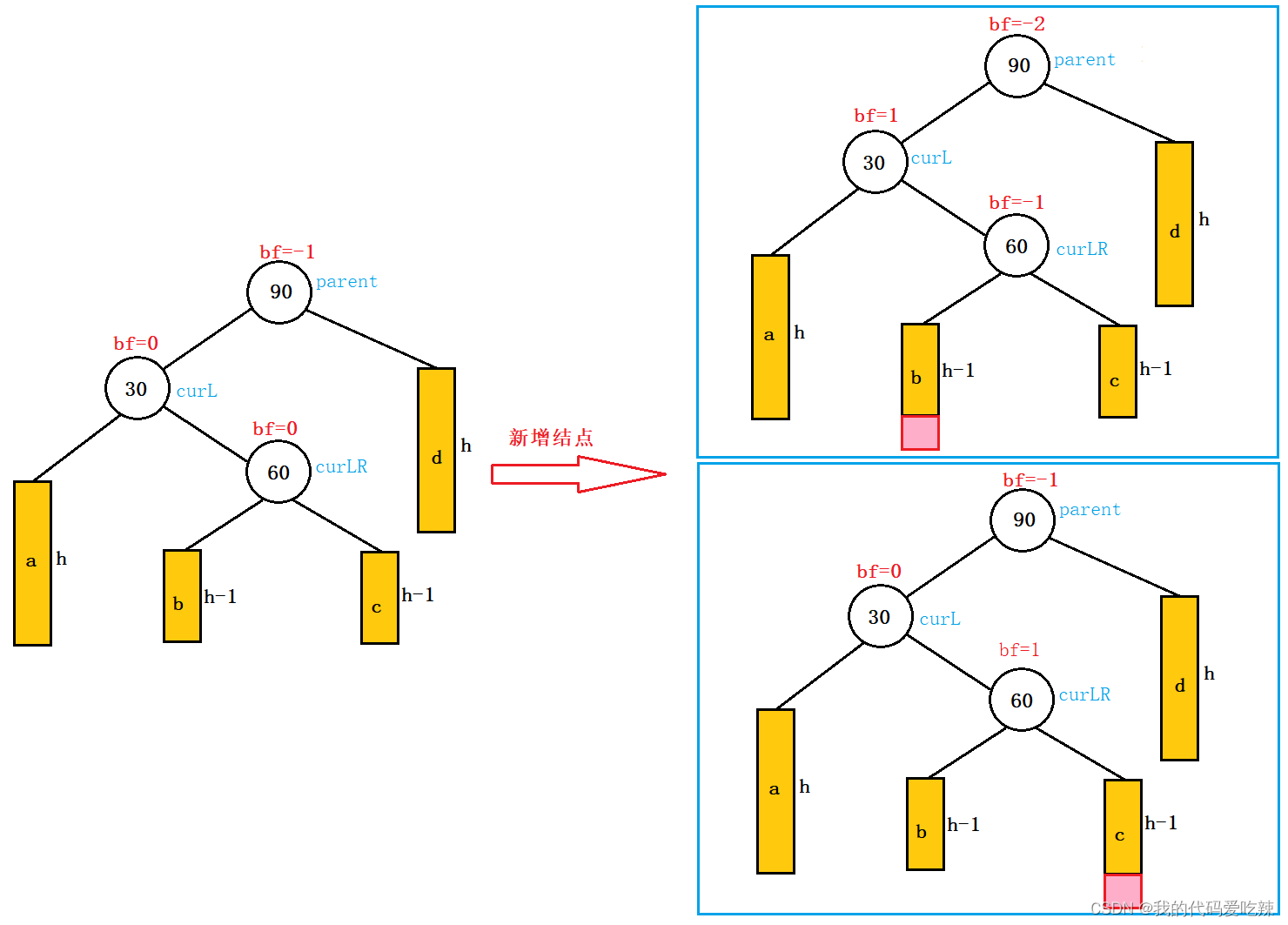
当h=0,时60自己就是一个新插入的结点,此时他的平衡因子就是。
所以旋转之前,需要保存curLR的平衡因子,旋转完成之后,需要根据该平衡因子来调整其他节
点的平衡因子。
4.右左双旋
右左双旋和左右双旋过程一模一样,仅仅只是反过来。
void RotateRL(Node* parent){Node* curR = parent->_left;Node* curRL = curR->_right;int curRL_bf = curRL->_bf;RotateL(curR);RotateR(parent);if (curRL_bf == -1){parent->_bf = 0;curRL->_bf = 0;curR->_bf = 1;}else if (curRL_bf == 1){parent->_bf = -1;curRL->_bf = 0;curR->_bf = 1;}else if (curRL_bf == 0){parent->_bf = 0;curRL->_bf = 0;curR->_bf = 0;}else{assert(false);}}
5.总结:
假如以parent为根的子树不平衡,即parent的平衡因子为2或者-2,分以下情况考虑
1. parent的平衡因子为2,说明parent的右子树高,设parent的右子树的根为curR
- 当curR的平衡因子为1时,执行左单旋
- 当curR的平衡因子为-1时,执行右左双旋
2. parent的平衡因子为-2,说明parent的左子树高,设parent的左子树的根为curL
- 当curL的平衡因子为-1是,执行右单旋
- 当curL的平衡因子为1时,执行左右双旋
旋转完成后,原parent为根的子树个高度降低,已经平衡,不需要再向上更新。
//调整平衡因子while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 1||parent->_bf==-1)//需向上调整平衡因子{cur = parent;parent = cur->_parent;}else if(parent->_bf==0)//无需向上调整平衡因子{break;}else if (parent->_bf == 2||parent->_bf==-2)//无需向上调整平衡因子,直接旋转{if (parent->_bf == 2 && parent->_right->_bf == 1){RotateL(parent);//左单旋}else if (parent->_bf == -2 && parent->_left->_bf == -1){RotateR(parent);//右单旋}else if (parent->_bf == 2 && parent->_left->_bf == -1){RotateRL(parent);//右左双旋}else if (parent->_bf == -2 && parent->_left ->_bf== 1){RotateLR(parent);//左右双旋}else{assert(false);//其他错误情况}break;}else{assert(0);}五.AVL树的删除(了解)
因为AVL树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不
错与删除不同的时,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。
具体实现学生们可参考《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。
六.AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这
样可以保证查询时高效的时间复杂度,即。但是如果要对AVL树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此:如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合。
七.完整代码及测试
AVL.hpp
#pragma once
#include<iostream>
#include<cassert>
using namespace std;template<class K, class V>
struct AVLTreeNode
{AVLTreeNode(pair<K,V> kv):_kv(kv),_bf(0),_left(nullptr),_right(nullptr),_parent(nullptr){}pair<K, V> _kv; //Key/Value数据int _bf; //平衡因子AVLTreeNode<K, V>* _left; //结点的左子树AVLTreeNode<K, V>* _right; //结点的右子树AVLTreeNode<K, V>* _parent; //结点的双亲
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool insert(pair<K,V> kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else{return false;}}//找到了合适的位置cur = new Node(kv);//if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;//调整平衡因子while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 1||parent->_bf==-1)//需向上调整平衡因子{cur = parent;parent = cur->_parent;}else if(parent->_bf==0)//无需向上调整平衡因子{break;}else if (parent->_bf == 2||parent->_bf==-2)//无需向上调整平衡因子,直接旋转{if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);//左单旋}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);//右单旋}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);//右左双旋}else if (parent->_bf == -2 && cur ->_bf== 1){RotateLR(parent);//左右双旋}else{//cout << parent->_bf << ":" << /*parent->_left->_bf << ":" <<*/ parent->_right->_bf << endl;assert(false);//其他错误情况}break;}else{assert(false);}}return true;}void Inorder(){_inorder(_root);cout << endl;}private:void _inorder(Node* root){if (root == nullptr){return;}_inorder(root->_left);cout << root->_kv.first << " ";_inorder(root->_right);}void RotateL(Node* parent){// a// b// c//找到需要旋转的结点Node* curR = parent->_right;Node* curRL = curR->_left;//调整结点,并且修改其父亲结点指针parent->_right = curRL;if (curRL)//可能为空{curRL->_parent = parent;}//在修改子树根节点之前,保存子树根节点的父亲Node* pparent = parent->_parent;//修改子树根节点curR->_left = parent;parent->_parent = curR;//子树根节点有可能是整棵树的根节点if (pparent == nullptr){_root = curR;_root->_parent = nullptr;}else//子树根节点不是整棵树的根节点{//还要看子树是它父亲的左孩子还是右孩子if (pparent->_left == parent){pparent->_left = curR;}else{pparent->_right = curR;}curR->_parent = pparent;}//修改平衡因子curR->_bf = parent->_bf = 0;}void RotateR(Node* parent){Node* curL = parent->_left;Node* curLR = curL->_right;parent->_left = curLR;if (curLR){curLR->_parent = parent;}Node* pparent = parent->_parent;curL->_right = parent;parent->_parent = curL;if (parent == _root){_root = curL;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = curL;}else{pparent->_right = curL;}curL->_parent = pparent;}curL->_bf = parent->_bf = 0;}void RotateLR(Node* parent){Node* curL = parent->_left;Node* curLR = curL->_right;//旋转之前,保存pSubLR的平衡因子,旋转完成之后,//需要根据该平衡因子来调整其他节点的平衡因子int curLR_bf = curLR->_bf;//RotateL(curL);RotateR(parent);if (curLR_bf == -1){parent->_bf = 1;curLR->_bf = 0;curL->_bf = 0;}else if (curLR_bf == 1){parent->_bf = 0;curL->_bf = -1;curLR->_bf = 0;}else if (curLR_bf == 0){parent->_bf = 0;curL->_bf = 0;curLR->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent){Node* curR = parent->_right;Node* curRL = curR->_left;int curRL_bf = curRL->_bf;RotateR(curR);RotateL(parent);if (curRL_bf == -1){parent->_bf = 0;curRL->_bf = 0;curR->_bf = 1;}else if (curRL_bf == 1){parent->_bf = -1;curRL->_bf = 0;curR->_bf = 0;}else if (curRL_bf == 0){parent->_bf = 0;curRL->_bf = 0;curR->_bf = 0;}else{assert(false);}}Node* _root = nullptr;
};test.cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include"AVL.hpp"
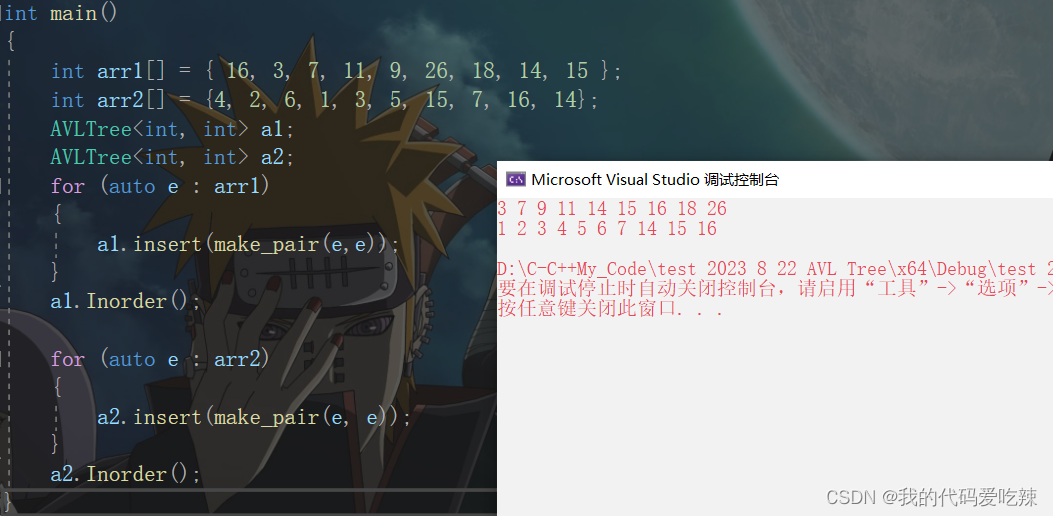
int main()
{int arr1[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int arr2[] = {4, 2, 6, 1, 3, 5, 15, 7, 16, 14};AVLTree<int, int> a1;AVLTree<int, int> a2;for (auto e : arr1){a1.insert(make_pair(e,e));}a1.Inorder();for (auto e : arr2){a2.insert(make_pair(e, e));}a2.Inorder();
}
相关文章:

AVL——平衡搜索树
✅<1>主页:我的代码爱吃辣📃<2>知识讲解:数据结构——AVL树☂️<3>开发环境:Visual Studio 2022💬<4>前言:AVL树是对二叉搜索树的严格高度控制,所以AVL树的搜索效率很高…...

TCP通信流程以及一些TCP的相关概念
1.TCP和UDP区别 都为传输层协议 UDP:用户数据报协议,面向无连接,可以单播,多播,广播,面向数据报,不可靠 TCP:传输控制协议,面向连接的,可靠的,基…...

PyTorch学习笔记(十七)——完整的模型验证(测试,demo)套路
完整代码: import torch import torchvision from PIL import Image from torch import nnimage_path "../imgs/dog.png" image Image.open(image_path) print(image)# 因为png格式是四个通道,除了RGB三通道外,还有一个透明度通…...

WPF开篇
一、为什么要学习WPF 大环境不好,公司要求逐年提高,既要会后端又要会客户端WPF相对于WinForm来说用户界面效果更好,图像更加立体化也是给自己增加一项技能,谨记一句话,技多不压身;多一份技能就多一份竞争力…...

linux 压缩解压缩
压缩解压缩 linux中压缩和解压文件也是很常见的 zip格式 zip格式的压缩包在windows很常见,linux中也有zip格式的压缩包 #压缩#zip [选项] 压缩包名 文件(多个文件空格隔开)zip 1.zip 123.txt 456.txt zip -r 2.zip /home/user1 ---------------------- -r 压缩目录 …...
centos9 mysql8修改数据库的存储路径
一、环境 系统:CentOS Stream release 9 mysql版本:mysql Ver 8.0.34 for Linux on x86_64 (MySQL Community Server - GPL) 二、修改mysql的数据库,存储路径 查看目录数据存储的位置 cat /etc/my.cnf操作 1、新建存放的目录,…...

【C++】<Windows编程中消息即事件的处理>
目录 一、注册窗口类,指定消息处理函数,捕获消息并发给处理函数 二、消息处理函数 三、通用窗口消息 四、其他消息 1.滚动条消息 2.按钮控件消息 3.按钮控件通知消息 4.按键消息 5.系统菜单等消息 6.组合框控件消息 7.组合框控件通知消息 8.列…...

数据库SQL语句使用
-- 查询所有数据库 show databases; -- 创建数据库,数据库名为mydatabase create database mydatabase; -- 如果没有名为 mydatabase的数据库则创建,有就不创建 create database if not exists mydatabase; -- 如果没有名为 mydatabase的数据库则创建…...
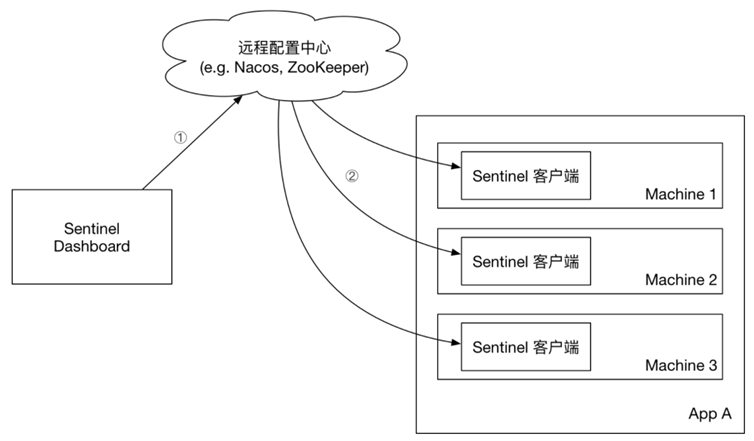
从零开始 Spring Cloud 12:Sentinel
从零开始 Spring Cloud 12:Sentinel 1.初识 Sentinel 1.1雪崩问题 1.1.1什么是雪崩问题 微服务中,服务间调用关系错综复杂,一个微服务往往依赖于多个其它微服务。 如图,如果服务提供者I发生了故障,当前的应用的部分…...

@Resurce和@Autowired的区别
Resource 和 Autowired 是 Java 中常用的两个注解,用于自动装配依赖对象。它们的主要区别如下: 来源不同: Resource 是 Java EE 提供的注解,属于 J2EE 的一部分,它由 JSR-250 规范定义。 Autowired 是 Spring 框架提供…...

ResNet简介
ResNet (Residual Network) 此网络于2015年,国人何先生提出,用于解决随着深度学习的层数加深造成的网络退化现象和梯度消失、梯度爆炸。 问题1 退化现象 当深度学习的各项指标能够随着训练轮数收敛的情况下,网络的层数增强未能像理论一样&…...
)
了解单例模式,工厂模式(简单易懂)
文章目录 单例模式饿汉模式懒汉模式对比 工厂模式简单工厂模式(Simple Factory Pattern)工厂方法模式(Factory Method Pattern)抽象工厂模式(Abstract Factory Pattern)对比 单例模式 什么是单例ÿ…...

【中危】 Apache NiFi 连接 URL 验证绕过漏洞 (CVE-2023-40037)
漏洞描述 Apache NiFi 是一个开源的数据流处理和自动化工具。 在受影响版本中,由于多个Processors和Controller Services在配置JDBC和JNDI JMS连接时对URL参数过滤不完全。使用startsWith方法过滤用户输入URL,导致过滤可以被绕过。攻击者可以通过构造特…...
【Git版本控制工具使用---讲解一】
Git版本控制工具使用 安装设置用户名签名和邮箱Git常用的命令 初始化本地库查看本地状态Git 命令添加暂存区提交本地库查看版本信息修改文件版本穿梭 安装 首先根据自身电脑的配置选择性的安装是32位的还是64位的Git版本控制工具 我这边安装的是64位的 以下是我安装的时候的过…...

NLP | 基于LLMs的文本分类任务
比赛链接:讯飞开放平台 来源:DataWhale AI夏令营3(NLP) Roberta-base(BERT的改进) ①Roberta在预训练的阶段中没有对下一句话进行预测(NSP) ②采用了动态掩码 ③使用字符级和词级…...
攻防世界-base÷4
原题 解题思路 base644,莫不是base16,base16解码网站: 千千秀字...
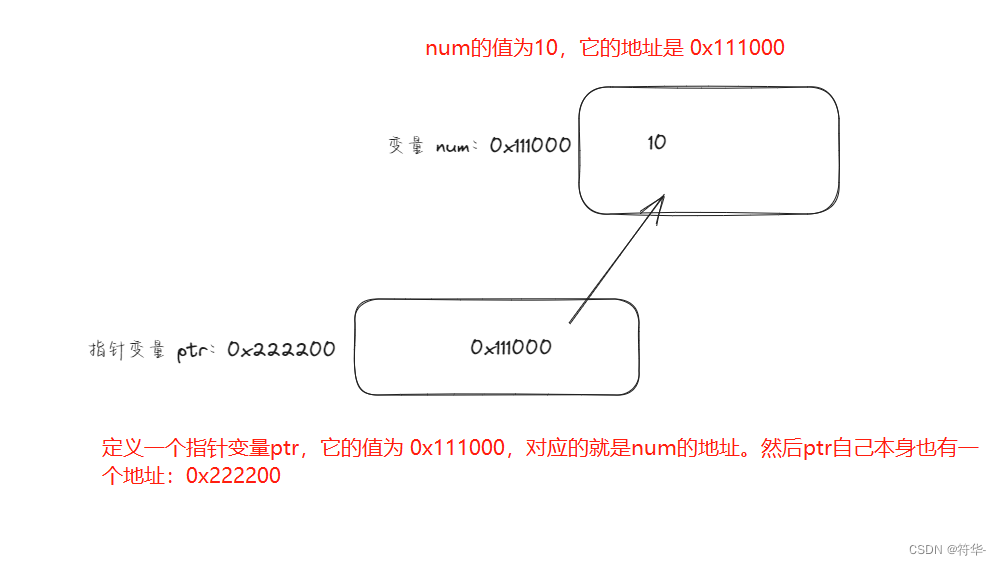
【Java转Go】快速上手学习笔记(三)之基础篇二
【Java转Go】快速上手学习笔记(二)之基础篇一 了解了基本语法、基本数据类型这些使用,接下来我们来讲数组、切片、值传递、引用传递、指针类型、函数、map、结构体。 目录 数组和切片值传递、引用传递指针类型defer延迟执行函数map结构体匿名…...

【vue 引入pinia与pinia的详细使用】
vue引入pinia与使用 安装引入使用定义 store在组件中使用 store在插件中使用 store配置 store 总结 Pinia 是一个用于 Vue 3 的状态管理库,其设计目标是提供一个简单、一致的 API 和强类型支持。下面介绍如何引入 Pinia 并使用它。 安装 npm install pinia引入 在…...

USACO18DEC Fine Dining G
P5122 [USACO18DEC] Fine Dining G 题目大意 有一个由 n n n个点 m m m条边构成的无向连通图,这 n n n个点的编号为 1 1 1到 n n n。前 n − 1 n-1 n−1个点上都有一头奶牛,这些奶牛都要前往 n n n号点。第 i i i条边连接 a i a_i ai和 b i b_i bi…...

fckeditor编辑器的两种使用方法
需要的资源包我放我资源里了,不要积分 https://download.csdn.net/download/wybshyy/88245895 首先把FredCK.FCKeditorV2.dll添加到引用 具体方法如下,一个是客户端版本,一个是服务器端版本 客户端版本: <% Page Language…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
