E - Excellent Views
Problem - E - Codeforces
问题描述:数组H大小都不相同。从i到j是可行的,当且仅当
不存在 k ,使 ∣ i − k ∣ ≤ ∣ i − j ∣ , H k > H j 不存在k,使 \\ |i - k| \leq |i - j|, \quad H_k > H_j 不存在k,使∣i−k∣≤∣i−j∣,Hk>Hj
暴力 O(n * n),从当前点向两边进行扩散。
void solve() {int n;cin>>n;for(int i = 1; i <= n; ++i) cin>>a[i];for(int i = 1; i <= n; ++i) {int ma = -INF;int cnt = 0;int len = max(i - 1, n - i);for(int j = 0; j <= len; ++j) {int lvidx = i - j, rvidx = i + j;if(lvidx < 1) {ma = max({ma, a[rvidx]});if(a[rvidx] >= ma) cnt++;} else {ma = max({ma, a[lvidx], a[rvidx]});if(a[lvidx] >= ma) cnt++;if(a[rvidx] >= ma) cnt++;}}cout<<cnt - 2<<" ";}
}
优化:单调栈,对于i算出到左边和到右边第一个大于下标为i的元素值得长度或下标,用差分对半记录即可。
代码:
#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <queue>
#include <ctime>
#include <random>
#include <sstream>
#include <stack>
#include <numeric>
#include <stdio.h>
#include <functional>
#include <bitset>
#include <algorithm>
using namespace std;// #define Multiple_groups_of_examples
#define IOS std::cout.tie(0);std::cin.tie(0)->sync_with_stdio(false);
#define dbgnb(a) std::cout << #a << " = " << a << '\n';
#define dbgtt cout<<" !!!test!!! "<<endl;
#define rep(i,x,n) for(int i = x; i <= n; i++)#define all(x) (x).begin(),(x).end()
#define pb push_back
#define vf first
#define vs secondtypedef long long LL;
typedef pair<int,int> PII;
/*** https://codeforces.com/gym/103185/problem/E* 题意:对每一个i找到满足条件的j, 其中条件为:不存在k, 使 abs(i - k) <= abs(i - j) && Hj < Hk 成立* 解法:std:https://github.com/Diego1149/ICPC-Latam-2020 (好像是用线段树写的* other:https://blog.csdn.net/m0_53807008/article/details/119065842* * 思路:单调栈* 两次单调栈。这里为了简单,假设 1 <= i < j <= n* 第一次找 对于j来说,从i到j中满足条件的元素(这里j是题意中的i。* 第二次找,对于i来说,从i到j中满足条件的元素(这里i就是题意中的i。* e.g. 下标: ... 符合条件的 i 符合条件的 ...* 对于第一次来说:* 比a[i]小的最大元素(记为A)下标找到,将比a[i]小的最大元素下标对应得pre数组赋值 i - 1,表示,最后一个小于A的下标位置。* 对于那个最大元素下标(记为idx),使 idx 对应的元素可以worth的长度为 [idx, i - 1]的一半。* 记录用差分记录即可。* 第二次,倒着来一边,同第一次。
*/
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 21;
int a[N];
int pre[N], suf[N];
int lef[N], rig[N];
void inpfile();
void solve() {int n; cin>>n;for(int i = 1; i <= n; ++i) cin>>a[i];a[n+1] = INF; // 让 n + 1 等于inf, 0 等于inf,因为要让所以的都出栈stack<int> sk;// 考虑a[i]对左边的贡献sk.push(1);for(int i = 2; i <= n+1; ++i) {// 如果当前 H 大于 上一个H,将上一个H对应的下标进行记录while(sk.size() && a[i] > a[ sk.top()]) {pre[ sk.top()] = i - 1; // 将i - 1进行赋值,表示到i - 1 ,大于的条件一直是成立的sk.pop();}sk.push(i);}for(int i = 1; i <= n; ++i) {lef[i+1]++; // 将i + 1 先进行++,表示有一个贡献if(pre[i] != n) // 如果等于n,表示,恒成立,不用--,// 否则,只能到达 (i + pre[i]) / 2 的下标,利用差分 就是 [ r + 1]--lef[ (i + pre[i]) / 2 + 1]--;}// 考虑a[i]对右边的贡献// 思路及代码同上sk.push(n);a[0] = INF;for(int i = n - 1; i >= 0; --i) {while(sk.size() && a[i] > a[ sk.top()]) {suf[ sk.top()] = i + 1;sk.pop();}sk.push(i);}for(int i = 1; i <= n; ++i) {rig[i-1]++;if(suf[i] != 1)rig[ (i + suf[i] + 1) / 2 - 1]--;}// 差分前缀和for(int i = 1; i <= n; ++i) lef[i] += lef[i-1];for(int i = n; i >= 1; --i) rig[i] += rig[i+1];for(int i = 1; i <= n; ++i) cout<<lef[i] + rig[i]<<" ";
}
int main()
{#ifdef Multiple_groups_of_examplesint T; cin>>T;while(T--)#endifsolve();return 0;
}
void inpfile() {#define mytest#ifdef mytestfreopen("ANSWER.txt", "w",stdout);#endif
}
Gym - 103185E E - Excellent Views_流锡的博客-CSDN博客
相关文章:

E - Excellent Views
Problem - E - Codeforces 问题描述:数组H大小都不相同。从i到j是可行的,当且仅当 不存在 k ,使 ∣ i − k ∣ ≤ ∣ i − j ∣ , H k > H j 不存在k,使 \\ |i - k| \leq |i - j|, \quad H_k > H_j 不存在k,使…...

WiFi天线和NB-IoT天线不通用
表面看起来完全一样。但是把WiFi天线插到NB-IoT设备后,信号弱了很多。还导致设备反复重启...
IoT DC3 是一个基于 Spring Cloud 的开源的、分布式的物联网(IoT)平台本地部署步骤
dc3 windows 本地搭建步骤: 必要软件环境 进入原网页# 务必保证至少需要给 docker 分配:1 核 CPU 以及 4G 以上的运行内存! JDK : 推荐使用 Oracle JDK 1.8 或者 OpenJDK8,理论来说其他版本也行; Maven : 推荐…...
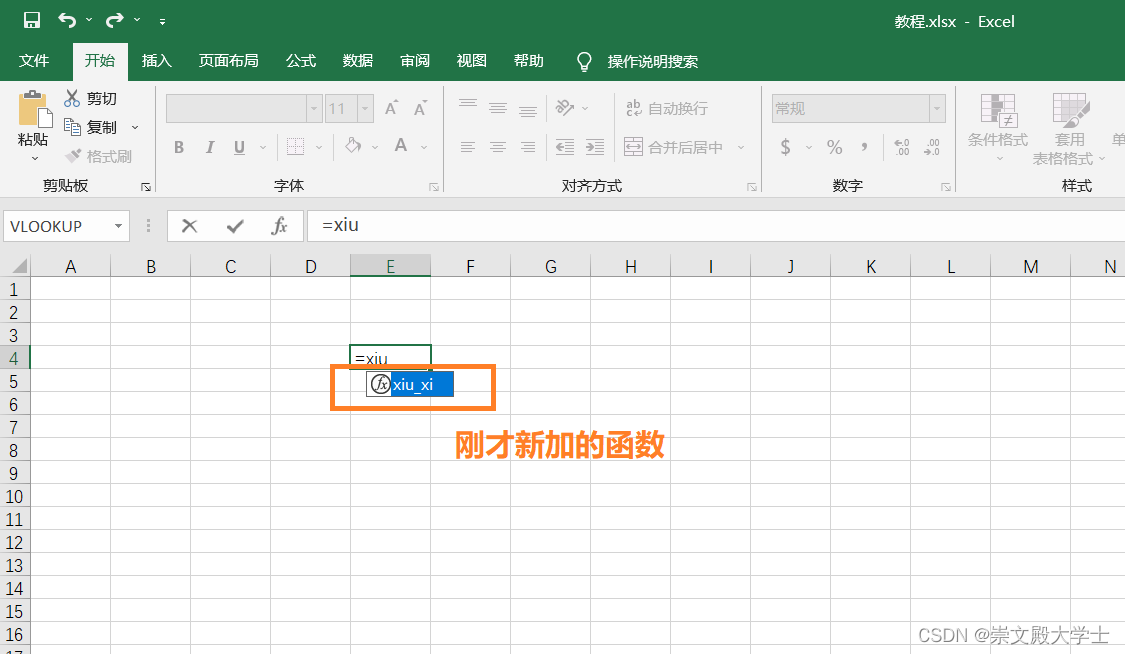
VBA Excel自定义函数的使用 简单的语法
一个简单的教程,实现VBA自定义函数。 新建模块 复制后面的代码放进来 函数的入口参数不定义,则认为是一块区域; 反之,如FindChar1 As String,则认为是输入的单值。 循环和分支如下例子,VB比较接近自然语…...

字节跳动 从需求到上线全流程 软件工程流程 需求评估 MVP
走进后端开发流程 整个课程会带大家先从理论出发,思考为什么有流程 大家以后工作的团队可能不一样,那么不同的团队也会有不同的流程,这背后的逻辑是什么 然后会带大家按照走一遍从需求到上线的全流程,告诉大家在流程的每个阶段&am…...

线性代数-矩阵的本质
线性代数-矩阵的本质 线性代数-矩阵的本质...
React基础入门之虚拟Dom
React官方文档:https://react.docschina.org/ 说明 重要提示:本系列文章基础篇总结自尚硅谷课程,且采用类式写法!!最新的函数式组件写法见高级篇。 本系列文档旨在帮助vue同学更快速的学习react,如果你很…...
C++基础Ⅰ编译、链接
目录儿 1 C是如何工作的1.1 预处理语句1.2 include1.3 main()1.4 编译单独编译项目编译 1.5 链接 2 定义和调用函数3 编译器如何工作3.1 编译3.1.1 引入头文件系统头文件自定义头文件 3.1.2 自定义类型3.1.3 条件判断拓展: 汇编 3.2 链接3.2.1 起始函数3.2.2 被调用的函数 3.3 …...

VMware和ubuntu配置Hadoop环境
目录 一、获取VMware安装包 1、官网获取 1)首先先进入官网,官网首页是下面这样: 2)接着点击产品选项 3)进入后点击查看所有产品,然后在右上角选择排序方式为Z到A,然后向下滑动找到Workstation…...
uview2.0自定义tabbar
tabbar组件 <template><u-tabbar :value"tab" change"changeTab" :fixed"true" :border"true" :placeholder"true":safeAreaInsetBottom"true"><u-tabbar-item text"消息" icon"c…...
Star History 月度开源精选|Llama 2 及周边生态特辑
7 月 18 日,Meta 发布了 Llama,大语言模型 Llama 1 的进阶版,可以自由免费用于研究和商业,支持私有化部署。 所以本期 Star History 的主题是:帮助你快速把 Llama 2 在自己机器上跑起来的开源工具,无论你的…...

修改电脑上路由表使笔记本默认走无线
如果笔记本上即连接了有线,也连接了无线,默认电脑会走有线的,通过route print命令查看路由表就可以看出来,因为无线的“metric”跳数要比有线的高 解决方法: 如果想实现让默认走无线,就需要修改自己电脑的…...

Spring Cache的介绍以及怎么使用(redis)
Spring Cache 文章目录 Spring Cache1、Spring Cache介绍2、Spring Cache常用注解2.1、EnableCaching注解2.2、CachePut注解2.3、CacheEvict注解2.4、Cacheable注解 3、Spring Cache使用方式--redis 1、Spring Cache介绍 Spring Cache是一个框架,实现了基于注解的缓…...

软考高级系统架构设计师系列论文六十九:论信息系统的安全风险评估
一、信息系统相关知识点 软考高级信息系统项目管理师系列之四十三:信息系统安全管理软考高级系统架构设计师:系统安全分析与设计...
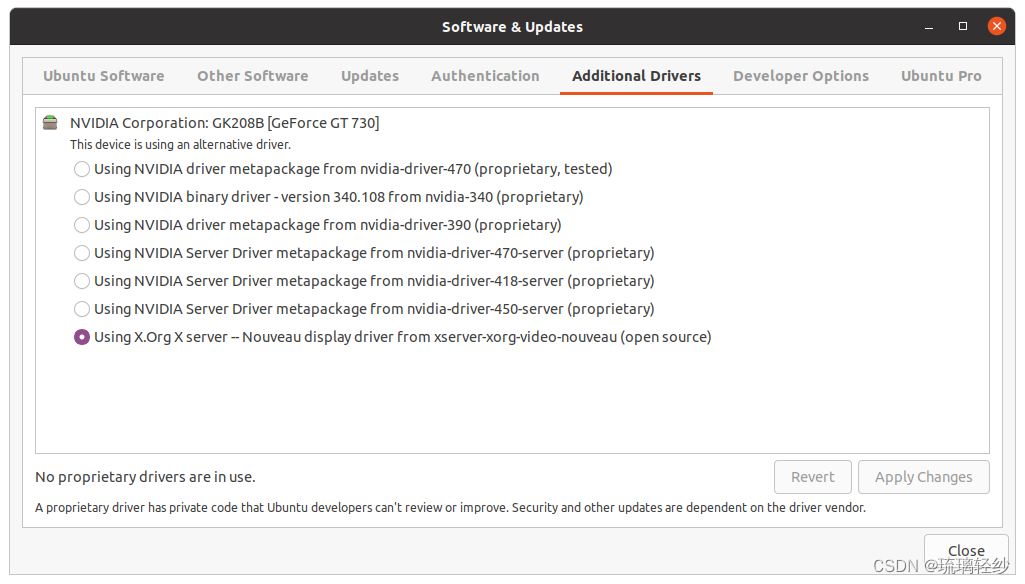
Ubuntu系统安装之后首需要做的事情
Ubuntu系统的初步环境搭建 1、换源2、显卡3、浏览器4、输入法5、终端6、ROS7、VSCode8、设置时间与win一致9、 TimeShift10、 Anaconda(考虑装不装) 1、换源 点开Software&&Update,找到Ubuntu Software中的Download from,…...

Qt——QPushButton控件的常见属性、方法和信号
Qt中QPushButton控件的常见属性、方法和信号 一、QPushButton控件常见属性 一、QPushButton控件常见方法 一、QPushButton控件常见信号 一、QPushButton控件常见属性(Properties) 1. text: 描述:按钮上显示的文本。 用法: butto…...
5.5 基于ISOLAR-A的系统级设计与配置方法(上))
AUTOSAR规范与ECU软件开发(实践篇)5.5 基于ISOLAR-A的系统级设计与配置方法(上)
目录 前言 1 系统配置输入文件创建与导入 2、 Composition SWC建立 前言 如前所述, AUTOSAR支持整车级别的软件架构设计, 开发人员可以进行整车级别的软件组件定义, 再将这些软件组件分配到各个ECU中, 这就是AUTOSAR系统级设计需要完成的主要任务。 下面结合AUTOSAR方法论…...
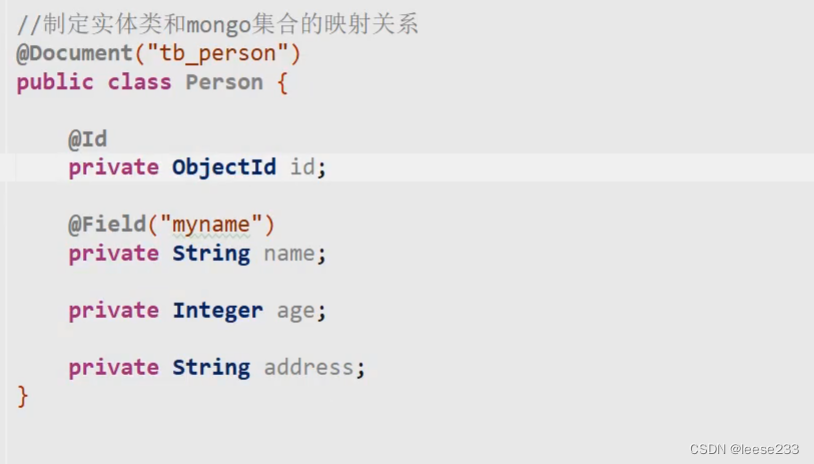
mongoDB的CRUD
...
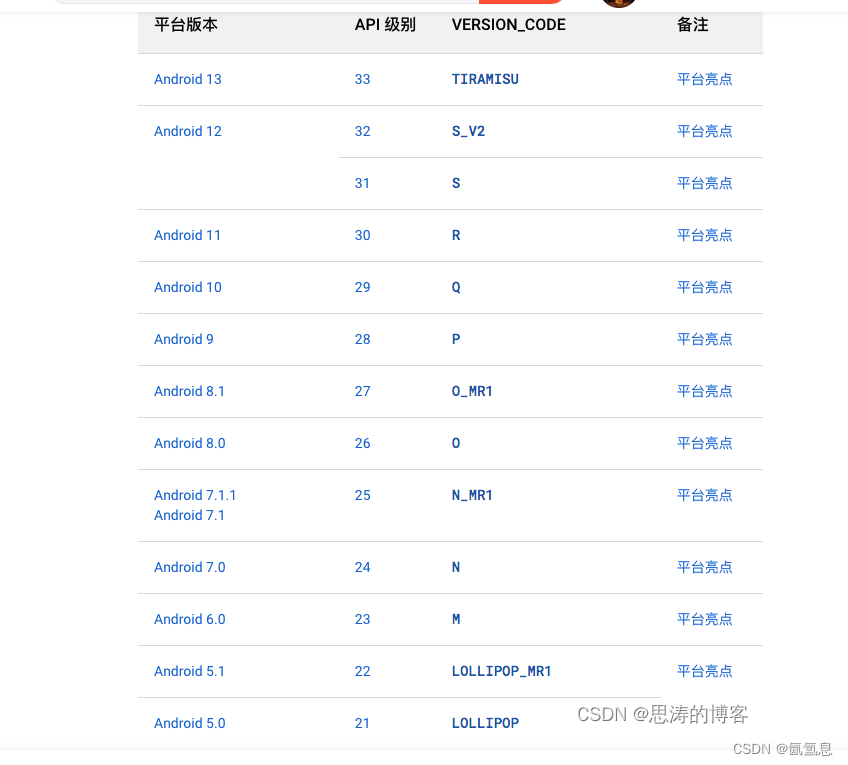
flutter TARGET_SDK_VERSION和android 13
config.gradle ext{SDK_VERSION 33MIN_SDK_VERSION 23TARGET_SDK_VERSION 33COMPILE_SDK_VERSION SDK_VERSIONBUILD_TOOL_VERSION "33.0.0"//兼容库版本SUPPORT_LIB_VERSION "33.0.0"}app/build.gradle里面的 defaultConfig {// TODO: Specify your…...

大数据Flink(六十六):Flink的重要概念和小结
文章目录 Flink的重要概念和小结 一、数据流图(Dataflow Graph)...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
