NOIP真题答案 过河 数的划分
过河
题目描述
在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点:0,1,⋯ ,L0,1,\cdots,L0,1,⋯,L(其中 LLL 是桥的长度)。坐标为 000 的点表示桥的起点,坐标为 LLL 的点表示桥的终点。青蛙从桥的起点开始,不停的向终点方向跳跃。一次跳跃的距离是 SSS 到 TTT 之间的任意正整数(包括 S,TS,TS,T)。当青蛙跳到或跳过坐标为 LLL 的点时,就算青蛙已经跳出了独木桥。
题目给出独木桥的长度 LLL,青蛙跳跃的距离范围 S,TS,TS,T,桥上石子的位置。你的任务是确定青蛙要想过河,最少需要踩到的石子数。
输入输出格式
第一行有 111 个正整数 L(1≤L≤109)L(1\le L\le 10^9)L(1≤L≤109),表示独木桥的长度。
第二行有 333 个正整数 S,T,MS,T,MS,T,M,分别表示青蛙一次跳跃的最小距离,最大距离及桥上石子的个数,其中 1≤S≤T≤101\le S\le T\le101≤S≤T≤10,1≤M≤1001\le M\le1001≤M≤100。
第三行有 MMM 个不同的正整数分别表示这 MMM 个石子在数轴上的位置(数据保证桥的起点和终点处没有石子)。所有相邻的整数之间用一个空格隔开。
输出格式
一个整数,表示青蛙过河最少需要踩到的石子数。
输入输出样例
说明
对于30%的数据,L≤104L \le 10^4L≤104;
对于全部的数据,L≤109L \le 10^9L≤109。
**【题目来源】**
NOIP 2005 提高组第二题
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 200 + 10;
int n, na, nb, a[MAXN], b[MAXN], cnta, cntb;
int vs[5][5] = {{0,0,1,1,0},{1,0,0,1,0},{0,1,0,0,1},{0,0,1,0,1},{1,1,0,0,0}}; //得分表的处理
int main()
{cin >> n >> na >> nb;for(int i = 0; i < na; i++) cin >> a[i];for(int i = 0; i < nb; i++) cin >> b[i];for(int i = 0; i < n; i++){cnta += vs[a[i % na]][b[i % nb]]; //周期循环 cntb += vs[b[i % nb]][a[i % na]];}cout << cnta << " " << cntb << endl;return 0;
}
数的划分
Description
将整数 nnn 分成 kkk 份,且每份不能为空,任意两个方案不相同(不考虑顺序)。
例如:n=7n=7n=7,k=3k=3k=3,下面三种分法被认为是相同的。
1,1,51,1,51,1,5;
1,5,11,5,11,5,1;
5,1,15,1,15,1,1.
问有多少种不同的分法。
Input
n,kn,kn,k (6≤n≤2006 \le n \le 2006≤n≤200,2≤k≤62 \le k \le 62≤k≤6)
Output
111 个整数,即不同的分法。
Samples
</div></div></div>
</div>
#include<bits/stdc++.h>
using namespace std;
long long q,w,e,r,t,y,u,o,p,s,d,f,g,h,j,l,z,x,c,v,n,m,i;
long long k;
long long a[10000][10000],b[10000];
int main()
{cin>>n>>k;for(i=1;i<=n;i++){a[1][i]=1;}for(l=1;l<=n;l++){for(i=2;i<=n;i++){ for(j=i;j<=n;j++){ a[i][j]=a[i-1][j-1]+a[i][j-i];}}}cout<<a[k][n];return 0;
}
相关文章:

NOIP真题答案 过河 数的划分
过河 题目描述 在河上有一座独木桥,一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子,青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数,我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点…...
图为科技-边缘计算在智慧医疗领域的作用
边缘计算在智慧医疗领域的作用 随着科技的进步,智慧医疗已成为医疗行业的重要发展趋势。边缘计算作为新兴技术,在智慧医疗领域发挥着越来越重要的作用。本文将介绍边缘计算在智慧医疗领域的应用及其优势,并探讨未来发展方向。 一、边缘计算…...
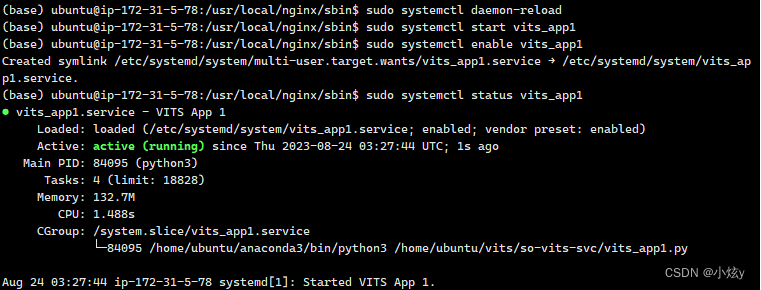
Linux配置nginx反向代理
在云服务器上部署高并发的服务,使用Nginx作为反向代理是一种常见的做法,可以实现流量分发、负载均衡,同时提升系统的可靠性和性能。 步骤概览: 安装Nginx: 确保服务器已安装Nginx。若未安装,可使用适用于你…...

随便记录记录
统一整理一下各种 pandas读csv import pandas as pd ## 默认会将第一行作为列 df pd.read_csv(path_to_your_file.csv) ## 传递 headerNone 参数来告诉 Pandas 不要将第一行 df pd.read_csv(path_to_your_file.csv, headerNone) ## 使用多种选项来处理数据,如指…...

UbuntuDDE 23.04发布,体验DeepinV23的一个新选择
UbuntuDDE 23.04发布,体验DeepinV23的一个新选择 昨晚网上搜索了一圈,无意看到邮箱一条新闻,UbuntuDDE 23.04发布了 因为前几天刚用虚拟机安装过,所以麻溜的从网站下载了ISO文件,安装上看看。本来没多想,…...
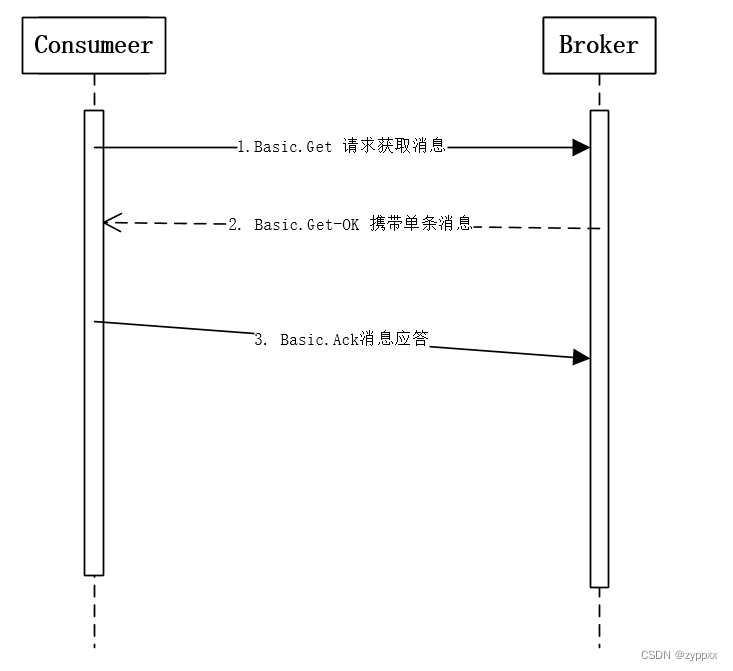
RabbitMQ 消费者
RabbitMQ的消费模式分两种:推模式和拉模式,推模式采用Basic.Consume进行消费,拉模式则是调用Basic.Get进行消费。 消费者通过订阅队列从RabbitMQ中获取消息进行消费,为避免消息丢失可采用消费确认机制 消费者 拉模式拉模式的实…...

软件测试面试真题 | 什么是PO设计模式?
面试官问:UI自动化测试中有使用过设计模式吗?了解什么是PO设计模式吗? 考察点 《page object 设计模式》:PageObject设计模式的设计思想、设计原则 《web自动化测试实战》:结合PageObject在真实项目中的实践与应用情…...

GB2312转UTF-8部分中文乱码
现象 最近写了个txt导入,客户反馈有时候导入的数据,会出现个别中文乱码的现象,但是我之前已经做过编码转换处理了,统一转成了UTF-8。 比如“鞠婧祎”,导入进来是这样: 排查思路 首先看了一下这个文本的编码格式&am…...
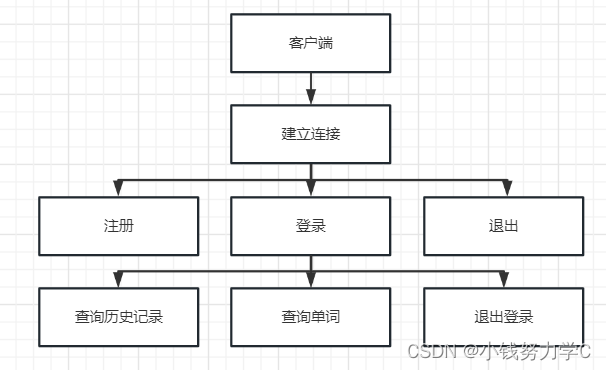
项目——电子词典(客户端、服务器交互,字典导入,单词查询)
一、项目要求 登录注册功能,不能重复登录,重复注册单词查询功能历史记录功能,存储单词,意思,以及查询时间基于TCP,支持多客户端连接采用数据库保存用户信息与历史记录将dict.txt的数据导入到数据库中保存。…...
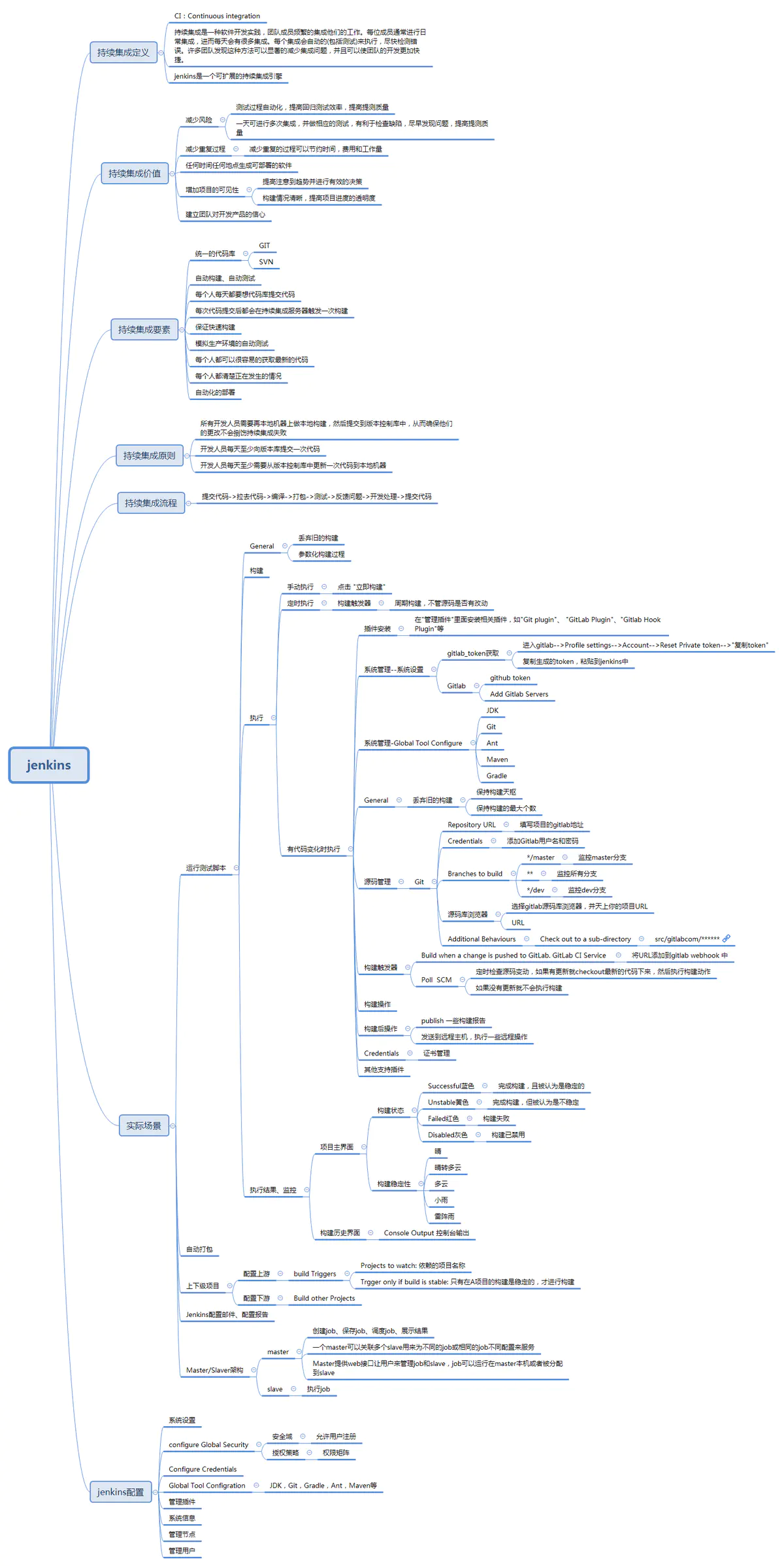
jenkins 是什么?
一、jenkins 是什么? Jenkins是一个开源的、提供友好操作界面的持续集成(CI)工具,起源于Hudson,主要用于持续、自动的构建/测试软件项目、监控外部任务的运行。Jenkins用Java语言编写,可在Tomcat等流行的servlet容器中运行&#…...

无涯教程-PHP - sql_regcase()函数
sql_regcase() - 语法 string sql_regcase (string string) 可以将sql_regcase()函数视为实用程序函数,它将输入参数字符串中的每个字符转换为包含两个字符的带括号的表达式。 sql_regcase() - 返回值 返回带括号的表达式字符串以及转换后的字符。 sql_regcase…...

cesium 实现鼠标中键拖动地图
cesium默认左键拖动地图,中键旋转,再绘图时带来诸多不便。所以改成鼠标中键按下拖动地图,鼠标左键选点。代码如下:【感谢chatGPT】 //改为中建拖动// 假设 viewer 是你的 Cesium Viewer 实例const cameraController viewer.scene…...

低压风机单片机方案
低压风机通常由电机、转子、机壳、进气管、出气管、齿轮和减速机等组成。电机带动转子旋转,旋转的转子带动齿轮和减速机转动,进而形成空气被吸入转子内部,通过旋转而产生的离心力把气体压缩,并将气体排出。 低压风机方案的主控型…...

R语言06-R语言的基本运算
概念 R语言支持多种基本运算,包括算术运算、逻辑运算、比较运算和向量化运算等。 代码示意 逻辑运算 a <- TRUE b <- FALSElogical_and <- a & b # 逻辑与 logical_or <- a | b # 逻辑或 logical_not <- !a # 逻辑非比较运算 x <…...

Docker容器:docker-compose管理创建LNMP服务并运行Wordpress网站平台
文章目录 一.项目环境1. 环境描述2.项目需求 二.部署过程1.安装Docker2.安装Docker加速器3.Docker-Compose安装部署4.准备依赖文件、配置nginx5.配置mysql6.配置php7.编写docker-compose.yml8.验证 三.容器快照,然后将Docker镜像打包成tar包备…...

实业兴国 守护种源 —— 白露木實®农业的活力之风
高科技领域,芯片是生命线;而在农业领域,种源与芯片在高科技领域的重要性是相同的。保护、发展、培育我国的种质资源,是中国农业发展至为关键的一环。但是,因为思想、观念、认识、技术等方面的原因,让我们错…...

Web3.0
一、Web3.0是什么 Web3.0(有时称为“分布式Web”或“去中心化Web”)是对互联网的下一代演进的概念。它代表了一种更加分散、去中心化和用户掌控的互联网模式,与传统的Web2.0模型有很大不同。 以下是Web3.0的一些关键特征和概念:…...

精密图纸被窃,知名手表品牌Seiko遭BlackCat勒索软件攻击
据BleepingComputer消息,日本著名手表制造商Seiko在7月末遭到了网络攻击,8月21日,BlackCat(又名ALPHV)勒索软件组织在其网站上宣布对这起攻击事件负责。 8 月 10 日,Seiko发布了一份数据泄露通知࿰…...
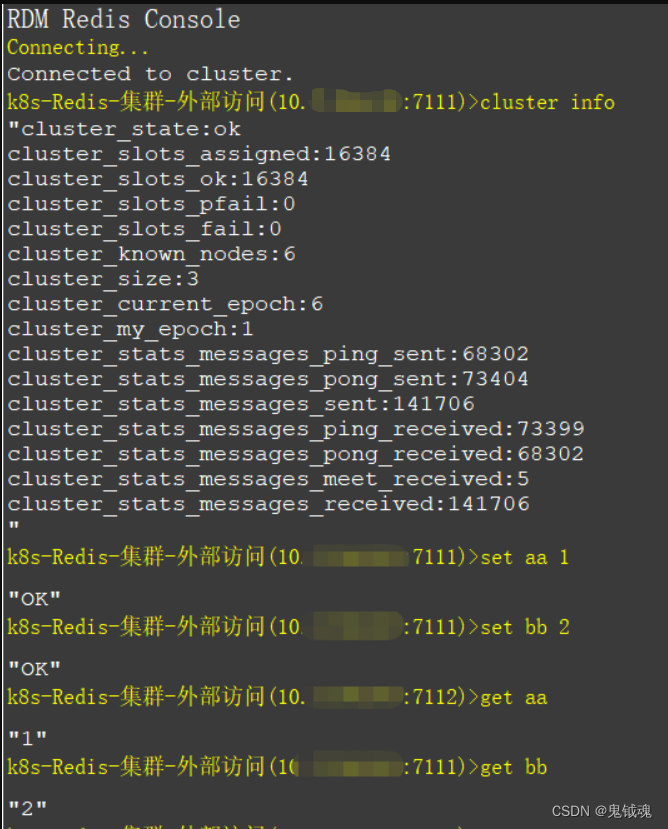
K8S如何部署Redis(单机、集群)
在今天的讨论中,我们将深入研究如何将Redis数据库迁移到云端,以便更好地利用云计算的优势提高数据管理的灵活性。 Redis(Remote Dictionary Server)是一个开源的、基于内存的数据结构存储系统,它可以用作数据库、缓存和消息代理。Redis支持多…...

Flask狼书笔记 | 03_模板
文章目录 3 模板3.1 模板基本使用3.2 模板结构组织3.3 模板进阶 3 模板 模板(template):包含固定内容和动态部分的可重用文件。Jinja2模板引擎可用于任何纯文本文件。 3.1 模板基本使用 HTML实体:https://dev.w3.org/html5/htm…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...
