【线性DP】模型总结(terse版)
【线性DP】模型总结
最长上升子序列
DP法
dp[i]表示以i结尾的最长上升子序列的长度。
对于每个i,遍历j=1~i-1,若a[j] < a[i], 则dp[i] = max(dp[i], dp[j] + 1);
二分法
可以优化时间复杂度。
dp[]数组用来存储当前最长上升子序列。
若dp[]数组的最末尾的值小于当前原序列的值,则将这个值加入dp[]数组末尾。
否则,使用Lower_bound找到dp[]数组中第一个大于该值的元素,替换。
如果需要输出序列:定义s[]数组,记录下标,随dp[]数组更新。
最长公共子序列
定义dp[] []二维数组,表示a串以i结尾,b串以j结尾的最长公共子序列。
枚举i = 1 ~ a.size(), j = 1 ~ b.size().
若a[i - 1] == b[j - 1], dp[i] [j] = dp[i - 1] [j - 1] + 1;
否则 dp[i] [j] = max(dp[i - 1] [j], dp[i] [j - 1])。
最大子矩阵
首先遍历len=1~n,再将i从1遍历,确定j的值,得出一个len行n列的值,每一列对应相加,得到1行n列的序列,再求线性最大子段和。
得到的最大值就是Len行(从i到j)的最大子矩阵的值。
每次求都不断更新ans = max(ans, dp[i])。
最大正方形
给出一个01矩阵,求都是1的最大正方形的边长
dp[i] [j] 表示以x=i,y=j为右下角的最大正方形。 若a[i - 1] [j]、a[i] [j - 1]、a[i - 1] [ j - 1]均为1,则正方形的边长可以加一,即dp[i] [j] + 1。
否则,dp[i] [j] = min(dp[i - 1] [j]、dp[i] [j - 1]、dp[i - 1] [ j - 1])
题目:最大子矩阵
代码:AC代码
最大子段和
线性
定义dp[]一维数组,dp[i]表示以i结尾的最大字段和的值。
有两种情况:
1.独自成串:dp[i] = a[i];
2.与前一个元素连成串:dp[i] = dp[i - 1] + a[i];
合并得:dp[i] = max(dp[i - 1] + a[i], a[i])。
答案是dp[1~n]中最大值。
环形
依照上述方法,求出序列和、最大字段和、最小字段和。
答案 = max(和 - 最小字段和, 最大字段和)。
子集和问题
定义dp[] []bool类二维数组,dp[i] [j] 表示前i个数存在一个子集和等于j,答案就是dp[n] [M]。
s[]数组记录集合中元素。
若s[i] > j,则不能放入, dp[i] [j] = dp[i - 1] [j]。
否则, 放不放皆可,dp[i] [j] = (dp[i - 1] [j] || dp[i - 1] [j - s[i]])。
行走问题
类似于爬楼梯。
给出目标阶梯数和每步最多爬几层。
对于每个dp[i]表示走到第i层的步数总数,每次遍历j=i - k~i - 1,dp[i] += dp[j]。
答案就是dp[n]。
相关文章:
)
【线性DP】模型总结(terse版)
【线性DP】模型总结 最长上升子序列 DP法 dp[i]表示以i结尾的最长上升子序列的长度。 对于每个i,遍历j1~i-1,若a[j] < a[i], 则dp[i] max(dp[i], dp[j] 1); 二分法 可以优化时间复杂度。 dp[]数组用来存储当前最长上升子序列。 若dp[]数…...

conda 常用命令
conda 常用命令 一、创建环境二、删除环境三、环境重命名四 、查看环境列表五、进入某个虚拟环境六、退出当前环境七、查看当前虚拟环境下的所有安装包八、安装或卸载包(进入虚拟环境之后)九、分享虚拟环境十、源服务器管理十一、升级十二、卸载十三、卸载十四、pip…...

前端面试:【异步编程】Callback、Promise和Async/Await
嗨,亲爱的JavaScript探险家!在JavaScript开发的旅程中,你会经常遇到异步编程的需求。为了处理异步操作,JavaScript提供了多种机制,包括Callbacks、Promises和Async/Await。本文将深入介绍这些机制,让你能够…...
:Pandas的基础应用详解)
大数据(四):Pandas的基础应用详解
专栏介绍 结合自身经验和内部资料总结的Python教程,每天3-5章,最短1个月就能全方位的完成Python的学习并进行实战开发,学完了定能成为大佬!加油吧!卷起来! 全部文章请访问专栏:《Python全栈教…...

计算机网络第3章(数据链路层)
计算机网络第3章(数据链路层) 3.1 数据链路层概述3.1.1 概述3.1.2 数据链路层使用的信道3.1.3 三个重要问题 3.2 封装成帧3.2.1 介绍3.2.2 透明传输3.2.3 总结 3.3 差错检测3.3.1 介绍3.3.2 奇偶校验3.3.3 循环冗余校验CRC(Cyclic Redundancy Check)3.3.…...

stm32之4.时钟体系
3.时钟体系(给单片机提供一个非常稳定的频率信号) ①可以使用三种不同的时钟源来驱动系统时钟(SYSCLK),CPU运行的频率为168MHZ; HSI(RC振荡器时钟,也就是高速内部时钟,一般来说很少用,因为精度…...
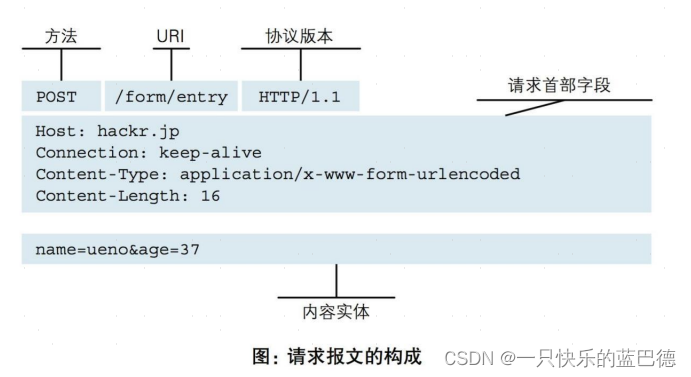
RPC和HTTP协议
RPC 全称(Remote Procedure Call),它是一种针对跨进程或者跨网络节点的应用之间的远程过程调用协议。 它的核心目标是,让开发人员在进行远程方法调用的时候,就像调用本地方法一样,不需要额外为了完成这个交…...

BUGFix:onnx -> TensorRT转换过程失败
先附上相关的onnx2trt的部分代码: def onnx2trt(onnx_path):logger trt.Logger(trt.Logger.ERROR)builder trt.Builder(logger)network builder.create_network(1 << int(trt.NetworkDefinitionCreationFlag.EXPLICIT_BATCH))parser trt.OnnxParser(netw…...

FFMPEG小白常用命令行
序列帧转H264视频 ffmpeg -r 60 -f image2 -s 1920x1080 -i fram%d.jpg -vcodec libx264 -crf 25 -pix_fmt yuv420p test.mp4 -vcodec h264 .\ffmpeg -r 60 -f image2 -s 1920x1080 -i %04d.jpeg -vcodec h264 test.mp4 %04d 表示用零来填充直到长度为4,i.e 000…...

个性定制还是纯粹简约:探寻界面选择背后的心理宇宙
在数码世界中,我们的界面选择成为了一张架起的桥梁,连接着个性的渴望与效率的追求。当我们面对个性化定制界面和极简版原装界面,我们仿佛站在了一座分岔路口,左右各有一片令人心驰神往的风景。究竟是走向五光十色的个性世界&#…...

【Java 高阶】一文精通 Spring MVC - 转发重定向(四)
👉博主介绍: 博主从事应用安全和大数据领域,有8年研发经验,5年面试官经验,Java技术专家,WEB架构师,阿里云专家博主,华为云云享专家,51CTO 专家博主 ⛪️ 个人社区&#x…...
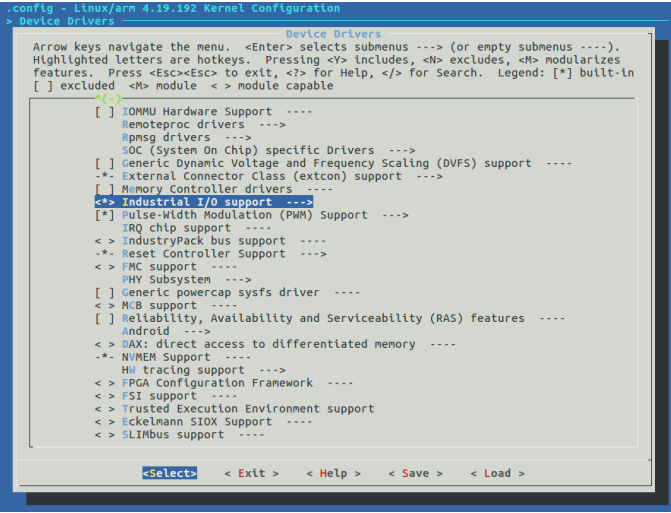
嵌入式Linux开发实操(十):ADC接口开发
#前言 ADC就是模数转换,可以用来接一些模拟量设备,所谓模拟量就是波形不是方波而是各种包络形状的波形的信号,比如电压、电流等电信号或压力、温度、湿度、位移、声音等非电信号,ADC就是将这些信号转换为数字方波信号,以便于信息传递的。 #ADC硬件设计 key按键连接了AD…...
精进语言模型:探索LLM Training微调与奖励模型技术的新途径
大语言模型训练(LLM Training) LLMs Trainer 是一个旨在帮助人们从零开始训练大模型的仓库,该仓库最早参考自 Open-Llama,并在其基础上进行扩充。 有关 LLM 训练流程的更多细节可以参考 【LLM】从零开始训练大模型。 使用仓库之…...

数据采集:selenium 提取 Cookie 自动登陆
写在前面 工作需要,简单整理博文内容涉及 通过 selenium 实现自动登陆理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的&#x…...

[Go版]算法通关村第十三关黄金——数字数学问题之数论问题(最大公约数、素数、埃氏筛、丑数)
目录 题目:辗转相除法(求最大公约数)思路分析:辗转相除法(也叫欧几里得算法)gcd(a,b) gcd(b,a mod b)复杂度:时间复杂度 O ( n l o g ( m a x ) ) O(nlog(max)) O(nlog(max))、空间复杂度 O (…...
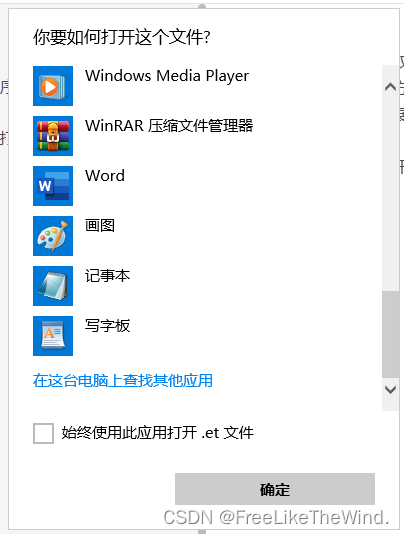
Qt双击某一文件通过自己实现的程序打开,并加载文件显示
双击启动 简述方法一方法二注意 简述 在Windows系统中,双击某类扩展名的文件,通过自己实现的程序打开文件,并正确加载及显示文件。有两种方式可以到达这个目的。 对于系统不知道的扩展名的文件,第一次打开时,需要自行…...

硬件产品的量产问题------硬件工程师在产线关注什么
前言: 产品开发测试无误,但量产缺遇到很多不良甚至DOA问题。 硬件开发过程中如何确保产线的治具、生产及硬件工程师在产线需要关注一些什么。 坚信:好的产品是要可以做出来的。 1、禁忌: 禁忌热插拔;禁忌测试不防呆…...
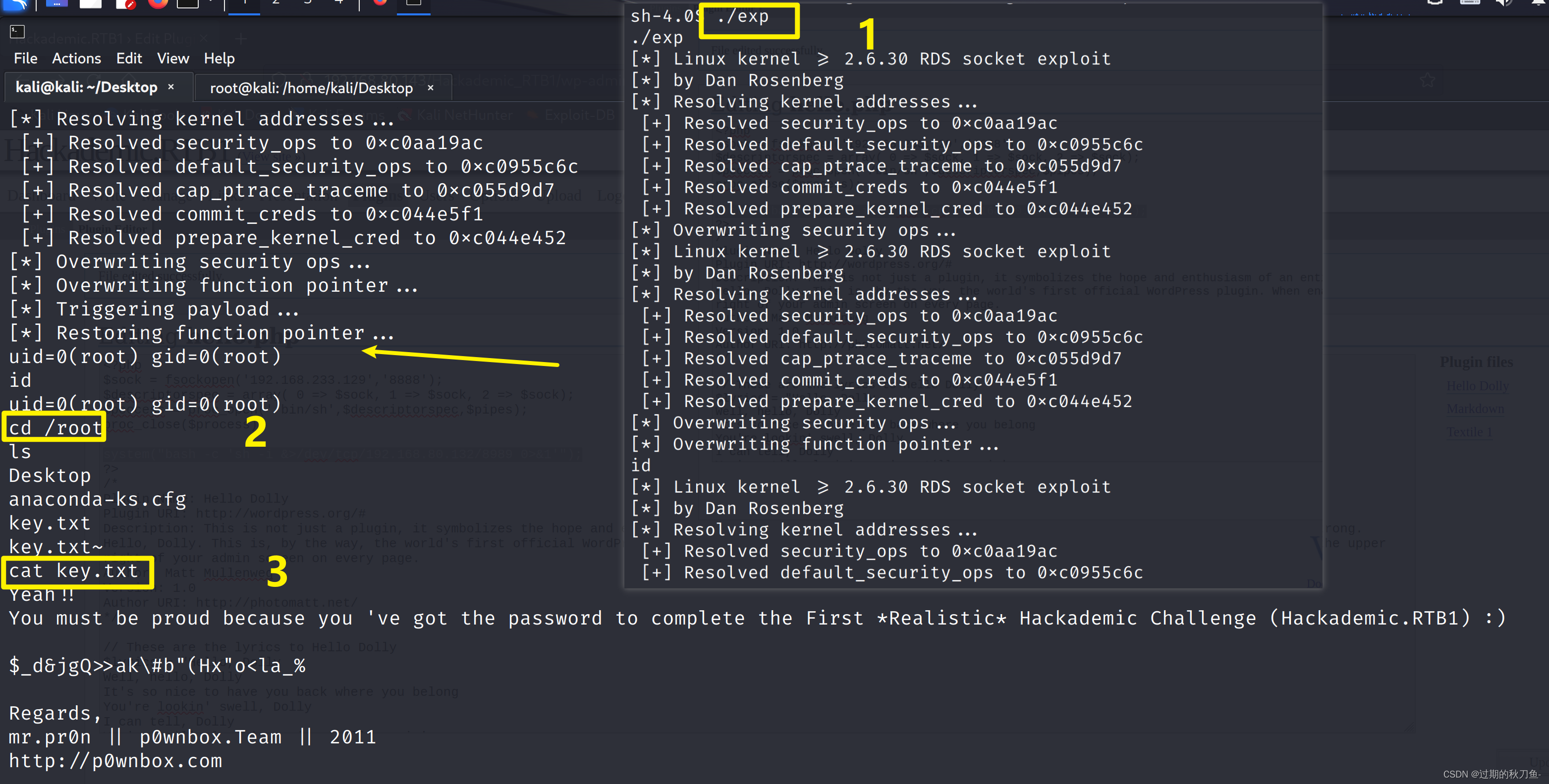
Vulnhub系列靶机--- Hackadmeic.RTB1
系列:Hackademic(此系列共2台) 难度:初级 信息收集 主机发现 netdiscover -r 192.168.80.0/24端口扫描 nmap -A -p- 192.168.80.143访问80端口 使用指纹识别插件查看是WordPress 根据首页显示的内容,点击target 点击…...
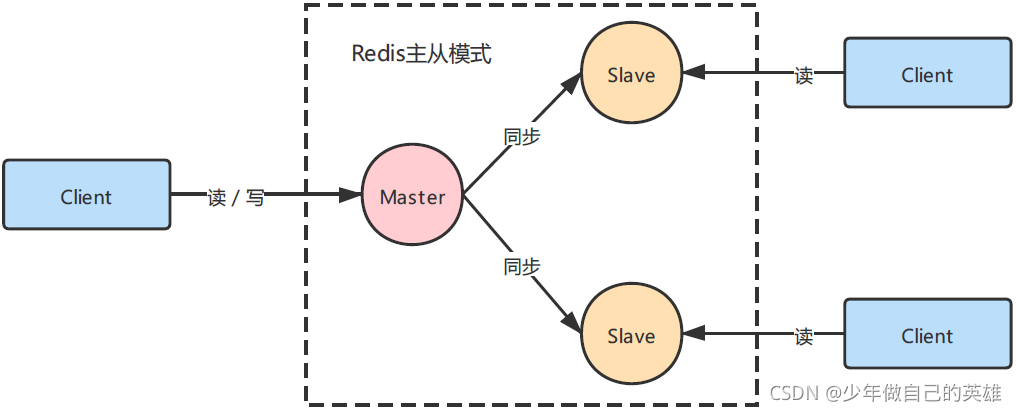
redis高级----------主从复制
redis的四种模式:单例模式;主从模式;哨兵模式,集群模式 一、主从模式 单例模式虽然操作简单,但是不具备高可用 缺点: 单点的宕机引来的服务的灾难、数据丢失单点服务器内存瓶颈,无法无限纵向扩…...

posgresql通过PL/pgSQL脚本统一修改某字段大小写
项目在做postgresql数据库适配时遇到了某些问题,需要统一将某个模式含id字段的全部表,将id字段由小写转换为大写,可以通过PL/pgSQL脚本实现。 先确保当前用户有足够的权限 DO $$ DECLARE current_table text;current_column text; BEGIN --…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...
