当前位置： 首页 > news >正文

一次js请求一般情况下有哪些地方会有缓存处理？

news 2025/10/14 1:38:41

目录

1、DNS缓存

2、CDN缓存

3、浏览器缓存

4、服务器缓存

1、DNS缓存

DNS缓存指DNS返回了正确的IP之后，系统就会将这个结果临时储存起来。并且它会为缓存设定一个失效时间 (例如N小时)，在这N小时之内，当你再次访问这个网站时，系统就会直接从你电脑本地的DNS缓存中把结果交还给你，而不必再去询问DNS服务器，变相“加速”了网址的解析。当然，在超过N小时之后，系统会自动再次去询问DNS服务器获得新的结果。 所以，当你修改了 DNS 服务器，并且不希望电脑继续使用之前的DNS缓存时，就需要手动去清除本地的缓存了。

本地DNS迟迟不生效或者本地dns异常等问题，都会导致访问某些网站出现无法访问的情况，这个时候我们就需要手动清除本地dns缓存，而不是等待！

2、CDN缓存

和Http类似，客户端请求数据时，先从本地缓存查找，如果被请求数据没有过期，拿过来用，如果过期，就向CDN边缘节点发起请求。CDN便会检测被请求的数据是否过期，如果没有过期，就返回数据给客户端，如果过期，CDN再向源站发送请求获取新数据。和买家买货，卖家没货，卖家再进货一个道理^^。

CDN边缘节点缓存机制，一般都遵守http标准协议，通过http响应头中的Cache-Control和max-age的字段来设置CDN边缘节点的数据缓存时间。

3、浏览器缓存

浏览器缓存（Browser Caching）是为了节约网络的资源加速浏览，浏览器在用户磁盘上对最近请求过的文档进行存储，当访问者再次请求这个页面时，浏览器就可以从本地磁盘显示文档，这样就可以加速页面的阅览。

浏览器缓存主要有两类：缓存协商：Last-modified ，Etag 和彻底缓存：cache-control，Expires。浏览器都有对应清除缓存的方法。

4、服务器缓存

服务器缓存有助于优化性能和节省宽带，它将需要频繁访问的Web页面和对象保存在离用户更近的系统中，当再次访问这些对象的时候加快了速度。

相关文章：

一次js请求一般情况下有哪些地方会有缓存处理？

目录 1、DNS缓存 2、CDN缓存 3、浏览器缓存 4、服务器缓存 1、DNS缓存 DNS缓存指DNS返回了正确的IP之后，系统就会将这个结果临时储存起来。并且它会为缓存设定一个失效时间 (例如N小时)，在这N小时之内，当你再次访问这个网站时&#xff0…...

编程日记 2023/8/25 5:27:41

CSDN编程题-每日一练（2023-08-24）

CSDN编程题-每日一练（2023-08-24） 一、题目名称：计算公式二、题目名称：蛇形矩阵三、题目名称：小玉家的电费一、题目名称：计算公式 时间限制：1000ms内存限制：256M 题目描述： 给定整数n。 计算公式： n i-1 ∑ ∑ [gcd(i + j, i - j) = 1] i=1 j=1 输入描述： 输入整数n…...

编程日记 2023/8/25 5:26:37

怎么把PDF转成Word？需要注意什么事项？

PDF是一种常见的文档格式，但是与Word文档不同，PDF文件通常不能直接编辑。如果您想编辑PDF文件中的文本，或者想将PDF文件转换为Word文档，下面我们就来看一看把PDF转成Word有哪些方法和注意事项。 PDF转Word工具 有许多将PDF转换为…...

编程日记 2023/8/25 5:25:36

USACO22OPEN Pair Programming G

P8273 [USACO22OPEN] Pair Programming G 题目大意 一个程序由一系列指令组成，每条指令的类型如下： d \times d d，其中 d d d是一个 [ 0 , 9 ] [0,9] [0,9]范围内的整数 s s s，其中 s s s是一个表示变量名称的字符串&#xff…...

编程日记 2023/8/25 5:24:34

实战分享之springboot+easypoi快速业务集成

1.依赖引入 <!--引入EasyPOI--><dependency><groupId>cn.afterturn</groupId><artifactId>easypoi-base</artifactId><version>4.1.0</version></dependency><dependency><groupId>cn.afterturn</group…...

编程日记 2023/8/25 5:23:33

金字塔原理（思考的逻辑）

前言&#xff1a;前面学习了表达的逻辑&#xff0c;那在表达之前&#xff0c;如何组织内容&#xff1f;如何进行思考&#xff1f;接下来看第二篇——思考的逻辑。 目录 应用逻辑顺序 时间顺序 结构顺序 程度顺序 概括各组思想 什么是概括&#xff1f; 思想表达方式 如…...

编程日记 2023/8/25 5:22:32

机器学习之前向传播（Forward Propagation）和反向传播（Back propagation）

前向传播&#xff08;Forward Propagation&#xff09;和反向传播&#xff08;Back propagation&#xff09;是深度学习中神经网络训练的两个关键步骤。 前向传播&#xff08;Forward Propagation&#xff09;&#xff1a; 定义&#xff1a;前向传播是指从神经网络的输入层到输…...

编程日记 2023/8/25 5:21:31

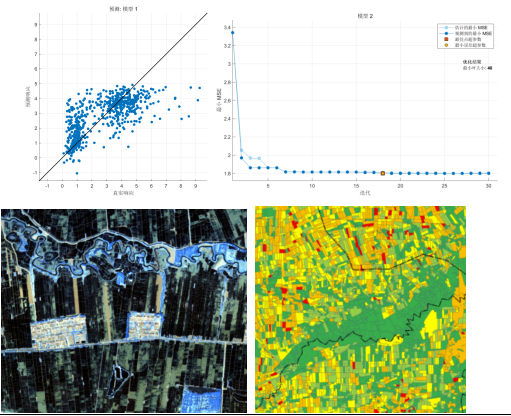
Matlab高光谱遥感数据处理与混合像元分解实践技术

光谱和图像是人们观察世界的两种方式&#xff0c;高光谱遥感通过“图谱合一”的技术创新将两者结合起来&#xff0c;大大提高了人们对客观世界的认知能力&#xff0c;本来在宽波段遥感中不可探测的物质&#xff0c;在高光谱遥感中能被探测。以高光谱遥感为核心&#xff0c;构建…...

编程日记 2023/8/25 5:20:29

Docker consul的容器服务注册与发现

前言一、服务注册与发现二、consul 介绍三、consul 部署3.1 consul服务器3.1.1 建立 Consul 服务3.1.2 查看集群信息3.1.3 通过 http api 获取集群信息 3.2 registrator服务器3.2.1 安装 Gliderlabs/Registrator3.2.2 测试服务发现功能是否正常3.2.3 验证 http 和 nginx 服务是…...

编程日记 2023/8/25 5:19:28

Spring注入外部 工厂类Bean

问题 对于一些使用建造者模式的 Bean&#xff0c;我们往往不能直接 new 出来&#xff0c;这些 Bean 如果需要注册到 Spring 容器中&#xff0c;我们就需要使用工厂类。 比如我们项目中经常使用的okhttp: 如果我们想把OkHttpClient注册到Spring容器中&#xff0c;该怎么做? …...

编程日记 2023/8/25 5:18:26

WPF网格拖动自动布局效果

WPF网格拖动自动布局效果 使用Canvas和鼠标相关事件实现如下的效果： XAML代码： <Window x:Class="CanvasTest.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:...

编程日记 2023/8/25 5:17:25

肯德尔秩相关系数（Kendall‘s Tau）排名

肯德尔秩相关系数&#xff08;Kendall’s Tau&#xff09;是一种用于衡量两个排列之间相似性的统计指标&#xff0c;它考虑了元素之间的顺序关系而不考虑具体数值。该系数被广泛用于排序、排名和比较不同实验结果的相关性等领域。 具体而言&#xff0c;肯德尔秩相关系数衡量了…...

编程日记 2023/8/25 5:16:24

电脑怎么把视频转换gif动图？视频生成gif的操作步骤

如果你也想把一些精彩的视频转gif图片&#xff08;https://www.gif.cn&#xff09;的话&#xff0c;今天的文章你可千万不要错过&#xff0c;利用专业的视频转gif工具&#xff0c;轻松在线视频转gif&#xff0c;操作简单又方便&#xff0c;支持电脑、手机双端操作&#xff0c;赶…...

编程日记 2023/8/25 5:15:23

使用 docker 搭建 granfana+prometheus 监控平台监控测试服务器资源

互联网发展的今天&#xff0c;人们对互联网产品的用户体验要求也越来越高&#xff0c;企业为了能提供更优质的用户体验&#xff0c;就会绞尽脑汁想尽各种办法。而对于服务器的资源监控&#xff0c;搭建一个资源监控平台&#xff0c;就是一个很好的维护优质服务的保障平台。利用…...

编程日记 2023/8/25 5:14:21

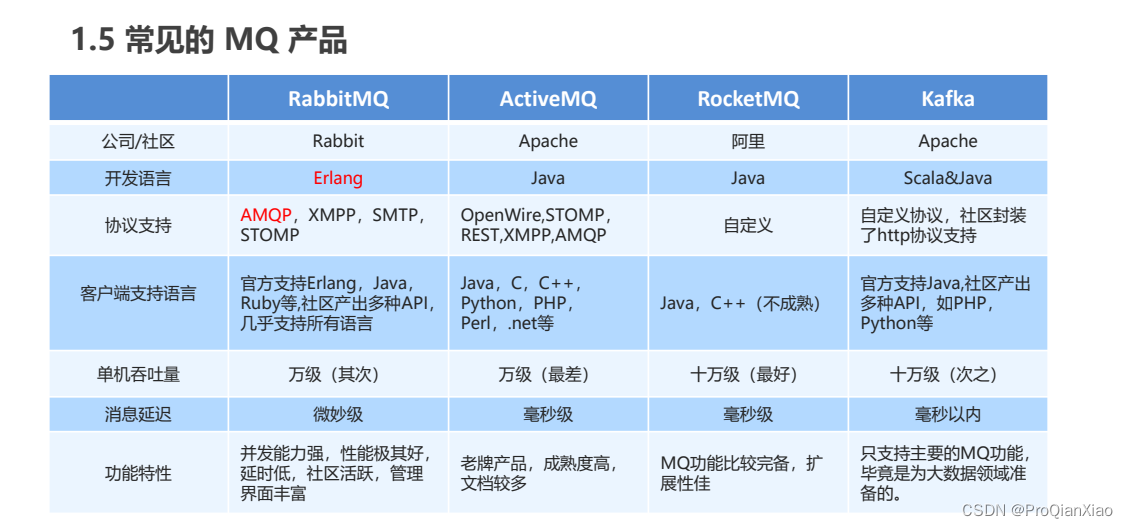
一、MQ的基本概念

1、初识MQ MQ全称是Message Queue&#xff0c;消息队列&#xff0c;多用于系统之间进行异步通信。队列的概念数据结构中有详细介绍过&#xff0c;先进先出&#xff0c;消息队列就是存储消息的数据结构。 同步调用和异步调用两者之间的区别&#xff1a; 同步调用&#xff1a;发…...

编程日记 2023/8/25 5:13:19

Android面试题：MVC、MVP、MVVM

MVC模式&#xff1a; MVC结构&#xff1a; 1.MVC(Model-View-Controller) 2.Model:对数据库的操作、对网络等的操作都应该在Model里面处理&#xff0c;当然对业务计算&#xff0c;变更等操作也是必须放在的该层的。 3.View:主要包括一下View及ViewGroup控件&#xff0c;可以是…...

编程日记 2023/8/25 5:12:18

vue js 回调函数 异步处理 为什么要 let that = this

1 异步就是开个事务(只有主线程 等主线程空闲),用that 值 做处理,然后返回处理结果,而that的值是开启事务那一刻的this的值.而在主线程处理的时候,this的一直在变化, that的值保留在那一刻 ps 或是将本obj 传递给其他的obj使用处理 ps 开启新事务或开启新子线程都是 在新的ob…...

编程日记 2023/8/25 5:11:16

前端面试：【算法与数据结构】常见数据结构解析

在计算机科学中&#xff0c;数据结构是组织和存储数据的方式。精通常见的数据结构对于解决计算机科学和编程问题至关重要。本文将深入探讨常见的数据结构&#xff1a;数组、链表、栈、队列和哈希表&#xff0c;以帮助你建立坚实的数据结构基础。 1. 数组&#xff08;Array&…...

编程日记 2023/8/25 5:10:15

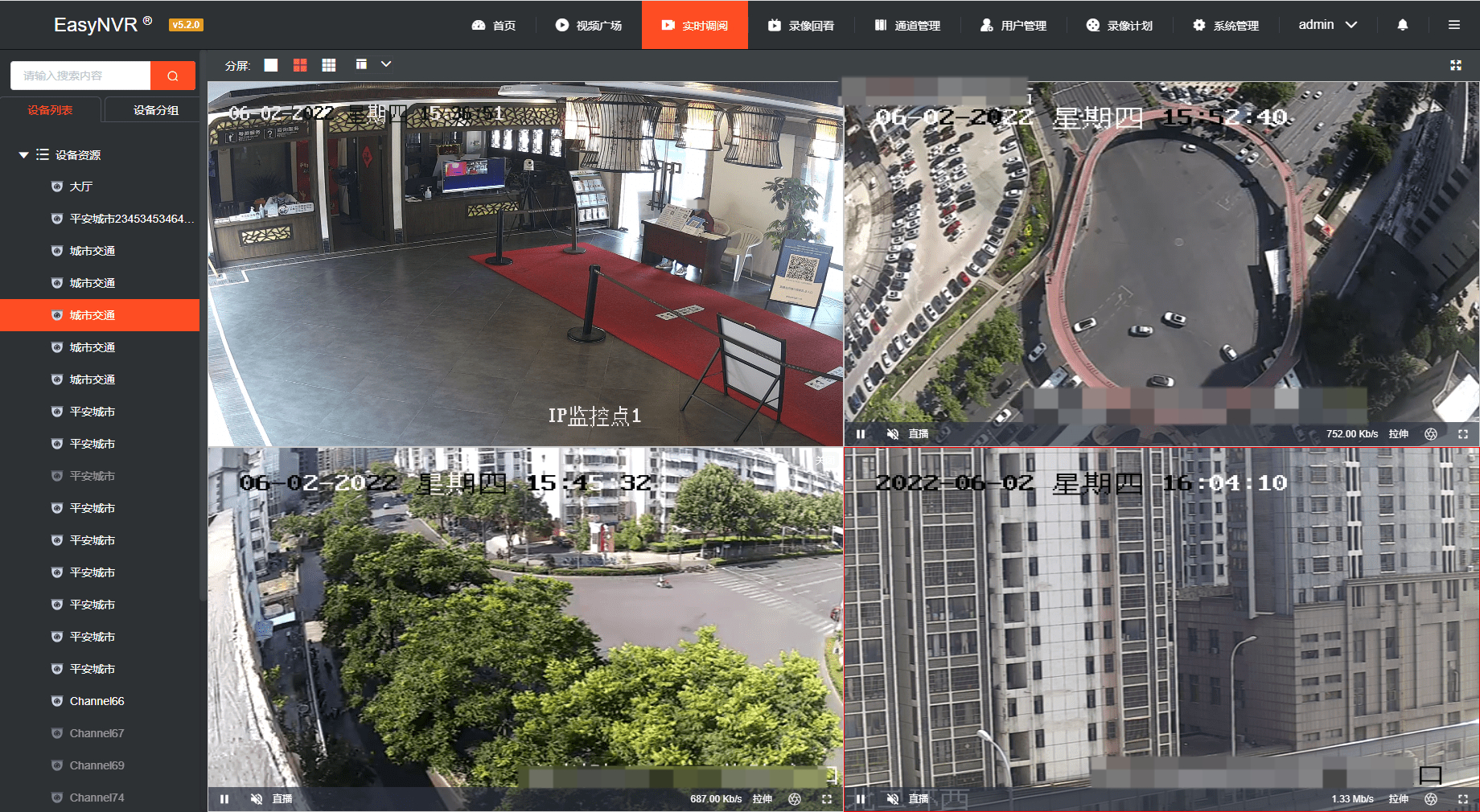
RTSP/Onvif视频服务器EasyNVR安防视频云服务平台出现崩溃并重启的情况解决方案

EasyNVR安防视频云服务平台的特点是基于RTSP/Onvif协议将前端设备统一接入&#xff0c;在平台进行转码、直播、处理及分发&#xff0c;在安防监控场景中&#xff0c;EasyNVR可实现实时监控、云端录像、云存储、告警、级联等视频能力&#xff0c;极大满足行业的视频监控需求。 有…...

编程日记 2023/8/25 5:09:14

软考高级系统架构设计师系列论文九十四：论计算机网络的安全性设计

软考高级系统架构设计师系列论文九十四：论计算机网络的安全性设计 一、计算机网络安全性设计相关知识点二、摘要三、正文四、总结一、计算机网络安全性设计相关知识点 软考高级系统架构设计师：计算机网络...

编程日记 2023/8/25 5:08:13

iOS 26 携众系统重磅更新，但“苹果智能”仍与国行无缘

美国西海岸的夏天&#xff0c;再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至&#xff0c;这不仅是开发者的盛宴&#xff0c;更是全球数亿苹果用户翘首以盼的科技春晚。今年&#xff0c;苹果依旧为我们带来了全家桶式的系统更新&#xff0c;包括 iOS 26、iPadOS 26…...

编程新知 2025/10/12 1:24:52

边缘计算医疗风险自查APP开发方案

核心目标：在便携设备（智能手表/家用检测仪）部署轻量化疾病预测模型，实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

编程新知 2025/10/8 22:42:04

2.Vue编写一个app

1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

编程新知 2025/10/10 15:46:36

【单片机期末】单片机系统设计

主要内容&#xff1a;系统状态机&#xff0c;系统时基&#xff0c;系统需求分析&#xff0c;系统构建&#xff0c;系统状态流图 一、题目要求 二、绘制系统状态流图 题目&#xff1a;根据上述描述绘制系统状态流图&#xff0c;注明状态转移条件及方向。 三、利用定时器产生时…...

编程新知 2025/10/5 1:54:55

QT： `long long` 类型转换为 `QString` 2025.6.5

在 Qt 中&#xff0c;将 long long 类型转换为 QString 可以通过以下两种常用方法实现&#xff1a; 方法 1&#xff1a;使用 QString::number() 直接调用 QString 的静态方法 number()&#xff0c;将数值转换为字符串&#xff1a; long long value 1234567890123456789LL; …...

编程新知 2025/9/30 0:01:36

华为云Flexus+DeepSeek征文｜DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建

华为云FlexusDeepSeek征文&#xff5c;DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色&#xff0c;华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型&#xff0c;能助力我们轻松驾驭 DeepSeek-V3/R1&#xff0c;本文中将分享如何…...

编程新知 2025/9/30 3:12:52

【论文阅读28】-CNN-BiLSTM-Attention-（2024）

本文把滑坡位移序列拆开、筛优质因子&#xff0c;再用 CNN-BiLSTM-Attention 来动态预测每个子序列&#xff0c;最后重构出总位移&#xff0c;预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵&#xff08;S…...

编程新知 2025/10/2 3:36:21

初学 pytest 记录

安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

编程新知 2025/9/22 16:24:18

华硕a豆14 Air香氛版，美学与科技的馨香融合

在快节奏的现代生活中&#xff0c;我们渴望一个能激发创想、愉悦感官的工作与生活伙伴&#xff0c;它不仅是冰冷的科技工具&#xff0c;更能触动我们内心深处的细腻情感。正是在这样的期许下&#xff0c;华硕a豆14 Air香氛版翩然而至&#xff0c;它以一种前所未有的方式&#x…...

编程新知 2025/9/28 3:34:22

九天毕昇深度学习平台 | 如何安装库？

pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子&#xff1a; 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

编程新知 2025/9/28 7:36:19