深度学习神经网络基础知识(二)权重衰减、暂退法(Dropout)
专栏:神经网络复现目录
深度学习神经网络基础知识(二)
本文讲述神经网络基础知识,具体细节讲述前向传播,反向传播和计算图,同时讲解神经网络优化方法:权重衰减,Dropout等方法,最后进行Kaggle实战,具体用一个预测房价的例子使用上述方法。
文章部分文字和代码来自《动手学深度学习》
文章目录
- 深度学习神经网络基础知识(二)
- 范数
- 权重衰减
- 定义
- 权重衰减的从零实现
- 运行结果
- 权重衰减的简洁实现
- 暂退法(Dropout)
- 定义
- 暂退法的从零实现
- 运行结果
- 暂退法的简洁实现
范数
LpL_pLp范数是一种向量范数,定义如下:
∣x∣p=(∣x1∣p+∣x2∣p+⋯+∣xn∣p)1p\left|\boldsymbol{x}\right|{p}=\left(\left|x{1}\right|^{p}+\left|x_{2}\right|^{p}+\cdots+\left|x_{n}\right|^{p}\right)^{\frac{1}{p}}∣x∣p=(∣x1∣p+∣x2∣p+⋯+∣xn∣p)p1
其中,p≥1p \geq 1p≥1,x=(x1,x2,⋯,xn)\boldsymbol{x}=(x_1, x_2, \cdots, x_n)x=(x1,x2,⋯,xn) 是一个 nnn 维向量。当 p=2p=2p=2 时,LpL_pLp范数也称为欧几里得范数(Euclidean norm),常用于表达向量的长度或者大小。当 p=1p=1p=1 时,LpL_pLp范数也称为曼哈顿范数(Manhattan norm)或者 ℓ1\ell_1ℓ1范数,常用于表达向量中各个元素的绝对值之和。当 p→∞p \rightarrow \inftyp→∞ 时,LpL_pLp范数也称为切比雪夫范数(Chebyshev norm)或者 ℓ∞\ell_\inftyℓ∞ 范数,常用于表达向量中绝对值最大的元素。
L0L_0L0范数不是向量范数,因为它并不满足向量范数的三个条件之一,即正定性。通常把向量 x\boldsymbol{x}x 中非零元素的个数称为 x\boldsymbol{x}x 的 L0L_0L0 范数,但这并不是一个数学上合理的定义。
常见的范数有以下几种:
L1L^1L1 范数:∣∣x∣∣1=∑i=1n∣xi∣||x||1 = \sum{i=1}^n |x_i|∣∣x∣∣1=∑i=1n∣xi∣
L2L^2L2 范数:∣∣x∣∣2=∑i=1nxi2||x||2 = \sqrt{\sum{i=1}^n x_i^2}∣∣x∣∣2=∑i=1nxi2
权重衰减
定义
权重衰减是一种用于降低过拟合的正则化技术。其原理是通过在模型训练过程中增加一个惩罚项(也称作正则化项),来抑制模型的复杂度,从而达到减小过拟合的效果。
具体来说,在损失函数中添加一个正则化项,一般会对模型的参数进行L2L_2L2范数的约束,也就是让模型的参数尽量小。这样,在模型训练过程中,不仅会尽量减小训练数据的损失,还会尽量让模型参数的平方和小,从而达到抑制模型过拟合的效果。
权重衰减的损失函数为:

其中 L(w,b)\mathcal{L}(\boldsymbol{w}, b)L(w,b) 是原始的无正则化项的损失函数,∣w∣2|\boldsymbol{w}|^2∣w∣2 表示模型参数的L2L_2L2范数,λ\lambdaλ 是正则化强度,nnn 是训练样本数。
在优化算法中,我们需要对这个损失函数进行梯度下降。由于正则化项的梯度为 λnw\frac{\lambda}{n}\boldsymbol{w}nλw,因此我们需要对原始的梯度加上这个正则化项的梯度:
w←(1−ηλ∣B∣)w−η∣B∣∑i∈B∂∂wl(i)(w,b)w \leftarrow (1 - \frac{\eta \lambda}{|B|})w - \frac{\eta}{|B|} \sum_{i \in B} \frac{\partial}{\partial w} l^{(i)}(w, b) w←(1−∣B∣ηλ)w−∣B∣ηi∈B∑∂w∂l(i)(w,b)
其中,www是待更新的权重参数,η\etaη是学习率,λ\lambdaλ是正则化超参数(即权重衰减超参数),∣B∣|B|∣B∣是当前小批量中的样本数,l(i)(w,b)l^{(i)}(w, b)l(i)(w,b)是第iii个样本的损失函数,∂∂wl(i)(w,b)\frac{\partial}{\partial w} l^{(i)}(w, b)∂w∂l(i)(w,b)是对权重参数的损失函数梯度。
权重衰减的从零实现
构造生成数据集的函数
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
#生成数据集
def synthetic_data(w,b,num):#x通过正态分布生成x=torch.normal(0,1,(num,len(w)))y=torch.matmul(x,w)+b#数据集中加入噪声y+=torch.normal(0,0.01,y.shape)return x,y.reshape(-1,1)
构造一个数据迭代器
def load_array(data_arrays, batch_size, is_train=True): #@save"""构造一个PyTorch数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)
生成数据集
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = synthetic_data(true_w, true_b, n_train)
train_iter = load_array(train_data, batch_size)
test_data = synthetic_data(true_w, true_b, n_test)
test_iter = load_array(test_data, batch_size, is_train=False)
初始化模型参数
def init_params():w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)b = torch.zeros(1, requires_grad=True)return [w, b]
定义L2范数惩罚
def l2_penalty(w):return torch.sum(w.pow(2)) / 2
训练
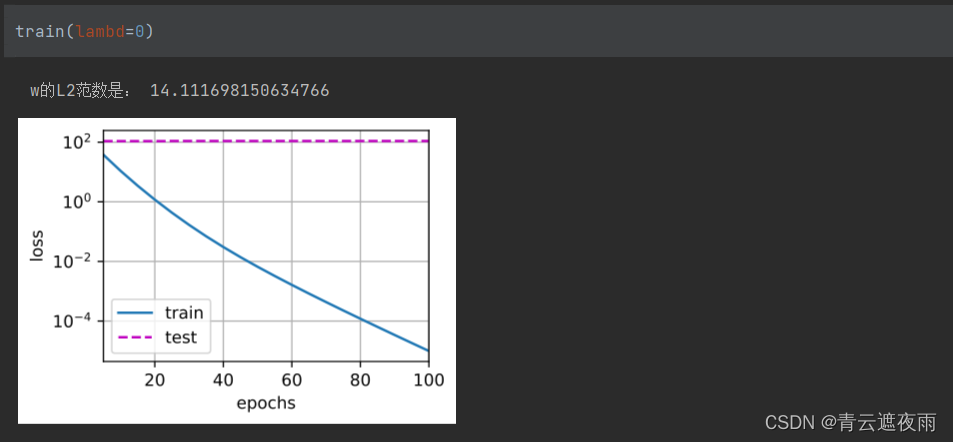
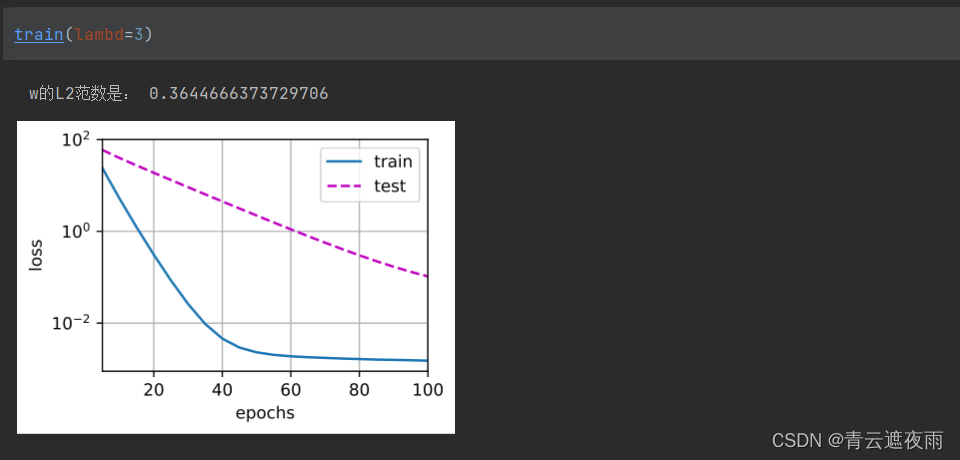
def train(lambd):w, b = init_params()net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_lossnum_epochs, lr = 100, 0.003animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])for epoch in range(num_epochs):for X, y in train_iter:# 增加了L2范数惩罚项,# 广播机制使l2_penalty(w)成为一个长度为batch_size的向量l = loss(net(X), y) + lambd * l2_penalty(w)l.sum().backward()d2l.sgd([w, b], lr, batch_size)if (epoch + 1) % 5 == 0:animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数是:', torch.norm(w).item())
运行结果
未使用权重衰减
使用权重衰减
权重衰减的简洁实现
def train_concise(weight_decay):net = nn.Sequential(nn.Linear(num_inputs, 1))for param in net.parameters():param.data.normal_()loss = nn.MSELoss(reduction='none')num_epochs, lr = 100, 0.003# 偏置参数没有衰减trainer = optim.SGD(model.parameters(), lr=lr, weight_decay=weight_decay)animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])for epoch in range(num_epochs):for X, y in train_iter:trainer.zero_grad()l = loss(net(X), y)l.mean().backward()trainer.step()if (epoch + 1) % 5 == 0:animator.add(epoch + 1,(d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数:', net[0].weight.norm().item())
关注这行代码
trainer = optim.SGD(model.parameters(), lr=lr, weight_decay=weight_decay)
其中weight_decay参数即为lambda
暂退法(Dropout)
定义
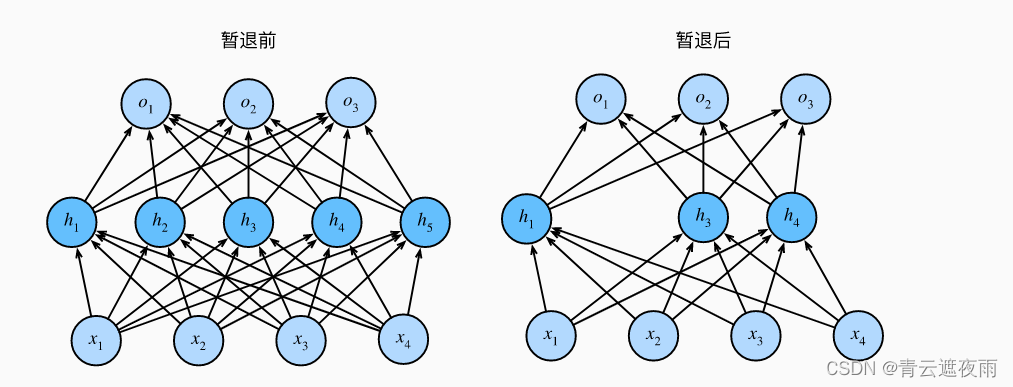
Dropout是一种用于神经网络的正则化技术,旨在减少模型的过拟合。该算法的核心思想是在网络的训练过程中随机“丢弃”一部分神经元,从而强制模型学习更加鲁棒和通用的特征。在测试时,所有神经元都保留,但是输出值需要乘以一个固定比例以保持期望输出不变。
具体来说,假设我们有一个包含LLL个层的神经网络。对于第iii层,它的输出为h(i)h^{(i)}h(i)。在训练时,我们按照一定的概率ppp来随机选择一部分神经元,将它们的输出值设置为0。因此,第iii层的输出为:
h~(i)=r(i)⊙h(i)\tilde{h}^{(i)}=r^{(i)}\odot h^{(i)}h~(i)=r(i)⊙h(i)
其中r(i)r^{(i)}r(i)是一个与h(i)h^{(i)}h(i)具有相同形状的二进制向量,其中元素值为1的概率为ppp,值为0的概率为1−p1-p1−p,⊙\odot⊙表示按元素相乘。在前向传播过程中,我们使用h~(i)\tilde{h}^{(i)}h~(i)代替h(i)h^{(i)}h(i)进行计算。在反向传播过程中,由于某些神经元的输出被设置为0,我们只需要将其对应的梯度清零即可。
在测试时,我们需要保留所有神经元的输出,但是为了保持期望输出不变,我们需要将所有神经元的输出值乘以ppp,即:
htest(i)=p⋅h(i)h^{(i)}_{test}=p\cdot h^{(i)}htest(i)=p⋅h(i)
下图形象的展示了暂退法的效果:
暂退法的从零实现
这是一个实现dropout算法的函数,它接受一个输入张量X和一个dropout概率dropout,然后返回一个应用了dropout的输出张量。
具体来说,该函数会生成一个与X形状相同的掩码张量,其中每个元素都是随机生成的0或1,生成方式是根据概率dropout与0比较,如果大于dropout则为1,否则为0。然后将掩码张量与X相乘并除以(1 - dropout),这个操作相当于将保留下来的元素值除以它们的概率。最后返回应用了dropout的输出张量。
import torch
from torch import nn
from d2l import torch as d2ldef dropout_layer(X, dropout):assert 0 <= dropout <= 1# 在本情况中,所有元素都被丢弃if dropout == 1:return torch.zeros_like(X)# 在本情况中,所有元素都被保留if dropout == 0:return Xmask = (torch.rand(X.shape) > dropout).float()return mask * X / (1.0 - dropout)
具体关注一下:
mask = (torch.rand(X.shape) > dropout).float()
这一行代码的作用是生成一个与X形状相同的张量mask,并且其中的每个元素都是0或1。这里的0和1表示相应的X元素是否被保留,而生成这些0和1的方式是随机的,因为我们用torch.rand()函数生成一个形状与X相同的随机张量,并将其中的每个元素与dropout做比较。
比较的结果是一个布尔类型的张量,即对于X中的每个元素,如果随机生成的相应元素的值大于dropout,那么在mask中相应位置的值为1,表示保留;反之,如果随机生成的值小于等于dropout,那么在mask中相应位置的值为0,表示丢弃。
最后,为了保持期望的值不变,我们将所有保留的元素的值除以 1- dropout,这是因为被保留的概率是1- dropout。所以,最终得到的输出是一个X的掩码版本,其中的一些元素被随机置为零。
测试一下我们写的dropout层
X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))
定义模型参数
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
定义模型
这次我们使用了和以往不同、面向对象的模型定义方式,需要重写__init__和forward函数
init 方法用于定义网络结构,包括网络层、激活函数、损失函数等,并初始化权重、偏差等参数。这些网络参数在训练过程中会不断地更新。
forward 方法用于定义数据在网络中的正向传播(也就是模型从输入到输出的计算过程),即输入数据经过网络的各层计算,最终得到输出。在该方法中,我们可以任意组合各种网络层及其参数,实现自己所需要的网络结构和计算过程。
在下面的代码中,Net 类继承自 nn.Module,其中 init 方法用于定义网络的结构,包括三个全连接层和一个 ReLU 激活函数。forward 方法用于实现数据在网络中的正向传播计算,包括将输入 X 经过全连接层和激活函数得到输出 out。在训练模式中,还会在第一个全连接层和第二个全连接层后面添加 dropout 层。
dropout1, dropout2 = 0.2, 0.5class Net(nn.Module):def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,is_training = True):super(Net, self).__init__()self.num_inputs = num_inputsself.training = is_trainingself.lin1 = nn.Linear(num_inputs, num_hiddens1)self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)self.lin3 = nn.Linear(num_hiddens2, num_outputs)self.relu = nn.ReLU()def forward(self, X):H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))# 只有在训练模型时才使用dropoutif self.training == True:# 在第一个全连接层之后添加一个dropout层H1 = dropout_layer(H1, dropout1)H2 = self.relu(self.lin2(H1))if self.training == True:# 在第二个全连接层之后添加一个dropout层H2 = dropout_layer(H2, dropout2)out = self.lin3(H2)return outnet = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)
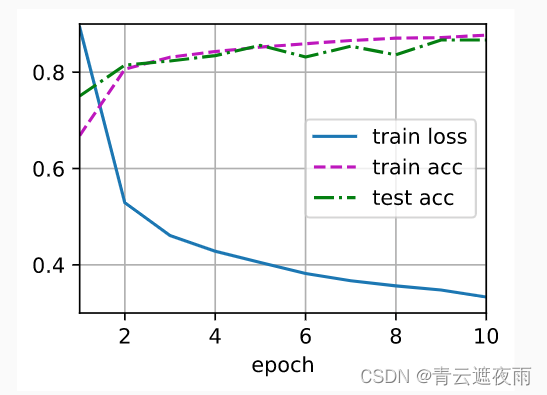
训练和测试
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
运行结果
暂退法的简洁实现
net = nn.Sequential(nn.Flatten(),nn.Linear(784, 256),nn.ReLU(),# 在第一个全连接层之后添加一个dropout层nn.Dropout(dropout1),nn.Linear(256, 256),nn.ReLU(),# 在第二个全连接层之后添加一个dropout层nn.Dropout(dropout2),nn.Linear(256, 10))def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, std=0.01)net.apply(init_weights);
或者是
class Net(nn.Module):def __init__(self, input_size, hidden_size, output_size, dropout_prob):super(Net, self).__init__()self.fc1 = nn.Linear(input_size, hidden_size)self.fc2 = nn.Linear(hidden_size, hidden_size)self.fc3 = nn.Linear(hidden_size, output_size)self.dropout = nn.Dropout(p=dropout_prob)def forward(self, x):x = torch.relu(self.fc1(x))x = self.dropout(x)x = torch.relu(self.fc2(x))x = self.dropout(x)x = self.fc3(x)return x
相关文章:

深度学习神经网络基础知识(二)权重衰减、暂退法(Dropout)
专栏:神经网络复现目录 深度学习神经网络基础知识(二) 本文讲述神经网络基础知识,具体细节讲述前向传播,反向传播和计算图,同时讲解神经网络优化方法:权重衰减,Dropout等方法,最后进行Kaggle实…...

[面试直通版]网络协议面试核心之HTTP,HTTPS,DNS-DNS安全
点击->计算机网络复习的文章集<-点击 目录 典型问题: 部分现象 DNS劫持 DNS欺骗 DDoS攻击 典型问题: 什么是DNS劫持,DNS欺骗,是什么原理如何防范DNS攻击? 部分现象 错误域名解析到纠错导航页面错误域名解析…...

【OJ】A+B=X
📚Description: 数列S中有n个整数,判断S中是否存在两个数A、B,使之和等于X。 ⏳Input: 第一行为T,输入包括T组测试数据。 每组数据第一行包括两个数字n和X,第二行有n个整数,表示数列S,(1&l…...

Python实现性能自动化测试,还可以如此简单
Python实现性能自动化测试,还可以如此简单 目录:导读 一、思考❓❔ 二、基础操作🔨🔨 三、综合案例演练🔨🔨 四、总结💡💡 写在最后 一、思考❓❔ 1.什么是性能自动化测试? 性…...

Leetcode力扣秋招刷题路-0080
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结 80. 删除有序数组中的重复项 II 给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长…...
Java实现JDBC工具类DbUtils的抽取及程序实现数据库的增删改操作
封装DbUtils 工具类 不知道我们发现没有,不管是对数据库进行查询,还是标准的JDBC 步骤,其开端都是先实现JDBC 的加载注册,接着是获取数据库的连接,最后都是实现关闭连接,释放资源的操作。那我们何不直接把…...

【docker】拉取镜像环境报错解决#ERROR: Get https://registry-1.docker.io/v2/
🍁博主简介 🏅云计算领域优质创作者 🏅华为云开发者社区专家博主 🏅阿里云开发者社区专家博主 💊交流社区:运维交流社区 欢迎大家的加入! 文章目录问题报错原因解决方法问题 ERROR…...
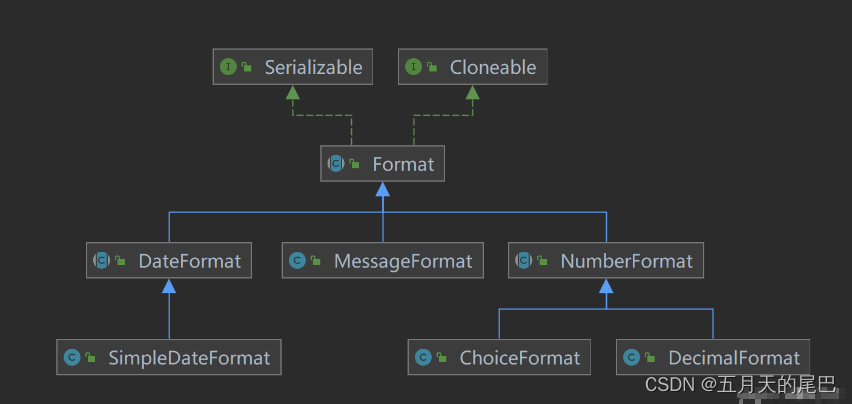
java中NumberFormat 、DecimalFormat的介绍及使用,java数字格式化,BigDecimal数字格式化
文章目录前言一、NumberFormat1、概述2、实例化方法3、货币格式化4、百分比格式化5、NumberFormat的坑5.1、不同的格式化对象处理相同数值返回结果不同问题源码分析:二、DecimalFormat1、概述2、常用方法3、字符及含义0与#的区别分组分隔符的使用“%” 将数字乘以10…...

2023什么是分销商城系统?营销,核心功能
大家好,我是你们熟悉而又陌生的好朋友梦龙,一个创业期的年轻人 分销商城是指由网络营销运营商提供的,用于协助供给商搭建、管理及运作其网络销售渠道,协助分销商获取货源渠道的平台。简单来说,就是企业应用无线裂变分…...

天翼数字生活C++客户端实习
面试C客户端实习的岗位,相对不难 面试官:实习主要做的是国产操作系统下的应用,主要做的是视频监控、安防相关的工具,具体就是一个叫做 天翼云眼的软件,目前在windows下和电视下都有对应的应用,就是现在想在…...

Java 接口
文章目录1、接口的概念2、接口的定义3、接口的使用4、接口和抽象类1、接口的概念 类是一种具体的实现体,而接口定义了一种规范(抽象方法),接口定义了某一批类所需要遵循的规范,接口不关心类内部的属性和方法的具体实现…...

【React】react-router 路由详解
🚩🚩🚩 💎个人主页: 阿选不出来 💨💨💨 💎个人简介: 一名大二在校生,学习方向前端,不定时更新自己学习道路上的一些笔记. 💨💨💨 💎目…...

DaVinci 偏好设置:系统 - 内存和 GPU
偏好设置 - 系统/内存和 GPUPreferences - System/Memory and GPU内存和 GPU Memory and GPU 选项卡提供了内存配置以及 GPU 配置的相关设置。内存配置Memory Configuration系统内存System Memory列出了所用电脑的总的可用内存。限制 Resolve 内存使用到Limit Resolve memory u…...
- 教你认清楚YUV420P和YUV420SP的真正差异在哪里)
视频知识点(22)- 教你认清楚YUV420P和YUV420SP的真正差异在哪里
*《音视频开发》系列-总览* 前言 在视频技术领域,存在着非常多的颜色空间模型,YUV颜色空间就是其中之一。我们没有必要把所有的颜色空间都搞明白,只需要关注自己所从事的领域的常用颜色空间模型即可,同样,YUV颜色空间模型也有非常多的子类型,我们也没有必要都搞得清清楚楚…...

企业电子招标采购系统源码Spring Cloud + Spring Boot + MybatisPlus + Redis + Layui
项目说明 随着公司的快速发展,企业人员和经营规模不断壮大,公司对内部招采管理的提升提出了更高的要求。在企业里建立一个公平、公开、公正的采购环境,最大限度控制采购成本至关重要。符合国家电子招投标法律法规及相关规范,以及…...

面试常问-Alpha测试和Beta测试
Alpha测试 Alpha测试是一种验收测试,在识别典型用户可能执行的任务并对其进行测试之前,执行该测试是为了识别所有可能的问题和错误。 尽可能简单地说,这种测试之所以被称为alpha,只是因为它是在软件开发的早期、接近开发结束时和…...

html理论基础
组织:中国互动出版网(http://www.china-pub.com/)RFC文档中文翻译计划(http://www.china-pub.com/compters/emook/aboutemook.htm)E-mail:ouyangchina-pub.com译者:黄俊(hujiao hj_c…...

【安卓开发】数据存储全方案--详解持久化技术
读书笔记系列:第一行代码 Android 6.1 持久化技术简介 三种数据持久化方式:文件存储、SharedPreference存储以及数据库存储,除此之外还可以存储在SD卡中(不安全) 6.2 文件存储 该方法不对存储的内容做格式化处理都…...

Vue项目实战
一、产品开发的大致流程 一般公司流程如下: 1、产品经理设计产品原型图 2、UI设计师设计符合需求的原型UI图 3、前端100%还原高保真UI设计图 4、后端设计接口 5、前后端接口联调 6、前后端功能自测 7、测试、运维进行产品的测试和上线 一般大型公司流程如下&…...

Github 学生优惠包 -- 最新防踩坑指南
Github学生优惠包的申请最近越来越麻烦,里面有非常多的坑,留下此文防止各位申请的时候踩到。 此文面向中国大陆真正有学生身份的同学!!! 文章目录前言1.用到的网址2.申请所需3.详细步骤4.踩坑点前言 记得在一年以前还…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
