手撕 `np.transpose` : 三维数组的循环转置
手撕 np.transpose : 三维数组的循环转置
手撕 np.transpose 2D
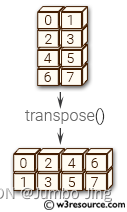
- 何为transpose ?
如上图: 二维的例子, 直观地理解就是沿着对角线拉平(对角关系左上右下依旧), 其他位置依次填充.
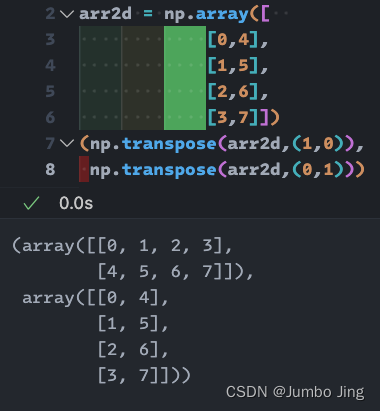
2. 2D数组中0,1 为原始参, 1,0 为转置参
- 原始参即数组的原始形态: 比如👆🏻shape为(4,2), 调用元参 即复原原始状态, 即使数组转置本身(自转)也是一样.
- 转置参为转置形态: 👆🏻shape为(2,4), 调用转参 即进入转置状态, 当数组转置本身时, 数组会在(2,4)和(4,2)互相转换. 在2D矩阵中和.T相同 👇
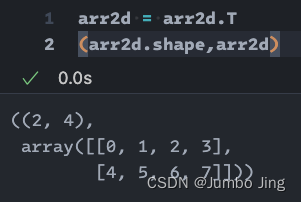
3. np.flip 和 np.rot90
- rot90 : 逆时针躺平(
k=1) - flip 翻转: 👇🏻shape不变, 翻转180°, 相当于连续
rot902次
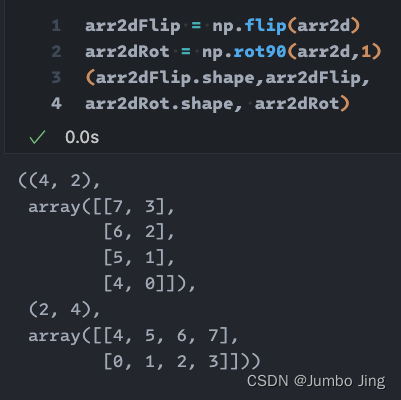
手撕3D转置:
- 源阵:
arr = np.array([[[11,12,13,14], [21,22,23,24], [31,32,33,34]],[[41,42,43,44], [51,52,53,54], [61,62,63,64]]])
(arr.shape, arr)大-中-小(zyx)
((2, 3, 4),array([[[11, 12, 13, 14],[21, 22, 23, 24],[31, 32, 33, 34]],[[41, 42, 43, 44],[51, 52, 53, 54],[61, 62, 63, 64]]]))参数2, 轴 (0,1,2)
撕! 撕! 撕!
公转
012–zyx- shape: 大-中-小
arr012 = np.transpose(arr,(0,1,2))
(arr012.shape, arr012)((2, 3, 4),array([[[11, 12, 13, 14],[21, 22, 23, 24],[31, 32, 33, 34]],[[41, 42, 43, 44],[51, 52, 53, 54],[61, 62, 63, 64]]]))
021–zxy- shape: 大-小-中
...
((2, 4, 3),array([[[11, 21, 31],[12, 22, 32],[13, 23, 33],[14, 24, 34]],[[41, 51, 61],[42, 52, 62],[43, 53, 63],[44, 54, 64]]]))
120–yzx- shape: 中-大-小
...
((3, 4, 2),array([[[11, 41],[12, 42],[13, 43],[14, 44]],[[21, 51],[22, 52],[23, 53],[24, 54]],[[31, 61],[32, 62],[33, 63],[34, 64]]]))
102–yxz- shape: 中-小-大
...
((3, 2, 4),array([[[11, 12, 13, 14],[41, 42, 43, 44]],[[21, 22, 23, 24],[51, 52, 53, 54]],[[31, 32, 33, 34],[61, 62, 63, 64]]]))
201–xzy- shape: 小-大-中
((4, 2, 3),array([[[11, 21, 31],[41, 51, 61]],[[12, 22, 32],[42, 52, 62]],[[13, 23, 33],[43, 53, 63]],[[14, 24, 34],[44, 54, 64]]]))
210–xyz- shape: 小-中-大
((4, 3, 2),array([[[11, 41],[21, 51],[31, 61]],[[12, 42],[22, 52],[32, 62]],[[13, 43],[23, 53],[33, 63]],[[14, 44],[24, 54],[34, 64]]]))
自转
- 数组转置自身时变化:
arr012 = np.transpose(arr012,(0,1,2))
(arr012.shape, arr012)
...
元 参: 012 <-------一阶转参: 021 <–> 012一阶转参: 102 <–> 012一阶转参: 210 <–> 012二阶转参: 120 --> 201 --> 012 --> 120 …二阶转参: 201 --> 120 --> 012 --> 201 …
结论:
-
3D转置 在本例中,
元参为012用于还原原始结构, 一阶转参有3个, 在数组转置自身, 会和元参互相转换,相当于.T(瞎猜的) -
重点来了, 3D矩阵有2个二阶
转参很有意思, 在数组转置自身时, 这2个参数会和元参一起构成闭环形成三种转置状态无限循环.- 注意⚠️: 顺序是先找到另一个
转参, 在通过元参, 找回自身.
- 注意⚠️: 顺序是先找到另一个
-
3D转置 本身很抽象, 通过本次手撕实验观察到以下结果:
- 对角铁律: 在大阵中, 第一个元素和最后一个元素永远是第一个元素和最后一个元素
- 相邻铁律: 在中阵中,第一个元素和最后一个元素相邻关系不变
- 相差铁律: 在小阵中, 元素之间的index差值在同一维度永远为1
- 💡: 本文好几个名词是我自己杜xia撰bian的, 本文是被3D转置搞得头疼又停不下来逼出来的别太当真…
具体意义, 留待下文分解
<<未完待续>>
相关文章:

手撕 `np.transpose` : 三维数组的循环转置
手撕 np.transpose : 三维数组的循环转置 手撕 np.transpose 2D 何为transpose ? 如上图: 二维的例子, 直观地理解就是沿着对角线拉平(对角关系左上右下依旧), 其他位置依次填充. 2. 2D数组中0,1 为原始参, 1,0 为转置参 - 原始参即数组的原始形态: 比如👆&#x…...
计算机竞赛 基于Django与深度学习的股票预测系统
文章目录 0 前言1 课题背景2 实现效果3 Django框架4 数据整理5 模型准备和训练6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 **基于Django与深度学习的股票预测系统 ** 该项目较为新颖,适合作为竞赛课题方向ÿ…...

CSS 小技能(一):HTML 两个图片竖着平铺、设置图片点击、设置滚动条颜色
下面的代码没有考虑响应式的效果,如果考虑的话还需要一些代码进行处理。 【注】当时写的时候仅考虑了 webkit 内核的浏览器,如果是 IE 或者其他浏览器,请增加额外的 CSS 样式进行控制。 <!DOCTYPE html> <html> <head>&l…...
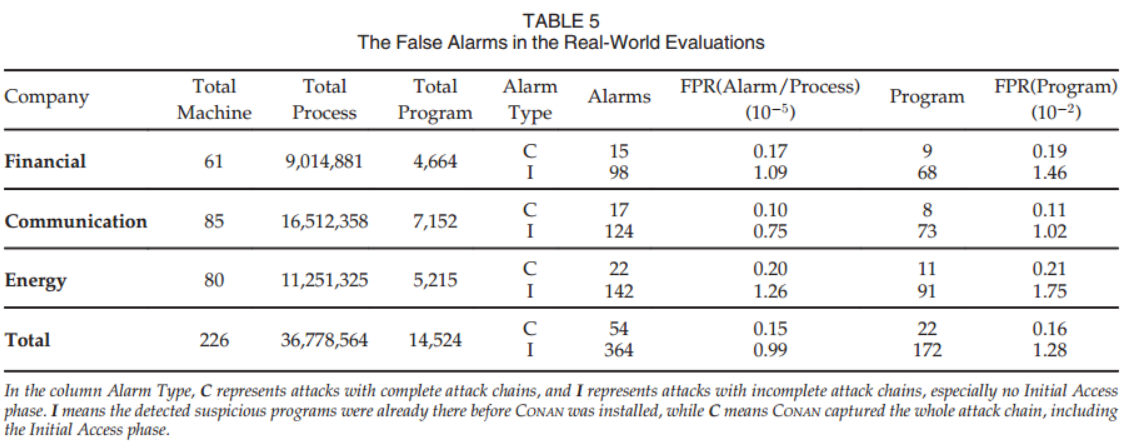
【论文阅读】CONAN:一种实用的、高精度、高效的APT实时检测系统(TDSC-2020)
CONAN:A Practical Real-Time APT Detection System With High Accuracy and Efficiency TDSC-2020 浙江大学 Xiong C, Zhu T, Dong W, et al. CONAN: A practical real-time APT detection system with high accuracy and efficiency[J]. IEEE Transactions on Dep…...
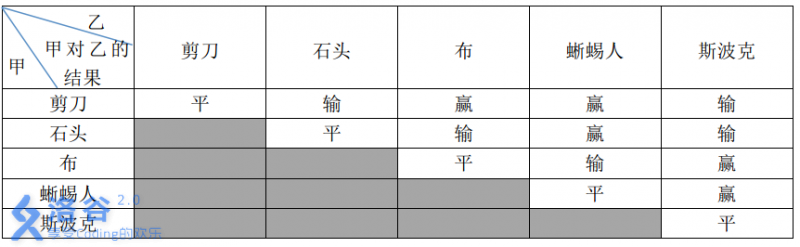
P1328 [NOIP2014 提高组] 生活大爆炸版石头剪刀布
题目描述 石头剪刀布是常见的猜拳游戏:石头胜剪刀,剪刀胜布,布胜石头。如果两个人出拳一样,则不分胜负。在《生活大爆炸》第二季第 8 集中出现了一种石头剪刀布的升级版游戏。 升级版游戏在传统的石头剪刀布游戏的基础上,增加了两个新手势: 斯波克:《星际迷航》主…...
基于Android水果蔬菜果蔬到家商城系统 微信小程序uniAPP的开发与实现
果蔬到家是商家针对用户必不可少的一个部分。在商铺发展的整个过程中,果蔬到家担负着最重要的角色。为满足如今日益复杂的管理需求,各类果蔬到家程序也在不断改进。本课题所设计的springboot基于HBuilder X的果蔬到家APP,使用SpringBoot框架&…...
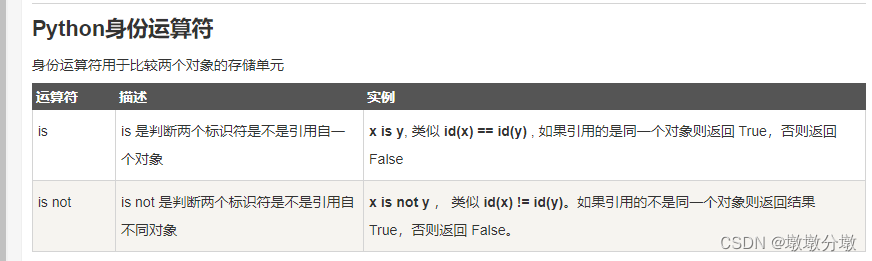
【Python】从入门到上头—Python基础(2)
文章目录 一.基础语法1.编码2.标识符3.保留字4.注释5.行与缩进6.多行语句7.数字(Number)类型8.字符串(String)9.空行10.等待用户输入11.同一行显示多条语句12.多个语句构成代码组13.print 输出14.import 与 from...import 二.基本数据类型1.变量和赋值2.多个变量赋值3.标准数据…...
leetcode刷题之283:移动零
问题 实现思路 首先, 将dest指向-1 位置, cur指向下标为0 的位置, 在cur遍历的过程中: 1) 遇到非零元素则与下标dest1 位置的元素交换, 2) 若遇到零元素则只继续cur遍历. 下标为1 的位置上是 非零元素 执行1) 交换得到右图结果 随后cur 得到下图结果 下标为2 的位置上是零…...

【Spring Boot】SpringBoot和数据库交互: 使用Spring Data JPA
文章目录 1. 数据库和Java应用程序1.1 为什么需要数据库交互1.2 传统的数据库交互方法 2. 什么是JPA2.1 JPA的定义2.2 JPA的优势 3. Spring Data JPA介绍3.1 Spring Data JPA的特性3.2 如何简化数据库操作 4. 在SpringBoot中集成Spring Data JPA4.1 添加依赖4.2 配置数据源 5. …...
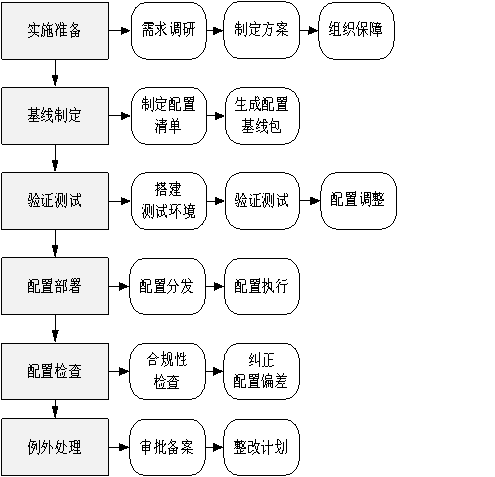
自动化部署及监测平台基本架构
声明 本文是学习 政务计算机终端核心配置规范. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 核心配置自动化部署及监测技术要求 自动化部署及监测平台基本架构 对于有一定规模的政务终端核心配置应用,需要配备自动化部署及监测平台&am…...
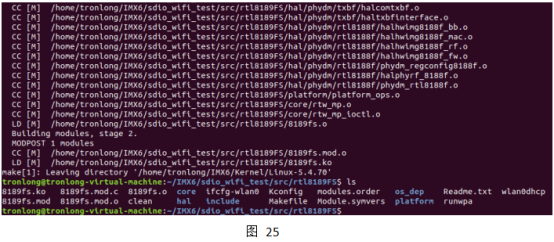
基于NXP i.MX 6ULL核心板的物联网模块开发案例(1)
目录 前 言 1 SDIO WIFI模块测试 1.1 STA模式测试 1.2 AP模式测试 1.3 SDIO WIFI驱动编译 前言 本文主要介绍基于创龙科技TLIMX6U-EVM评估板的物联网模块开发案例,适用开发环境: Windows开发环境:Windows 7 64bit、Windows 10 64bit …...
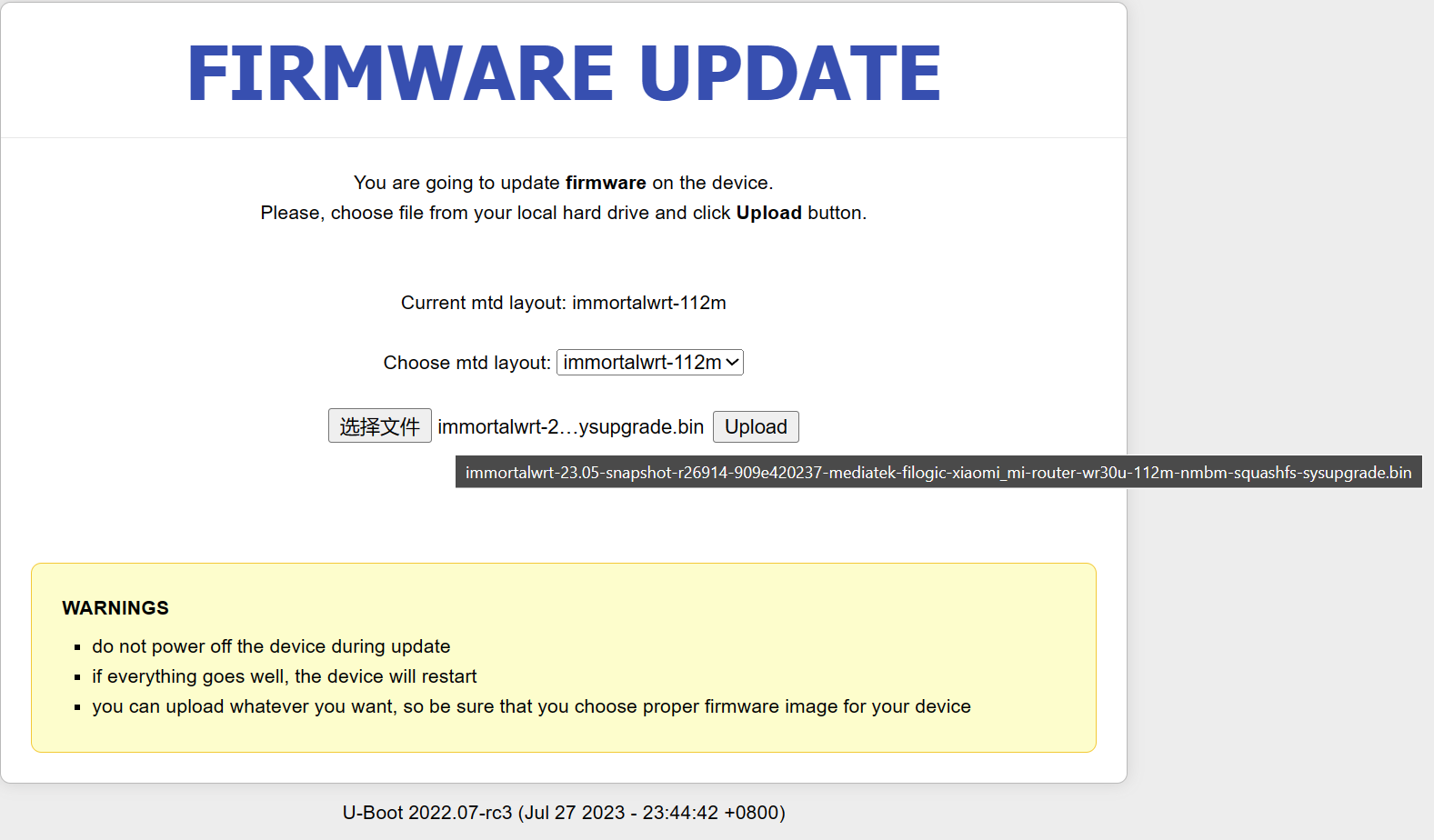
【路由器】小米 WR30U 解锁并刷机
文章目录 解锁 ssh环境准备解锁过程 刷入 mt798x uboot简介刷入流程 刷入 ImmortalWrt简介刷入流程 刷为原厂固件参考资料 本文主要记录个人对小米 WR30U 路由器的解锁和刷机过程,整体步骤与 一般安装流程 类似,但是由于 WR30U 的解锁 ssh 和刷机的过程中…...

数据库操作语句
一,SQL分类 DDL:数据定义语言 DML:数据操纵语言 DQL:数据查询语言 DCL:数据控制语言 创建数据库和表 #创建数据库 create database 数据库名; #创建数据表 create table 表名 (字段1 字段1类型(字段长度) 字段限制,字…...
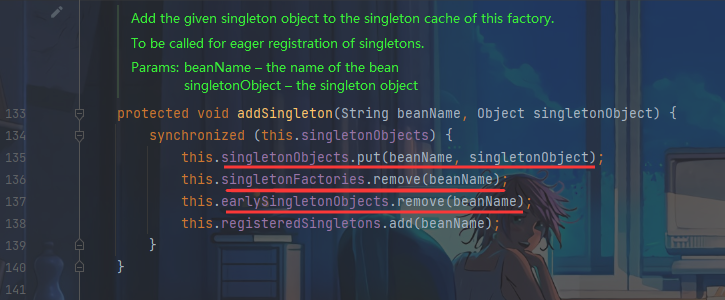
Mr. Cappuccino的第64杯咖啡——Spring循环依赖问题
Spring循环依赖问题 什么是循环依赖问题示例项目结构项目代码运行结果 Async注解导致的问题使用Lazy注解解决Async注解导致的问题开启Aop使用代理对象示例项目结构项目代码运行结果 Spring是如何解决循环依赖问题的原理源码解读 什么情况下Spring无法解决循环依赖问题 什么是循…...

Adapting Language Models to Compress Contexts
本文是LLM系列文章,针对《Adapting Language Models to Compress Contexts》的翻译。 使语言模型适应上下文压缩 摘要1 引言2 相关工作3 方法4 实验5 上下文学习6 压缩检索语料库实现高效推理7 结论不足 摘要 1 引言 2 相关工作 3 方法 4 实验 5 上下文学习 …...

Kubernetes(K8S)使用PV和PVC做存储安装mysql
Kubernetes使用PV和PVC做存储安装mysql 环境准备什么是PV和PVC环境准备配置nfs安装nfs配置nfs服务端 创建命名空间配置pv和pvcpv的yaml文件pvc的yaml文件 部署mysql创建mysql的root密码的secret创建mysql部署的yaml部署mysql链接mysql外部链接内部链接 环境准备 首先你需要一个…...

Ansible Playbook 常用变量
以下是 Ansible Playbook 常用变量 ansible_connection: 指定连接类型(如 ssh、winrm) ansible_user: 指定远程用户 ansible_ssh_pass: 指定远程用户密码 ansible_become: 指定是否切换为超级用户 ansible_become_user: 指定切换到的用户 ansible_b…...
0103水平分片-jdbc-shardingsphere-中间件
文章目录 1 准备服务器1.1 创建server-order0容器1.2 创建server-order1容器 2、基本水平分片2.1、基本配置2.2、数据源配置2.3、标椎分片表配置2.4、行表达式2.5、分片算法配置2.6、分布式序列算法 3、多表关联3.1、创建关联表3.2、创建实体类3.3、创建Mapper3.4、配置关联表3…...
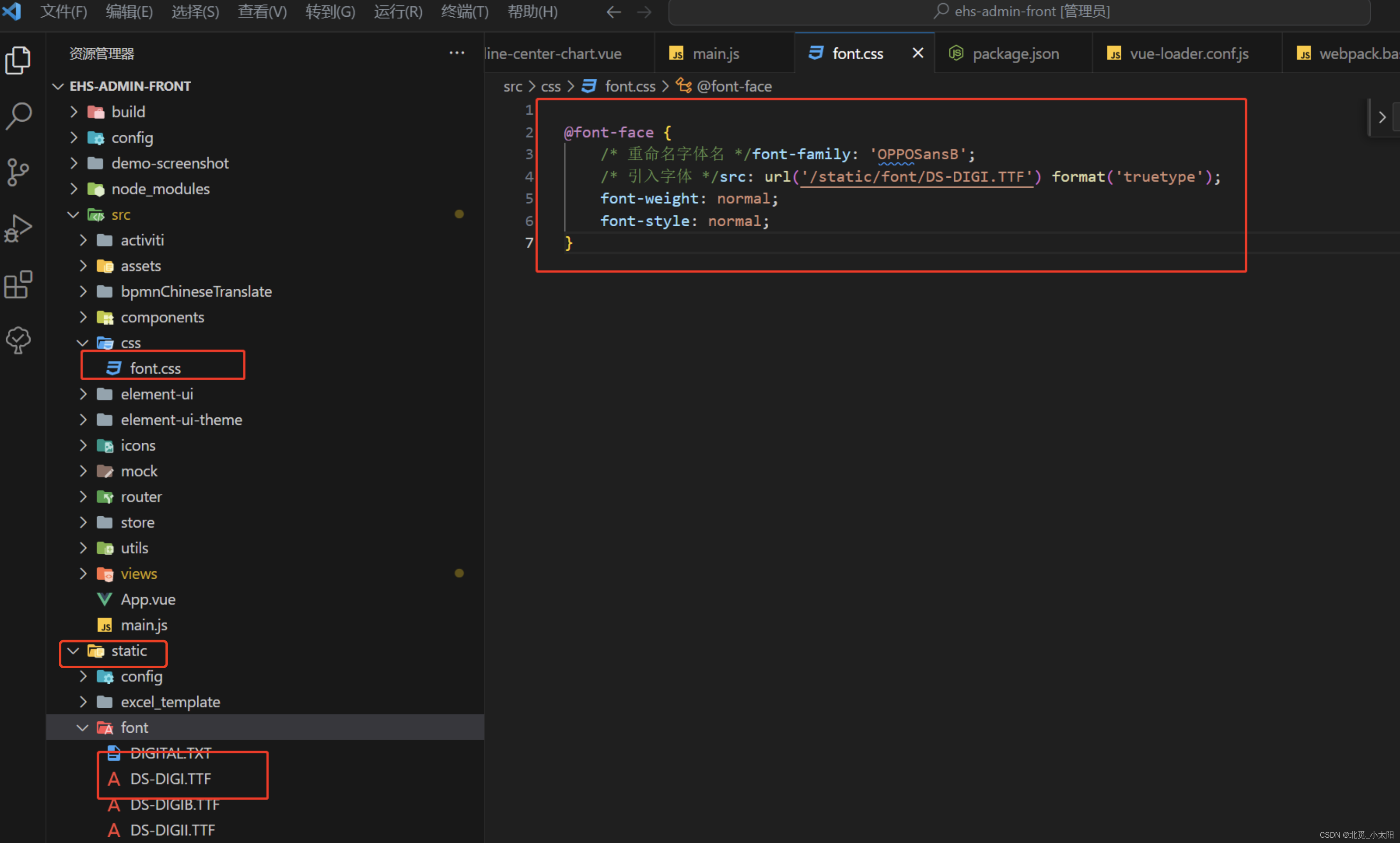
Vue2.0+webpack 引入字体文件(eot,ttf,woff)
webpack.base.config.js 需要配置 {test:/\/(woff2?|eot|ttf|otf)(\?.*)?$/,loader: url-loader,options: {limit: 10000,name: utils.assetsPath(fonts/[name].[hash:7].[ext])}} 如果 Vue2.0webpack3.6引入字体文件(eot,ttf,woff&…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

