Java【手撕双指针】LeetCode 57. “两数之和“, 图文详解思路分析 + 代码
文章目录
- 前言
- 一、两数之和
- 1, 题目
- 2, 思路分析
- 3, 代码展示
前言
各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你:
📕 JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等
📗 Java数据结构: 顺序表, 链表, 堆, 二叉树, 二叉搜索树, 哈希表等
📘 JavaEE初阶: 多线程, 网络编程, TCP/IP协议, HTTP协议, Tomcat, Servlet, Linux, JVM等(正在持续更新)
一、两数之和
1, 题目
OJ链接
题目给定的数组保证有序, 并且需求是查找
-
查找的本质是排除 ! ! 查找的本质是排除 ! ! 查找的本质是排除 ! !
-
有序的数组成单调性, 能很方便的使用双指针
2, 思路分析
最简单的暴力枚举 : 两层 for 循环, 从先固定一个数, 再依次遍历第二个数, 判断这两个数的和是否为 targer(目标值), 时间复杂度为O(N²), 会超出时间限制
既然暴力枚举不行, 那尝试就使用双指针
根据实际情况分析选择对撞双指针还是快慢双指针, 本题要求在数组中"查找", 那么使用对撞双指针能很大程度上提高效率
而且刚才标注了一句话 : 查找的本质是排除, 查找的本质是排除, 查找的本质是排除 ! ! !
如果每次判断, 都能尽可能多的排除数据, 就能尽可能地提高效率
解题步骤 :
- 定义 left 指针在 0 下标, 定义 right 指针在 nums.length - 1 下标
- left 的值 + right 的值, 和 target 比较
- 如果二者之和等于 target , 即为所求
- 如果二者之和大于 targer, 令 right-- (这一步就是在排除)
- 如果二者之和小于 targret, 令 left++ (这一步就是在排除)

如何理解利用数组单调性, 双指针能够高效的排除 ?
如果数组不是单调的, 不能保证 10 后面的数一定比 10 大, 就不能排除了
3, 代码展示
public int[] twoSum(int[] nums, int target) {int left = 0;int right = nums.length - 1;while(left < right) {if(nums[left] + nums[right] > target) {right--;}else if(nums[left] + nums[right] < target){left++;}else {return new int[]{nums[left],nums[right]};}}return nums;}
相关文章:

Java【手撕双指针】LeetCode 57. “两数之和“, 图文详解思路分析 + 代码
文章目录 前言一、两数之和1, 题目2, 思路分析3, 代码展示 前言 各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你: 📕 JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等 📗 Java数据结构: 顺序表, 链表…...

大数据(一)定义、特性
大数据(一)定义、特性 本文目录: 一、写在前面的话 二、大数据定义 三、大数据特性 3.1、大数据的大量 (Volume) 特性 3.2、大数据的高速(Velocity)特性 3.3、大数据的多样化 (Variety) 特性 3.4、大数据的价值 (value) 特性 3.5、大…...
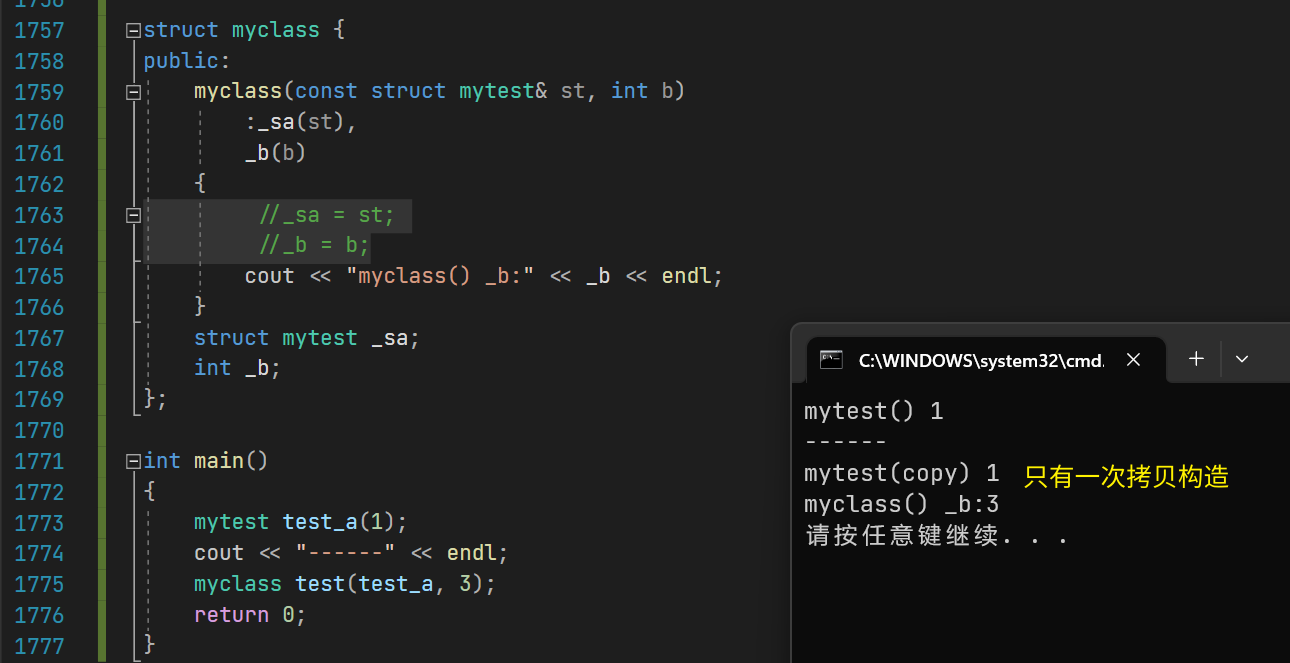
【C++】构造函数和初始化列表的性能差距
构造函数和初始化列表的性能差距对比测试 1.说明 在C类和对象中,你可能听到过更加推荐用初始化列表来初始化类内成员。如果类内成员是自定义类型,则只能在初始化列表中调用自定义类型的构造函数。 但初始化列表和在构造函数体内直接赋值有无性能差距呢…...

Linux下套接字TCP实现网络通信
Linux下套接字TCP实现网络通信 文章目录 Linux下套接字TCP实现网络通信1.引言2.具体实现2.1接口介绍1.socket()2.bind()3.listen()4.accept()5.connect() 2.2 服务器端server.hpp2.3服务端server.cc2.4客户端client.cc 1.引言 套接字(Socket)是计算机网络中实现网络通信的一…...

❤ vue清除定时器Bug
❤ vue清除定时器Bug 页面加载,清除定时器 clearTimeout(intm) 问题 遇见的需求是:webapp 从A页面进入B页面,B页面点击按钮,加载完B页面的加载效果进入c,从C页面返回A页面,仍然显示B页面的加载效果 结果定时器一直…...
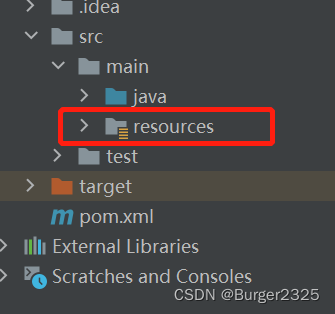
IDEA创建Spring,Maven项目没有resources文件夹
有时新建Spring或Maven项目时,会出现目录中main下无resources文件夹的情况,来一起解决一下: FIles|Project Structure 在Modules模块找到对应路径,在main下创建resources,右键main,选择新文件夹 输入文件…...
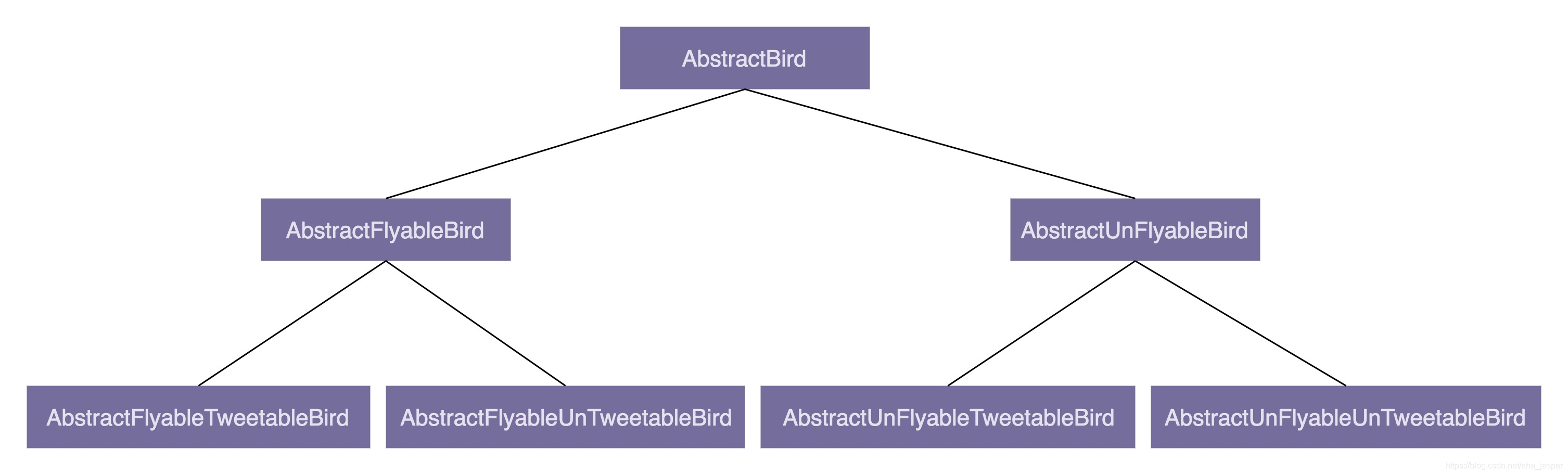
Unity 结构少继承多组合
为什么不推荐使用继承? 继承是面向对象的四大特性之一,用来表示类之间的 is-a 关系,可以解决代码复用的问题。虽然继承有诸多作用,但继承层次过深、过复杂,也会影响到代码的可维护性。所以,对于是否应该在…...

保研之旅2:中科院声学所“声学和信息学科”夏令营
💥💥💞💞欢迎来到本博客❤️❤️💥💥 本人持续分享更多关于电子通信专业内容以及嵌入式和单片机的知识,如果大家喜欢,别忘点个赞加个关注哦,让我们一起共同进步~ &#x…...

android adb自动连接手机安装apk bat
1.新建bat文件adb echo off:apk文件名称 在setting.txt获取 set apkFileName"":设置文件 set settingFileE:\apk\bat\setting.txt:启动页面 applicationid/启动页面路径 set startActivitycom.aaa.aaa/com.aaa.aaa.ui.common.SplashActivity:读取settingFile第一行的…...

用心维护好电脑,提高学习工作效率
无论是学习还是工作,电脑都是IT人必不可少的重要武器,一台好电脑除了自身配置要经得起考验,后期主人对它的维护也是决定它寿命的重要因素! 一、我的电脑 系统制造商: ASUSTeK COMPUTER INC. 系统型号: ZenBook UX481FAY 1.1 如…...

以太坊硬分叉后的可重入漏洞攻击
以太坊硬分叉后的可重入漏洞攻击 以太坊君士坦丁堡升级将降低部分 SSTORE 指令的 gas 费用。然而,这次升级也有一个副作用,在 Solidity 语言编写的智能合约中调用 address.transfer()函数或 address.send()函数时存在可重入漏洞。在目前版本的以太坊网络…...
k8s 常用命令(三)
1、查看版本信息:kubectl version [rootmaster ~]# kubectl version [rootmaster ~]# kubectl version Client Version: version.Info{Major:"1", Minor:"21", GitVersion:"v1.21.3", GitCommit:"ca643a4d1f7bfe34773c74f7952…...

API 网关基础
目录 一、网关概述二、网关提供的功能三、常见网关系统3.1 Netflix Zuul3.2 Spring Cloud Gateway3.3 Kong3.4 APISIX3.5 Shenyu 一、网关概述 API网关是一个服务器,是系统的唯一入口。 从面向对象设计的角度看,它与外观模式类似。API网关封装了系统内部…...

【Linux】权限问题
Linux权限 一、Linux 权限的概念二、Linux 权限管理1. 文件访问者的分类2. 文件类型和访问权限(事物属性)3. 文件访问权限的相关设置方法 三、默认权限1. 对文件和目录进行操作需要的权限2. 文件和目录的默认权限3. 粘滞位 一、Linux 权限的概念 Linux …...
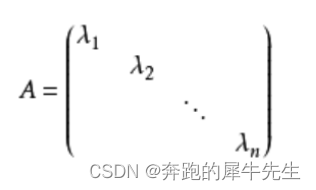
线性代数的学习和整理10:各种特殊类型的矩阵(草稿-----未完成 建设ing)
目录 1 图形化分类 1.1对称矩阵 1.2 梯形矩阵 1.3 三角矩阵 1.3.1 上三角矩阵 1.4 对角线矩阵 2 按各自功能分 2.1 等价矩阵 2.2 增广矩阵 2.3 伴随矩阵 2.4 正交矩阵 2.5 正交矩阵 2.6 相似矩阵 1 图形化分类 1.1对称矩阵 1.2 梯形矩阵 1.3 三角矩阵 1.3.1 上…...

Go 自学:变量、函数、结构体、接口、错误处理
1. 打印变量数据类型 package mainimport "fmt"func main() {penniesPerText : 2.0fmt.Printf("The type of penniesPerText is %T\n", penniesPerText) }输出为: The type of penniesPerText is float64 2. 同时给多个变量赋值 package mai…...

pyqt Pyton VTK 使用 滑块 改变 VTK Actor 颜色
使用 PyQt5 vtk vtk球体 使用滑块 RGB 改变 Actor 颜色 CODE import sys from PyQt5.QtWidgets import * from PyQt5.QtWidgets import (QApplication, QCheckBox, QGridLayout, QGroupBox,QMenu, QPushButton, QRadioButton, QVBoxLayout, QWidget, QSlider,QLineEdit,QLabe…...

春秋云镜 CVE-2019-16113
春秋云镜 CVE-2019-16113 Bludit目录穿越漏洞 靶标介绍 在Bludit<3.9.2的版本中,攻击者可以通过定制uuid值将文件上传到指定的路径,然后通过bl-kernel/ajax/upload-images.php远程执行任意代码。 启动场景 漏洞利用 exp https://github.com/Kenun…...

【JavaEE基础学习打卡06】JDBC之进阶学习PreparedStatement
目录 前言一、PreparedStatement是什么二、重点理解预编译三、PreparedStatement基本使用四、Statement和PreparedStatement比较1.PreparedStatement效率高2.PreparedStatement无需拼接参数3.PreparedStatement防止SQL注入 总结 前言 📜 本系列教程适用于JavaWeb初学…...

Postgresql12基于时间点恢复
1、环境 centos 7系统 postgresql 12 docker 20.10.6 2、整体思路 1)进行一个pgdata目录的全量备份 2)通过wal日志恢复到故障发生之前某个时间点 3、操作步骤 配置postgresql.conf文件 #日志级别 wal_level replica #归档开关 archive_mode on …...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
