CS224W课程学习笔记(三):DeepWalk算法原理与说明
引言
什么是图嵌入?
图嵌入(Graph Embedding,也叫Network Embedding) 是一种将图数据(通常为高维稠密的矩阵)映射为低微稠密向量的过程,能够很好地解决图数据难以高效输入机器学习算法的问题。以及图嵌入是将属性图转换为向量或向量集。嵌入应该捕获图的拓扑结构、顶点到顶点的关系以及关于图、子图和顶点的其他相关信息。更多的属性嵌入编码可以在以后的任务中获得更好的结果。
为什么要使用图嵌入(graph embedding)?
图是一种易于理解的表示形式,除此之外出于下面的原因需要对图进行嵌入表示:
- 在graph上直接进行机器学习具有一定的局限性, 我们都知道图是由节点和边构成,这些向量关系一般只能使用数学,统计或者特定的子集进行表示,但是嵌入之后的向量空间具有更加灵活和丰富的计算方式。
- 图嵌入能够压缩数据, 我们一般用邻接矩阵描述图中节点之间的连接。 连接矩阵的维度是∣V∣∗∣V∣|V| * |V|∣V∣∗∣V∣,其中∣V∣|V|∣V∣ 是图中节点的个数。矩阵中的每一列和每一行都代表一个节点。矩阵中的非零值表示两个节点已连接。将邻接矩阵用用大型图的特征空间几乎是不可能的。一个具有1M节点和1Mx1M的邻接矩阵的图该怎么表示和计算呢?但是嵌入可以看做是一种压缩技术,能够起到降维的作用。
- 向量计算比直接在图上操作更加的简单、快捷
参考:为什么要进行图嵌入(Graph embedding)?
课程链接与相关工具介绍
| 斯坦福原版视频 |
https://www.youtube.com/watch?v=rMq21iY61SE&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=7
https://www.youtube.com/watch?v=Xv0wRy66Big&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=8
https://www.youtube.com/watch?v=eliMLfJeu7A&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=9
https://www.youtube.com/watch?v=r12qJZZVtqc&list=PLoROMvodv4rPLKxIpqhjhPgdQy7imNkDn&index=13
| 本节课学习资料与工具 |
deepwalk论文地址:https://arxiv.org/pdf/1403.6652.pdf
node2vec论文地址:https://arxiv.org/pdf/1607.00653.pdf
deepwalk模型详解
deepwalk之前的方案说明
最开始的图嵌入算法,只是将NLP中其余方向上的指标直接运用于图,根据上面的Node2Vec论文中提到的,我这里列举三种方式。
1. 共同好友个数(Common neighbors):
∣N(v1)∩N(v2)∣∣N(v_1)∩N(v_2)∣∣N(v1)∩N(v2)∣
这个就如公式表达的那样,相当于两个圈子取了一个交集。
2. Jaccard’s coefficient(相似系数):
J(A,B)=∣A∩B∣∣A∪B∣=∣A∩B∣∣A∣+∣B∣−∣A∩B∣.J(A,B) = {{|A \cap B|}\over{|A \cup B|}} = {{|A \cap B|}\over{|A| + |B| - |A \cap B|}}.J(A,B)=∣A∪B∣∣A∩B∣=∣A∣+∣B∣−∣A∩B∣∣A∩B∣.
跟CN公式一样,也是如公式表达,可简单看成交并比。
3. Adamic -Adar index(亚当指数)
A(x,y)=∑u∈N(x)∩N(y)1log∣N(u)∣{\displaystyle A(x,y)=\sum _{u\in N(x)\cap N(y)}{\frac {1}{\log {|N(u)|}}}}A(x,y)=u∈N(x)∩N(y)∑log∣N(u)∣1
Adamic -Adar 指数是Lada Adamic和Eytan Adar于 2003 年引入的一种衡量指标,用于根据两个节点之间的共享链接数量来预测社交网络中的链接。它被定义为两个节点共享的邻居的反对数度中心性的总和。在哪里N(u){\displaystyle N(u)}N(u)是相邻节点的集合,即与少数节点之间共享的元素相比,在预测两个节点之间的连接时,具有非常大邻域的公共元素不太重要。(来自wiki:https://en.wikipedia.org/wiki/Adamic%E2%80%93Adar_index)
虽然这几种指标我没用过,但类比于我用过的 皮尔逊相关系数、卡方检验等,显然如果用一个简单公式去衡量一份数据的好坏,还是有失偏颇,这里node2vec的论文也给出了测试结果:

可以看到,相比于(bcd)栏用算法以及模型去做图嵌入的效果,差距是很大的,那么就引出了第一个模型——DeepWalk。
deepwalk算法说明
时间到了2014年,那是word2vec问世的第二年,Bryan Perozzi[1]创造性地提出了DeepWalk,将词嵌入的方法引入图嵌入,将图嵌入引入了一个新的时代,文章首图就是以该文章的截图,向作者致敬。DeepWalk提出了“随机游走”的思想,这个思想有点类似搜索算法中的DFS,从某一点出发,以深搜的方式获得一个节点序列。这个序列即可以用来描述节点。参照下图:

(参考:基于随机游走的图嵌入(Graph Embedding)方法)
依照图中的连边关系,从节点1开始,可能依次经过节点2,6,1,3. 能够经过这些节点的原因是因为相邻的两个节点之间彼此有连边。每个节点每次游走的概率为节点的出度分之一,以节点1为例,将以等概率游走至节点2、3、4、6节点。这个过程非常容易理解,但是为什么游走出来的节点序列就可以描述一个节点,我这里给出一种直观的解释是:在有限步数的游走下,从1个节点出发,能到达的节点是所有节点的一个子集;每个节点随机游走产生的子集是不同的,这些不同的子集就可以用于描述不同节点。
这里关于随机游走算法,我查了很多资料,发现有很复杂的,用最大似然估计去优化目标函数,或者从三维球体考虑,加入了一些求解公式,但我看论文原文也没搞这么多花里胡哨的东西啊,可能是后来改进的,这里还是依照论文中的思路,大概步骤为:
- 选择一个初始点作为当前点
- 在当前点附近随机选取一个新点
- 计算新点和当前点的目标函数值
- 如果新点的目标函数值小于当前点的目标函数值,则将新点作为当前点,否则保持当前点不变
- 重复上述步骤直到满足停止条件
那么可以写第一版伪代码为:
# 使用Python实现随机游走算法
import numpy as np# 定义目标函数,这里使用一个简单的二次函数作为例子
def f(x):return x**2# 定义初始点和停止条件,这里使用最大迭代次数作为停止条件
x0 = np.random.uniform(-10,10) # 随机生成一个初始点
max_iter = 100 # 最大迭代次数# 开始随机游走
x = x0 # 将初始点赋值给当前点
for i in range(max_iter):print(f"第{i+1}次迭代,当前点为{x:.4f},目标函数值为{f(x):.4f}")x_new = x + np.random.normal(0,1) # 在当前点附近随机生成一个新点,这里使用正态分布作为例子if f(x_new) < f(x): # 如果新点的目标函数值小于当前点的目标函数值,则更新当前点x = x_new
然后在这个基础上,加入各种改进方案,比如我参考中所提到的,论文中给出了一个参数 α\alphaα 可用于实现带概率返回原点的游走策略。即在游走长度未到达预定长度 LLL 的情况下(假设游走了 kkk 步,0≤k≤L0 \leq k \leq L0≤k≤L表示可发生在游走的任何时刻),第k+1k+1k+1 步将有一定的概率 α\alphaα 返回原点。这样以来有助于获得更多较短的序列,如下图,红色连接线表示在该步的游走返回了原点。

获得了节点序列后,DeepWalk的创新之处就是使用这个数据:
作者提出了节点共现频率和词汇共现频率相似的统计结果,并认为这种结果表明:游走的序列可以类比语料库中的句子,序列中的节点可以类比句子中的单词,词汇的共现情况,类似于随机游走序列中节点的共现情况。这个统计结果可能只是作者拍脑袋想出来的,但是确实work。
通过节点->单词、节点序列->句子这个转化,就可以将图上的Embedding问题转化为一系列节点在游走序列中共现的问题,此时直接用gensim里的Word2Vec包就可以完成训练.
根据上面所写的简单版本的随机游走,加上参考中作者所给出将数据调入Word2Vec包中的demo,基本就能复现一个mini版本的Deepwalk:
node_adj_list = {} # 节点连边关系
nodes = [] # 所有节点
walk_sequences = []
for node in node_pairs:# 对网络中每一个节点for i in num_walks:# 产生num_walks个游走walk_sequence = []for j in walk_length:# 每次游走walk_length步# random pick a selected_node in node_adj_list[node]walk_sequence.append(selected_node)walk_sequences.append(walk_sequence)
# 最终需要的是walk_sequences
# 可以将walk_sequences扔进word2vec训练
矩阵分解角度理解deepwalk
该种方式是通过同济子豪兄课上所提到的,但是我看原论文中并没有找到相关,所以这里引述一下。通过邻接矩阵分解ZTZ=AZ^T Z=AZTZ=A ,可得:
- 两个节点之间相连:节点向量的数量积是1,两个节点是相似的
- 两个节点之间不相连:节点向量的数量积是0,两个节点是不相似的
优化目标函数:
minZ∥A−ZTZ∥2\min _Z\left\|A-Z^T Z\right\|_2ZminA−ZTZ2
DeepWalk的矩阵分解形式的目标函数:
log(vol(G)(1T∑r=1T(D−1A)r)D−1)−logb\log \left(\operatorname{vol}(G)\left(\frac{1}{T} \sum_{r=1}^T\left(D^{-1} A\right)^r\right) D^{-1}\right)-\log blog(vol(G)(T1r=1∑T(D−1A)r)D−1)−logb

即如上图,其中,vol(G)=∑i∑jAij\displaystyle vol(G) = \sum_i \sum_j A_{ij}vol(G)=i∑j∑Aij表示连接个数的2倍,TTT 表示上下文滑窗宽度,T=∣NR(u)∣T=|N_R(u)|T=∣NR(u)∣,DDD是对角矩阵,rrr 表示邻接矩阵的幂,bbb表示负采样的样本数。
重点还是放在论文版本的deepwalk中。
deepwalk算法步骤(进一步)
DeepWalk算法步骤,根据论文原文中的解释 DeepWalk(G,w,d,γ,t)\text{DeepWalk}(G, w, d, \gamma, t)DeepWalk(G,w,d,γ,t),公式为:
Input: graph G(V,E)G(V,E)G(V,E)
window size www(左右窗口宽度)
embedding size ddd (Embedding维度)
walks per vertex rrr (每个节点作为起始节点生成随机游走的次数)
walk lengthttt (随机游走最大长度)
output: maxtrix of vertex representations Φ∈R∣V∣×d\Phi \in R^{|V| \times d}Φ∈R∣V∣×d
1:Initialization: Sample Φ\PhiΦ from U∣V∣×d\mathcal{U}^{|V| \times d}U∣V∣×d
2:Build a binary Tree TTT from VVV
3:for iii = 0 to rrr do
4: O=Shuffle(V)\mathcal{O} = \text{Shuffle}(V)O=Shuffle(V) (随机打乱节点顺序)
5: for each vi∈Ov_i \in \mathcal{O}vi∈O do (遍历graph中的每个点)
6: Wvi=RandomWalk(G,vi,t)\mathcal{W}_{v_i} = \text{RandomWalk}(G, v_i, t)Wvi=RandomWalk(G,vi,t) (生成一个随机游走序列)
7: SkipGram(Φ,Wvi,w)\text{SkipGram}(\Phi, \mathcal{W}_{v_i}, w)SkipGram(Φ,Wvi,w) (由中心节点Embedding预测周围节点,更新Embedding)
8: end for
9:end for
其中的skipGram算法公式为SkipGram(Φ,Wvi,w)\text{SkipGram}(\Phi, \mathcal{W}_{v_i}, w)SkipGram(Φ,Wvi,w),步骤为:
1: for each vi∈Wviv_i \in \mathcal{W}_{v_i}vi∈Wvi
2: for each uk∈Wvi[j−w,j+w]u_k \in \mathcal{W}_{v_i}[j-w, j+w]uk∈Wvi[j−w,j+w] do(遍历该节点周围窗口里的每个点)
3: J(Φ)=−logPr(uk∣Φ(vj))J(\Phi)=-\log \text{Pr}(u_k | \Phi(v_j))J(Φ)=−logPr(uk∣Φ(vj)) (计算损失函数)
4: Φ=Φ−α∗∂J∂Φ\displaystyle \Phi = \Phi - \alpha * \frac{\partial J}{\partial \Phi}Φ=Φ−α∗∂Φ∂J (梯度下降更新Embedding矩阵)
5: end for
6:end for
可能上述排版会有些乱,论文原文截图为:

那么现在就非常清晰了,整个算法脉络梳理完全,deepwalk其实并不复杂,只是后续通过各种策略对随机游走就行了改进,下面给出一篇对游走过程进行代码模拟以及可视化的一篇博文,然后关于skip Gram可以见下图,以及geeksforgeeks 将word2vec源码抽取出来模拟训练的源代码:
Skip Gram model流程图:

(来源:geeksforgeeks : Implement your own word2vec(skip-gram) model in Python)
random walk可视化图:

(来源:数据分析学习笔记(六)-- 随机漫步)
deepwalk代码实战
总结完了算法框架,参考B站同济子豪兄的demo——维基百科图词条图嵌入实战,这里需要先收集数据,采用网站是:
https://densitydesign.github.io/strumentalia-seealsology/
这里输入想要爬取的wiki词条,然后设置distance,默认为1,如果想爬得深点,就设置3、4。爬取过程如下,以知识图谱的方式,过程是可视化的:
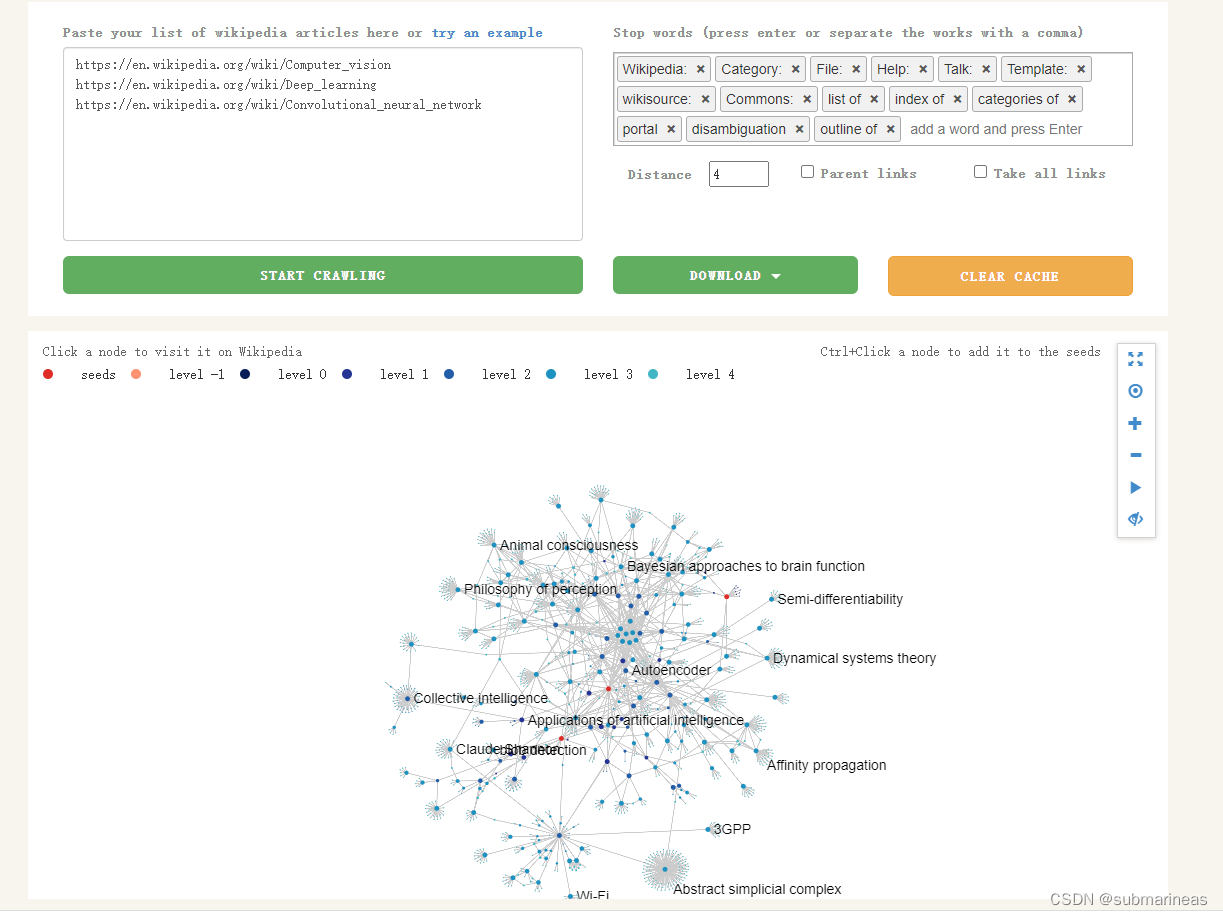
下载完数据后,首先导入必要的包,加载加载维基百科词条数据:
import networkx as nx
import pandas as pd
import numpy as np
import random
from tqdm import tqdmimport matplotlib.pyplot as plt
%matplotlib inlineplt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False df = pd.read_csv("seealsology-data.tsv", sep = "\t")
df.head()
| source | target | depth | |
|---|---|---|---|
| 0 | convolutional neural network | attention (machine learning) | 1 |
| 1 | convolutional neural network | convolution | 1 |
| 2 | convolutional neural network | deep learning | 1 |
| 3 | convolutional neural network | natural-language processing | 1 |
| 4 | convolutional neural network | neocognitron | 1 |
构建无向图,并转list方便游走:
# 构建无向图
G = nx.from_pandas_edgelist(df, "source", "target", edge_attr=True, create_using=nx.Graph())
all_nodes = list(G.nodes())
开始随机游走,构建序列:
# 生成随机游走节点序列的函数
def get_randomwalk(node, path_length):'''输入起始节点和路径长度,生成随机游走节点序列'''random_walk = [node]for i in range(path_length-1):# 汇总邻接节点temp = list(G.neighbors(node))temp = list(set(temp) - set(random_walk)) if len(temp) == 0:break# 从邻接节点中随机选择下一个节点random_node = random.choice(temp)random_walk.append(random_node)node = random_nodereturn random_walk# 每个节点作为起始点生成随机游走序列个数
gamma = 10
# 随机游走序列最大长度
walk_length = 5 # 生成随机游走序列
random_walks = []for n in tqdm(all_nodes):# 将每个节点作为起始点生成gamma个随机游走序列for i in range(gamma): random_walks.append(get_randomwalk(n, walk_length))
然后可查看全部的游走序列以及长度:
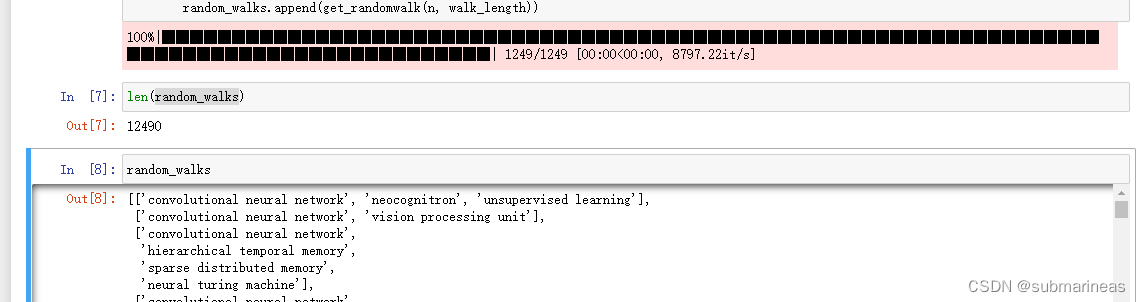
有了序列后,就可以接轨skipGram,也就是word2vec,具体代码为:
# 导入自然语言处理包
from gensim.models import Word2Vecmodel = Word2Vec(vector_size=256, # Embedding维数window=4, # 窗口宽度sg=1, # Skip-Gramhs=0, # 不加分层softmaxnegative=10, # 负采样alpha=0.03, # 初始学习率min_alpha=0.0007, # 最小学习率seed=14 # 随机数种子
)# 用随机游走序列构建词汇表
model.build_vocab(random_walks, progress_per=2)# 训练Word2Vec模型
model.train(random_walks, total_examples=model.corpus_count, epochs=50, report_delay=1)"""
(2003596, 2244800)
"""
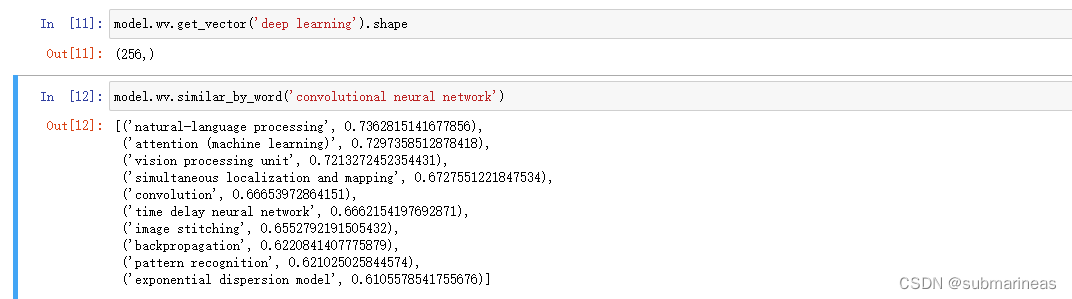
查看某个节点的Embedding:
model.wv.get_vector('deep learning').shape
"""
(256,)
"""
找相似词语:
# 找相似词语
model.wv.similar_by_word('convolutional neural network')
"""
[('natural-language processing', 0.7362815141677856),('attention (machine learning)', 0.7297358512878418),('vision processing unit', 0.7213272452354431),('simultaneous localization and mapping', 0.6727551221847534),('convolution', 0.66653972864151),('time delay neural network', 0.6662154197692871),('image stitching', 0.6552792191505432),('backpropagation', 0.6220841407775879),('pattern recognition', 0.621025025844574),('exponential dispersion model', 0.6105578541755676)]
"""
deepwalk模型增量训练
这里参考:word2vec模型训练保存加载及简单使用
首先我们可以根据上节跑出来的模型进行保存,这里跟我理解的其它机器学习模型一样,有三种保存方式:
# 方式一
model.save('word2vec.model')# 方式二
model2.wv.save_word2vec_format('word2vec.vector')
model2.wv.save_word2vec_format('word2vec.bin')
注意使用的API不同,一个是model.save() 一个是 model.wv.save_word2vec_format()。结果如图:.vector和.bin文件直接可以用txt打开可视,它们的内存占用要少一些,加载的时间要多一点。(PS:可以类比pytorch中的只保存参数,和整个模型)
保存了模型后,我又去加了两个新词条,一个是SVM,一个是决策树,这里再次进行爬取:
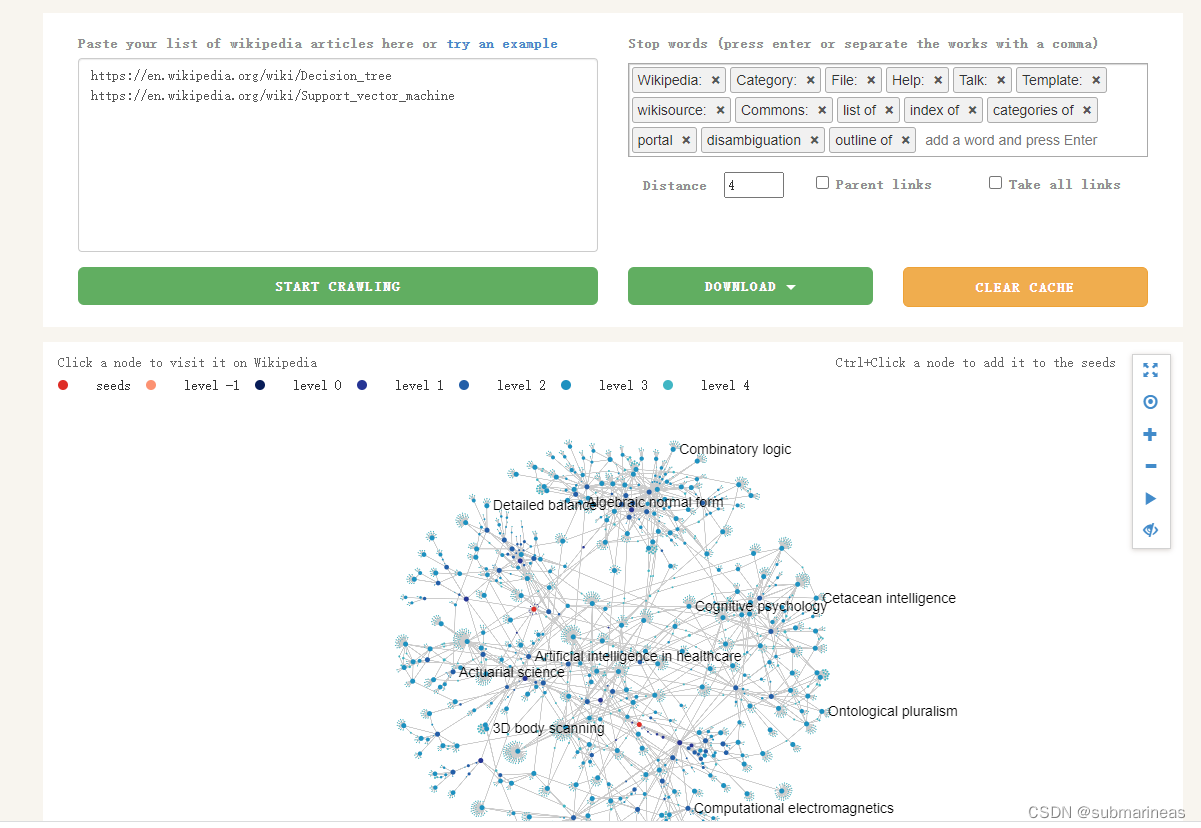
然后剩下过程基本一致,重新加载数据,重跑deepwalk构造序列,然后进行增量训练,这里不再演示,具体代码为:
model = Word2Vec.load('deepwalk.model')# deepwalk ——> data:random_walks#增量训练word2vec
model.build_vocab(random_walks,update=True) #注意update = True 这个参数很重要
model.train(random_walks,total_examples=model.corpus_count,epochs=10)
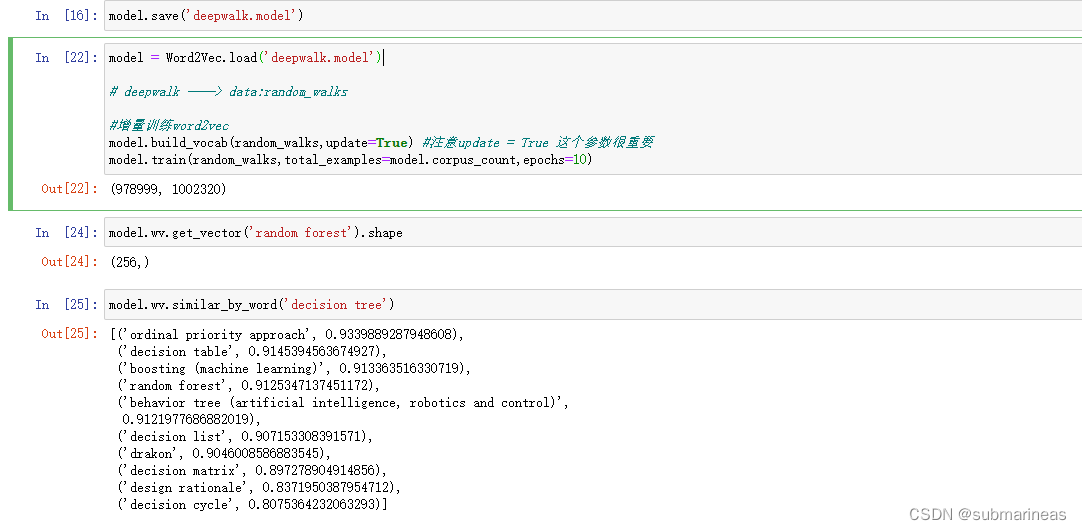
可以看到,决策树与支持向量机的序列就加入进原deepwalk.model中了。
deepwalk降维可视化
上面已经训练了word2vec模型,而model.wv.vectors是DeepWalk算法中使用Skip-gram模型训练后得到的词向量矩阵,每一行对应一个节点的向量表示。这些向量可以用于后续的图分析任务,如节点分类、聚类、相似度计算等。
PCA降维
这里直接给出代码为:
X = model.wv.vectors# 将Embedding用PCA降维到2维
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
embed_2d = pca.fit_transform(X)plt.figure(figsize=(10,10))
plt.scatter(embed_2d[:, 0], embed_2d[:, 1])
plt.show()

# 计算PageRank重要度
pagerank = nx.pagerank(G)
# 从高到低排序
node_importance = sorted(pagerank.items(), key=lambda x:x[1], reverse=True)# 取最高的前n个节点
n = 30
terms_chosen = []
for each in node_importance[:n]:terms_chosen.append(each[0])# 输入词条,输出词典中的索引号
term2index = model.wv.key_to_index# 可视化全部词条和关键词条的二维Embedding
plt.figure(figsize=(10,10))
plt.scatter(embed_2d[:,0], embed_2d[:,1])for item in terms_chosen:idx = term2index[item]plt.scatter(embed_2d[idx,0], embed_2d[idx,1],c='r',s=50)plt.annotate(item, xy=(embed_2d[idx,0], embed_2d[idx,1]),c='k',fontsize=12)
plt.show()

TSNE降维
t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法,是由 Laurens van der Maaten 等在08年提出来。此外,t-SNE 是一种非线性降维算法,非常适用于高维数据降维到2维或者3维,进行可视化。该算法可以将对于较大相似度的点,t分布在低维空间中的距离需要稍小一点;而对于低相似度的点,t分布在低维空间中的距离需要更远。
t-SNE的梯度更新有两大优势:
- 对于不相似的点,用一个较小的距离会产生较大的梯度来让这些点排斥开来。
- 这种排斥又不会无限大(梯度中分母),避免不相似的点距离太远。
劣势好像有点多,所以就不再转述,直接加进最后的参考与推荐了。这里我觉得PCA和TSNE的主要区别为:
- PCA是一种线性降维方法,它通过找到数据的最大方差方向来保留最多的信息,但它不能解释特征之间的非线性关系。
- TSNE是一种非线性降维方法,它通过计算高维和低维空间中的相似度来保留数据的局部结构,但它对参数的选择敏感,并且计算复杂度高。
那直接来看代码,为:
# 将Embedding用TSNE降维到2维
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, n_iter=1000)
embed_2d = tsne.fit_transform(X)plt.figure(figsize=(10,10))
plt.scatter(embed_2d[:,0], embed_2d[:,1])for item in terms_chosen:idx = term2index[item]plt.scatter(embed_2d[idx,0], embed_2d[idx,1],c='r',s=50)plt.annotate(item, xy=(embed_2d[idx,0], embed_2d[idx,1]),c='k',fontsize=12)
plt.show()

看起来区别还是挺大的,不过由于篇幅问题,这里就不再细研究了,之后有机会,再开一帖总结一下降维方法。
参考与推荐
[1]. https://densitydesign.github.io/strumentalia-seealsology/
[2]. 介绍一个全局最优化的方法:随机游走算法(Random Walk)
[3]. R语言: 聚类算法之PCA与tSNE
[4]. python: 最强降维模型t-SNE vs 最常用降维模型PCA(上)
[5]. Task05 DeepWalk论文精读
[6]. Markdown怎么首行缩进2格?
[7]. t-SNE:最好的降维方法之一
其余参考或者比较好玩的网站都在文中直接或间接给出,就不再这里引述
相关文章:

CS224W课程学习笔记(三):DeepWalk算法原理与说明
引言 什么是图嵌入? 图嵌入(Graph Embedding,也叫Network Embedding) 是一种将图数据(通常为高维稠密的矩阵)映射为低微稠密向量的过程,能够很好地解决图数据难以高效输入机器学习算法的问题。…...

rk3568 开发板Ubuntu系统说明
Ubuntu MinimalUbuntu Minimal系统基于Ubuntu 64bit系统构建,目前发布有Ubuntu18.04这个版本。与Ubuntu Desktop 相比具有以下特性:没有桌面环境,占用资源少,在简化网络管理之后,只需40M内存;针对嵌入式平台…...

Windows和Linux常用HASH算法使用命令
Windows和Linux常用hash算法使用命令 Windows,以文件xxx.zip为例 Windows 求文件 md5 certutil -hashfile xxx.zip md5Windows 求文件 sha1 certutil -hashfile xxx.zip sha1Windows 求文件 sha256 certutil -hashfile xxx.zip sha256Linux,以文件xxx.z…...
货仓选址 AcWing(JAVA)
在一条数轴上有 N家商店,它们的坐标分别为 A1∼AN。 现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送商品。 为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。 输入格式&#…...

SPI+DMA传输性能比较
本文章仅仅简单记录32单片机的SPIDMA驱动显示屏的性能测试,这里不花费时间介绍SPI和DMA。 硬件材料:SPI显示屏一个,32单片机 软件材料: 1.LCD的SPI驱动显示程序(SPI / SPIDMA): (1&a…...
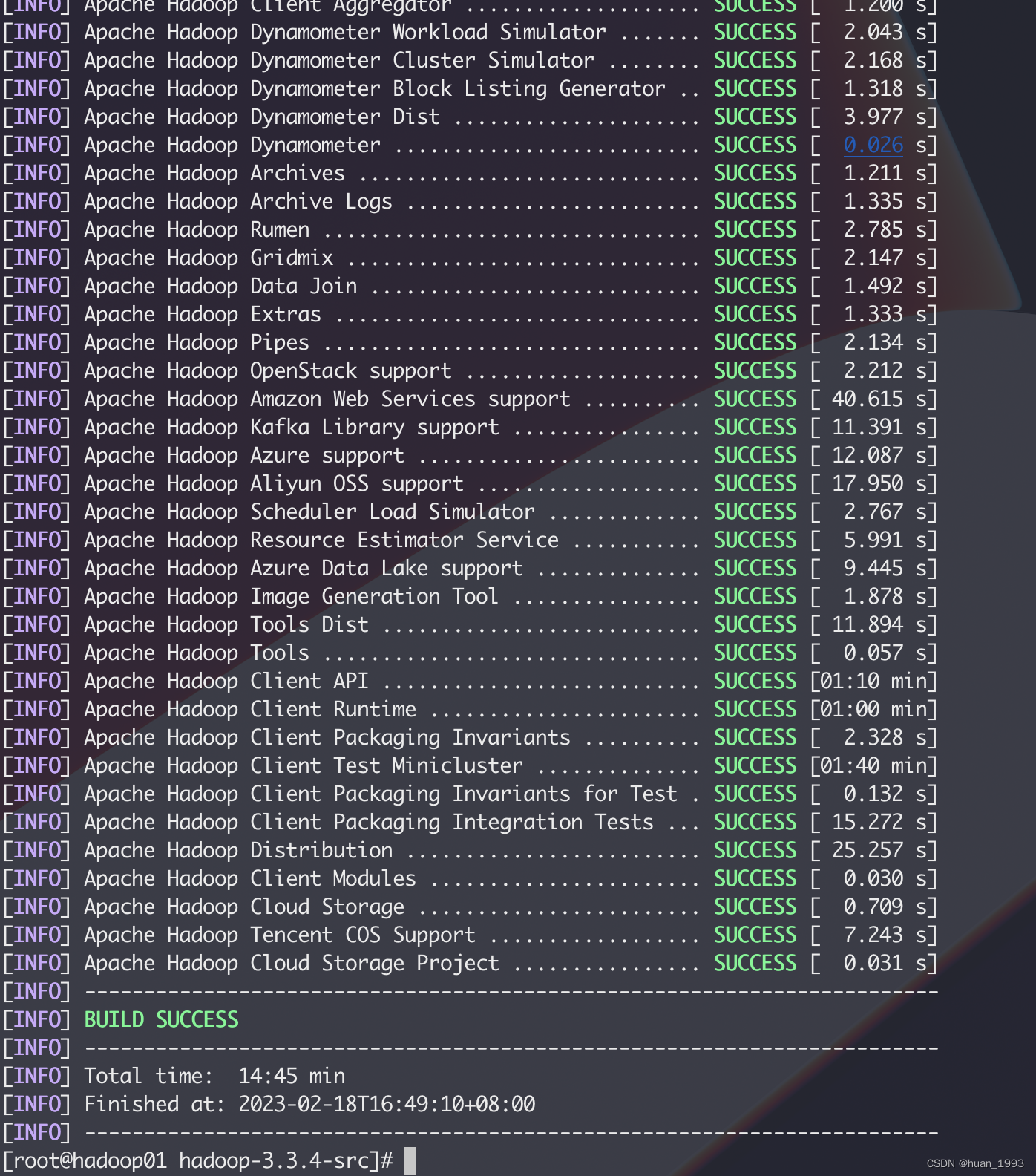
Centos7系统编译Hadoop3.3.4
1、背景 最近在学习hadoop,此篇文章简单记录一下通过源码来编译hadoop。为什么要重新编译hadoop源码,是因为为了匹配不同操作系统的本地库环境。 2、编译源码 2.1 下载并解压源码 [roothadoop01 ~]# mkdir /opt/hadoop [roothadoop01 ~]# cd /opt/had…...

pb并发控制
并发控制(一) 并发能力是指多用户在同一时间对相同数据同时访问的能力。一般的关系型数据库都具 有并发控制的能力,但是这种并发功能也会对数据的一致性带来危险。试想若有两个用 户都试图访问某个银行用户的记录并同时要求修改该用户的存款余额时,情况将会怎样 呢?我们可以…...

登录拦截器
文章目录前言一、interceptor1.interceptor 包下新建loginInterceptor.java2.config 包下新建 AdminWebConfig.java3.返回登录页面接收提示信息前言 本篇主要介绍spring框架里提供的 HandlerInterceptor 拦截器做登录拦截。 一、interceptor 1.interceptor 包下新建loginInte…...

STM32 - HAL库UART串口
1.串口初始化配置/******************************************************************************* Function: BSP_UART_Init Description: 串口初始化 Input: instance 串口号baudRate: 波特率 Output: 无 Return: 无 ************************************************…...
)
Vue3 的状态管理库(Pinia)
目录前言:一、什么是 Pinai二、安装与使用pinia三、什么是 store四、state1. 定义 state2. 组件中访问 state五、Getters1. 定义 Getters2. 在组件中使用 Getters六、Actions1. 定义Actions2. 组件中访问 Actions总结:前言: 在编写vue里的项目…...
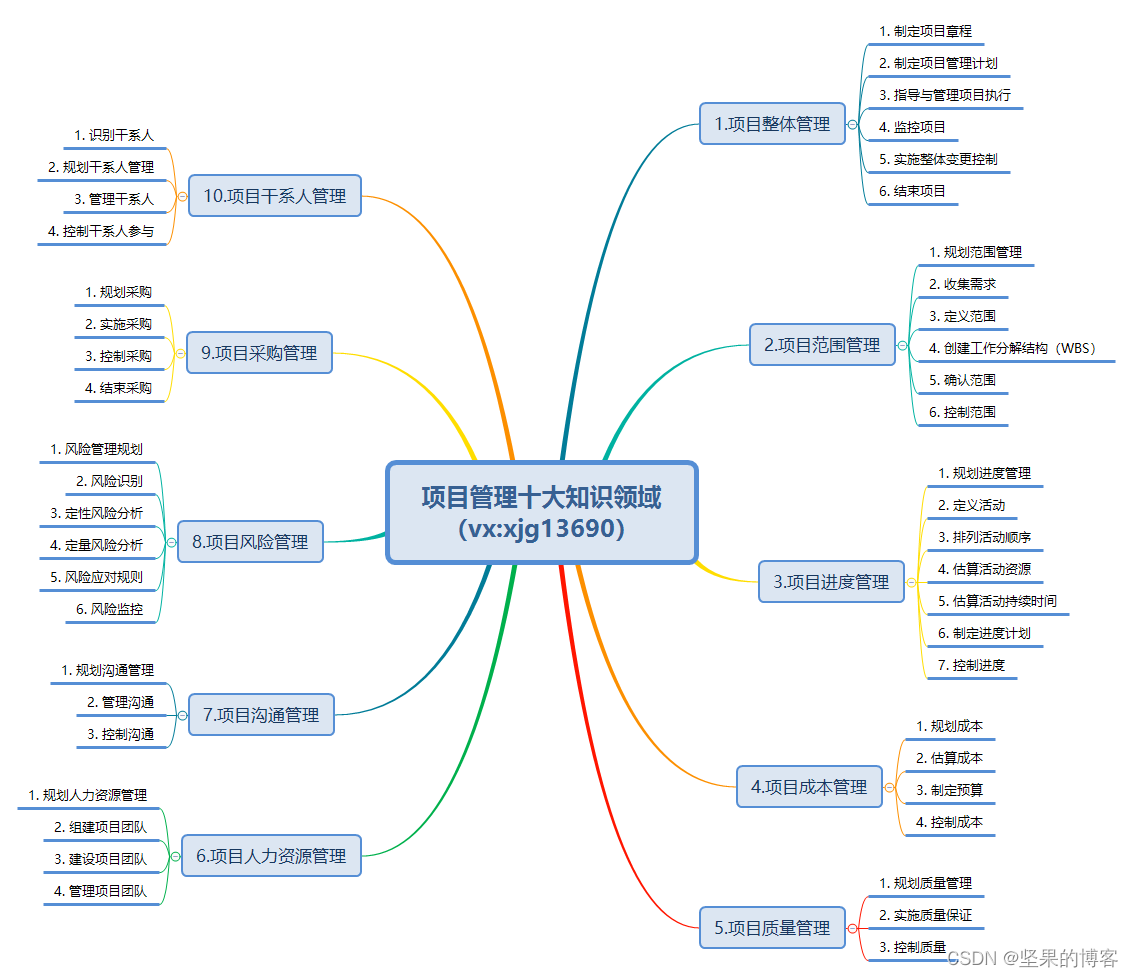
信息系统项目管理师知识点汇总(2023最新)
信息系统项目管理师 信息系统项目管理师简介如何应对考试考试细节与学习 十大管理 十大管理四十七过程 信息化和信息系统 项目管理基础 项目整体管理 项目范围管理 项目进度管理 项目成本管理 项目质量管理 项目人力资源管理 项目沟通管理 项目干系人管理 项目风险…...
标题标题标题
图床(Typora uPic/PicGo 七牛云) 图床(Typora uPic/PicGo 七牛云) 笔者平时使用 Typora 编写 markdown 文档,文档中常常会放置图片,如果文档不需要分享的话,其实讲图片存放在本地就可以了…...

OKR学习总结二
总结 绩效管理不是进行事后管理,而是参与整个过程并进行实时把控。 我们将受益目标分为两个子目标: 新增收入和重复收入。第一部分目标由市场营销部承担,第二个目标则由产品部承担。 简而言之,文化是一系列价值观和信仰的体现&…...
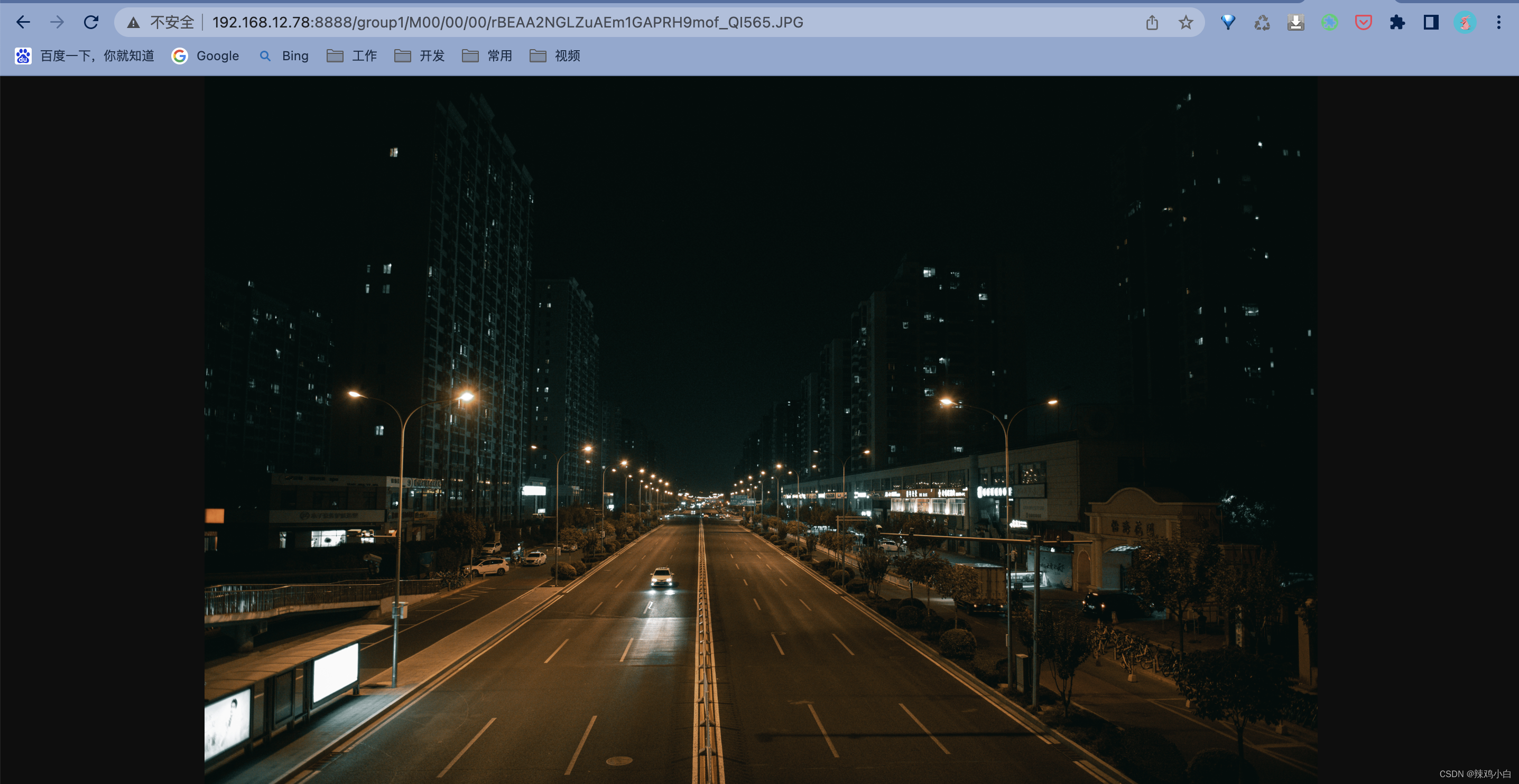
MAC中docker搭建fastdfs
1:首先搭建Docker2:通过Docker搭建fastdfs(1)查找镜像打开终端通命令查找fastdfs的镜像docker search fastdfs(二)拉取镜像在找到合适的镜像后执行命令:docker pull delron/fastdfs(三) 创建storage和track…...

JavaScript 变量
变量是用于存储信息的"容器"。实例var x5;var y6;var zxy;尝试一下 就像代数那样x5y6zxy在代数中,我们使用字母(比如 x)来保存值(比如 5)。通过上面的表达式 zxy,我们能够计算出 z 的值为 11。在…...

【前端验证】环境仿真中对于寄存器配置的随机策略讨论
前言 本篇文章旨在讨论环境仿真中对于寄存器配置的随机。 寄存器域的随机性 使用ralgen生成的寄存器本身是rand属性的,也就是说其自身是可以通过约束随机的方式在用例中进行随机性配置的,比如下面这个寄存器: class ral_reg_REG_PRJ_sys_cfg_base_config extends uvm_re…...

Servlet如何读取Web资源文件?【操作演示】
在实际开发中,有时候可能会需要读取Web应用中的一些资源文件,比如配置文件,图片等。为此,在ServletContext接口中定义了一些读取Web资源的方法,这些方法是依靠Servlet容器来实现的。Servlet容器根据资源文件相对于Web应…...
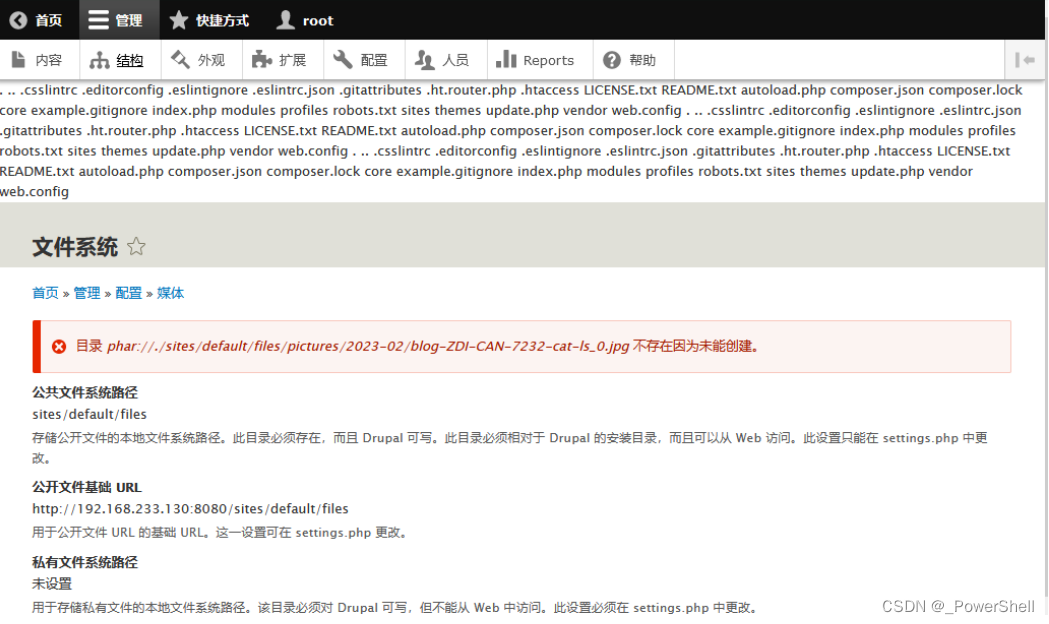
[ vulhub漏洞复现篇 ] Drupal 远程代码执行漏洞(CVE-2019-6339)
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

flex-shrink和felx-grow
本文就是简单的介绍下flex-shrink和felx-grow的作用和计算方式吧;关于这个介绍也是很多;flex-shrinkflex-shrink是flex布局中的一种方式,简单来说,就是当布局大小小于容器大小的时候,使用flex-shrink能够按照一定的比例…...
将HTTP接口配置成HTTPS
一、使用Java的keytool.exe程序生成本机的TLS许可找到Java的jdk目录进入bin默认安装路径C:\Program Files\Java\jdk1.8.0_91\bin 进入命令面板,在bin的路径栏中输入cmd敲击回车即可使用keytoolkeytool -genkeypair -alias tomcat_https -keypass 123456 -keyalg RSA…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...

Java设计模式:责任链模式
一、什么是责任链模式? 责任链模式(Chain of Responsibility Pattern) 是一种 行为型设计模式,它通过将请求沿着一条处理链传递,直到某个对象处理它为止。这种模式的核心思想是 解耦请求的发送者和接收者,…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...
