使用Python批量将飞书文档转为MD
说明:飞书是在线文档平台,本文介绍如何使用Python程序批量将飞书文档转为MD文档,并下载到本地;
复制地址
首先,把文档的URL都复制下来,这个需要一个一个点,并复制拷贝,但却是工作量最大的一步;

如下:
转换
飞书转为Markdown,在GitHub上有一个工具,可以在线将飞书的文档转为Markdown,并生成一个压缩包(.zip)到本地。
该工具,提供了一个在线版;
把前面飞书中的文档地址拷贝到这里,点DOWNLOAD就可以了。
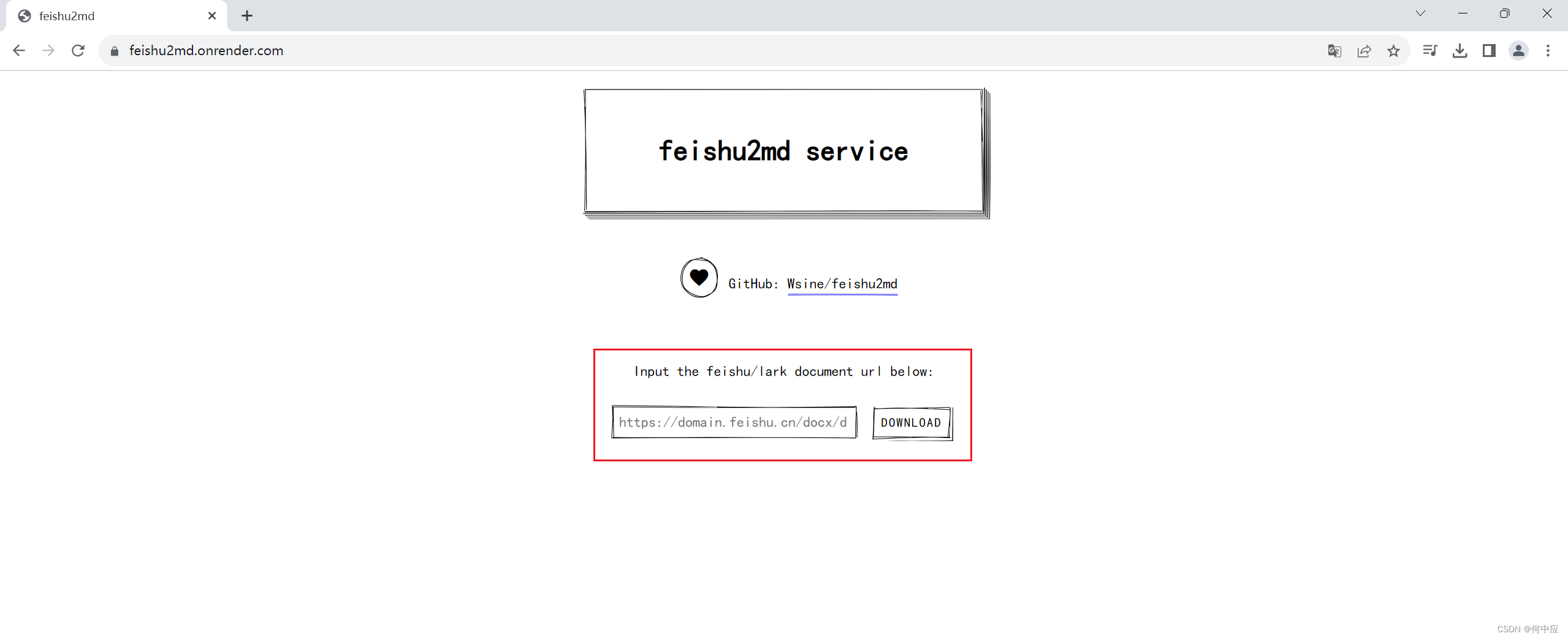
分析
我们可以通过Python程序,将需要转为MarkDown的飞书文档,使用Python程序循环去访问这个地址就好了。
首先,分析前面转换攻击,点击DOWNLOAD后发送的请求链接,如下:

通过分析,可知,地址的格式是这样的;
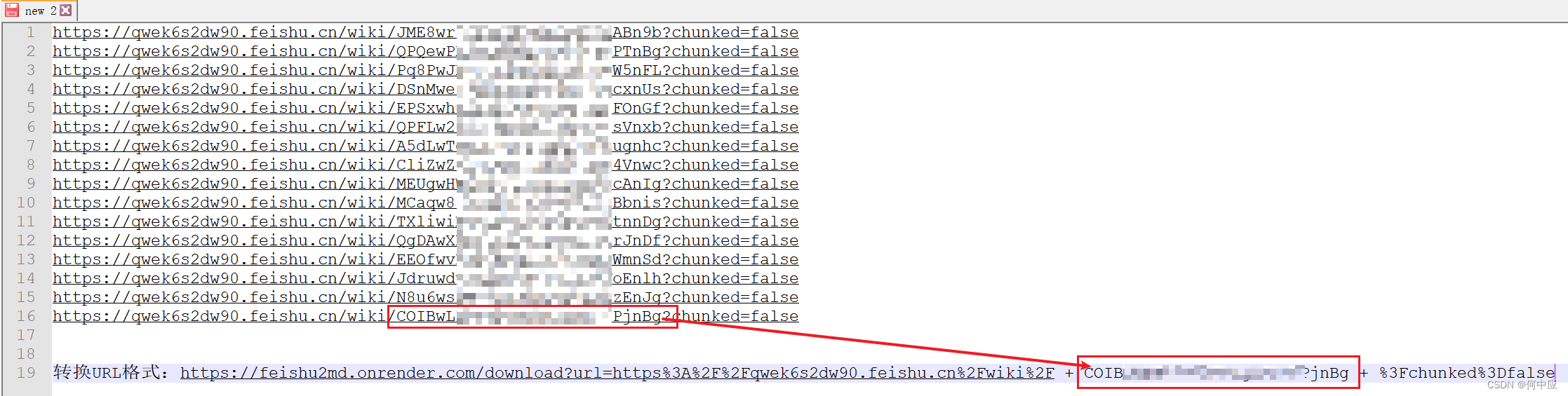
格式:
https://feishu2md.onrender.com/download?url=https%3A%2F%2Fqwek6s2dw90.feishu.cn%2Fwiki%2F + 文档地址码 + %3Fchunked%3Dfalse
编码
这就好办了,开始编码,如下:
import requests# 飞书中的文档地址码
doc_list = ["XXXXXXXXXXXXXXXXXXBn9b","XXXXXXXXXXXXXXXXXXTnBg","XXXXXXXXXXXXXXXXXX5nFL","XXXXXXXXXXXXXXXXXXxnUs","XXXXXXXXXXXXXXXXXXOnGf","XXXXXXXXXXXXXXXXXXVnxb","XXXXXXXXXXXXXXXXXXgnhc","XXXXXXXXXXXXXXXXXXVnwc","XXXXXXXXXXXXXXXXXXAnIg","XXXXXXXXXXXXXXXXXXbnis","XXXXXXXXXXXXXXXXXXnnDg","XXXXXXXXXXXXXXXXXXJnDf","XXXXXXXXXXXXXXXXXXmnSd","XXXXXXXXXXXXXXXXXXEnlh","XXXXXXXXXXXXXXXXXXEnJg","XXXXXXXXXXXXXXXXXXjnBg",
]# 遍历文档并转换
for index, value in enumerate(doc_list):# 拼接URLurl = ("https://feishu2md.onrender.com/download?url=https%3A%2F%2Fqwek6s2dw90.feishu.cn%2Fwiki%2F"+ value+ "%3Fchunked%3Dfalse")# 发送请求response = requests.get(url, stream=True)# 写入到本地if response.status_code == 200:with open(r'C:\Users\10765\Desktop\markdown'+ '\\' + str(index) + ".zip", "wb") as f:for chunk in response.iter_content(chunk_size=8192):f.write(chunk)print("文件下载完成!")else:print("文件下载失败,状态码:", response.status_code)
设置路径为桌面,文件名为索引,启动程序,测试,下载速度取决于飞鸽文档的大小,我这十几个文档,十分钟左右都下载完成了;
压缩包中包含文档和静态资源(图片);
这样,批量将飞书文档转为MD文档的步骤就完成了;
相关文章:

使用Python批量将飞书文档转为MD
说明:飞书是在线文档平台,本文介绍如何使用Python程序批量将飞书文档转为MD文档,并下载到本地; 复制地址 首先,把文档的URL都复制下来,这个需要一个一个点,并复制拷贝,但却是工作量…...
Nacos配置管理、Feign远程调用、Gateway服务网关
1.Nacos配置管理 1.1.将配置交给Nacos管理的步骤 1.在Nacos中添加配置 Data Id服务名称-环境名称.yaml eg:userservice-dev.yaml 2.引入nacos-config依赖 在user-service服务中,引入nacos-config的客户端依赖 <!--nacos配置管理依赖--> <dep…...

解决Spring Boot前后端分离开发模式中的跨域问题
在实际开发中,经常会遇到前端Vue应用与后端Spring Boot API接口存在跨域访问的问题。本篇博客将分享解决Spring Boot前端Vue跨域问题的实战经验,帮助开发者快速解决该问题。 一、跨域问题的原因 跨域问题是由于浏览器的同源策略引起的。同源策略限制了…...

常见前端面试之VUE面试题汇总五
13. assets 和 static 的区别 相同点: assets 和 static 两个都是存放静态资源文件。项目中所 需要的资源文件图片,字体图标,样式文件等都可以放在这两个文件 下,这是相同点 不相同点:assets 中存放的静态资源文件在…...

带着问题看SpringBoot
带着问题看SpringBoot 1、Spring容器具体是什么? 跟进run方法,context this.createApplicationContext(),得出容器是AnnotationConfigServletWebServerApplicationContext类。 SpringApplication.run(ServeroneApplication.class, args);…...

【Go 基础篇】Go语言匿名函数详解:灵活的函数表达式与闭包
介绍 在Go语言中,函数是一等公民,这意味着函数可以像其他类型的值一样被操作、传递和赋值。匿名函数是一种特殊的函数,它没有固定的函数名,可以在代码中被直接定义和使用。匿名函数在Go语言中具有重要的地位,它们常用…...

MobileNet、MobileNetV2和MobileNetV3创新点总结
当谈论MobileNet、MobileNetV2和MobileNetV3时,我们指的是一系列基于深度学习的轻量级神经网络架构,这些架构旨在在保持高度准确性的同时减少模型的计算和参数量。以下是它们各自的创新点的详细总结: MobileNet: 深度可分离卷积&…...
)
算法:数据转换处理2(云台显控)
#define DISPLAYFUNC #include"define.h" extern OS_EVENT *KEYMsg; uchar mBlank[21] = " " ; u c h a r s t r v g a [ ] = " 0.00 V "; uchar str_vga[] = "0.00V...

让大数据平台数据安全可见-行云管家
数字化经济在快速发展,大数据时代已经到来,大数据已经成为企业和政府决策的重要依据。然而大数据行业快速发展所带来的一系列安全问题也继续解决,例如数据安全更难保障,例如认证体系不完善等等。为此行云管家推出了大数据平台数据…...
- 页面设计与布局)
微信小程序开发教学系列(3)- 页面设计与布局
3. 页面设计与布局 在微信小程序开发中,页面的设计和布局是非常重要的。一个好的页面设计可以提升用户体验,并使小程序更加吸引人。本章节将介绍如何设计和布局微信小程序的页面。 3.1 页面结构和样式的创建和设置 在创建微信小程序页面时,…...
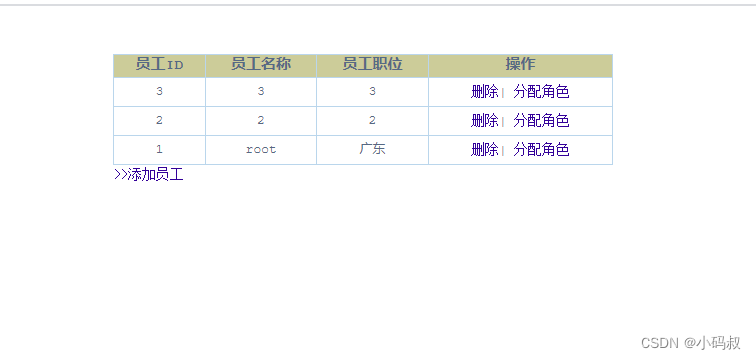
基于JSP+Servlet+mysql员工权限管理系统
基于JSPServletmysql员工权限管理系统 一、系统介绍二、功能展示四、其他系统实现五、获取源码 一、系统介绍 项目类型:Java web项目 项目名称:基于JSPServlet的员工权限管理系统[qxxt] 项目架构:B/S架构 开发语言:Java语言 …...
Qt 自定义提示框 右下角冒泡
网页右下角上经常会出现一些提示性的信息,B/S有的东西,C/S当然也可以有,就像QQ的消息提示一样! 实现一个类似的东西并不困难,只要想明白原理实现起来就很简单了! 实现原理: (1&#…...

js、PHP连接外卖小票机打印机方案(调用佳博、芯烨等)
前言: 目前开发需要用到电脑直接连接外卖小票机打印小票,查阅各种资料,使用 6612345浏览器 终于解决了这个问题。 效果: PHP、js直接连接小票机并且自动出票。 支持的小票机: 目前测试可以的有:电脑A4打印…...

window定时备份MySQL数据库,默认备份7天,一小时备份一次
echo off setlocalrem 在Windows中添加任务计划以执行批处理脚本,请按照以下步骤操作:rem 打开Windows的“任务计划程序”应用程序。你可以通过按下Win R键,在运行对话框中输入taskschd.msc,然后按回车键来打开它。rem 在任务计划…...
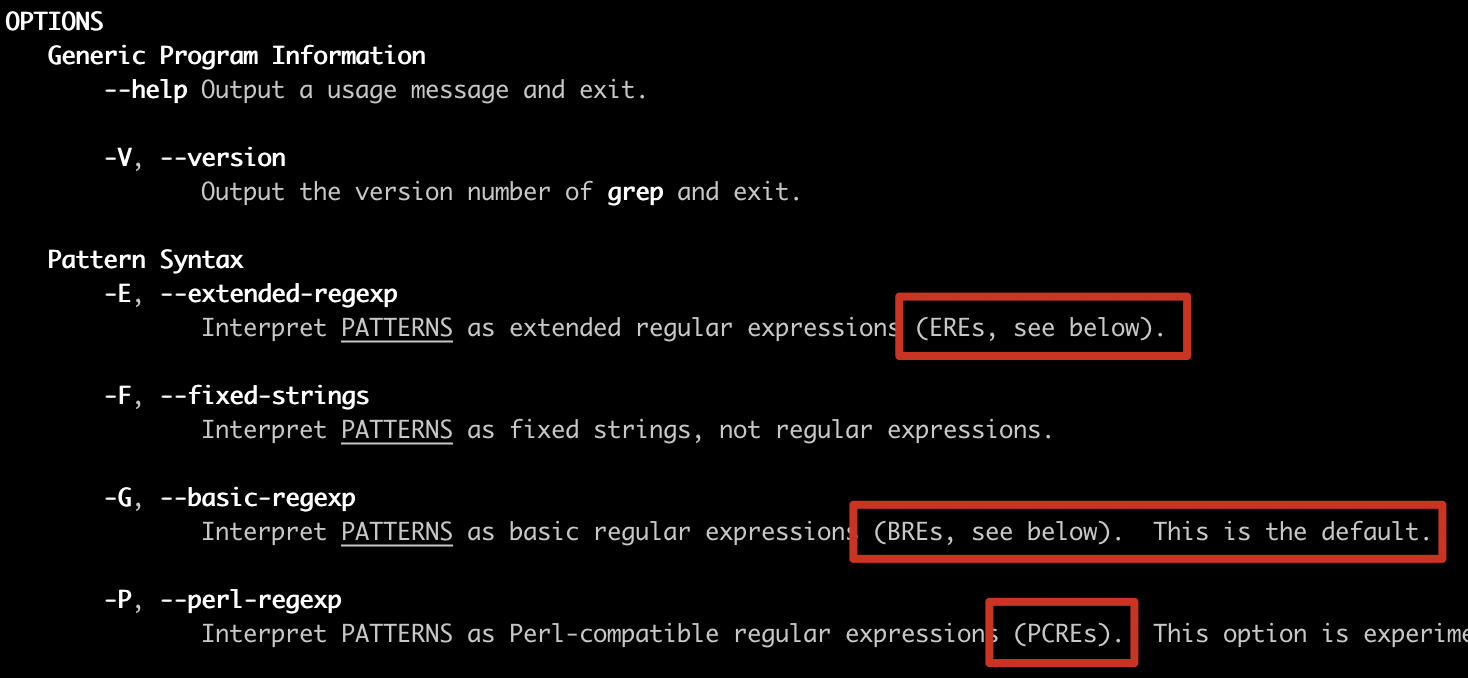
正则中常见的流派及其特性
目前正则表达式主要有两大流派(Flavor):POSIX 流派与 PCRE 流派。 1、 POSIX 流派 POSIX 规范定义了正则表达式的两种标准: BRE 标准(Basic Regular Expression 基本正则表达式);ERE 标准&am…...

.net6.0引用的dll放置单独的文件夹
.net6.0 采用原有的设置方法不起作用 <?xml version"1.0" encoding"utf-8" ?> <configuration><startup> <supportedRuntime version"v4.0" sku".NETFramework,Versionv4.8" /></startup><runtim…...

CMake:检测外部库---自定义find模块
CMake:检测外部库---自定义find模块 导言项目结构CMakeLists.txt附录 导言 上一篇,我们了解了CMake其中一种自定义检测外部库的方式,本篇将展示通过编写一个find模块来定位系统上的ZeroMQ库,以便能够在非Unix操作系统上检测该库。 项目结构…...

vue直接使用高德api
第一步:在index.html 引入 <script src"https://webapi.amap.com/maps?v2.0&key你的key"></script>第二步:在你需要地图的时候 放入 <template><div style"width: 200px; height: 200px"><div id&q…...

Setting
目录 1 Setting 1.1.1 getChildList 1.1.2 getGroupList 1.1.3 setListener setOnChildClickListenermSettingList.setOnChildClickListener(new OnChildClickListener() {onChildClick...

时序预测 | Matlab实现SO-CNN-BiGRU蛇群算法优化卷积双向门控循环单元时间序列预测
时序预测 | Matlab实现SO-CNN-BiGRU蛇群算法优化卷积双向门控循环单元时间序列预测 目录 时序预测 | Matlab实现SO-CNN-BiGRU蛇群算法优化卷积双向门控循环单元时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 时序预测 | Matlab实现SO-CNN-BiGRU蛇群算法优化…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
