To_Heart—题解——P6234 [eJOI2019] T形覆盖
link.
突然很想写这篇题解。虽然题目不算难。
考场只有30分是为什么呢?看来是我没有完全理解这道题目吧!
首先很明显的转换是,把 T 型覆盖看成十字形,再考虑最后减去某一块的贡献。
然后然后直接往原图上面放十字形!对于每一个十字的中心来说,实际上它只需要三个相邻的方块就可以了。而我们发现两个十字重合的部分不会超过两个方块,也就是说把这两个方块任意分配给两个人,就能保证这两个每个人都只会舍弃一个方块。
因为每次两个十字的重合最多只能让每个点丢弃一个方块,并且每次重合至少有一个十字会丢弃掉一个方块,所以惊天的结论是我们可以直接计算整个十字连通块的中心点和非中心点的个数。如果非中心点的个数大于等于中心点的个数的三倍,那么当前连通块一定合法,否则不能保证每个十字的中心点都能分配到刚好三个非中心点,即无解。
但是可能有非中心点的个数大于中心点的个数的三倍。这种情况说明所有的十字都只重合了一个点,那么必须要丢掉一个非中心点。因为要权值最大所以丢掉最小权值的就好了。
其实这个的实现方式有很多,但是我使用了并查集。为什么呢?因为其他题解就是用的并查集啊!
然后并查集需要注意的点就是不能选择中心点啊。中心点的权值设为最大值好不好。
#include<bits/stdc++.h>
using namespace std;int n,m,k;
int a[1000005];
int ID(int x,int y){return (x-1)*m+y;
}
int pre[1000005],dp[1000005];
int sz[1000005][2];
long long sum[1000005];bool vis[1000005];struct zz{int x,y;
}t[1000005];int Find(int x){if(pre[x]!=x) pre[x]=Find(pre[x]);return pre[x];
}
void Join(int x,int y){int fx=Find(x),fy=Find(y);if(fx==fy) return ;pre[fy]=fx,sum[fx]+=sum[fy],dp[fx]=min(dp[fx],dp[fy]),sz[fx][0]+=sz[fy][0],sz[fx][1]+=sz[fy][1];
}int fx[5]={0,1,-1,0,0};
int fy[5]={0,0,0,1,-1};int main(){
// freopen("t-covering.in","r",stdin);
// freopen("t-covering.out","w",stdout);cin>>n>>m;for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) scanf("%d",&a[ID(i,j)]);cin>>k;for(int i=1,x,y;i<=k;i++) scanf("%d%d",&x,&y),t[i]=(zz){x+1,y+1};for(int i=1;i<=k;i++) vis[ID(t[i].x,t[i].y)]=1;for(int i=1;i<=n*m;i++){pre[i]=i,sum[i]=a[i],dp[i]=a[i],sz[i][vis[i]]=1;if(vis[i]) dp[i]=0x3f3f3f3f; }for(int i=1;i<=k;i++) for(int j=1;j<=4;j++){int x=t[i].x,y=t[i].y;int dx=x+fx[j],dy=y+fy[j];if(dx<=0||dx>n||dy<=0||dy>m) continue;Join(ID(x,y),ID(dx,dy)); }long long ans=0;memset(vis,0,sizeof vis);for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){int x=(ID(i,j));int fx=Find(x);if(vis[fx]) continue; vis[fx]=1;if(sz[fx][0]<sz[fx][1]*3) return printf("No\n"),0;else if(sz[fx][0]==sz[fx][1]*3) ans+=sum[fx];else ans+=sum[fx]-dp[fx];}cout<<ans<<endl;return 0;
}
相关文章:

To_Heart—题解——P6234 [eJOI2019] T形覆盖
link. 突然很想写这篇题解。虽然题目不算难。 考场只有30分是为什么呢?看来是我没有完全理解这道题目吧! 首先很明显的转换是,把 T 型覆盖看成十字形,再考虑最后减去某一块的贡献。 然后然后直接往原图上面放十字形!对于每一个…...

[软件工具]精灵标注助手目标检测数据集格式转VOC或者yolo
有时候我们拿到一个数据集发现是xml文件格式如下: <?xml version"1.0" ?> <doc><path>C:\Users\Administrator\Desktop\test\000000000074.jpg</path><outputs><object><item><name>dog</name>…...
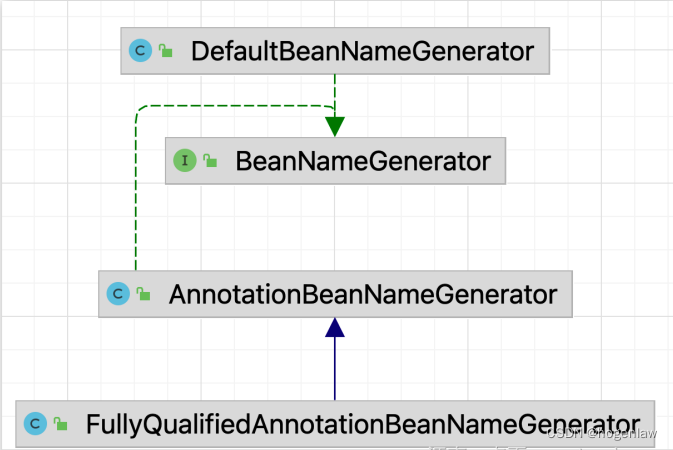
Spring BeanName自动生成原理
先看代码演示 项目先定义一个User类 public class User {private String name;Overridepublic String toString() {return "User{" "name" name \ };}public String getName() {return name;}public void setName(String name) {this.name name;} }…...
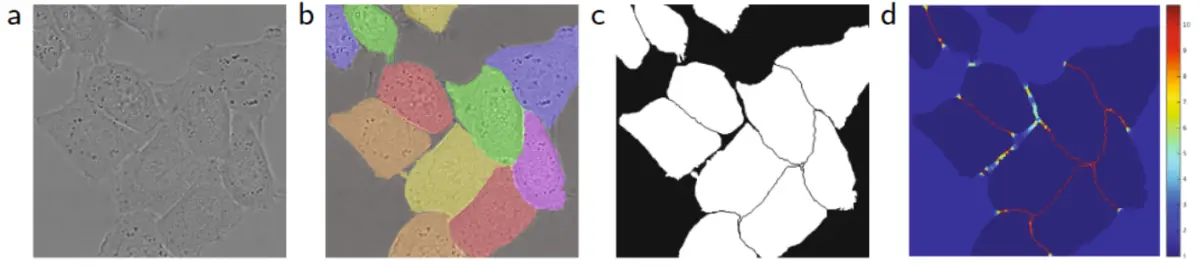
论文阅读_图形图像_U-NET
name_en: U-Net: Convolutional Networks for Biomedical Image Segmentation name_ch: U-Net:用于生物医学图像分割的卷积网络 addr: http://link.springer.com/10.1007/978-3-319-24574-4_28 doi: 10.1007/978-3-319-24574-4_28 date_read: 2023-02-08 date_publi…...

基于热交换算法优化的BP神经网络(预测应用) - 附代码
基于热交换算法优化的BP神经网络(预测应用) - 附代码 文章目录 基于热交换算法优化的BP神经网络(预测应用) - 附代码1.数据介绍2.热交换优化BP神经网络2.1 BP神经网络参数设置2.2 热交换算法应用 4.测试结果:5.Matlab代…...

基于秃鹰算法优化的BP神经网络(预测应用) - 附代码
基于秃鹰算法优化的BP神经网络(预测应用) - 附代码 文章目录 基于秃鹰算法优化的BP神经网络(预测应用) - 附代码1.数据介绍2.秃鹰优化BP神经网络2.1 BP神经网络参数设置2.2 秃鹰算法应用 4.测试结果:5.Matlab代码 摘要…...
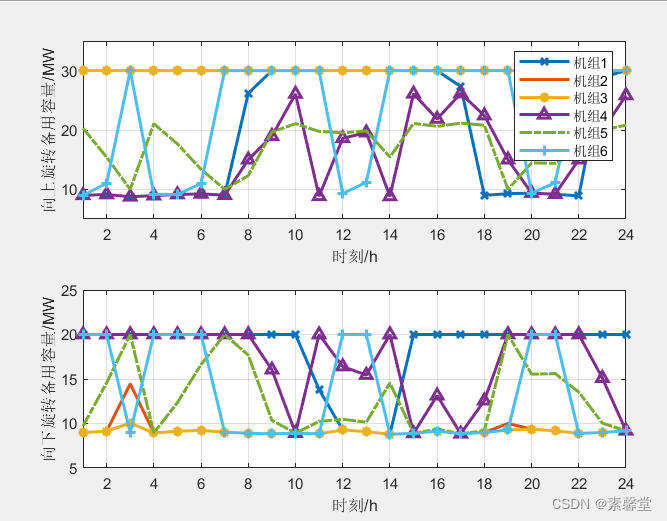
2.文章复现《热电联产系统在区域综合能源系统中的定容选址研究》(附matlab程序)
0.代码链接 1.简述 光热发电是大规模利用太阳能的新兴方式,其储热系 统能够调节光热电站的出力特性,进而缓解光热电站并网带来的火电机组调峰问题。合理配置光热电站储热容量,能够 有效降低火电机组调峰成本。该文提出一种光热电站储热容 量配…...
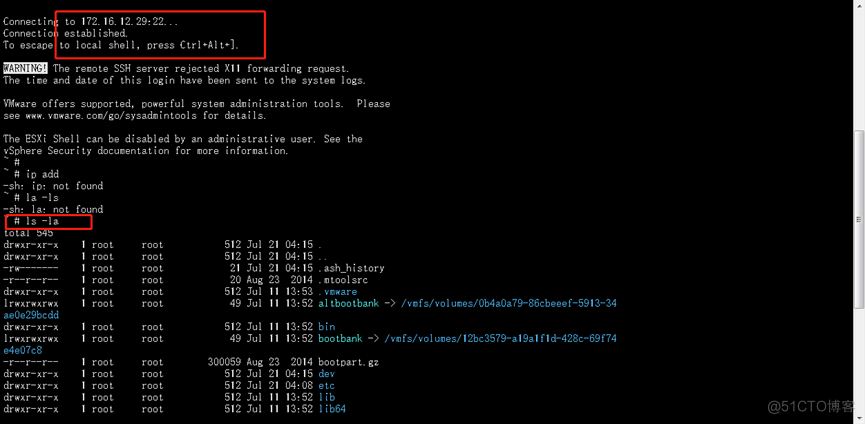
如何开启esxi主机的ssh远程连接
环境:esxi主机,说明:esxi主机默认ssh是不开启的,需要人工手动启动,也可以设置同esxi主机一起开机启动。 1、找到esxi主机,点击“配置”那里,再点击右边的属性,如图所示: …...

Android Studio实现解析HTML获取json,解析json图片URL,将URL存到list,进行瀑布流展示
目录 效果build.gradle(app)添加的依赖(用不上的可以不加)AndroidManifest.xml错误activity_main.xmlitem_image.xmlMainActivityImage适配器ImageModel 接收图片URL 效果 build.gradle(app)添加的依赖&…...

Centos7 交叉编译QT5.9.9源码 AArch64架构
环境准备 centos7 镜像 下载地址:http://mirrors.aliyun.com/centos/7.9.2009/isos/x86_64/ aarch64交叉编译链 下载地址:https://releases.linaro.org/components/toolchain/binaries/7.3-2018.05/aarch64-linux-gnu/ QT5.9.9源代码 下载地址࿱…...
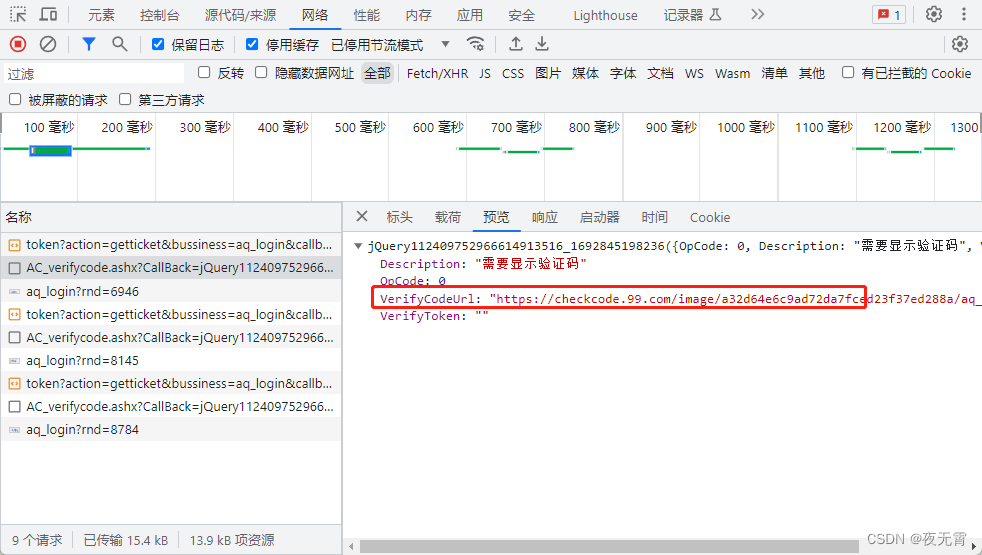
爬虫逆向实战(二十)--某99网站登录
一、数据接口分析 主页地址:某99网站 1、抓包 通过抓包可以发现登录接口是AC_userlogin 2、判断是否有加密参数 请求参数是否加密? 通过查看“载荷”可以发现txtPassword和aws是加密参数 请求头是否加密? 无响应是否加密? 无…...

【C# 基础精讲】LINQ to Objects查询
LINQ to Objects是LINQ技术在C#中的一种应用,它专门用于对内存中的对象集合进行查询和操作。通过使用LINQ to Objects,您可以使用统一的语法来查询、过滤、排序、分组等操作各种.NET对象。本文将详细介绍LINQ to Objects的基本概念、常见的操作和示例&am…...

【力扣】209. 长度最小的子数组 <滑动窗口>
【力扣】209. 长度最小的子数组 给定一个含有 n 个正整数的数组和一个正整数 target 。 找出该数组中满足其和 ≥ target 的长度最小的连续子数组 [numsl, numsl1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。 示例 1&a…...

帮助中心应该用什么工具做?
在线帮助中心是指一个位于互联网上的资源平台,提供给用户获取产品或服务相关信息、解决问题以及获取技术支持的渠道。它通常包含了组织化的知识库、常见问题解答(FAQ)、操作指南、教程视频、用户手册等内容。在线帮助中心的主要目标是为用户提…...

前端面试:【跨域与安全】跨域问题及解决方案
嗨,亲爱的Web开发者!在构建现代Web应用时,跨域问题和安全性一直是不可忽视的挑战之一。本文将深入探讨跨域问题的背景以及解决方案,以确保你的应用既安全又能与其他域名的资源进行互操作。 1. 什么是跨域问题? 跨域问…...
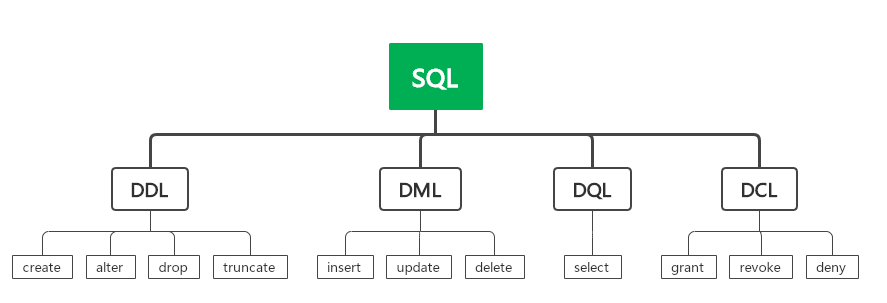
【SQL中DDL DML DQL DCL所包含的命令】
SQL中DDL DML DQL DCL所包含的命令 关于DDL、DML、DQL、DCL的定义和适用范围如下: 数据定义语言(Data Definition Language,DDL): DDL用于创建、修改和删除数据库中的表、视图、索引等对象。它的主要命令包括CREATE、A…...
LeetCode150道面试经典题-- 二叉树的最大深度(简单)
1.题目 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。 2.示例 3.思路 深度优先遍历 一个二叉树要查询到最大深度,可以将问题转为从根节点出发,查看左右子树的最大深度&am…...
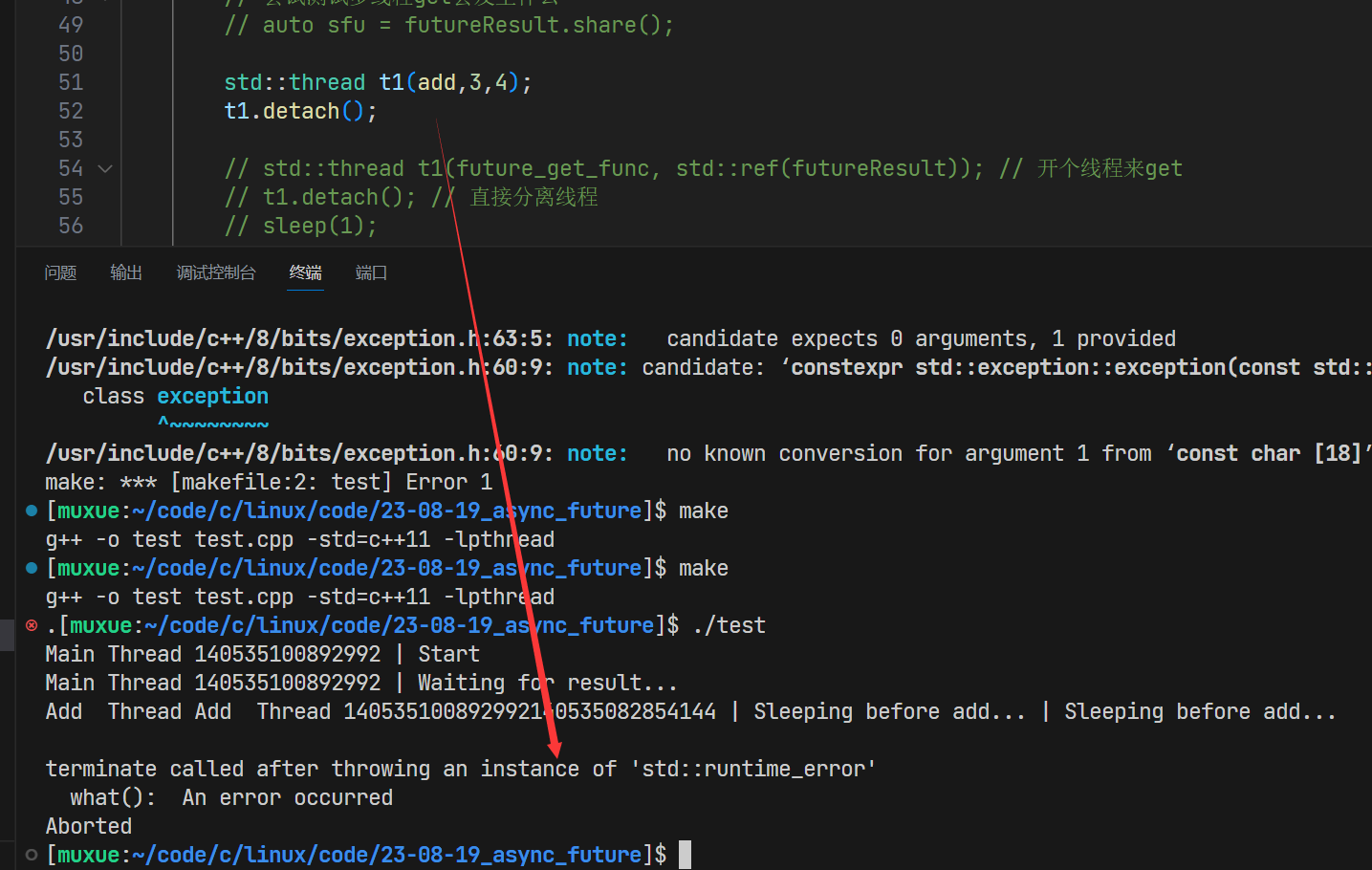
【C++11】future和async等
C11的future和async等关键字 1.async和future的概念 std::async 和 std::future 是 C11 引入的标准库功能,用于实现异步编程,使得在多线程环境中更容易处理并行任务。它们可以帮助你在不同线程中执行函数,并且能够方便地获取函数的结果。 在…...
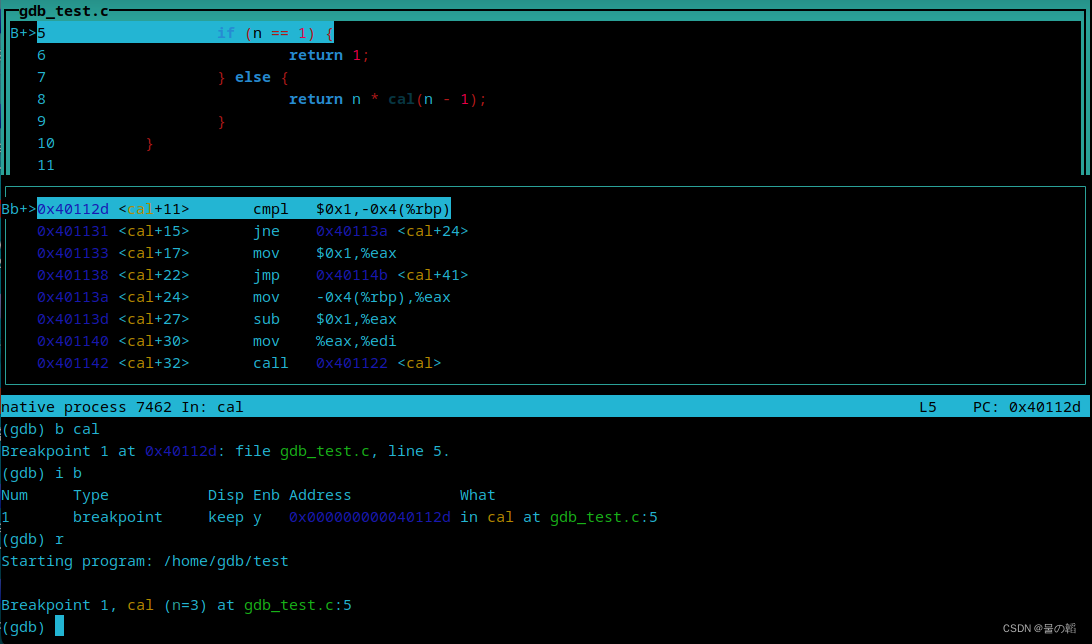
Linux 系统下 GDB 调试器的使用
文章目录 简介GDB 的介绍GDB 的使用 GDB 常用命令及示例查看相关操作断点相关操作运行相关操作变量相关操作分隔窗口操作 简介 GDB 的介绍 GDB 是 GNU 调试程序,是用来调试 C 和 C 程序的调试器。它可以让程序开发者在程序运行时观察程序的内部结构和内存的使用情况…...

个人首次使用UniAPP使用注意事项以及踩坑
个人首次使用UniAPP 使用注意事项以及踩坑 自我记录 持续更新 1.vscode 插件 uni-create-view 快速nui-app页面的 uni-helper uni-app代码提示的 uniapp小程序扩展 鼠标悬停查文档 Error Lens 行内提示报错 "types": ["dcloudio/types", "mini…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
