【C++之容器篇】AVL树的底层原理和使用
目录
- 前言
- 一、AVL树
- 二、AVL树的底层实现
- 1. 结点类型的定义
- 2. AVL树的定义
- 3. 查找函数
- 4. 插入函数(重难点)
- 三、判断平衡树的方法
前言
AVL树其实是在搜索树的基础上加上一些限制因素,从而使搜索树的结构保持相对平衡,通过前面我们对二叉搜索树的学习,我们知道,如果我们向一棵二叉搜索树中插入一些有序的数据,那么整棵树就会偏向于一边,从而使整棵树失去平衡,那么在查找的时候就会效率低下,退化为顺序表的效率了,今天我们学习的AVL树本质上就是为了解决二叉搜索树中失去平衡的问题,为了控制二叉搜索树中的子树的左右子树的高度差保持相对平衡,我们采取在树中的每一个结点中增加一个变量来记录每一个结点的平衡因子,我们可以定义平衡因子为该子树的右子树的高度-左子树的高度。
一、AVL树
AVL树是一棵二叉搜索树,并且除了具备二叉搜索树的性质,还具备以下的性质:
- 树的左右子树的高度差不超过1,可以通过平衡因子进行控制
- 树中的每一棵子树都是AVL树
二、AVL树的底层实现
1. 结点类型的定义
// AVL树的结点
template <class K,class V>
struct AVLTreeNode
{// 构造函数AVLTreeNode(const pair<K,V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}// 成员变量pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;// 平衡因子:左右子树的高度差(右子树高度-左子树高度)int _bf;
};AVL树中的结点需要包含三个指针,即指向左子树的指针,指向右子树的指针,指向父亲结点的指针,还需要一个存储数据的pair结构,还需要有一个平衡因子,其中的构造函数是对一个新生成的结点中的数据进行初始化,新生成的结点中就是通过给定的kv来初始化_kv,然后左子树和右子树和父亲结点均为空,需要确定后再由外面手动更新,其中的平衡因子是由该结点的左右子树的情况来决定的,显然一个新的结点中不存在左右子树,所以平衡因子显然为0。
2. AVL树的定义
template <class K,class V>
class AVLTree
{// 使用结点typedef AVLTreeNode<K, V> Node;
public:// 成员函数private:// 成员变量Node* _root = nullptr;
};
和前面学习的树型结构的实现一样,刚开始默认为空树,所以_root给了一个缺省值,在AVL树的类中需要使用到树的结点,所以为了方便表示,可以将树的结点进行重定义。
3. 查找函数
查找函数的实现比较简单,和二叉搜索树中的查找函数的实现几乎一致,只是需要知道,这里的数据是pair类型,pair类型中有first和second,其中first是key,second是value,外面需要通过key去进行查找,也就是需要通过kv.first去进行比较。
// 查找函数bool Find(const pair<K, V>& kv){Node* cur = _root;while (cur){if (kv.first < cur->_kv.first){// 左子树找cur = cur->_left;}else if(kv.first>cur->_kv.first){// 右子树找cur = cur->_right;}else{// 找到了return true;}}return false;}
4. 插入函数(重难点)
AVL树的插入函数的底层其实首先是按照搜索树的规则进行插入,然后再通过平衡因子的调整使整棵树的高度保持相对平衡。
- 插入的过程
- 按照搜索树的规则进行插入
- 更新平衡因子,最坏的情况需要沿着路径一直更新到根:如果孩子是插入在左边,则父亲的平衡因子–,如果孩子是插入在父亲的右边,则平衡因子++,当父亲的平衡因子更新之后,需要根据父亲更新后的平衡因子确定作何调整,此时需要进行分类讨论
- 更新后父亲的平衡因子为0:说明更新前父亲的平衡因子是1或者-1,当更新前父亲的平衡因子是1使,说明这棵子树的右子树比较高,孩子插入在左子树上,所以父亲的高度没有发生变化,不需要继续更新,当更新前父亲的平衡因子是-1时,说明父亲的左子树比较高,此时孩子插入在父亲的右子树上,父亲的高度保持不变,所以不需要更新。
- 更新后父亲的平衡因子是1或者-1:说明更新前父亲的平衡因子是0,如果更新后父亲的平衡因子变成1,说明孩子插入在父亲的右子树上,导致此时父亲的右子树变高,所以需要继续往上更新。如果更新后父亲的平衡因子变成-1,说明孩子插入在父亲的左子树上,导致父亲的左子树变高,所以需要继续往上更新,往上迭代的方式:先更新cur结点,再通过cur结点算其父亲。
- 更新后父亲的平衡因子是2或者-2,此时树的平衡因子不符合AVL树的规则,需要进行调整(旋转),下面重点介绍四种旋转方式。
- 左旋:适用于旋转的子树是整体是右边比较高,首先需要先保存一些关键的结点指针,分别是通过parent计算得出的爷爷结点(pparent),右子树(subR),右子树的左孩子(subRL),旋转的过程中需要注意两个细节:parent可能是整棵树中的某一棵子树,也可能是整棵树的根节点,subRL不一定存在。在将parent->_right指向subRL之后,需要更新subRL->_parent,但是subRL不一定存在,所以此时需要先判断一下。如果parent是根节点,则旋转之后需要更新根节点为subR,并且将subR->_parent指向nullptr。如果parent不是根,则此时pparent结点就会发挥作用,需要先判断parent是pparent的左孩子还是右孩子,以确定是让pparent->_left还是pparent->_right托管subR,然后再更新sub->_parent指向pparent。最后还需要更新平衡因子,左旋的过程中动的只是parent和subR的孩子,所以只需要更新这两个结点,并且左旋的结果是使得它们均平衡,所以最终的平衡因子都是0。
- 右旋:右旋和左旋是非常类似的,首先需要先保存一些关键的结点指针:通过parent计算得出的
pparent(parent的父亲),subL(parent的左孩子),subLR(subL的右孩子)。旋转的过程中同样需要注意两个细节:parent可能是整棵树的根节点,也可能只是某一棵子树的根节点,subLR可能存在也可能不存在。如果subLR不存在,则不需要更新subRL->_parent。判断parent:如果parent是整棵树的根节点,则需要更新根节点为subL,然后将根节点的父亲指向空指针,如果parent不是根节点,则此时pparent就会起作用,此时判断parent是pparent->_left还是pparent->_right,以决定让pparent->_left还是pparent->_right托管subL,然后再更新subL->_parent指向pparent。最后更新平衡因子,和左旋过程类似,该过程中只是动了parent和subL的孩子,所以只需要更新这两个结点,并且最终都是平衡,所以最终的平衡因子都是0。- 左右双旋:这个双旋适合于parent的右子树高,cur的左子树高的情况,先保存一些关键的结点:
subR(parent->_right),subRL(subR->_left)旋转的过程,首先让cur右旋,使整棵子树保持右边高,然后再让parent进行左旋。双旋之后,subRL会到根的位置,parent到根的左子树,subR到根的右子树(可以通过画图进行分析),最后调整平衡因子,调整平衡因子需要根据旋转前的subRL的平衡因子(保存为bf)的情况进行分类讨论。如果bf == 0,则subRL是新插入的结点,此时parent,subR,subRL的平衡因子都更新成0。 如果bf == -1,则新节点插入在subRL的左子树,旋转过程中这个新节点会分给左边(parent),所以左边的平衡因子会被平衡故最终的平衡因子为:parent->_bf = 0,subR->_bf = 1,subRL->_bf = 0。如果bf == 1,则新结点插入在subR的右子树,旋转过程中,这个新节点会分给右边(subR),所以最终右边的平衡因子会被平衡,故最终的平衡因子为:parent->_bf = -1,subR->_bf = 0,subRL->_bf = 0。- 右左双旋:这个双旋适合于parent的左子树高,cur的右子树高的情况,先保存一些关键的结点:subL(parent->_left),subLR(parent->_left->_right),旋转过程:先对subL进行左旋,转化为整体的左子树比较高,再对整体进行右旋,使整棵树保持相对平衡。旋转的结果:subLR到根的位置,parent到根的右子树,subL到根的左子树,再通过旋转前subLR的平衡因子(保存为bf)进行分类讨论:如果
bf == 0,则说明subLR是新插入的结点,最终的平衡因子:parent->_bf = 0,subL->_bf = 0,subLR->_bf = 0,如果bf == -1,则说明新结点插入在subLR的左边,这个新结点在旋转的过程中会分给左边(subL),所以左边的平衡因子会被平衡,故最终的平衡因子为:parent->_bf = 1,subL->_bf = 0,subLR->_bf = 0,如果bf == 1,说明新插入的结点插入在subLR的右边,这个新节点在旋转的过程中会分给右边(parent),右边的平衡因子会被平衡,所以最终的平衡因子为:parent->_bf = 0,subL->_bf = -1,subLR->_bf = 0
下面给出上述讲解过程中需要用到的操作的代码:
- 左旋
// 左旋void RotateL(Node* parent){// 保存一些关键的结点指针Node* pparent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;if (parent == _root){// parent是根_root = subR;_root->_parent = nullptr;}else{// parent不是根if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}// 更新平衡因子parent->_bf = 0;subR->_bf = 0;}
- 右旋
// 右旋void RotateR(Node* parent){// 保存一些关键结点Node* pparent = parent->_parent;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}subL->_right = parent;parent->_parent = subL;// 判断parent是否为根if (parent == _root){// parent为根_root = subL;_root->_parent = nullptr;}else{// parent不是根if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}subL->_parent = pparent;}// 更新平衡因子parent->_bf = 0;subL->_bf = 0;}
- 左右双旋
// 先左旋再右旋void RotateLR(Node* parent){// 先保存一些关键信息Node* subL = parent->_left;Node* subLR = subL->_right;// 旋转前先保存subLR的平衡因子int bf = subLR->_bf;// 旋转RotateL(subL);RotateR(parent);// 更新平衡因子if (bf == 0){// subLR就算新插入的结点parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else if (bf == -1){// 新插入的结点插入在subLR的左边parent->_bf = 1;subLR->_bf = 0;subL->_bf = 0;}else if (bf == 1){// 新插入的结点插入在subLR的右边parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else{// 其他错误assert(false);}}
- 右左双旋
// 先右旋再左旋void RotateRL(Node* parent){// 保存一些关键信息Node* subR = parent->_right;Node* subRL = subR->_left;// 保存subRL的平衡因子int bf = subRL->_bf;// 旋转RotateR(subR);RotateL(parent);// 更新平衡因子if (bf == 0){// subRL是新插入的结点parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else if (bf == -1){// 新插入的结点插入在subRL的左边parent->_bf = 0;subR->_bf = 1;subRL->_bf = 0;}else if (bf == 1){// 新插入的结点插入在subRL的右边parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else{// 其他错误assert(false);}}
三、判断平衡树的方法
思路:采用递归的方法,先判断当前树是否为平衡树(本节采用平衡因子进行判断),如果当前为平衡树,则继续递归判断左子树和右子树是否为平衡树
- 代码:
// 求树的高度的子函数size_t _TreeHeight(Node* root){if (root == nullptr){// 空树return 0;}// 非空树// 先算左子树的高度size_t LeftHeight = _TreeHeight(root->_left);// 再算右子树的高度size_t RightHeight = _TreeHeight(root->_right);return LeftHeight > RightHeight ? LeftHeight + 1 : RightHeight + 1;}// 判断平衡树的子函数bool _IsBalanceTree(Node* root){if (root == nullptr){// 空树return true;}// 先算左子树高度size_t LeftHeight = _TreeHeight(root->_left);// 再算右子树高度size_t RightHeight = _TreeHeight(root->_right);// 计算平衡因子int bf = RightHeight - LeftHeight;if (abs(bf) > 1){cout << "树失衡,不断平衡树" << endl;return false;}if (bf != root->_bf){cout << "平衡因子于实际不符合,不是平衡树" << endl;return false;}// 递归判断左右子树return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}// 判断平衡树bool IsBalanceTree(){return _IsBalanceTree(_root);}
相关文章:

【C++之容器篇】AVL树的底层原理和使用
目录前言一、AVL树二、AVL树的底层实现1. 结点类型的定义2. AVL树的定义3. 查找函数4. 插入函数(重难点)三、判断平衡树的方法前言 AVL树其实是在搜索树的基础上加上一些限制因素,从而使搜索树的结构保持相对平衡,通过前面我们对二叉搜索树的学习&#x…...

从交换机安全配置看常见局域网攻击
前言 构建零信任网络,自然离不开网络准入(NAC),这就涉及到交换机的一些安全测试,于是有了此文《从交换机安全配置看常见局域网攻击》。 交换机安全配置 如本文标题所说从交换机安全配置看常见的局域网攻击,那么下面提到的各种攻…...
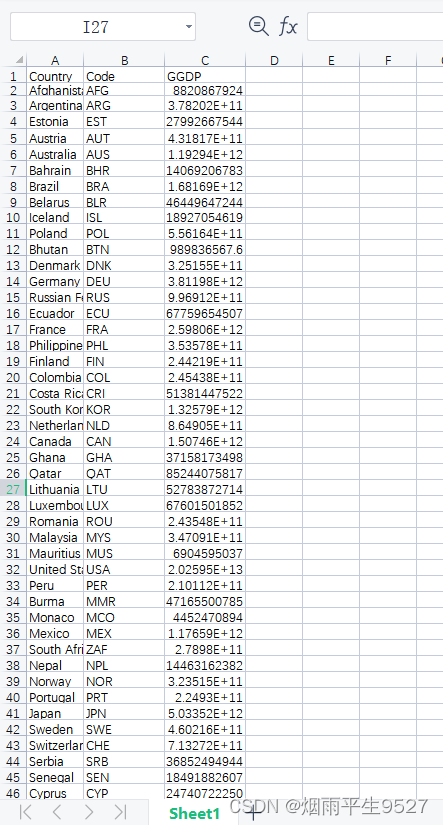
工具篇3.5世界热力图
一、定义 世界热力图是一种地图形式,它使用颜色的变化来显示世界各个地区的某种指标(如 GDP、人口、气候等)的分布和密度。通常,世界热力图会使用不同的颜色来表示数据的变化,例如使用蓝色表示低值,红色表…...

2023-02-20 leetcode-insertionSortList
摘要: 记录leetcode-insertionSortList的反思 要求: https://leetcode.cn/problems/insertion-sort-list/ Given the head of a singly linked list, sort the list using insertion sort, and return the sorted lists head. The steps of the insertion sort algorithm: In…...

LeetCode初级算法题:环形链表+排列硬币+合并两个有序数组java解法
环形链表排列硬币合并两个有序数组(没错,出现过一次的LeetCode合并数组又双叒叕出现了!)经典算法题java解法 目录1 环形链表题目描述解题思路与代码解法一:哈希表解法二:双指针2 排列硬币题目描述解题思路与…...

网络编程学习一
1、初识网络编程2、网络编程三要素3、三要素(IP)4、IPV4的一些小细节5、Inetaddress类的使用package com.leitao.demo.network;import java.net.InetAddress; import java.net.UnknownHostException;/*** Description: TODO* Author LeiTao* Date 2023/2…...

Javascript 立即执行函数
IIFE,一般称为立即执行函数。你可能会问我,*“嘿!我知道正常的函数表达式是什么样子的,但是 IIFE 到底是什么?”。*好吧,这正是我今天要在本文中回答的问题。 函数表达式 在了解立即调用函数表达式之前,让…...
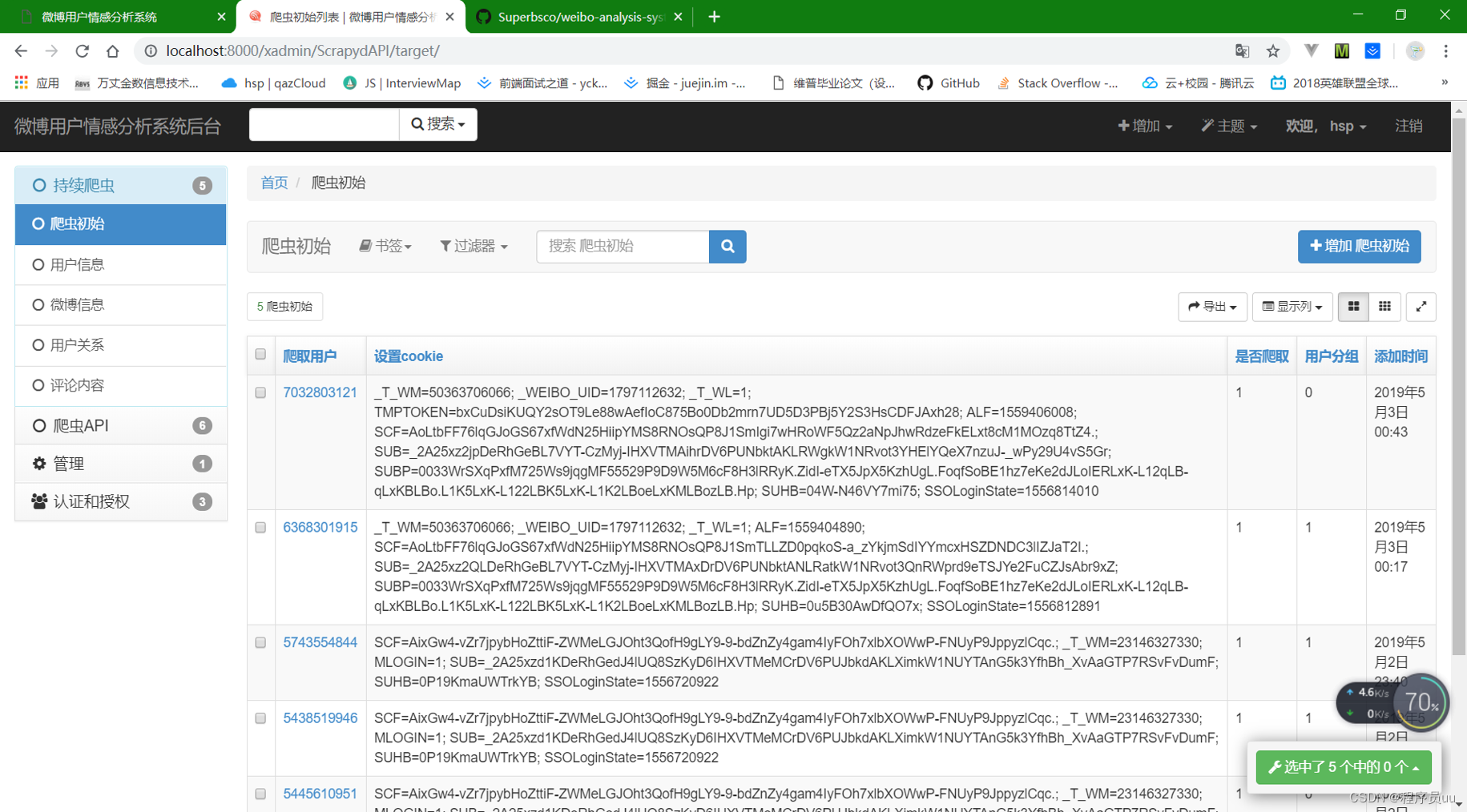
基于Django和vue的微博用户情感分析系统
完整代码:https://download.csdn.net/download/weixin_55771290/87471350概述这里简单说明一下项目下下来直接跑起的方法。前提先搞好python环境和vue环境,保证你有一个账户密码连上数据库mysql。1、pip install requirements.txt 安装python包2、修改mysql数据库的…...

【C++】IO流
🌈欢迎来到C专栏~~IO流 (꒪ꇴ꒪(꒪ꇴ꒪ )🐣,我是Scort目前状态:大三非科班啃C中🌍博客主页:张小姐的猫~江湖背景快上车🚘,握好方向盘跟我有一起打天下嘞!送给自己的一句鸡汤…...
【论文速递】ACL 2021-CLEVE: 事件抽取的对比预训练
【论文速递】ACL 2021-CLEVE: 事件抽取的对比预训练 【论文原文】:CLEVE: Contrastive Pre-training for Event Extraction 【作者信息】:Wang, Ziqi and Wang, Xiaozhi and Han, Xu and Lin, Yankai and Hou, Lei and Liu, Zhiyuan and Li, Peng and …...
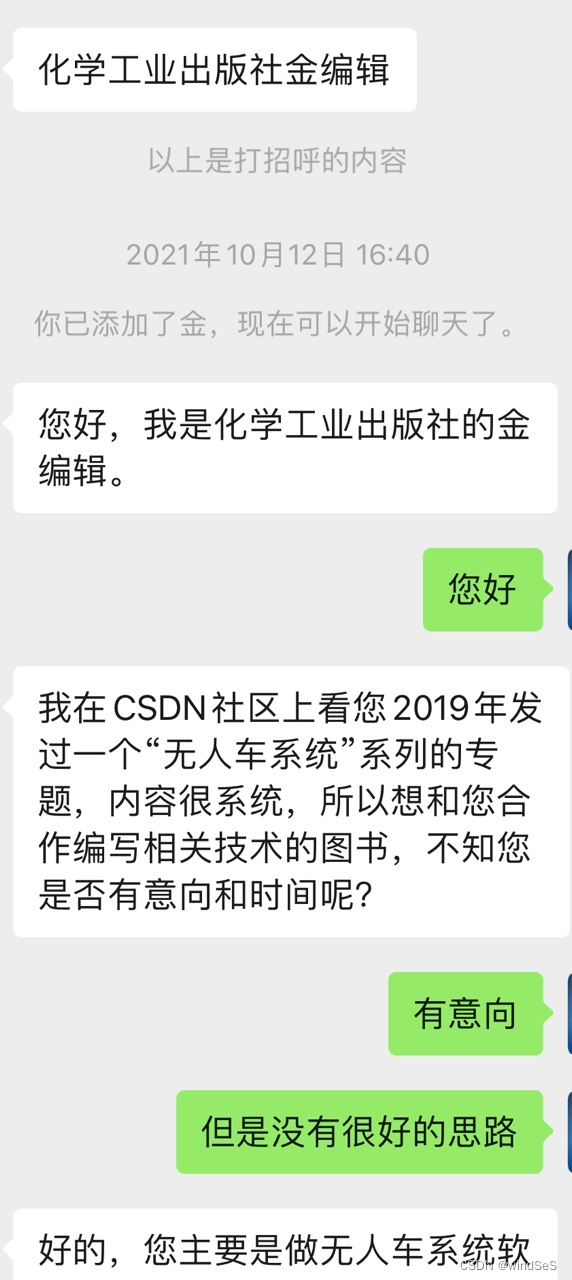
《自动驾驶规划入门》专栏结语
一、 源起 2021年10月12日,化学工业出版社的金编辑根据博客中留下的微信号联系上我,问我有没有出书的想法。从小到大,书与文字在我心里是有着神圣地位的。我在“想试试”与“害怕做不好”这两种矛盾的心情中,还是先应了下来。签了…...
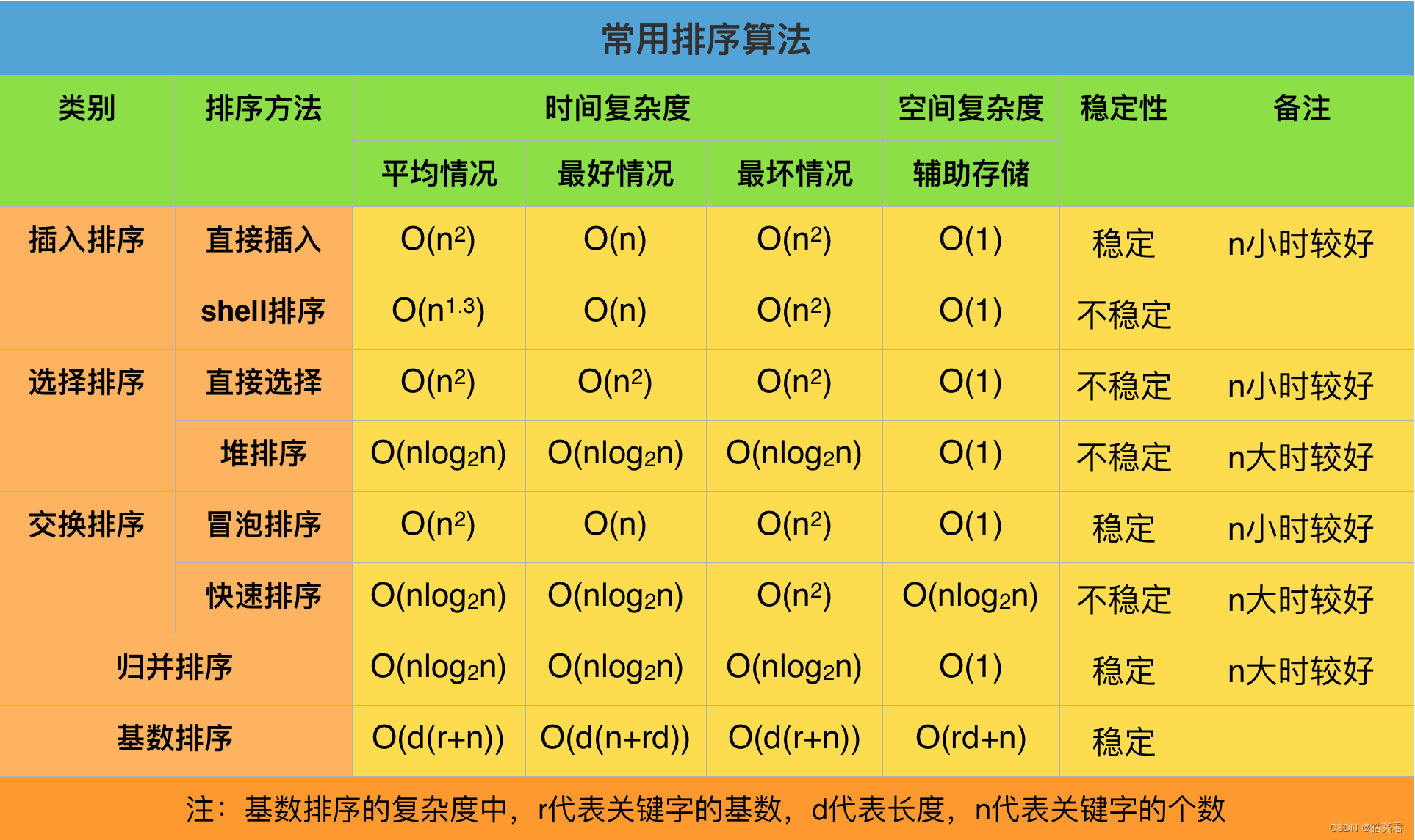
【数据结构与算法】2.八大经典排序
文章目录简介1.分析排序算法2.插入排序2.1.直接插入排序2.2.希尔排序3.选择排序3.1.直接选择排序3.2.堆排序3.2.1.堆的数据结构3.2.2.算法实现4.交换排序4.1.冒泡排序4.2.快速排序5.归并排序6.基数排序7.八大排序算法总结简介 排序对于任何一个程序员来说,可能都不会…...
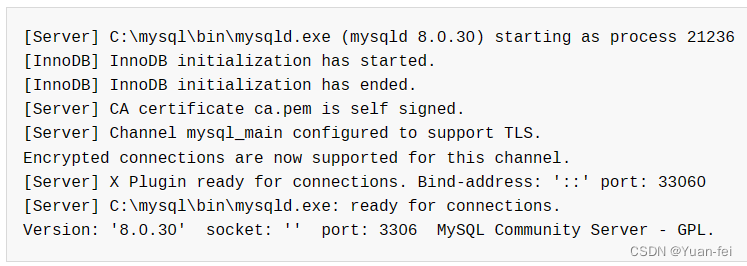
Windows 免安装版mysql,快速配置教程
简单步骤 下载并解压mysql压缩包,把 “<mysql根目录>/bin” 路径添加到系统环境变量path中命令行执行 mysqld --initialize --console,初始化data目录(数据库表文件默认存放在" <mysql安装根目录>/data "目录下&#…...

空间误差分析:统一的应用导向处理(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
【C++】引用、内联函数、auto关键字、范围for、nullptr
引用什么叫引用引用的特性常引用使用场景传值、传引用效率比较引用和指针的区别内联函数auto关键字(C11)基于范围的for循环(C11)指针空值nullptr(C11)引用 什么叫引用 引用不是新定义一个变量,而是给已存在变量取了一个别名,编译器不会为引用变量开辟内…...

pytest数据驱动
文章目录一、数据驱动概念二、数据驱动yaml1、yaml的基本语法:2、yaml支持的数据格式:3、安装4、使用5、读取方法a、目录结构b、yaml文件c、测试方法d、测试用例e、测试结果三、数据驱动excel1、安装导入2、操作3、读取方法a、目录结构b、excel文件c、测…...
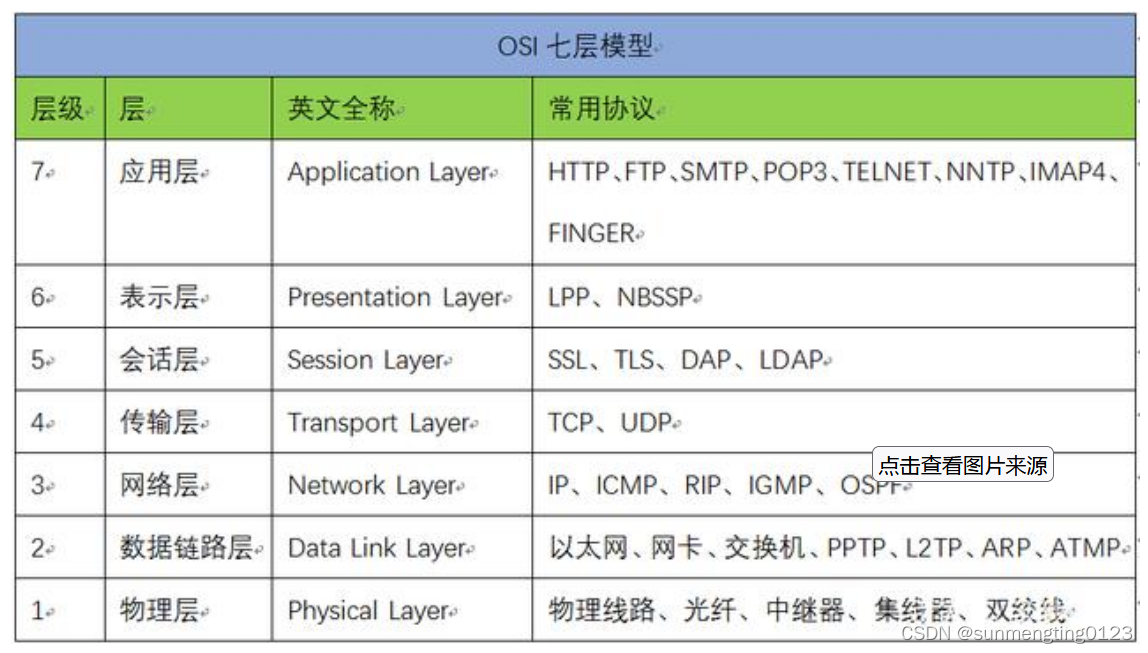
OSI七层网络模型
应用层 定义了各种应用协议规范数据格式:HTTP协议、HTTPS协议、FTP协议、DNS协议、TFTP、SMTP等等。 表示层 翻译工作。提供一种公共语言、通信。 会话层 1、可以从校验点继续恢复数据进行重传。——大文件 2、自动收发,自动寻址的功能。 传输层 1、…...

易基因|MeRIP-seq揭示m6A RNA甲基化通过调控组蛋白泛素化来促进癌症生长和进展:Cancer Res
大家好,这里是专注表观组学十余年,领跑多组学科研服务的易基因。2022年05月16日,《Cancer Res》杂志发表了题为“M6A RNA Methylation Regulates Histone Ubiquitination to Support Cancer Growth and Progression”的研究论文,该…...

Java 日期处理踩过的坑
前言 整理Java日期处理遇到过的问题,希望对大家有帮助 制作不易,一键三连,谢谢大家。 1.用 Calendar 设置时间的坑 反例: //提供者模式获取实例Calendar calendar Calendar.getInstance();//获取当前时间Date currentDate c…...

一文吃透 Spring 中的IOC和DI(二)
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
