【位运算】算法实战
文章目录
- 一、算法原理
- 常见的位运算总结
- 二、算法实战
- 1. leetcode面试题01.01. 判断字符是否唯一
- 2. leetcode268 丢失的数字
- 3. leetcode371 两整数之和
- 4. leetcode004 只出现一次的数字II
- 5. leetcode面试题17.19. 消失的两个数字
- 三、总结
一、算法原理
计算机中的数据都以二进制形式存储和处理,位运算直接对二进制位进行操作。常见的位运算符包括与(&)、或(|)、异或(^)、取反(~)和左移(<<)、右移(>>)等。

常见的位运算总结
基础位运算

给一个数n,确定它的二进制表示中第x位是0还是1
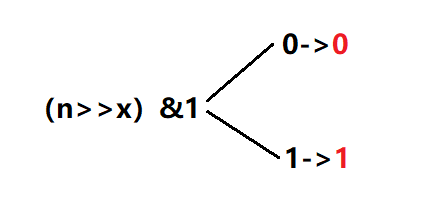
将一个数n的二进制表示的第x位修改成1
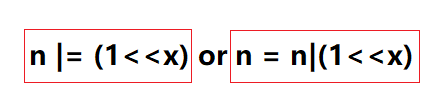
将一个数n的二进制表示的第x位修改成0
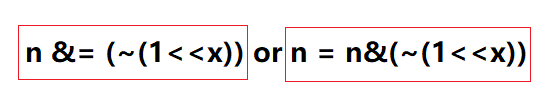
位图的思想
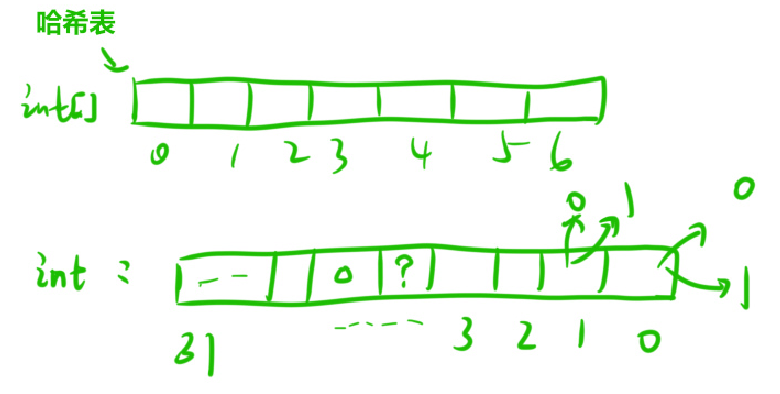
提取一个数(n)二进制表示中最右侧的1
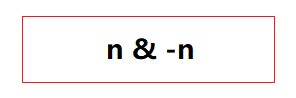
干掉一个数(n)二进制表示中最右侧的1
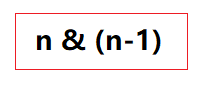
位运算的优先级:能加括号就加括号异或(^)运算的运算律

二、算法实战
1. leetcode面试题01.01. 判断字符是否唯一
判断字符是否唯一
解题思路:位图的思想
这道题目我们可以使用位图的思想来解决,因为题目告诉我们字符串中只有小写字母,所以我们只需要一个int类型的整数来充当位图的32个bit位即可。
首先,将位图的所有bit位置为零,默认字符串中的字符都未在位图中出现过。然后遍历整个字符串,检测该字符是否在位图中出现过,如果当前字符未在位图中出现过,说明当前字符是第一次出现,此时我们将其在位图中的位置(当前字符-'a')置为1即可,然后接着向后遍历字符串,如果该字符再次出现,我们就可以从位图中检测到该字符已经在出现过了。直接返回false即可,否则继续向后遍历字符串,如果遍历所有字符后发现都只出现一次,则说明该字符串符合题意。
代码实现:
class Solution {
public:bool isUnique(string astr) {int num = 0;for(int i = 0; i < astr.size(); i++){int index = astr[i] - 'a';if(((num>>index) & 1) == 1)return false;elsenum |= 1 << index;}return true;}
};
2. leetcode268 丢失的数字
丢失的数字
解题思路:异或运算
因为题目中告诉我们数组中【1~n】丢失了一个数字,所以我们可以先将数组中的数字 ^ 起来,然后在将这个 ^ 的结果与【1~n】中所有的数字异或,因为按位 ^ 运算满足交换律和结合律,所以按位 ^ 的结果中,丢失的数字出现了一次,其余的数字都出现了两次,将这一堆数字异或起来,结果即为丢失的数字。
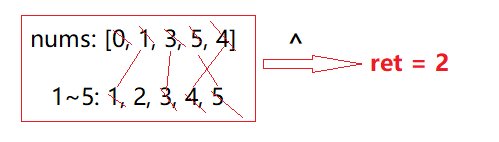
代码实现:
class Solution {
public:int missingNumber(vector<int>& nums) {int ret = 0;for(auto e : nums)ret ^= e;for(int i = 1; i <= nums.size(); i++)ret ^= i;return ret;}
};
3. leetcode371 两整数之和
两整数之和
解题思路:异或运算-无进位相加
因为题目要求我们不能使用运算符+和-来计算两整数之和,因此我们可以将整数 a 和 b 的和,拆分为 a 和 b 的无进位相加结果与进位结果的和,无进位相加结果 我们可以使用两整数^来实现,进位结果我们可以使用(a & b) << 1来实现。下面我们来举一个例子:

每次将无进位相加结果与进位结果的和分别赋予a和b,循环此过程,直到进位为 0。最终a就是我们所要求的结果。当我们赋给无符号类型一个超出它表示范围的值时,结果是初始值对无符号类型表示数值总数取模的余数。因此,我们可以使用无符号类型来防止溢出。
代码实现:
lass Solution {
public:int getSum(int a, int b) {while(b != 0){int x = a ^ b; // 先算出无进位相加的结果unsigned int carry = (a & b) << 1; // 算出进位a = x;b = carry;}return a;}
};
4. leetcode004 只出现一次的数字II
只出现一次的数字II
解题思路:
数组中的每个元素的每一个二进制位不是1就是0,而题目中又告诉我们只有一个元素出现一次,其余元素都出现了三次,所以对于数组中的每一个元素 x,我们使用位运算 (x >> i) & 1 得到 x 的第 i 个二进制位,并将它们相加再对 3 取余,得到的结果一定为 0 或 1,即为答案的第 i 个二进制位。
所以,答案的第 i 个二进制位就是数组中所有元素的第 i 个二进制位之和除以 3 的余数。可以先初始化一个ret = 0,然后根据余数的值来判断该数对应的二进制位应该置为0还是1,如果余数为1,我们则需要手动将该位置置为1,ret |= (1 << i),否则则不需要处理。
代码实现:
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for(int i = 0; i < 32; i++){int cnt = 0;for(auto e : nums)cnt += ((e>>i)&1);if(cnt % 3)ret |= (1 << i);}return ret;}
};
5. leetcode面试题17.19. 消失的两个数字
消失的两个数字
解题思路:
这道题目其实我们可以用力扣的第260题 只出现一次的数字III 的思想来做,具体解决方式如下:
因为数组中包含从 1 到 N 所有的整数,但其中缺了两个数字,现在数组的长度为n。所以数组中原本应该包含的数字是【1,n + 2】。我们可以将原来数组中的数字和【1,n + 2】,组合到一起,现在我们就可以将问题转化一下:求数组中只出现一次的两个数字。
解决这个问题我们可以分为两步:整体异或和分组异或。整体异或:将题目给出的数组中的所有数字和【1,n + 2】中所包含的数字全部异或起来,得到的结果就是只出现一次的两个数字的异或结果:a^b。接下来我们需要提取出该数字二进制表示中最低位的1。假设该位置为第k位,我们就可以把 所有数中的元素(题目中给出的数字和【1,n + 2】的数字)分成两类,其中一类包含所有二进制表示的第 k 位为 0 的数,另一类包含所有二进制表示的第 k 位为 1 的数。
- 对于任意一个在 所有元素中 出现两次的元素,该元素的两次出现会被包含在同一类中;
- 对于任意一个在所有元素中只出现了一次的元素,即 x1 和 x2, 他们会被包含在不同的类中。
因此,我们将这两类元素分别异或起来,就可以得到不同的两个结果,一个结果是x1,另一个结果是x2,这两个数字则是只出现一次的两个数字,即本题中我们需要寻找的两个消失的数字。
代码实现:
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {int ret = 0;for(int i = 1; i <= nums.size()+2; i++)ret ^= i;for(auto e : nums) ret ^= e;int lowbit = ret & -ret; // 找出最后一个不同的比特位int ret1 = 0, ret2 = 0;for(int i = 1; i <= nums.size()+2; i++){ // 分组异或if(lowbit & i) ret1 ^= i;else ret2 ^= i;}for(auto e : nums){if(lowbit & e) ret1 ^= e;else ret2 ^= e;}return {ret1, ret2};}
};
三、总结
位运算可以直接操控数字的二进制位,节约内存,使程序运行更快,可靠性高。在算法中使用位运算可以大大降低算法的时间复杂度和空间复杂度,恰当的位运算使用也能使程序变得更加简洁和优美。
相关文章:
【位运算】算法实战
文章目录 一、算法原理常见的位运算总结 二、算法实战1. leetcode面试题01.01. 判断字符是否唯一2. leetcode268 丢失的数字3. leetcode371 两整数之和4. leetcode004 只出现一次的数字II5. leetcode面试题17.19. 消失的两个数字 三、总结 一、算法原理 计算机中的数据都以二进…...

C++构建系统
收集C构建系统(2023): 跟我一起写Makefile (PDF重制版)CMake tutorialConan, software package manager for C and C developersvcpkg-repovcpkgGoogle Bazel Build System { Fast, Correct } — Choose twoGN gn_quick_start当前Chromium构建系统 GYP Generate You…...

“深入探索JVM内部机制:理解Java虚拟机的运行原理“
标题:深入探索JVM内部机制:理解Java虚拟机的运行原理 摘要:本篇博客将深入探索Java虚拟机(JVM)的内部机制,帮助读者理解JVM的运行原理。我们将介绍JVM的组成结构,包括类加载器、运行时数据区域…...

java八股文面试[JVM]——双亲委派模型
1.当AppClassLoader去加载一个class时,它首先不会自己去尝试加载这个类,而是把类加载请求委托给父加载器ExtClassLoader去完成。 2.当ExtClassLoader去加载一个class时,它首先也不会去尝试加载这个类,而是把类加载请求委托给父加载…...

NLP与大模型主题全国师资培训班落地,飞桨持续赋能AI人才培养
为了推动大模型及人工智能相关专业人员的培养,8月11日-8月13日,由中国计算机学会主办、机械工业出版社、北京航空航天大学、百度飞桨联合承办 “CCF群星计划之文心高校行- NLP与大模型”主题师资培训班(以下简称培训班)在北京天信…...

Jupyter Notebook 配置根目录
注:本文是在 Windows 10 上配置 Jupyter Notebook 打开的默认根目录,Linux 同。 步骤一:创建 Jupyter Notebook 配置文件 使用以下命令创建 Jupyter Notebook 配置文件(如果尚未创建): jupyter notebook …...

算法 位运算
文章目录 一、&(按位与)运算符二、|(按位或)运算符三、^(异或)运算符四、~(取反)运算符五、<<(左移)运算符六、>>(右移ÿ…...

Linux 虚拟机常用命令
一、文件/文件夹管理 1. ls命令 就是 list 的缩写,通过 ls 命令不仅可以查看 linux 文件夹包含的文件,而且可以查看文件权限(包括目录、文件夹、文件权限)查看目录信息等等。 ls -a 列出目录所有文件,包含以.开始的隐藏文件ls -A 列出除.…...
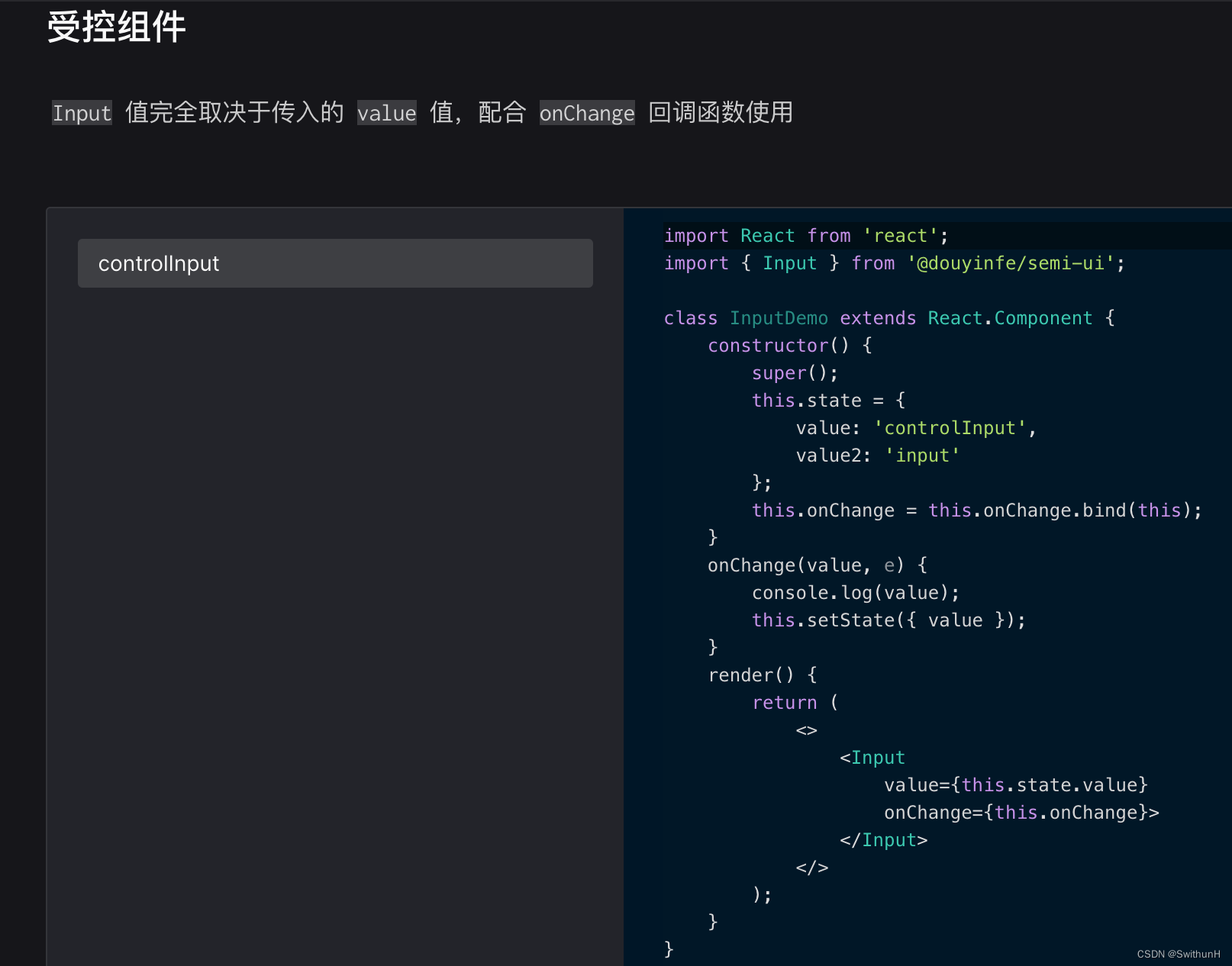
解决抖音semi-ui的Input无法获取到onChange事件
最近在使用semi-ui框架的Input实现一个上传文件功能时遇到了坑,就是无法获取到onChange事件,通过console查看只是拿到了一个文件名。但若是把<Input>换成原生的<input>,就可以正常获取到事件。仔细看了下官方文档,发现…...
免费的png打包plist工具CppTextu,一款把若干资源图片拼接为一张大图的免费工具
经常做游戏打包贴图的都知道,要把图片打包为一张或多张大图,要使用打包工具TexturePacker。 TexturePacker官方版可以直接导入PSD、SWF、PNG、BMP等常见的图片格式,主要用于网页、游戏和动画的制作,它可以将多个小图片汇聚成一个…...
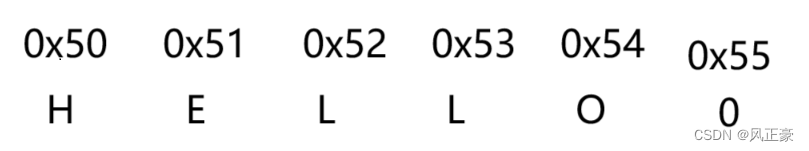
深层次分析字符数组和字符串的区别是什么?
前言 (1)休闲时刻刷B站,看到一个卖课的,发视频问,char arr1[]{‘H’,‘E’,‘L’,‘L’,‘O’};和char arr2[]“HELLO”;区别是什么。 (2)看那个卖课博主一顿分析,最后成功得出&…...
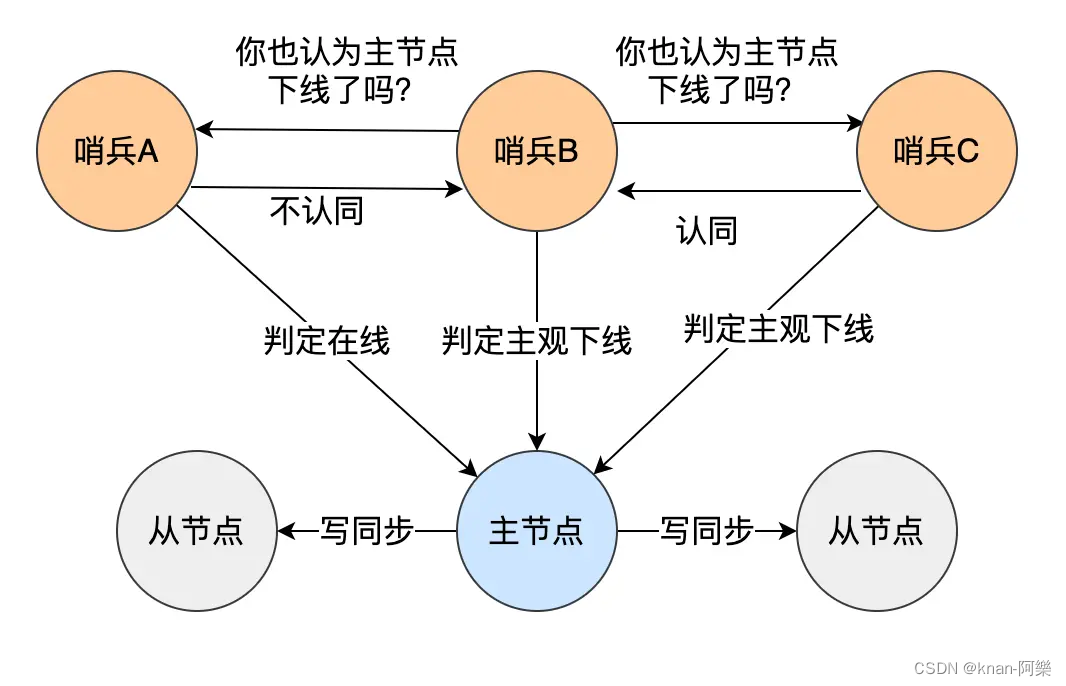
Redis 的主从复制、哨兵模式、集群脑裂
主从复制 主从复制是 Redis 高可用服务最基础的保证,将一台 Redis 主服务器,同步数据到多台 Redis 从服务器上,即一主多从的模式,且主从服务器之间采用的是「读写分离」的方式。 主服务器可以进行读写操作,当发生写操…...

Pycharm通过SSH配置centos上Spark环境
直接在shell进行pyspark进行编程,程序没有办法写得太长,而且我们希望能够实现一个及时给出结果的编程环境,可以使用pycharm连接centos上的spark,进行本地编程,同步到centos系统中运行程序,并把结果返回pych…...

leetcode做题笔记98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 思路一:递归 …...

C# 中Lambda中的的匿名函数
/// <summary>/// 根据设备号,获取故障列表/// </summary>/// <param name"scanCode">主键</param>/// <returns></returns>[HttpGet]public async Task<IActionResult> GetItemPageList(string scanCode){//v…...

铰接式车辆的横向动力学仿真提供车辆模型研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Ubuntu20 安装 libreoffice
1 更新apt-get sudo apt-get update2 安装jdk 查看jdk安装情况 Command java not found, but can be installed with:sudo apt install default-jre # version 2:1.11-72, or sudo apt install openjdk-11-jre-headless # version 11.0.138-0ubuntu1~20.04 sud…...

HTTP协议(JavaEE初阶系列15)
目录 前言: 1.HTTP协议 1.1HTTP协议是什么 1.2HTTP协议的报文格式 1.2.1抓包工具的使用 1.2.2HTTP请求 1.2.3HTTP响应 2.HTTP请求 2.1首行的组成 2.2.1URL的组成 2.2认识“方法”(method) 2.2.1GET方法 2.2.2POST方法 2.2.3GET…...
)
机器学习基础10-审查回归算法(基于波士顿房价的数据集)
上一节介绍了如何审查分类算法,并介绍了六种不同的分类算法,还 用同一个数据集按照相同的方式对它们做了审查,本章将用相同的方式对回归算法进行审查。 在本节将学到: 如何审查机器学习的回归算法。如何审查四种线性分类算法。如…...

基于 CentOS 7 构建 LVS-DR 群集。配置nginx负载均衡。
1、基于 CentOS 7 构建 LVS-DR 群集。 [root132 ~]# nmcli c show NAME UUID TYPE DEVICE ens33 c89f4a1a-d61b-4f24-a260-6232c8be18dc ethernet ens33 [root132 ~]# nmcli c m ens33 ipv4.addresses 192.168.231.200/24 [r…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...