CF 148 D Bag of mice(概率dp求概率)
CF 148 D. Bag of mice(概率dp求概率)
Problem - 148D - Codeforces
大意:袋子里有 w 只白鼠和 b 只黑鼠 ,A和B轮流从袋子里抓,谁先抓到白色谁就赢。A每次随机抓一只,B每次随机抓完一只之后会有另一只随机老鼠跑出来。如果两个人都没有抓到白色则B赢。A先抓,问A赢的概率。
思路:看到数据范围后考虑 概率dp , 设 dp[i][j] 为有 i 个白鼠 j 个黑鼠 A先手获胜的概率
考虑初始化
i == 0 全是黑鼠 , A 必败
dp[i][j] == 0
j == 0 全是白鼠 , A 必胜
dp[i][j] == 1
分情况考虑转移
分四种情况:
1. A 取到白鼠 dp[i][j] += i / (i + j)
2. A 取到黑鼠 , B取到白鼠 dp[i][j] += 0;
3. A 取到黑鼠 , B取到黑鼠 , 白鼠跑出来 dp[i][j] += j / (i + j) * (j - 1) / (i + j - 1) * i / (i + j - 2) * dp[i - 1][j - 2]
4. A 取到黑鼠 , B取到黑鼠 , 黑鼠跑出来 dp[i][j] += j / (i + j) * (j - 1) / (i + j - 1) * (j - 2) / (i + j - 2) * dp[i][j - 3]
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 1e3 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;double dp[N][N];
int x , y;inline double pro(int x , int y){return (double) x / (double) y;
}signed main(){IOScout << fixed << setprecision(10);cin >> x >> y;for(int i = 1 ; i <= x ; i ++) dp[i][0] = 1;for(int i = 1 ; i <= y ; i ++) dp[0][i] = 0;for(int i = 1 ; i <= x ; i ++){for(int j = 1 ; j <= y ; j ++){dp[i][j] += pro(i , i + j);if(i >= 1 && j >= 2) dp[i][j] += pro(j , i + j) * pro(j - 1 , i + j - 1) * pro(i , i + j - 2) * dp[i - 1][j - 2];if(j >= 3) dp[i][j] += pro(j , i + j) * pro(j - 1 , i + j - 1) * pro(j - 2 , i + j - 2) * dp[i][j - 3];}}cout << dp[x][y];return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:
)
CF 148 D Bag of mice(概率dp求概率)
CF 148 D. Bag of mice(概率dp求概率) Problem - 148D - Codeforces 大意:袋子里有 w 只白鼠和 b 只黑鼠 ,A和B轮流从袋子里抓,谁先抓到白色谁就赢。A每次随机抓一只,B每次随机抓完一只之后会有另一只随机老鼠跑出来。如果两个人…...

引入本地 jar 包教程
将本地 jar 包,放到 resource 目录下,在 pom.xml 文件中加入如下依赖: <dependency><groupId>com.hk</groupId><artifactId>examples</artifactId><version>1.0</version><scope>system<…...
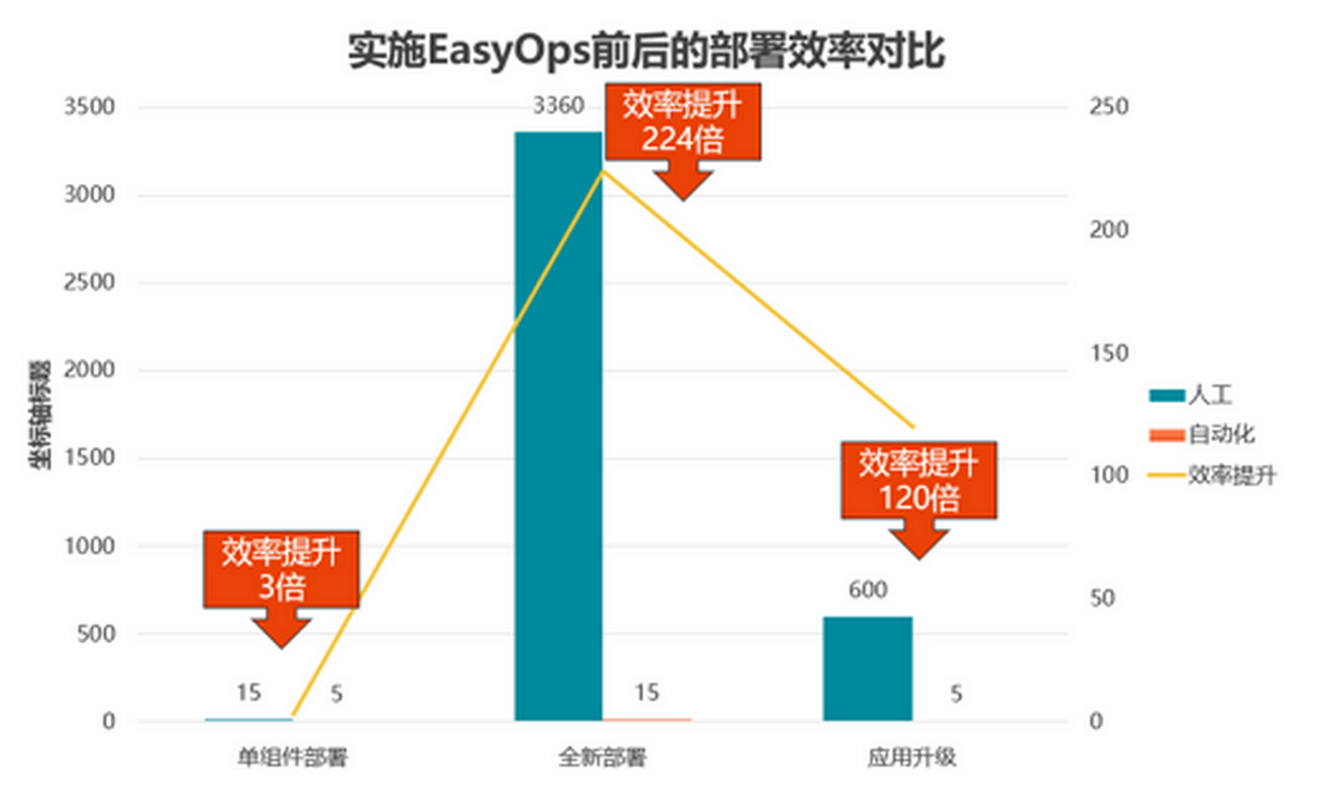
优维产品最佳实践第5期:什么是持续集成?
谈到到DevOps,持续交付流水线是绕不开的一个话题,相对于其他实践,通过流水线来实现快速高质量的交付价值是相对能快速见效的,特别对于开发测试人员,能够获得实实在在的收益。 本期EasyOps产品使用最佳实践,…...
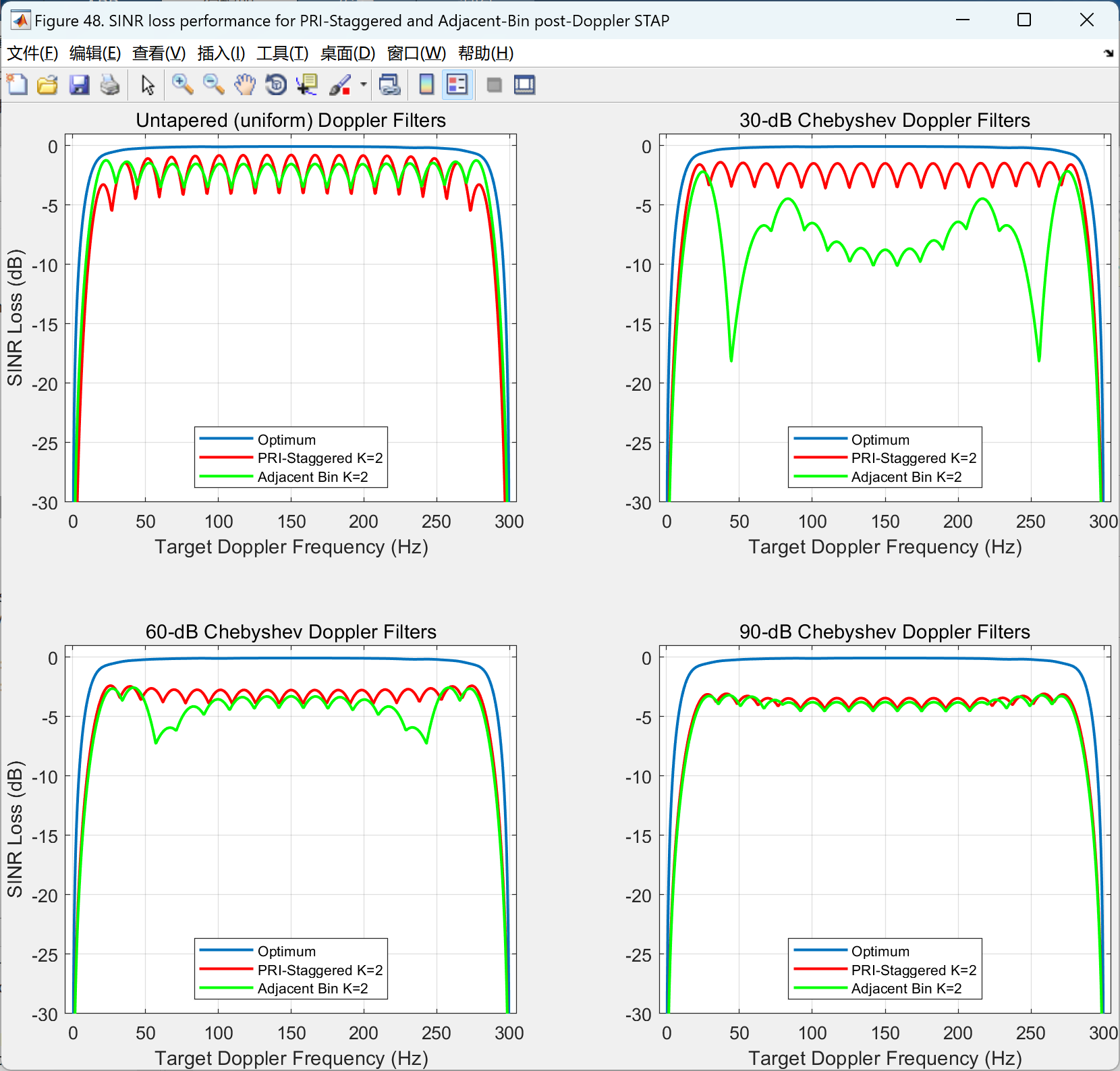
空时自适应处理用于机载雷达——元素空间空时自适应处理(Matla代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

聚观早报 | 青瓷游戏上半年营收3.34亿元;如祺出行冲击IPO
【聚观365】8月26日消息 青瓷游戏上半年营收3.34亿元 如祺出行冲击IPO 索尼互动娱乐将收购Audeze 昆仑万维上半年净利润3.6亿元 T-Mobile计划在未来五周内裁员5000人 青瓷游戏上半年营收3.34亿元 青瓷游戏发布截至2023年6月30日止的中期业绩,财报显示…...

硅谷的魔法:如何塑造了全球技术的未来
硅谷的创新文化简介 硅谷,位于美国加利福尼亚州的圣克拉拉谷,已经从一个半导体产业的中心发展成为全球技术创新的代名词。这里集结了全球最顶尖的技术公司、创业者和投资者,共同创造了一个技术创新的奇迹。 起源与发展 硅谷的起源与斯坦福大…...
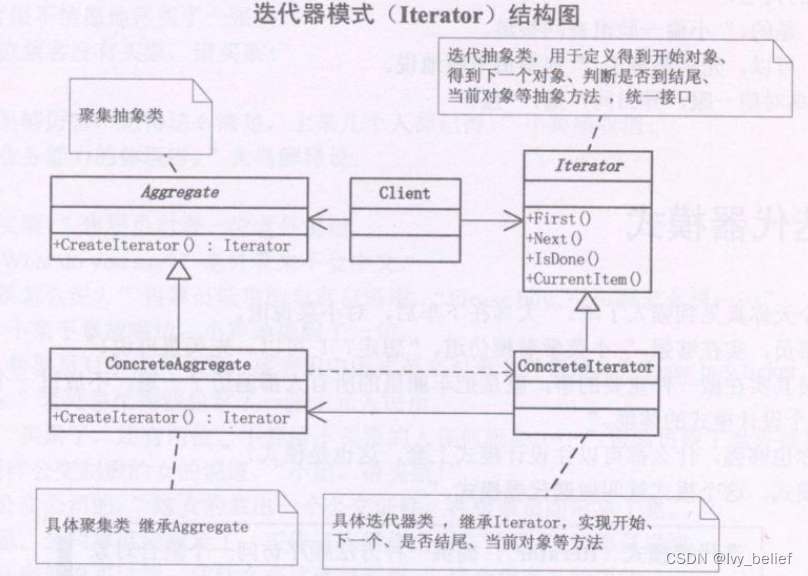
(三)行为模式:4、迭代器模式(Iterator Pattern)(C++示例)
目录 1、迭代器模式(Iterator Pattern)含义 2、迭代器模式的UML图学习 3、迭代器模式的应用场景 4、迭代器模式的优缺点 (1)优点 (2)缺点 5、C实现迭代器模式的实例 1、迭代器模式(Itera…...
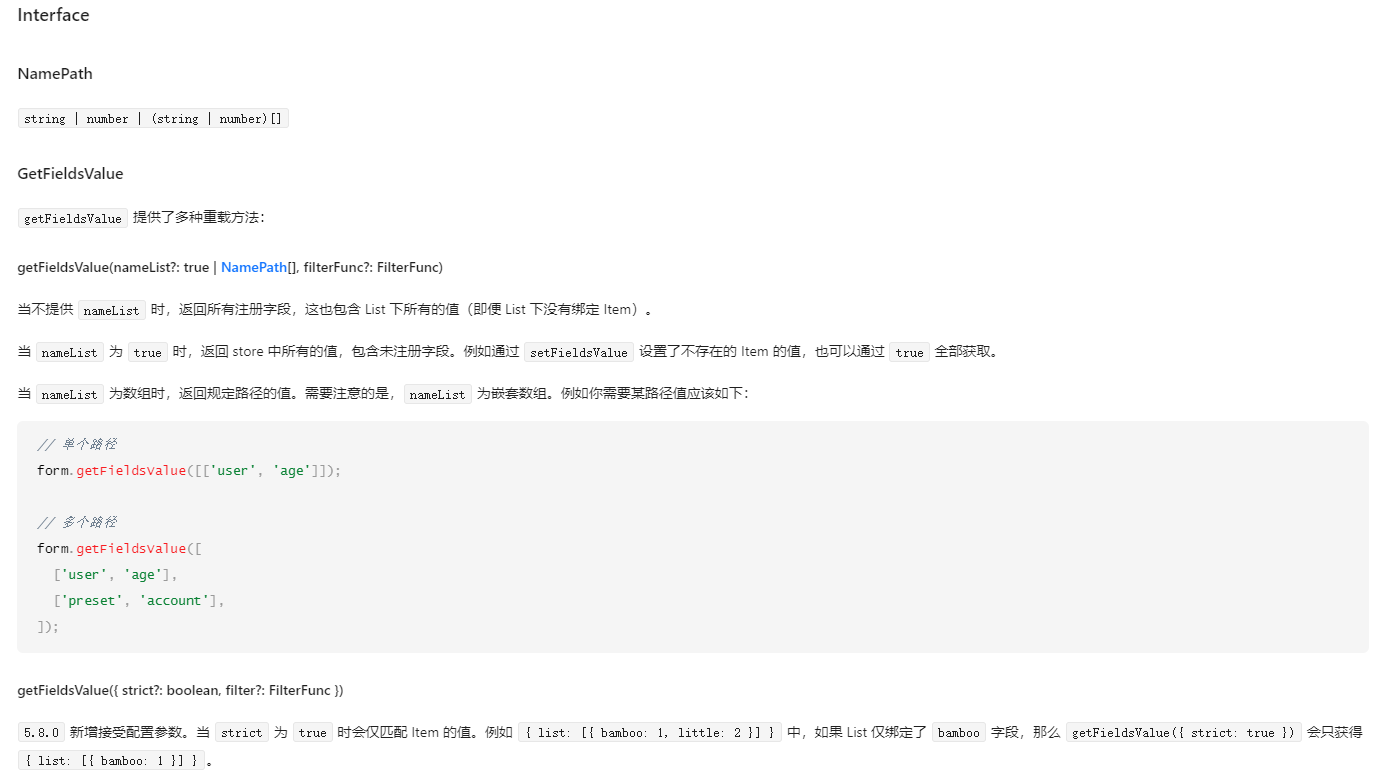
React Antd form.getFieldsValue() 和 form.getFieldsValue(true) 有区别吗?
背景 突然发现 antd 的 getFieldsValue()是可以传一个 true 参数的,如题,React Antd form.getFieldsValue() 和 form.getFieldsValue(true) 有区别吗? 验证 确实不一样 结论 getFieldsValue 提供了多种重载方法: getFieldsValue(name…...

浅谈Java中的观察者模式
观察者模式是软件开发中常用的一种设计模式,它通过定义一对多的依赖关系,使得一个对象(主题)的状态变化可以通知多个其他对象(观察者)。 这种模式的优点是解耦和增加扩展性,用于实现对象之间的…...

C++:命名空间,缺省参数,函数重载,引用,内联函数
个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》 文章目录 前言一、命名空间命名空间的定义命名空间的使用 二、缺省参数缺省参数概念缺省参数分类 三、函数重载函数重载的概念 四、引用引用的概念引用特性引用的使用场景引用与指针的区别 …...
)
2.Vue报错Cannot read properties of undefined (reading ‘then‘)
1.出现报错 Cannot read properties of undefined (reading ‘then’), 代码为 uploadFile(e.target.files[0]).then((res) > {alert(JSON.stringify(res));});2.原因 是因为uploadFile方法没有返回值,于是我又检查了一遍代码,发现我的r…...

【LeetCode 】数组简介
集合列表和数组 本文中介绍的概念为适用于所有编程语言的抽象理论,具体实现会由编程语言的不同而稍有差别。 具体介绍数组之前,我们先来了解一下集合、列表和数组的概念之间的差别。 集合 集合一般被定义为:由一个或多个确定的元素所构成的…...

一文解析block io生命历程
作为存储业务的一个重要组成部分,block IO是非易失存储的唯一路径,它的生命历程每个阶段都直接关乎我们手机的性能、功耗、甚至寿命。本文试图通过block IO的产生、调度、下发、返回的4个阶段,阐述一个block IO的生命历程。 一、什么是块设备…...

Python爬虫学习之旅:从入门到精通,要学多久?
导语: 随着信息时代的发展,大量的数据和信息储存在互联网上,这为我们提供了获取和利用这些数据的机会。而Python爬虫作为一种强大的工具,可以帮助我们从网页中提取数据,并进行进一步的分析和挖掘。然而,对…...
HarmonyOS/OpenHarmony(Stage模型)卡片开发应用上下文Context使用场景一
1.获取应用文件路径 基类Context提供了获取应用文件路径的能力,ApplicationContext、AbilityStageContext、UIAbilityContext和ExtensionContext均继承该能力。应用文件路径属于应用沙箱路径。上述各类Context获取的应用文件路径有所不同。 通过ApplicationContext…...
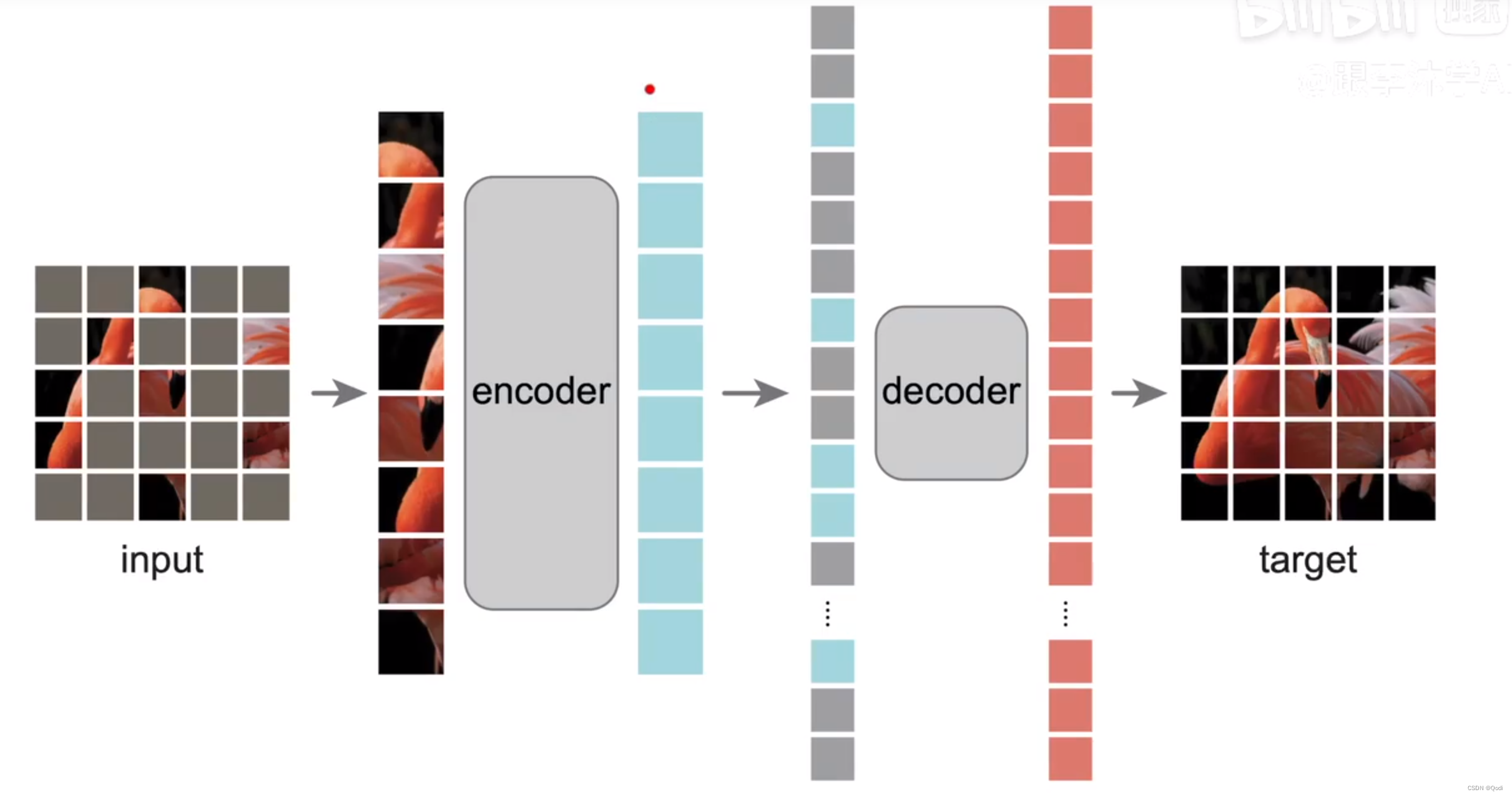
MAE 论文精读 | 在CV领域自监督的Bert思想
1. 背景 之前我们了解了VIT和transformer MAE 是基于VIT的,不过像BERT探索了自监督学习在NLP领域的transformer架构的应用,MAE探索了自监督学习在CV的transformer的应用 论文标题中的Auto就是说标号来自于图片本身,暗示了这种无监督的学习 …...

C++中内存的分配
一个由C/C编译的程序占用的内存分为以下几个部分 1、栈区(stack)— 由编译器自动分配释放 ,存放函数的参数值,局部变量的值等。 2、堆区(heap) — 一般由程序员分配释放, 若程序…...

Qt中的垂直布局QVBoxLayout和水平布局QHBoxLayout
文章目录 QVBoxLayoutQHBoxLayout QVBoxLayout Qt中的垂直布局(Vertical Layout)是用来将控件按垂直方向进行排列的布局管理器。下面是一些常用的Qt Vertical Layout的函数及其用法示例: QVBoxLayout类的构造函数: QVBoxLayout…...

【C#学习笔记】委托和事件
文章目录 委托委托的定义委托实例化委托的调用多播委托 为什么使用委托?官方委托泛型方法和泛型委托 事件为什么要有事件?事件和委托的区别: 题外话——委托与观察者模式 委托 在 .NET 中委托提供后期绑定机制。 后期绑定意味着调用方在你所…...

堆排序简介
概念: 堆排序是一种基于二叉堆数据结构的排序算法。它的概念是通过将待排序的元素构建成一个二叉堆,然后通过不断地取出堆顶元素并重新调整堆的结构来实现排序。 算法步骤: 构建最大堆(或最小堆):将待排…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
