5分钟理解NPL算法 之 马尔可夫链 Markov Chain
马尔可夫链(Markov Chain)
马尔可夫链是一种简单的推理模型。用于描述受当前事件影响下的下一事件发生概率。在预测学科中广泛应用。例如股票预测、文字推理、路线推荐等。
他的核心思路是:假设事件顺序为: X 1 , X 2 , X 3 , . . . . . X_1, X_2, X_3, ..... X1,X2,X3,.....
那么马尔可夫链认为, X 2 的值只与 X 1 的值有关,同样, X 3 的值也只与 X 2 的值有关 X_2的值只与X_1的值有关,同样,X_3的值也只与X_2的值有关 X2的值只与X1的值有关,同样,X3的值也只与X2的值有关
举个栗子
假设你正在策划旅游路线,当然是希望旅游地点之间是相近的且有序的,所以你的第一站目的地会理所应当的会直接影响第二站的选择。以北京和深圳为例:
以矩阵方式描述就显得更直观些:
下一站概率 = P = [ 北京 深圳 北京 0.2 0.3 深圳 0.7 0.5 ] 下一站概率= P=\left[ \begin{matrix} & 北京 & 深圳 \\ 北京 & 0.2 & 0.3 \\ 深圳 & 0.7 & 0.5 \\ \end{matrix} \right] 下一站概率=P= 北京深圳北京0.20.7深圳0.30.5
如上所示,如果你现在身在北京,下一站为深圳的概率是0.3,继续停留在北京的概率是0.2,
如果当前身在深圳,下一站去北京的概率是0.7,继续停留在深圳的概率是0.5
那如果我想知道,已经在两地辗转移动两次后的下一站概率怎么办呢?
只需要将前后的关系矩阵相乘:
移动 2 次后的下一站概率 = P = [ 北京 深圳 北京 0.2 0.3 深圳 0.7 0.5 ] [ 北京 深圳 北京 0.2 0.3 深圳 0.7 0.5 ] 移动2次后的下一站概率 = P= \left[ \begin{matrix} & 北京 & 深圳 \\ 北京 & 0.2 & 0.3 \\ 深圳 & 0.7 & 0.5 \\ \end{matrix} \right] \left[ \begin{matrix} & 北京 & 深圳 \\ 北京 & 0.2& 0.3 \\ 深圳 & 0.7 & 0.5 \\ \end{matrix} \right] 移动2次后的下一站概率=P= 北京深圳北京0.20.7深圳0.30.5 北京深圳北京0.20.7深圳0.30.5
= [ 北京 深圳 北京 0.2 ∗ 0.2 + 0.3 ∗ 0.7 0.2 ∗ 0.3 + 0.3 ∗ 0.5 深圳 0.7 ∗ 0.2 + 0.5 ∗ 0.7 0.7 ∗ 0.3 + 0.5 ∗ 0.5 ] =\left[ \begin{matrix} & 北京 & 深圳 \\ 北京 & 0.2 * 0.2 + 0.3 *0.7 & 0.2* 0.3+0.3*0.5 \\ 深圳 & 0.7 * 0.2 + 0.5*0.7 & 0.7*0.3 + 0.5*0.5 \\ \end{matrix} \right] = 北京深圳北京0.2∗0.2+0.3∗0.70.7∗0.2+0.5∗0.7深圳0.2∗0.3+0.3∗0.50.7∗0.3+0.5∗0.5
= [ 北京 深圳 北京 0.25 0.21 深圳 0.49 0.46 ] =\left[ \begin{matrix} & 北京 & 深圳 \\ 北京 &0.25 & 0.21\\ 深圳 & 0.49 & 0.46\\ \end{matrix} \right] = 北京深圳北京0.250.49深圳0.210.46
结论:在两地移动2次后,如果当前在北京,继续留在北京的概率是0.25,去深圳的概率是0.21.
如果当前在深圳,继续留在深圳的概率是0.46,去北京的概率是0.49
结论
由此可以推断马尔可夫链的三个主要特征是:
- 状态空间:选择范围是有限集
- 无记忆性:预测仅与上一状态相关联
- 转移矩阵:通过矩阵相乘可计算出概率
相关文章:

5分钟理解NPL算法 之 马尔可夫链 Markov Chain
马尔可夫链(Markov Chain) 马尔可夫链是一种简单的推理模型。用于描述受当前事件影响下的下一事件发生概率。在预测学科中广泛应用。例如股票预测、文字推理、路线推荐等。 他的核心思路是:假设事件顺序为: X 1 , X 2 , X 3 , . . . . . X…...

C#_GDI+ 绘图编程入门
官网提供相关API GDI 基本图形功能_drawing 高级二维和矢量图形功能_drawing2D GDI 图像处理功能_Imaging GDI 排版功能_text Windows 窗体应用程序提供打印功能_Printing 像素 构成图像的最小单位就是像素;屏幕上显示不管是位图或者矢量图,当描述…...

自己写一个svg转化为安卓xml的工具类
自己写一个svg转化为安卓xml的工具类_张风捷特烈的博客-CSDN博客 svg资源阿里巴巴矢量资源网站:iconfont-阿里巴巴矢量图标库 感觉一般的svg到Android可用的xml差异有点规律,主要的就是path 秉承着能用代码解决的问题,绝对不动手。能够靠智商解决的问题…...

基于随机森林的机器启动识别,基于随机森林的智能家居电器启动识别
目录 背影 摘要 随机森林的基本定义 随机森林实现的步骤 基于随机森林的机器启动识别 代码下载链接: 基于随机森林的家用电器启动识别,基于RF的电器启动识别,基于随机森林的智能家居启动检测-深度学习文档类资源-CSDN文库 https://download.csdn.net/download/abc991835105/…...
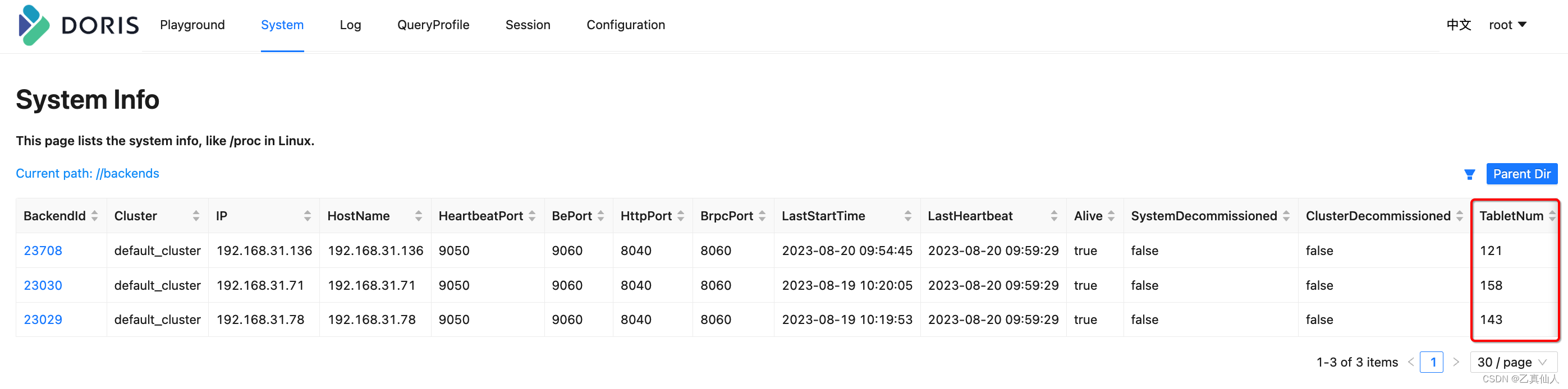
Apache Doris 极简运维之BE扩缩容(1)
Apache Doris 极简运维之BE扩缩容(1) 一、环境信息硬件信息软件信息 二、缩容2.1 DROP BACKEND缩容2.2 DECOMMISSION BACKEND缩容2.2.1 缩容前2.2.2 缩容中2.2.3 缩容后 三、扩容3.1 扩容前3.2 扩容中3.3 扩容后 四、总结 一、环境信息 已部署三个BE节点…...

MySQL每日一练--校园教务系统
一丶数据库名称:SchoolDB 二丶数据库表信息:角色信息表 表名: t_role 主键: r_id 序号 字段名称 字段说明 类别 位数 属性 备注 1 r_id 角色编号 int 主键 自动增长 2 r_name_EN 角色名(英…...
9.阿里Sentinel哨兵
1.Sentinel Sentinel(哨兵)是由阿里开源的一款流量控制和熔断降级框架,用于保护分布式系统中的应用免受流量涌入、超载和故障的影响。它可以作为微服务架构中的一部分,用于保护服务不被异常流量冲垮,从而提高系统的稳定…...
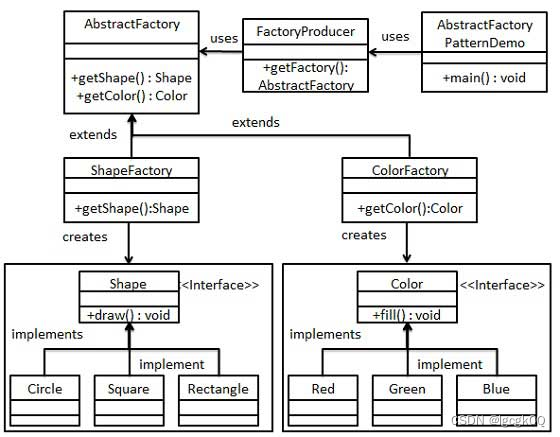
设计模式之工厂方法模式
目录 工厂方法模式 简介 优缺点 结构 使用场景 实现 1.抽象产品 2.具体产品 3.抽象工厂 4.具体工厂 5.调用 总结 抽象工厂模式 简介 结构 实现 区别 工厂方法模式 简介 提供一个用于创建对象的接口(工厂接口),让其实现类(工厂实现类)决定实例化哪…...

【案例教程】基于R语言的物种气候生态位动态量化与分布特征模拟
在全球气候快速变化的背景下,理解并预测生物种群如何应对气候变化,特别是它们的地理分布如何变化,已经变得至关重要。利用R语言进行物种气候生态位动态量化与分布特征模拟,不仅可以量化描述物种对环境的需求和适应性,预…...

Moonbeam生态跨链互操作项目汇总
立秋已过,今年的夏天已经接近尾声,即将迎来凉爽的秋天。Moonbeam生态一同以往持续成长,在8月也举办了不少活动、完成集成合作以及协议更新。让我们一同快速了解Moonbeam生态项目近期发生的大小事件吧! Moonwell Moonwell是一个建…...

基于社会群体算法优化的BP神经网络(预测应用) - 附代码
基于社会群体算法优化的BP神经网络(预测应用) - 附代码 文章目录 基于社会群体算法优化的BP神经网络(预测应用) - 附代码1.数据介绍2.社会群体优化BP神经网络2.1 BP神经网络参数设置2.2 社会群体算法应用 4.测试结果:5…...
)
208. 实现 Trie (前缀树)
题目描述 Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。 请你实现 Trie 类: Trie() 初始化前缀树对…...

adb使用总结
adb连接到模拟器 adb devices 打开模拟器,找到设置。 多次点击版本号,切换到开发者模式 搜索进入开发者选项 开启USB调试 此时在终端输入adb devices就连接上了 使用adb查看安卓手机架构 adb shell getprop ro.product.cpu.abi 进入安卓手机的shell …...
go:正确引入自己编写的包(如何在 Go 中正确引入自己编写的包)
前言 目录如下: 具体教程 1. 工作空间(我的是根目录)新建 go.work 文件 文件内容如下: go 1.21.0use (./tuchuang./tuchuang/testm ) 2. 添加go.mod文件 1. 包文件夹下 进入testm目录执行 go mod init testModule 2. 引用目…...
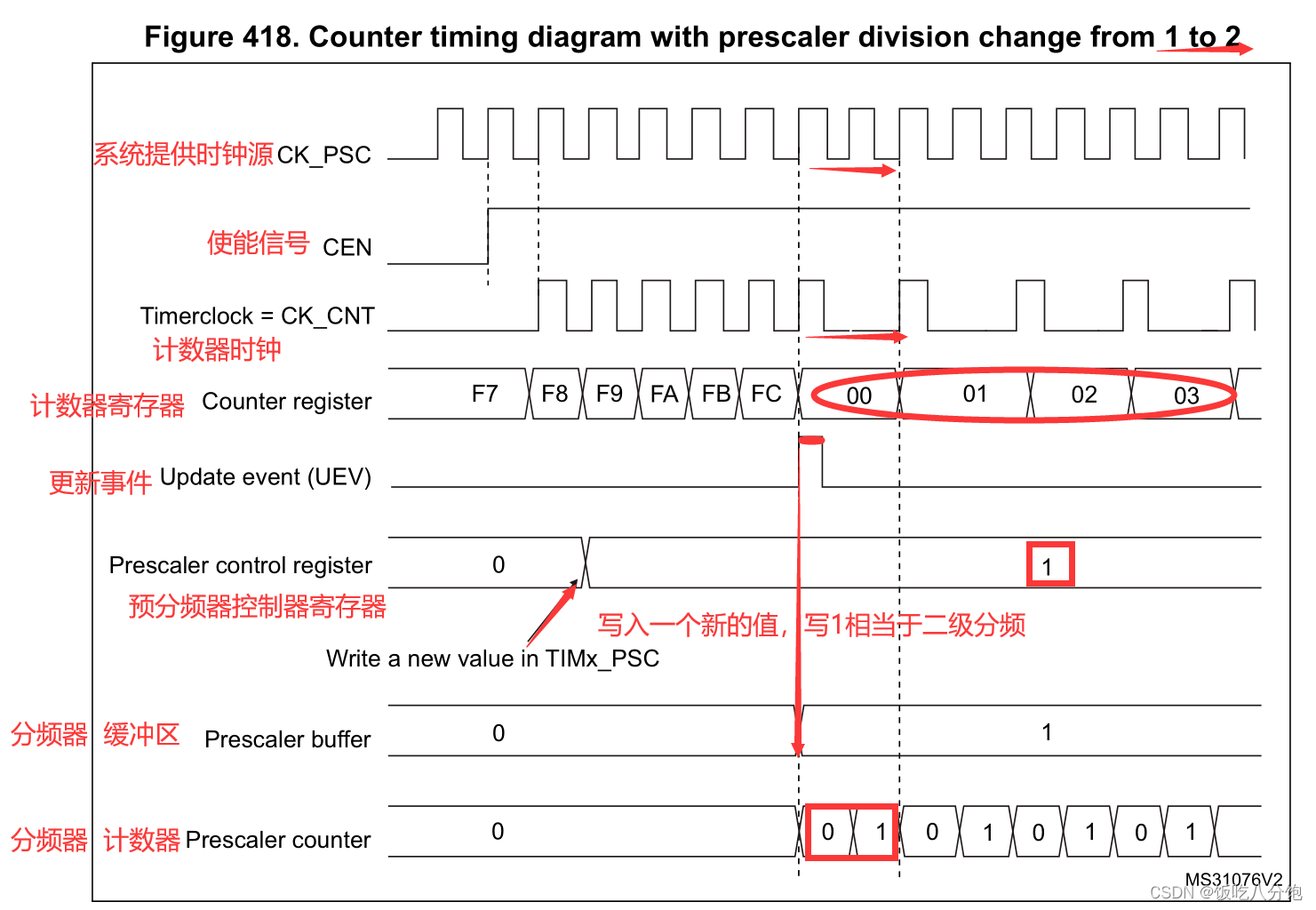
cortex-A7核PWM实验--STM32MP157
实验目的:驱动风扇,蜂鸣器,马达进行工作 目录 一,PWM相关概念 有源蜂鸣器和无源蜂鸣器 二,分析电路图,框图 三,分析RCC章节 1,确定总线连接 2,根据总线内容确定基…...

电工-学习电工有哪些好处
学习电工有哪些好处?在哪学习电工? 学习电工有哪些好处?在哪学习电工?学习电工可以做什么?优势有哪些? 学习电工可以做什么?学习电工有哪些好处? 就业去向:可在企业单位…...

Redis内存空间预估与内存优化策略:保障数据安全与性能的架构实践AIGC/AI绘画/chatGPT/SD/MJ
推荐阅读 AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI绘画、AI讲话、翻译,GPU点亮AI想象空间 资源分享 「java、python面试题」来自UC网盘app分享,打开手机app,额外获得1T空间 https://dr…...

Pandas数据分析教程-数据处理
pandas-02-数据清洗&预处理 B. 数据处理1. 重复值处理2. map逐元素转换3. 值替换4. 改变索引值5. 离散化与分箱6. 检测过滤异常值7. 排列与随机采样8. 根据类别生成one-hot向量,向量化文中用S代指Series,用Df代指DataFrame 数据清洗是处理大型复杂情况数据必不可少的步骤…...

php 多维数组排序,根据某一列排序(array_multisort()和array_column()联用)
array_multisort()和array_column()联用效果直接叠满,11>100 先来看下两个函数的介绍和用法 array_column(): 一般模式,不需要其中字段作为id,只需要提取val值 <?php // 可能从数据库中返回数组 $a [[id > 5698, first_name > Peter, last_name > G…...
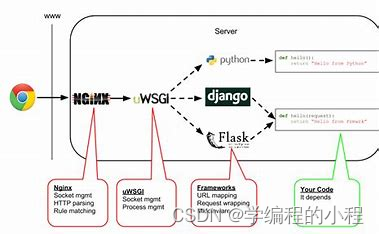
框架分析(5)-Django
框架分析(5)-Django 专栏介绍Django核心概念以及组件讲解模型(Model)视图(View)模板(Template)路由(URLconf)表单(Form)后台管理&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
