718. 最长重复子数组
718. 最长重复子数组
- 原题链接:
- 完成情况:
- 题解:
- 方法一:动态规划
- 方法二:滑动窗口
- 方法三:二分查找 + 哈希
原题链接:
718. 最长重复子数组
https://leetcode.cn/problems/maximum-length-of-repeated-subarray/description/
完成情况:
题解:
方法一:动态规划

package 西湖算法题解___中等题;public class __718最长重复子数组__动态规划 {//子数组的话,默认是连续的。public int findLength(int[] nums1, int[] nums2) {/*给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。当然了,肯定是要求顺序,而非连续。那么必然就需要用到动态数组,采取累积的形式*/int n = nums1.length,m = nums2.length;int dp_findLength [][] = new int[n+1][m+1];int res = 0;for (int i=n-1;i>=0;i--){for (int j=m-1;j>=0;j--){dp_findLength[i][j] = (nums1[i] == nums2[j] ? dp_findLength[i+1][j+1] + 1:0);res = Math.max(res,dp_findLength[i][j]);}}return res;}
}方法二:滑动窗口
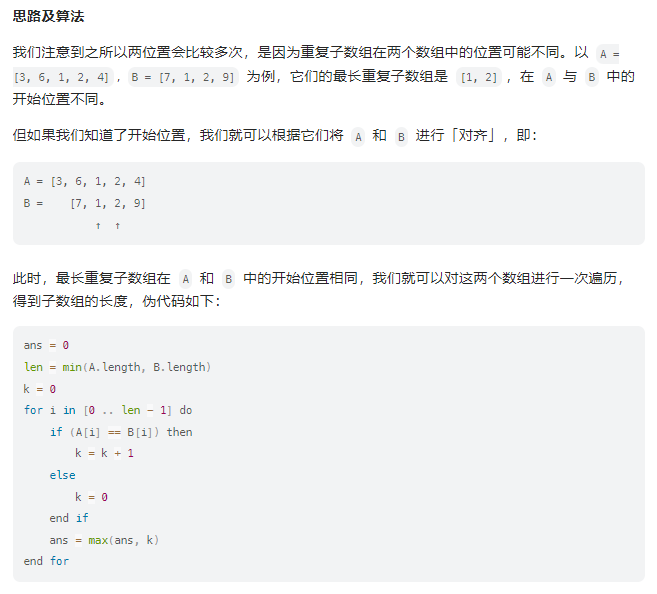

package 西湖算法题解___中等题;public class __718最长重复子数组__滑动窗口 {public int findLength(int[] nums1, int[] nums2) {int n = nums1.length,m = nums2.length;int res = 0;for (int i=0;i<n;i++){int len = Math.min(m,n-i);int maxLen = maxLength(nums1,nums2,i,0,len);res = Math.max(res,maxLen);}for (int i=0;i<m;i++){int len = Math.min(n,m-i);int maxLen = maxLength(nums1,nums2,0,i,len);res = Math.max(res,maxLen);}return res;}private int maxLength(int[] nums1, int[] nums2, int addA, int addB, int len) {int res = 0,k=0;for (int i=0;i<len;i++){if (nums1[addA+i] == nums2[addB+i]){k++;}else {k=0;}res = Math.max(res,k);}return res;}
}方法三:二分查找 + 哈希

package 西湖算法题解___中等题;import java.util.HashSet;
import java.util.Set;public class __718最长重复子数组__二分查找_哈希表 {int mod = 1000000009;int base = 113;public int findLength(int[] nums1, int[] nums2) {int left = 1,right = Math.min(nums1.length,nums2.length)+1;while (left < right){int mid = (left + right) >> 1;if (myCheck(nums1,nums2,mid)){left = mid +1;}else {right = mid;}}return left - 1;}private boolean myCheck(int[] A, int[] B, int len) {long hashA = 0;for (int i=0;i<len;i++){hashA = (hashA * base + A[i]) % mod;}Set<Long> bucketA = new HashSet<Long>();bucketA.add(hashA);long mult = qPow(base,len - 1);for (int i = len;i < A.length;i++){hashA = ((hashA - A[i - len] * mult % mod + mod) % mod * base + A[i]) % mod;bucketA.add(hashA);}long hashB = 0;for (int i=0;i<len;i++){hashB = (hashB * base +B[i])%mod;}if (bucketA.contains(hashB)){return true;}for (int i=len;i<B.length;i++){hashB = ((hashB - B[i - len] * mult % mod + mod) % mod * base + B[i]) % mod;if (bucketA.contains(hashB)){return true;}}return false;}/*** 使用快速幂计算x^n % mod 的值* @param x* @param n* @return*/private long qPow(long x, long n) {long res = 1L;while (n != 0){if ((n&1) != 0){res = res * x % mod;}x = x*x % mod;n >>= 1;}return res;}
}相关文章:

718. 最长重复子数组
718. 最长重复子数组 原题链接:完成情况:题解:方法一:动态规划方法二:滑动窗口方法三:二分查找 哈希 原题链接: 718. 最长重复子数组 https://leetcode.cn/problems/maximum-length-of-repe…...

Mysql join加多条件与where的区别
最近在项目中遇到一个问题,感觉有点意思,在解决问题及查阅了相关资料后,打算写篇文章给朋友们分享一下。 问题现象: 问题是很常见的空指针问题,后端查询数据库数据,遍历进行相关业务处理时报空指针。通过…...

div滚动条自动滚动到底部
<div id"center"></div>// 滚动条到最底部scrollToBottom(){var box document.getElementById(center);this.$nextTick(() > {box.scrollTop box.scrollHeight})},...
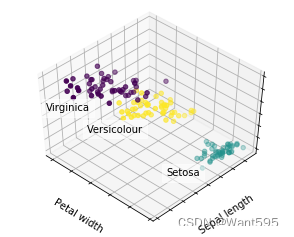
【深度学习】实验02 鸢尾花数据集分析
文章目录 鸢尾花数据集分析决策树K-means 鸢尾花数据集分析 决策树 # 导入机器学习相关库 from sklearn import datasets from sklearn import treeimport matplotlib.pyplot as plt import numpy as np# Iris数据集是常用的分类实验数据集, # 由Fisher, 1936收集…...

AI大模型潮水中,医疗数字化加速「求解」
蝴蝶挥动翅膀,医疗行业每个角落开始连锁反应,曾经被忽视的问题也愈发明显。但与之对应的是,对数字化和AI大模型的价值认可,在中国医疗赛道也正在加速来临。 作者|斗斗 编辑|皮爷 出品|产业家 重庆市某地方人民医院…...
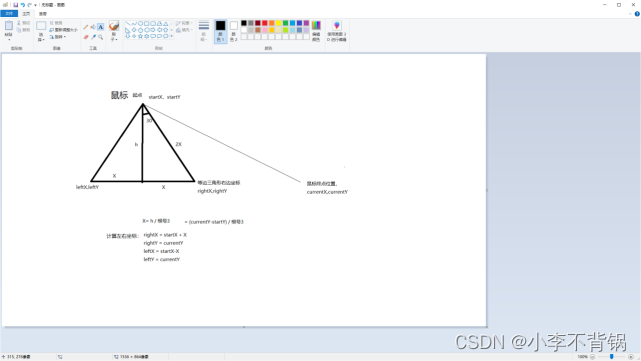
【安卓】自定义View实现画板涂鸦等功能
一、实现效果 二、代码 1、MainActivity.class package com.lsl.mydrawingboarddemo;import androidx.appcompat.app.AppCompatActivity; import androidx.core.content.ContextCompat;import android.os.Bundle; import android.os.Handler; import android.view.View; impo…...

面试题. 搜索旋转数组
搜索旋转数组。给定一个排序后的数组,包含n个整数,但这个数组已被旋转过很多次了,次数不详。请编写代码找出数组中的某个元素,假设数组元素原先是按升序排列的。若有多个相同元素,返回索引值最小的一个。 示例1: 输入…...
前端需要理解的数据治理与异常监控知识
1 数据治理 前端数据治理的重要指标是准确性和数据,一个数据对象包括数据值和其他元数据。 2 数据上报方式 2.1 Image 通过将采集的数据拼接在图片请求的后面,向服务端请求一个 1*1 px 大小的图片(gif)实现的,设置…...
hook 后的开始 一)
ip_vs 原理解析 (四)hook 后的开始 一
文章目录 ip_vs hook 后NF_INET_LOCAL_IN 本章重点: k8s 如何利用 ip_vs 实现源 IP 会话亲和性。 ip_vs hook 后 NF_INET_LOCAL_IN 根据优先级依次是 ip_vs_reply4,ip_vs_remote_request4 ip_vs_reply4| -- ip_vs_out| -- skb_to_full_sk(skb…...
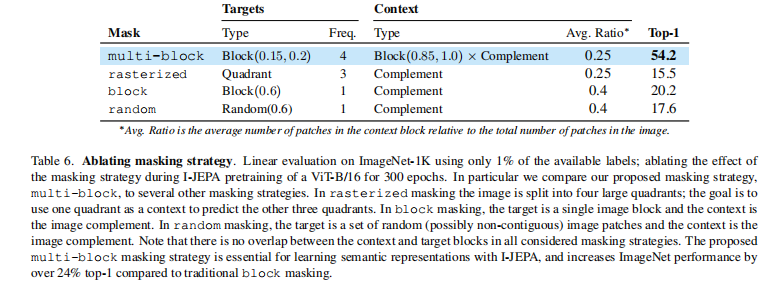
【论文解读】基于图的自监督学习联合嵌入预测架构
一、简要介绍 本文演示了一种学习高度语义的图像表示的方法,而不依赖于手工制作的数据增强。论文介绍了基于图像的联合嵌入预测架构(I-JEPA),这是一种用于从图像中进行自监督学习的非生成性方法。I-JEPA背后的idea很简单ÿ…...

C++ 容器
string 1. 构造 string s1(); // 1 string s2("hello"); // hello string s3(3, k); // kkk string s4("hellohello", 2, 4); // lloh2. 赋值 string s1 "hellohello"; // hellohello string s2.assign(s1); // he…...

【PHP】PHP文件操作详解
PHP是一种广泛使用的服务器端脚本语言,用于开发Web应用程序。在PHP中,文件操作是一项重要的功能,包括文件的读取、写入、删除和其他操作。本文将详细介绍PHP文件操作的各个方面,并通过示例代码进行说明。 一、文件读取 要读取一…...

硬核旗舰南卡OE CC开放式耳机发布,重新定义百元开放式耳机新标杆!
随着现在健康意识的不断提高,人们对于日常用品的要求越来越高,在耳机市场中,健康因素也逐渐成为消费者所考虑的因素之一,入耳式耳机因为会引发中耳炎、耳膜炎等疾病,正在逐渐被开放式蓝牙耳机所取代,南卡…...
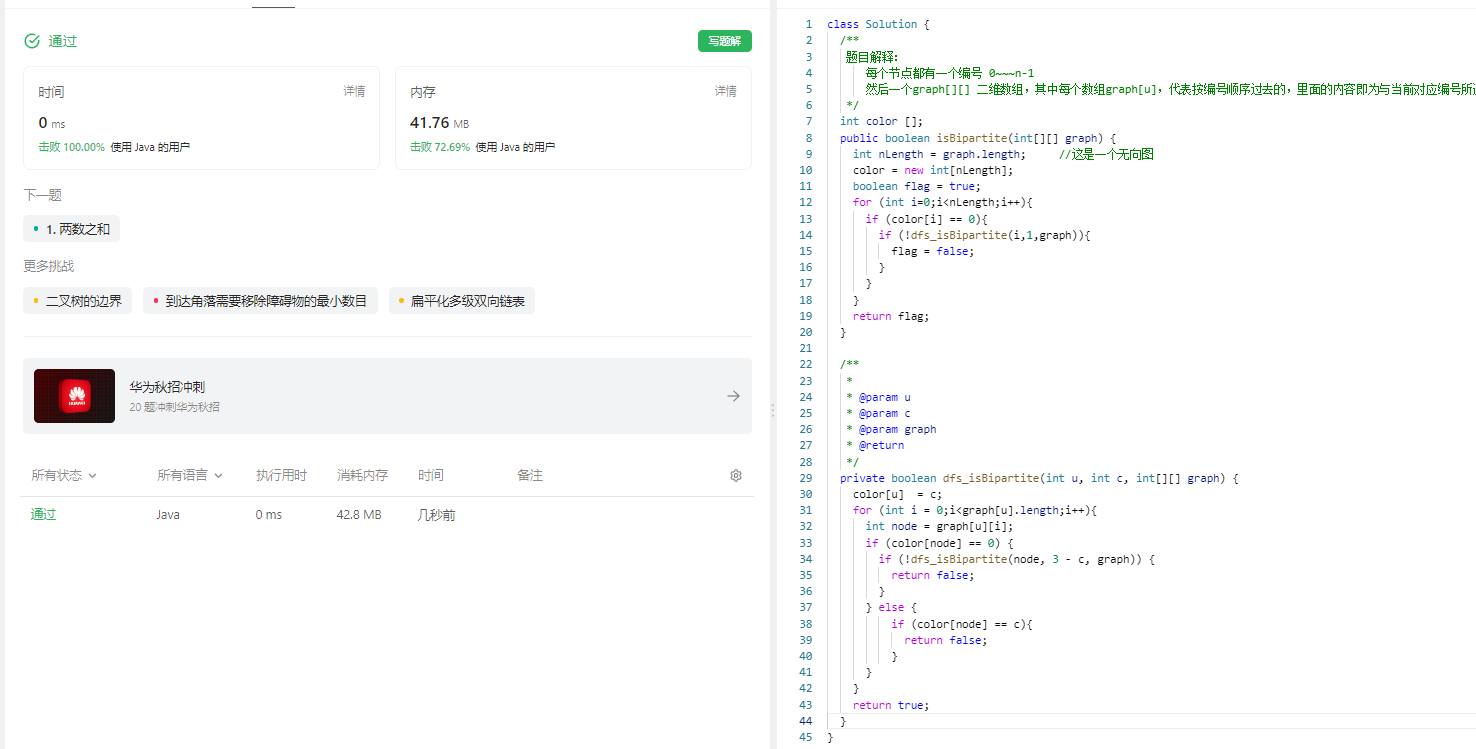
785. 判断二分图
785. 判断二分图 原题链接:完成情况:解题思路:参考代码: 原题链接: 785. 判断二分图 https://leetcode.cn/problems/is-graph-bipartite/description/ 完成情况: 解题思路: 题目解释&#x…...

限时 180 天,微软为 RHEL 9 和 Ubuntu 22.04 推出 SQL Server 2022 预览评估版
导读近日消息,微软公司今天发布新闻稿,宣布面向 Red Hat Enterprise Linux(RHEL)9 和 Ubuntu 22.04 两大发行版,以预览模式推出 SQL Server 2022 评估版。 近日消息,微软公司今天发布新闻稿,宣布…...

一款ccm的功率因素校正控制器ncp1654
产品概述: NCP1654是用于连续传导模式的控制器(CCM)功率因数校正升压预转换器。它控制固定频率模式下的电源开关导通时间(PWM)并且取决于瞬时线圈电流。 该电路封装在SO8封装中,最大限度地减少了外部组件&a…...

4.若依框架上传文件
1.服务端代码-控制器 /*** 上传文件*/PostMapping("/upload")Operation(summary "上传")public AjaxResult uploadFile(MultipartFile file) throws Exception {try {// 上传文件路径String filePath RuoYiConfig.getUploadPath();// 上传并返回新文件名…...
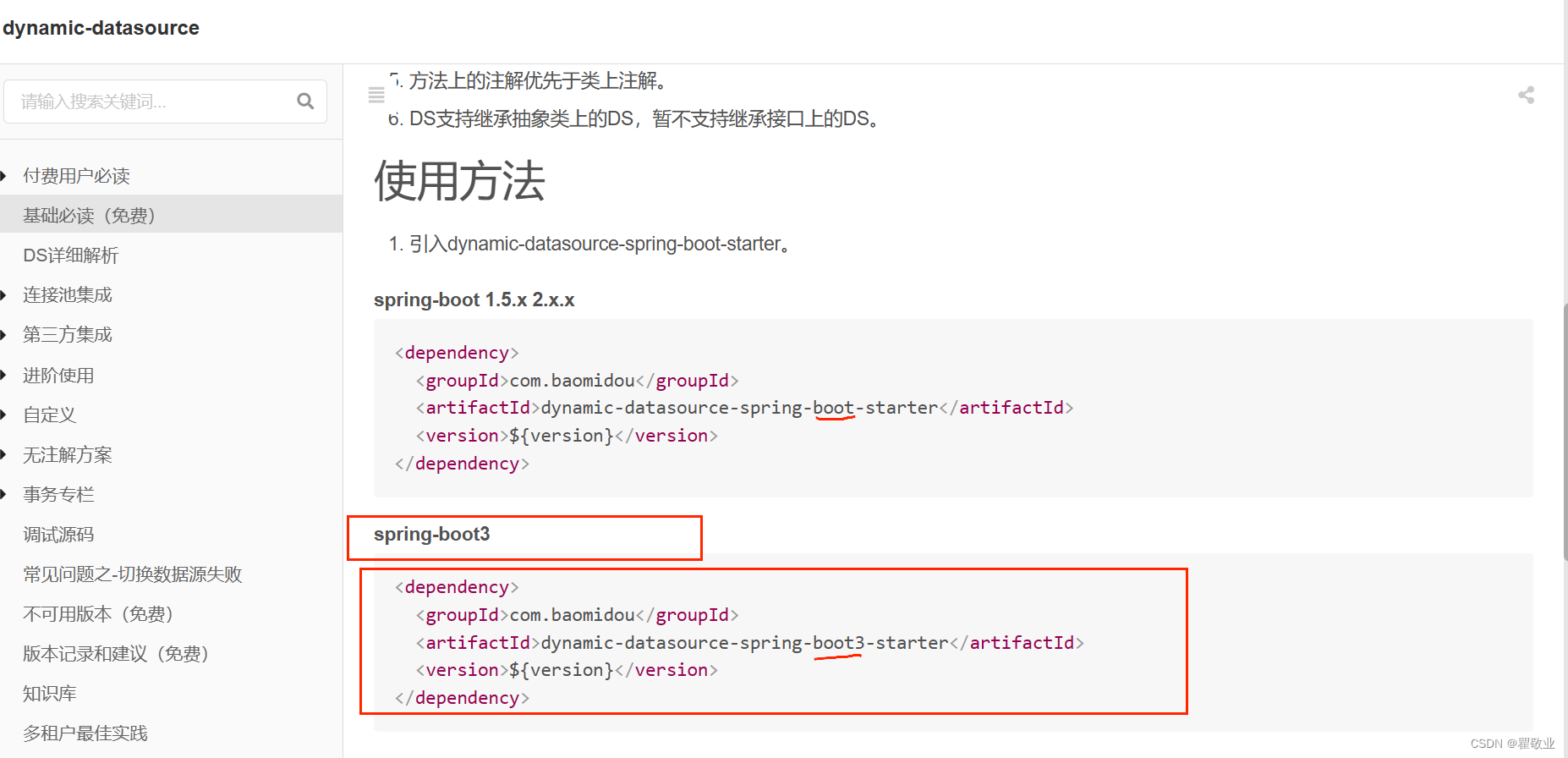
Property ‘sqlSessionFactory‘ or ‘sqlSessionTemplate‘ are required
项目场景: 最近因为公司业务需要在搭一个新架构,用的springboot3和jdk17,在整合mybatis多数据源的时候报错 (引用的mybatisplus 和 mybatisplusjion的是最新的包-2023-08-26) Error creating bean with name ‘XXXServiceImpl’:…...
idea的debug断点的使用
添加断点(目前不知道如何添加断点,就给AutoConfigurationImportSelector的每个方法都加上断点): 然后将StockApplication启动类以debug方式运行,然后程序就会停在119行 点击上边的step over让程序往下运行一行&#x…...

【UE】蓝图通信——事件分发器
目标 比如我现在希望点击控件蓝图A中的按钮后,蓝图B能够马上做出响应 实现步骤 1. 这里控件蓝图A叫“UI_按钮”,我在该蓝图中创建了一个名为“btnIsClicked”的事件分发器 当按钮被点击时,就会调用“btnIsClicked” 2. 蓝图B这里叫做“BP_…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
