最长不含重复字符的子字符串
今天处理一道算法题目,《剑指Offer》第48题,力扣中等题。
这道题也是面试的高频题!
题目描述
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
示例1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
解题思路
方法1:动态规划
用f(i)表示以第i个字符为结尾的不含重复字符的最长长度,推断出三种情况:
1. 如果当前字符在之前都没出现过,那么f(i) = f(i-1) + 1;
2. 如果当前字符在之前出现过,并且两者的距离差d<=f(i-1),那么当前的最长长度即为d;
3. 如果当前字符在之前出现过,并且两者的距离差d>f(i-1),那么说明之前的这个元素已经在滑动窗口之外,我们仍然可以用f(i) = f(i-1)+1;
/*** 动态规划*设f(i)表示以第i个字符为结尾的不含重复字符的最长长度,可以得到状态转换方程:f(i)={f(i-1)+1; 第i个字符之前没出现过d; 之前出现过,但和之前出现的字符距离差d小于等于f(i-1),即d<f(i-1)f(i-1)+1; 之前出现过,且d>f(i-1)}// 以arabcacfr为例,在计算最后一个r,即f(8)的时候,出现d>f(7)的情况,可以把r追加到f(7)的后面这个思路是最通俗易懂的,但代码和时间上不是最优的* @param s* @return*/public int lengthOfLongestSubstring(String s) {if(s == null || s.length() == 0)return 0;int n = s.length();if(n == 1)return 1;int[] mem = new int[n];Map<Character, Integer> map = new HashMap<>();//初始化mem[0] = 1;map.put(s.charAt(0), 0);for(int i = 1; i < n; ++i) {char c = s.charAt(i);//之前没有出现过,则f(i) = f(i-1)+1if(!map.containsKey(c)) {map.put(c, i);mem[i] = mem[i-1] + 1;}else{//之前出现过,记录差值d,并比较差值和f(i-1)的大小int before = map.get(c);int d = i - before;if(d <= mem[i-1]) {mem[i] = d;}else {mem[i] = mem[i-1]+1;}//最后记得更新这个值map.put(c, i);}}int maxLen = 0;for(int i = 0; i < n; ++i) {maxLen = Math.max(maxLen, mem[i]);}return maxLen;}总体来说,这种方法时间不是最优,但思路很清晰。
方法2:滑动窗口
用i,j两个指针来控制窗口的左右边界,然后用i每次递增一隔,计算以i为起点的最长无重复子串,只是这里的j不用从i的位置开始,这种做法也是力扣官方的做法,个人觉得不太好,时间复杂度不高。
/*** 滑动窗口(或者就左右指针)* @param s* @return*/public int lengthOfLongestSubstring2(String s) {//abcabcbbif(s == null || s.length() == 0)return 0;int n = s.length();if(n == 1)return 1;Set<Character> set = new HashSet<>();int i = 0;set.add(s.charAt(0));int j = 1;int maxLen = 0;while(i < n) {while(j < n) {char c = s.charAt(j);if(set.contains(c)){break;}set.add(c);j++;}maxLen = Math.max(maxLen, j-i);set.remove(s.charAt(i));i++;}return maxLen;}方法3:左右指针
该方法是极力推荐的做法:用j遍历字符串,每次判断以j为结尾的最长无重复字符的子串长度,如果出现了重复字符,则更新左边界。只是这里,需要额外注意,更新左边界的时候,需要取上一个左边界和当前元素对应的之前值的最大值。
/*** 左右指针,j表示以第j个字符为结尾的不含重复字符的最长子串* 这里必须要注意一种情况,就是左边界需要取原左边界和当前元素在map中保存的值的最大值* 防止类似于abba这种字符串* @param s* @return*/public int lengthOfLongestSubstring3(String s) {if (s == null || s.length() == 0)return 0;int n = s.length();int i = -1;int maxLen = 0;Map<Character, Integer> map = new HashMap<>();for (int j = 0; j < n; ++j) {if (map.containsKey(s.charAt(j))) {i = Math.max(i, map.get(s.charAt(j)));}map.put(s.charAt(j), j);maxLen = Math.max(maxLen, j - i);}return maxLen;}相关文章:

最长不含重复字符的子字符串
今天处理一道算法题目,《剑指Offer》第48题,力扣中等题。 这道题也是面试的高频题! 题目描述 请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。 示例1: 输入: "abcabcbb" …...

git中git push origin master推送远程操作失败,报错解决方案
报错图片如下所示: 解决方案: 使用下面代码进行本地与远程仓库的链接: git remote add origin http://xxxxx///xxx(https://gitee.com/peach-fog/shopping-cart-car-warehouse.git)链接完成之后就会输出:fatal: remote origin already exists. 链接完成之后就需要使用git br…...
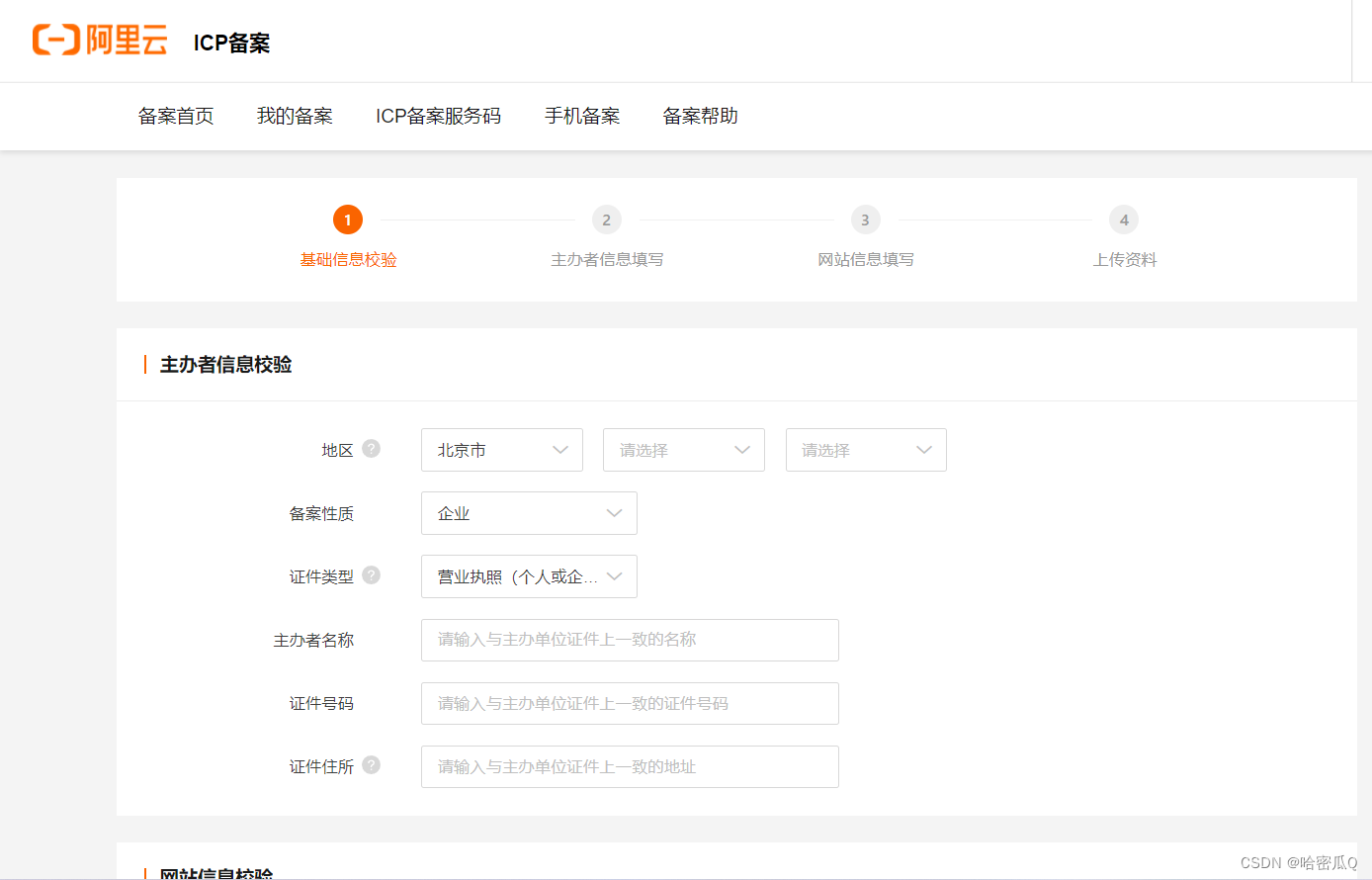
服务器部署流程与经验记录
服务器部署流程1.项目部署1.1 重置实例密码1.2 配置安全组规则1.3 远程连接服务器1.4 安装所需软件1.5 安装Tomcat1.6 配置宝塔安全组1.7 导入数据库和项目2. 域名注册3. 网站备案1.项目部署 1.1 重置实例密码 1.2 配置安全组规则 1.3 远程连接服务器 使用VNC远程连接&#…...

超火的情感视频短视频账号,赚钱的路子有多野?
目录 一、情感类视频内容模式 1、线上情感导师型 2、用动画传达人生哲理 3、网抑云式的野生“文案馆” 4、星座式情感账号 二、情感号变现方式 1、首先是可以接广告 2、收徒做情感号培训,知识付费 3、导流粉丝到公众号 4、通过卖号来变现 6、导流微信变现…...

Linux系列 linux 常用命令(笔记)
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 座右铭:低头赶路,敬事如仪 个人主页:网络豆的主页 目录 前言 一.linux 常用命令(目录文和件基本操作) 1.命令的分类…...

Cosmos 基础教程(二)-- Run a Node, API, and CLI
有很多不同的方法来运行Cosmos区块链的节点。您将探索如何使用simapp 进行此操作。 1、编译simapp Cosmos SDK存储库包含一个名为 simapp 的文件夹。在这个文件夹中,您可以找到运行Cosmos SDK模拟版本的代码,这样您就可以在不实际与链交互的情况下测试…...

C# 读写xml文件总结 [详细]
C# 读写xml文件总结C#写入xml文件1、XmlDocument2、DataSet对象里的值来生成XML文件3、利用XmlSerializer来将类的属性值转换为XML文件的元素值。示例:写入xml1、创建xml文档2 、增加节点3 、修改节点:4 、删除节点c#读取xml文件C#写入xml文件 1、XmlDo…...

【Java基础】IO流
IO流 最后一定要关闭流,防止资源泄露 字节流 一次读取1字节,8比特 FileInputStream import org.junit.jupiter.api.Test;import java.io.FileInputStream; import java.io.FileOutputStream; import java.io.IOException;public class CopyBytes {pub…...
)
Boolean,Array,Object数据类型(回顾)
Boolean数据类型范围Boolean(value)Object数据类型特点键值对数组特点类数组特点 Boolean数据类型范围 true,false 链接 Boolean(value) 定义:其他类型转布尔类型 六大假值:false,undefined,null,NaN,0…...

Python常见的数据类型
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...

欠缺知识点罗列
UML五种关系的特点 依赖,关联,组合,聚合,泛化。认识UML类关系——依赖、关联、聚合、组合、泛化 - 腾讯云开发者社区-腾讯云 数据结构- 生成树的定义。 每周学点大数据 | No.17最小生成树 - 腾讯云开发者社区-腾讯云 有向图。 …...

基于springboot+vue的校园社团管理系统(前后端分离)
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

你了解互联网APP推荐的背后逻辑么(下)?
上篇重点介绍了互联网APP在搜索交互场景下的通用逻辑,让大众对每天离不开的搜索进行了一个普遍介绍。这一篇,我们来聊聊抖音、头条等APP划一划这个动作背后,是怎么做推荐的。推荐的背后,离不开每个用户的数据,而且这个…...
总是跳转到国内版(cn.bing.com)?New Bing使用全攻略
你是否想要使用强大的(被削后大嘘)New Bing? 你是否已经获得了New Bing的使用资格? 你是否在访问www.bing.com/new时提示页面不存在? 你是否在访问www.bing.com时总是重定向到cn.bing.com而使用不了New Bing? New Bi…...
神经网络的基本骨架—nn.Module使用
一、pytorch官网中torch.nn的相关简介可以看到torch.nn中有许多模块:二、Containers模块1、MODULE(CLASS : torch.nn.Module)import torch.nn as nn import torch.nn.functional as Fclass Model(nn.Module):#nn.Module---所有神经网络模块的…...

面试官:你是怎样进行react组件代码复用的
mixin Mixin 设计模式 Mixin(混入)是一种通过扩展收集功能的方式,它本质上是将一个对象的属性拷贝到另一个对象上面去,可以拷贝多个属性到一个对象上,为了解决代码复用问题。 常用的方法:JQuery 的 exte…...
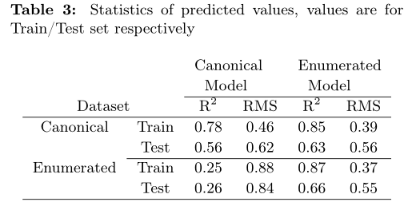
arxiv2017 | 用于分子神经网络建模的数据增强 SMILES Enumeration
论文标题:SMILES Enumeration as Data Augmentation for Neural Network Modeling of Molecules论文地址:https://arxiv.org/abs/1703.07076代码地址:https://github.com/Ebjerrum/SMILES-enumeration一、摘要摘要中明显提出:先指…...
)
倒计时2天!TO B人的传统节日,2023年22客户节(22DAY)
去年,2022.02.22,正月二十二星期二,在这个最多2的一天,成功举办了“首届22客户节(22DAY)”,一群To B互联网人相约杭州见证; 癸卯兔年,2023.02.22,让我们再度…...

java版工程管理系统Spring Cloud+Spring Boot+Mybatis实现工程管理系统源码
java版工程管理系统Spring CloudSpring BootMybatis实现工程管理系统 工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和…...
:142环形链表II、242有效的字母异位词、383赎金信、349两个数组的交集)
数据结构刷题(六):142环形链表II、242有效的字母异位词、383赎金信、349两个数组的交集
1.环形链表II题目链接思路:设置快慢双指针注意:(1)是否有环(快慢双指针是否能碰面也就是相等)(2)环形入口的判断。从头结点出发一个指针,从相遇节点 也出发一个指针&…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
: 一刀斩断视频片头广告)
快刀集(1): 一刀斩断视频片头广告
一刀流:用一个简单脚本,秒杀视频片头广告,还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农,平时写代码之余看看电影、补补片,是再正常不过的事。 电影嘛,要沉浸,…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...
