C++二叉树进阶
本期内容我们讲解二叉树的进阶知识,没有看过之前内容的小伙伴建议先看往期内容
二叉树-----补充_KLZUQ的博客-CSDN博客
目录
二叉搜索树
代码实现
基础框架
Insert
Find
Erase
析构函数
拷贝构造
赋值
二叉搜索树的应用
全部代码
二叉搜索树
二叉搜索树又称二叉排序树,它或者是一棵空树 ,或者是具有以下性质的二叉树 :若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树
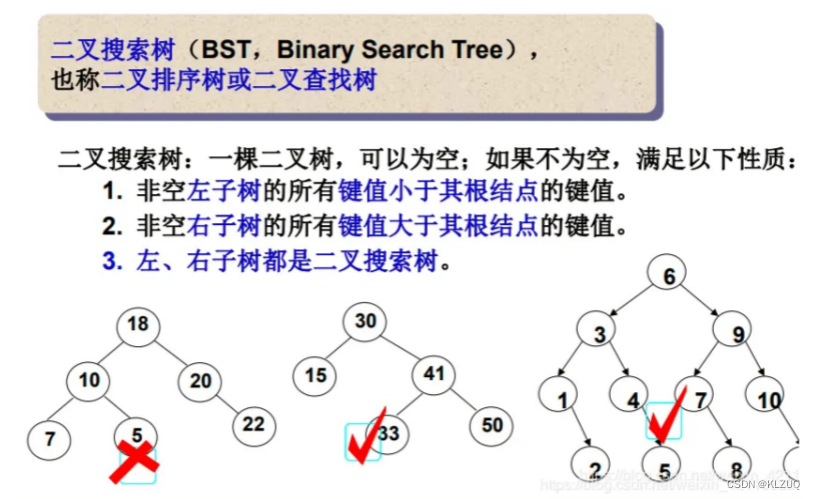
由于结构特性,二叉搜索树很适合查找数据,那它最多查找多少次呢?高度次吗?

其实不是的,二叉搜索树是可能会有右边这种情况的,时间复杂度是O(N)
这其实是不好的,后面我们会讲AVL树和红黑树,他们的时间复杂度是O(longN)
话不多说,下面我们来实现二叉搜索树
代码实现
基础框架
template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr),_key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:BSTree():_root(nullptr){}bool Insert(const K& key){}
private:Node* _root;
};我们先写出基本框架,接着我们来实现插入
Insert

假设我们有这样一棵树,我们要插入11,13和16,该怎么办呢?我们将11和root节点对比,11比8大,应该在右边,继续对比11和10,比10大,在右边,11比14小,在左边,比13小,在左边
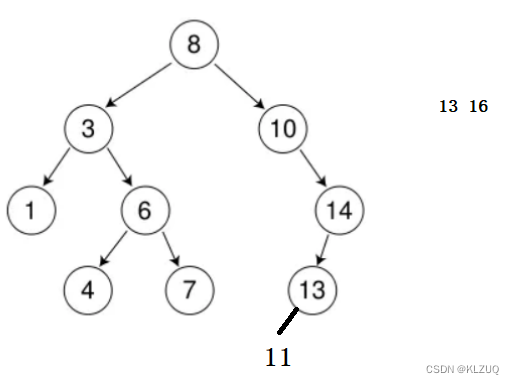
就成了这个样子,再看13,我们对比后发现树里面已经有13了,所以插入失败,最后看16,16比14大,链接在14的右边即可
bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else {return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else {parent->_left = cur;}return true;}我们先用循环来实现
下面为了测试,我们写一个中序遍历
void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == NULL){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}我们写成子函数是因为我们在调用时还得传root,比如封装写成子函数,这样我们就不用传了,下面进行测试
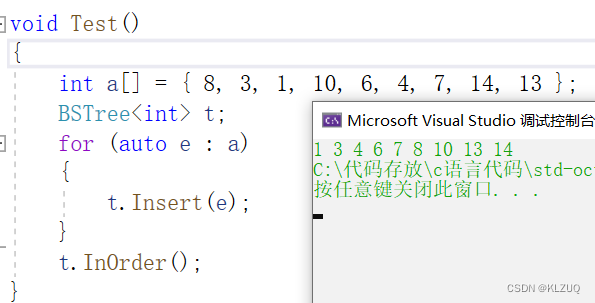
没有问题,中序遍历出来是有序的
bool InsertR(const K& key){return _InsertR(_root, key);}
private:bool _InsertR(Node*& root, const K& key){if (root == nullptr)//因为引用,所以下面可以直接new{root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _InsertR(root->_left, key);}else{return false;}}我们再看递归版本的,递归版本里参数加了引用,这个引用可以让我们在插入节点时不用找该节点的父亲节点,可谓是神之一手
Find
bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}find也非常简单
bool FindR(const K& key){return _FindR(_root, key);}
private:bool _FindR(Node* root,const K& key)//递归版本{if (root == nullptr){return false;}if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return true;}}还有递归版本的,我们再把子函数写成私有的
Erase

删除是一个重点,我们有这样一棵树,假设我们要删除7,14和3
7是叶子节点,删除后再把6的右置为空即可,14也还好说,它只有一个孩子,我们可以让10的右节点指向13,最麻烦的是3,我们该如何删除3呢?这里就要用到替换法,用3的左子树的最大节点或者右子树的最小节点来替换,一棵树的最大节点是这棵树的最右边的节点,所以左子树的最大节点很好找,最小的节点就是最左边的,所以右子树的最小节点也很好找
bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//找到了{//左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}} }//右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else {if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}} }//左右都不为空else{//找替代节点Node* parent = cur;//这里不能给空,防止leftMax是根节点的左子树的第一个节点Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_left;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur = leftMax;}delete cur;return true;}}return false;}删除要考虑的情况非常多,大家一定要画图才能理解

大家用这几张图画一画,结合代码,里面的坑是非常多的
下面我们测试一下

没有问题,大家测试时再把整棵树删空测试一下
bool EraseR(const K& key){return _EraseR(_root, key);}
private:bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;if (root->_left == nullptr)//左为空{root = root->_right;//因为引用所以可以直接改}else if (root->_right == nullptr)//右为空{root = root->_left;}else //左右都不为空{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;return true;}}我们再看递归版本,这里同样使用了引用,可以方便很多,大家画图对照一下就可以理解
下面我们再完成一下析构函数
析构函数
~BSTree(){Destroy(_root);}
void Destroy(Node*& root){if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}也是同样使用引用,为了方便置空
拷贝构造
BSTree(const BSTree<K>& t){_root = Copy(t._root);}
Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* copyroot = new Node(root->_key);copyroot->_left = Copy(root->_left);copyroot->_right = Copy(root->_right);return copyroot;}拷贝构造这里是不能调用insert的,因为任何顺序的插入都不能保证和原来树的一样,大家可以试一试,而我们这样写拷贝构造就可以解决问题
赋值
BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}赋值的话我们直接用现代写法即可
二叉搜索树的应用
1. K 模型: K 模型即只有 key 作为关键码,结构中只需要存储 Key 即可,关键码即为需要搜索到 的值 。比如: 给一个单词 word ,判断该单词是否拼写正确 ,具体方式如下:以词库中所有单词集合中的每个单词作为 key ,构建一棵二叉搜索树在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。2. KV 模型:每一个关键码 key ,都有与之对应的值 Value ,即 <Key, Value> 的键值对 。该种方式在现实生活中非常常见:比如 英汉词典就是英文与中文的对应关系 ,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文 <word, chinese> 就构成一种键值对;再比如 统计单词次数 ,统计成功后,给定单词就可快速找到其出现的次数, 单词与其出现次数就是 <word, count> 就构成一种键值对 。
下面我们修改我们上面的程序,把它变成KV的
template<class K, class V >struct BSTreeNode{BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key),_value(value){} };template<class K,class V>class BSTree{typedef BSTreeNode<K,V> Node;public:BSTree():_root(nullptr){}void InOrder(){_InOrder(_root);cout << endl;}Node* FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key, const V& value){return _InsertR(_root, key,value);}bool EraseR(const K& key){return _EraseR(_root, key);}private:bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;if (root->_left == nullptr)//左为空{root = root->_right;//因为引用所以可以直接改}else if (root->_right == nullptr)//右为空{root = root->_left;}else //左右都不为空{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key,const V& value){if (root == nullptr)//因为引用,所以下面可以直接new{root = new Node(key,value);return true;}if (root->_key < key){return _InsertR(root->_right, key,value);}else if (root->_key > key){return _InsertR(root->_left, key,value);}else{return false;}}Node* _FindR(Node* root, const K& key)//递归版本{if (root == nullptr){return nullptr;}if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return root;}}void _InOrder(Node* root){if (root == NULL){return;}_InOrder(root->_left);cout << root->_key << ":"<<root->_value<<endl;_InOrder(root->_right);}private:Node* _root;};这里我删除了一些,下面我们来进行测试
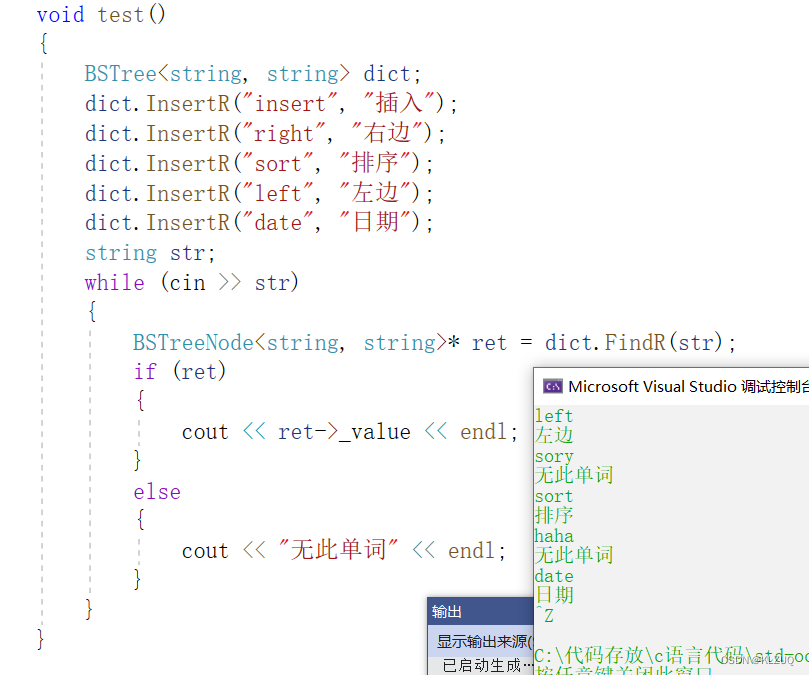
这里我们模拟一个字典
还有统计水果出现的次数,没有出现的水果我们存进去,出现的让value++
全部代码
namespace key
{template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:BSTree():_root(nullptr){}BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}~BSTree(){Destroy(_root);}bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//找到了{//左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}//右为空else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}}//左右都不为空else{//找替代节点Node* parent = cur;//这里不能给空,防止leftMax是根节点的左子树的第一个节点Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_left;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur = leftMax;}delete cur;return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}bool FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key){return _InsertR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}private:Node* Copy(Node* root){if (root == nullptr){return nullptr;}Node* copyroot = new Node(root->_key);copyroot->_left = Copy(root->_left);copyroot->_right = Copy(root->_right);return copyroot;}void Destroy(Node*& root){if (root == nullptr){return;}Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;if (root->_left == nullptr)//左为空{root = root->_right;//因为引用所以可以直接改}else if (root->_right == nullptr)//右为空{root = root->_left;}else //左右都不为空{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr)//因为引用,所以下面可以直接new{root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _InsertR(root->_left, key);}else{return false;}}bool _FindR(Node* root, const K& key)//递归版本{if (root == nullptr){return false;}if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return true;}}void _InOrder(Node* root){if (root == NULL){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root;};void Test(){int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTree<int> t;for (auto e : a){t.InsertR(e);}t.InOrder();t.EraseR(4);t.InOrder();t.EraseR(6);t.InOrder();t.EraseR(7);t.InOrder();t.EraseR(3);t.InOrder();for (auto e : a){t.Erase(e);}t.InOrder();}void Test2(){int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BSTree<int> t;for (auto e : a){t.Insert(e);}t.InOrder();BSTree<int> t1(t);t1.InOrder();}
}namespace key_value
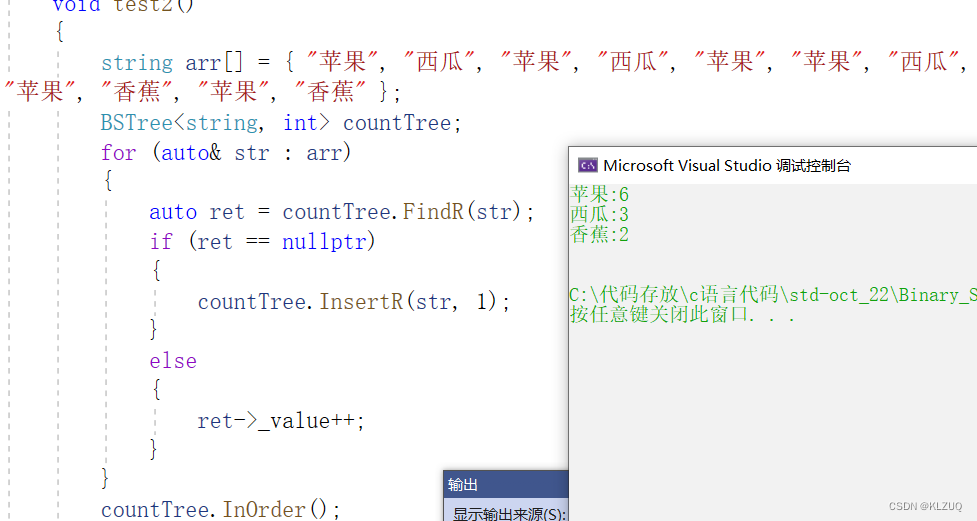
{template<class K, class V >struct BSTreeNode{BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key),_value(value){} };template<class K,class V>class BSTree{typedef BSTreeNode<K,V> Node;public:BSTree():_root(nullptr){}void InOrder(){_InOrder(_root);cout << endl;}Node* FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key, const V& value){return _InsertR(_root, key,value);}bool EraseR(const K& key){return _EraseR(_root, key);}private:bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;if (root->_left == nullptr)//左为空{root = root->_right;//因为引用所以可以直接改}else if (root->_right == nullptr)//右为空{root = root->_left;}else //左右都不为空{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key,const V& value){if (root == nullptr)//因为引用,所以下面可以直接new{root = new Node(key,value);return true;}if (root->_key < key){return _InsertR(root->_right, key,value);}else if (root->_key > key){return _InsertR(root->_left, key,value);}else{return false;}}Node* _FindR(Node* root, const K& key)//递归版本{if (root == nullptr){return nullptr;}if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return root;}}void _InOrder(Node* root){if (root == NULL){return;}_InOrder(root->_left);cout << root->_key << ":"<<root->_value<<endl;_InOrder(root->_right);}private:Node* _root;};void test(){BSTree<string, string> dict;dict.InsertR("insert", "插入");dict.InsertR("right", "右边");dict.InsertR("sort", "排序");dict.InsertR("left", "左边");dict.InsertR("date", "日期");string str;while (cin >> str){BSTreeNode<string, string>* ret = dict.FindR(str);if (ret){cout << ret->_value << endl;}else{cout << "无此单词" << endl;}}}void test2(){string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "香蕉" };BSTree<string, int> countTree;for (auto& str : arr){auto ret = countTree.FindR(str);if (ret == nullptr){countTree.InsertR(str, 1);}else{ret->_value++;}}countTree.InOrder();}
}以上即为本期全部内容,希望大家可以有所收获
如有错误,还请指正
相关文章:

C++二叉树进阶
本期内容我们讲解二叉树的进阶知识,没有看过之前内容的小伙伴建议先看往期内容 二叉树-----补充_KLZUQ的博客-CSDN博客 目录 二叉搜索树 代码实现 基础框架 Insert Find Erase 析构函数 拷贝构造 赋值 二叉搜索树的应用 全部代码 二叉搜索树 二叉搜索树…...

layui tree组件取消勾选
layui(2.8.15) tree的api中,只有 tree.setChecked(id, idArr) 方法,没有取消勾选的方法。 我的需求是:勾选后做判断,如果不符合条件则取消勾选。 实现方法: 使用 tree的oncheck事件,在回调函数中做判断&…...

【Android基础面试题】ViewPager与ViewPager2的区别
ViewPager和ViewPager2是Android中用于实现滑动页面切换的控件。它们的主要区别如下: 实现方式 ViewPager2的内部实现是RecyclerView,而ViewPager是通过继承自ViewGroup实现的。因此,ViewPager2的性能更高。 滑动方向 ViewPager2可以实现横向…...

springCloudGateway网关配置
1.配置跨域支持 /*** 跨域支持*/ Configuration public class CorsConfig {Beanpublic CorsWebFilter corsFilter() {CorsConfiguration config new CorsConfiguration();config.addAllowedMethod("*");config.addAllowedOrigin("*");config.addAllowedH…...

kali 2023.3新增工具
在终端模拟器中运行 sudo apt update && sudo apt full-upgrade 命令来更新其安装 Kali Linux 2023.3 发布中包含了九个新工具,分别是: Calico:云原生网络和网络安全。 cri-tools:用于Kubelet容器运行时接口的命令行界面…...

W25Q64 驱动--基于SPI2接口
前言 (1)本系列是基于STM32的项目笔记,内容涵盖了STM32各种外设的使用,由浅入深。 (2)小编使用的单片机是STM32F105RCT6,项目笔记基于小编的实际项目,但是博客中的内容适用于各种单片…...

禁用无线键盘指定按键
文章目录 前言主体 前言 睡一觉把键盘压坏了一个按键,一开机键盘就自动打出这个字母,我在想用其他按键平替这个字母即可,使用软件修改内部的映射,那么使用autoHotkey软件是十分容易做到的 主体 letter_replace.ahk 创建一个如此命名的文件,然后输入命令即可 a::b 代表平替 a…...
)
分数规划(二分)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 题目描述 小咪是一个土豪手办狂魔,这次他去了一家店,发现了好多好多(n个)手办,但他是一个很怪的人,每次只想买k个手办&a…...
Vue2向Vue3过度Vue3状态管理工具Pinia
目录 1. 什么是Pinia2. 手动添加Pinia到Vue项目3. Pinia基础使用4. getters实现5. action异步实现6. storeToRefs工具函数7. Pinia的调试8. Pinia持久化插件 1. 什么是Pinia Pinia 是 Vue 的专属的最新状态管理库 ,是 Vuex 状态管理工具的替代品 2. 手动添加Pinia到…...
STM32--SPI通信与W25Q64(1)
文章目录 前言SPI通信硬件电路移位过程 SPI时序起始与终止条件交换一个字节 W25Q64硬件电路框图 FLASH操作注意事项软件SPI读写W25Q64 前言 USART串口链接入口 I2C通信链接入口 SPI通信 SPI(Serial Peripheral Interface)是一种高速的、全双工、同步的串…...

版本控制工具Git常见用法
Git 是一个非常强大和灵活的版本控制工具,提供了许多命令和功能来管理代码的版本、分支、合并等。以下是一些 Git 的详细用法: 配置相关命令: 设置用户名和邮箱: git config --global user.name "Your Name" git conf…...

Multisim软件安装包分享(附安装教程)
目录 一、软件简介 二、软件下载 一、软件简介 Multisim软件是一款电路仿真和设计软件,由美国国家仪器公司(National Instruments)开发。它提供了一个交互式的图形界面,使用户能够轻松地构建和仿真电路。以下是Multisim软件的详…...
【android12-linux-5.1】【ST芯片】HAL移植后开机卡死
按照ST的官方readme移植HAL后开机一直卡在android界面,看logcat提示写文件时errorcode:-13。查下资料大致明白13错误码是权限不足,浏览代码在写文件的接口加日志后,发现是需要写iio:device*/buffer/enable这类文件的时候报错的。千…...
线程池也就那么一回事嘛!
线程池详讲 一、线程池的概述二、线程池三、自定义线程池四、线程池工作流程图五、线程池应用场景 一、线程池的概述 线程池其实就是一种多线程处理形式,处理过程中可以将任务添加到队列中,然后在创建线程后自动启动这些任务。这里的线程就是我们前面学过…...
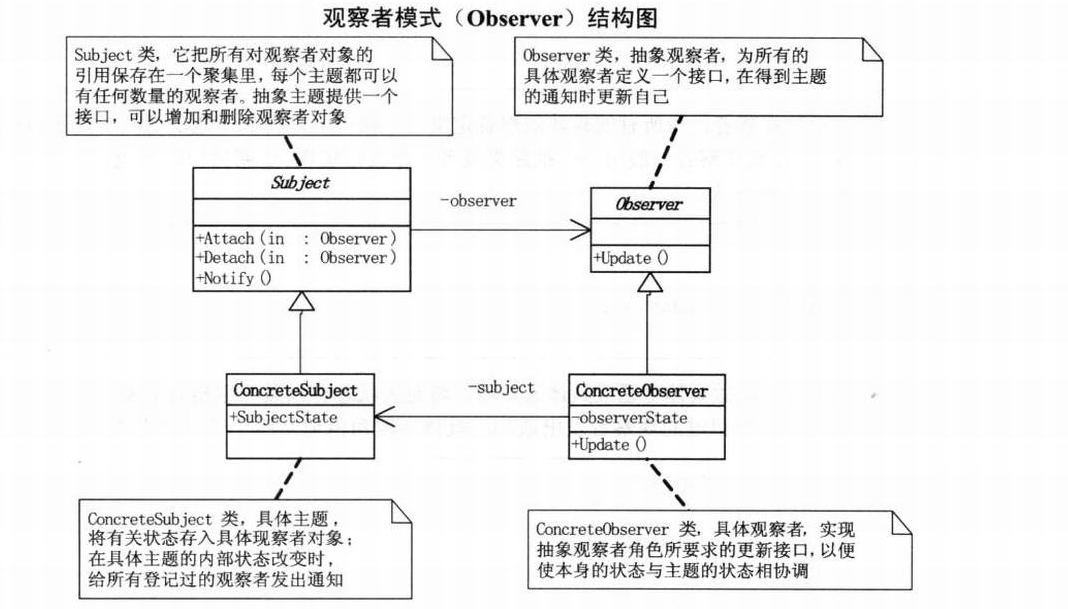
设计模式(11)观察者模式
一、概述: 1、定义:观察者模式定义了一种一对多的依赖关系,让多个观察者对象同时监听某一个主题对象。这个主题对象在状态发生变化时,会通知所有观察者对象,使它们能够自动更新自己。 2、结构图: public interface S…...

开源的安全性:挑战与机会
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

wireshark 流量抓包例题重现
[TOC](这里写目录标题 wireshark抓包方法wireshark组成 wireshark例题 wireshark抓包方法 wireshark组成 wireshark的抓包组成为:分组列表、分组详情以及分组字节流。 上面这一栏想要显示,使用:CtrlF 我们先看一下最上侧的搜索栏可以使用的…...
Smartbi电子表格软件版本更新,首次推出Excel轻应用和语音播放
Smartbi电子表格软件又又又更新啦! 此次更新,首次推出了新特性——Excel轻应用和语音播报。另外,还对产品功能、Demo示例、配套文档进行了完善和迭代。 低代码开发Excel轻应用 可实现迅速发布web应用 业务用户的需求往往都处于“解决问题”…...
ElasticSearch简介、安装、使用
一、什么是ElasticSearch? Elasticsearch 是 Elastic Stack 核心的分布式搜索和分析引擎。 Logstash 和 Beats 有助于收集、聚合和丰富您的数据并将其存储在 Elasticsearch 中。 Kibana 使您能够以交互方式探索、可视化和分享对数据的见解,并管理和监…...

Navicat 连接 mysql 问题
需要将mysql配置文件设置为远程任意ip可登陆,注释掉一下两行配置 # bind-address>->--- 127.0.0.1 # mysqlx-bind-address>-- 127.0.0.1Cant connect to MySQL server on "192.168.137.139 (10013 "Unknown error") 检查Navicat是否联网H…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
