【算法系列篇】前缀和

文章目录
- 前言
- 什么是前缀和算法
- 1.【模板】前缀和
- 1.1 题目要求
- 1.2 做题思路
- 1.3 Java代码实现
- 2. 【模板】二维前缀和
- 2.1 题目要求
- 2.2 做题思路
- 2.3 Java代码实现
- 3. 寻找数组的中心下标
- 3.1 题目要求
- 3.2 做题思路
- 3.3 Java代码实现
- 4. 除自身以外的数组的乘积
- 4.1 题目要求
- 4.2 做题思路
- 4.3 Java代码实现
- 5. 和为 k 的子数组
- 5.1 题目要求
- 5.2 做题思路
- 5.3 Java代码实现
- 6.和可被 k 整除的子数组
- 6.1 题目要求
- 6.2 做题思路
- 6.3 Java代码实现
- 7.连续数组
- 7.1 题目要求
- 7.2 做题思路
- 7.3 Java代码实现
- 8.矩阵区域和
- 8.1 题目要求
- 8.3 做题思路
- 8.3 Java代码实现
- 总结
前言
前缀和算法是一种常用的优化技术,用于加速某些涉及连续子数组或子序列求和的问题。它基于一个简单但强大的思想,通过提前计算并存储数组的前缀和,以便在后续查询中可以快速获取任意区间的和。
在许多算法问题中,我们需要频繁地查询子数组的和,例如最大子数组和、连续子数组的平均值等。传统的方法是在每次查询时遍历数组,并计算所需区间的和,这样会导致时间复杂度较高。
而前缀和算法通过预处理数组,计算出每个位置的前缀和,并将其保存在一个额外的数组中。这样,在查询时,我们只需要简单地减去两个前缀和即可得到所需子数组的和,从而将查询时间降低为O(1)的常数复杂度。
什么是前缀和算法
前缀和算法(Prefix Sum Algorithm)是一种用于高效计算数组前缀和的算法。前缀和是指数组中某个位置之前(包括该位置)所有元素的和。
前缀和算法的基本思想是通过一次遍历数组,计算每个位置的前缀和,并将其存储在一个新的数组中。然后,可以通过查询新数组中的元素,快速计算出任意子数组的和。
具体步骤如下:
- 创建一个新的数组prefixSum,长度与原数组相同。
- 初始化prefixSum[0]为原数组的第一个元素。
- 从原数组的第二个元素开始,依次计算prefixSum[i] = prefixSum[i-1] + nums[i],其中nums为原数组。
- 完成后,prefixSum数组中的每个元素即为对应位置之前所有元素的和。
通过前缀和算法,可以在O(1)的时间复杂度内计算出任意子数组的和。例如,要计算原数组中从位置i到位置j的子数组和,只需计算prefixSum[j] - prefixSum[i-1]即可。如果i为0,则直接返回prefixSum[j]。
前缀和算法在解决一些与子数组和相关的问题时非常有用,例如求解子数组和等于目标值的个数、求解最大子数组和、求解最长连续子数组和等。
1.【模板】前缀和
https://www.nowcoder.com/practice/acead2f4c28c401889915da98ecdc6bf?tpId=230&tqId=2021480&ru=/exam/oj&qru=/ta/dynamic-programming/question-ranking&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595%25E7%25AF%2587%26topicId%3D196
1.1 题目要求
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextInt()) { // 注意 while 处理多个 caseint a = in.nextInt();int b = in.nextInt();System.out.println(a + b);}}
}
1.2 做题思路
按照暴力解法的思路,每次查询 l 到 r 之间的和的时候,就需要遍历一次数组,那么这样的时间复杂度就是 O(q*n) 了,因为进行了较多的重复计算,导致时间效率较低,那么是否有一种方法可以减少重复计算呢?答案是有的,这就是前缀和的思路,其实有点类似于前面我为大家分享的滑动窗口中进窗口的操作,每次进窗口更新数据的时候只需要用前面已经计算了的数字的和加上进窗口的那个数据,就得到了当前位置之前所有元素的和。通过这样的思路就大大减少了重复计算。
然后这个求 l 到 r 之间元素的和的时候,就只需要用 r 和 r 之前所有元素的和减去 l 之前所有元素的和就可以了。
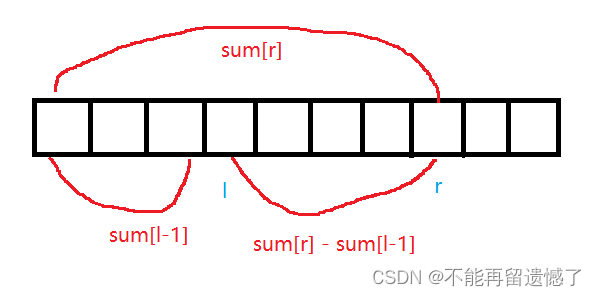
并且仔细的人可能会发现:为什么 l 和 r 都是从1开始而不是0呢?因为从下标为0开始的话,就需要求0 ~ -1 之间元素的和,但是这个区间是不合法的,所以数组从 1 开始就可以防止出现这种的情况。
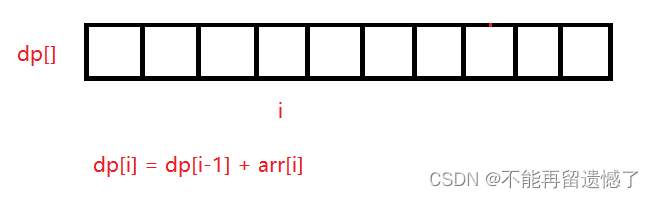
在开始求 l 到 r 之间元素的和的时候,可以先对数组进行一个预处理,求出数组中每个位置之前的前缀和。
1.3 Java代码实现
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextInt()) { // 注意 while 处理多个 caseint n = in.nextInt(),q = in.nextInt();int[] arr = new int[n + 1];for(int i = 1; i <= n; i++) arr[i] = in.nextInt();//创建一个同样大小的前缀和数组,并且因为是多个元素的和,//可能会超出int所能表示的最大范围,这里用long来表示long[] dp = new long[n + 1]; for(int i = 1; i <= n; i++) {dp[i] = dp[i-1] + arr[i];}for(int i = 0; i < q; i++) {int l = in.nextInt(),r = in.nextInt();System.out.println(dp[r] - dp[l-1]);}} }
}
2. 【模板】二维前缀和
https://www.nowcoder.com/practice/99eb8040d116414ea3296467ce81cbbc?tpId=230&tqId=2023819&ru=/exam/oj&qru=/ta/dynamic-programming/question-ranking&sourceUrl=%2Fexam%2Foj%3Fpage%3D1%26tab%3D%25E7%25AE%2597%25E6%25B3%2595%25E7%25AF%2587%26topicId%3D196
2.1 题目要求

import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextInt()) { // 注意 while 处理多个 caseint a = in.nextInt();int b = in.nextInt();System.out.println(a + b);}}
}
2.2 做题思路
二维前缀和和一维前缀和的思路基本上相同的,只是一个是一维数组,一个是二维数组,一些处理细节不同。
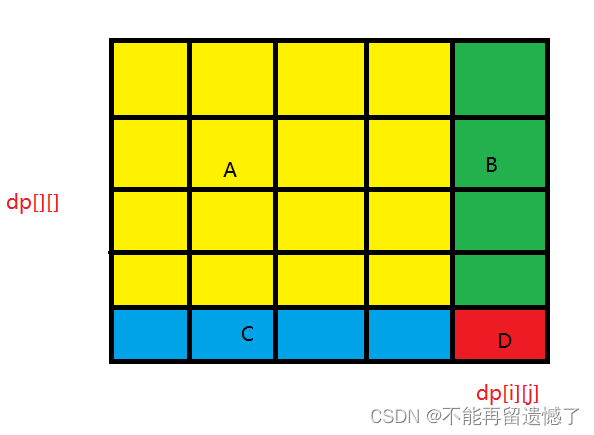
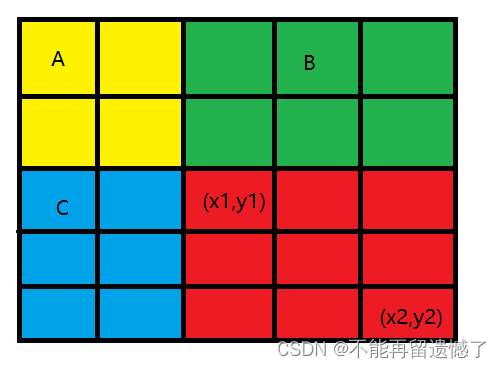
当求 dp[i][j] 的时候,可以将 dp 数组分成 A、B、C、D 四个部分,A 部分是从 0,0 位置开始到 i - 1,j - 1 位置之间的矩阵元素的和。dp[i][j] = A + B + C + D 之间的元素的和,但是这里 B 和 C 区间之间的元素不是很容易求和,所以我们可以用
(A + B) + (A + C) + D - A 来求 dp[i][j] 的值。
然后(x1,y1) 到 (x2,y2)之间的矩阵的和,我们可以使用 dp[x2][y2] - (A + B) - (A + C) + A,也就是 dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]。
2.3 Java代码实现
import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {public static void main(String[] args) {Scanner in = new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextInt()) { // 注意 while 处理多个 caseint n = in.nextInt(),m = in.nextInt(),q = in.nextInt();int[][] arr = new int[n + 1][m + 1];for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {arr[i][j] = in.nextInt();}}//构造二维前缀和数组long[][] dp = new long[n + 1][m + 1];for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + arr[i][j] - dp[i - 1][j - 1];}}for(int i = 0; i < q; i++) {int x1 = in.nextInt(),y1 = in.nextInt(),x2 = in.nextInt(),y2 = in.nextInt();System.out.println(dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1 - 1][y1 - 1]);}}}
}

3. 寻找数组的中心下标
https://leetcode.cn/problems/find-pivot-index/description/
3.1 题目要求
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
输入:nums = [1, 7, 3, 6, 5, 6]
输出:3
解释:
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
输入:nums = [1, 2, 3]
输出:-1
解释:
数组中不存在满足此条件的中心下标。
示例 3:
输入:nums = [2, 1, -1]
输出:0
解释:
中心下标是 0 。
左侧数之和 sum = 0 ,(下标 0 左侧不存在元素),
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
提示:
- 1 <= nums.length <= 104
- -1000 <= nums[i] <= 1000
class Solution {public int pivotIndex(int[] nums) {}
}
3.2 做题思路
这个题目要求我们找到一个元素,这个元素的左边所有元素的和等于该元素右边所有元素的和,通过前面的两个题目我们做这道题目应该是会有一点思路的。
因为要求的是某一元素左边部分和前面部分的元素的和,所以我们可以使用两个数组,分别记录数组中每一个元素的前缀和以及后缀和,前缀和数组从前往后插入数据,后缀和数组从后往前插入数据,并且前缀和的第一个数据为0,后缀和的最后一个数据为0。最后再遍历一次数组,判断数组某一位置的前缀和是否等于后缀和。
3.3 Java代码实现
class Solution {public int pivotIndex(int[] nums) {int n = nums.length;int[] f = new int[n]; //前缀和数组int[] g = new int[n]; //后缀和数组for(int i = 1; i < n; i++) {f[i] = f[i-1] + nums[i - 1];}for(int i = n - 2; i >= 0; i--) {g[i] = g[i + 1] + nums[i + 1];}for(int i = 0; i < n; i++) {if(f[i] == g[i]) return i;}return -1;}
}
4. 除自身以外的数组的乘积
https://leetcode.cn/problems/product-of-array-except-self/
4.1 题目要求
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
- 2 <= nums.length <= 105
- -30 <= nums[i] <= 30
- 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
class Solution {public int[] productExceptSelf(int[] nums) {}
}
4.2 做题思路
这个题目跟上面的 寻找数组的中心下标 思路基本上差不多,只是判断前缀和和后缀和相等的操作换成了前缀积和后缀积的乘积,这里我就不过多介绍了,大家可以直接看代码。
4.3 Java代码实现
class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] f = new int[n];int[] g = new int[n];//这里需要注意前缀积的第一个元素和后缀积的最后一个元素要初始化为1,因为是乘法f[0] = 1;g[n-1] = 1;for(int i = 1; i < n; i++) {f[i] = f[i - 1] * nums[i - 1];}for(int i = n-2; i >= 0; i--) {g[i] = g[i + 1] * nums[i + 1];}int[] ret = new int[n];for(int i = 0; i < n; i++) {ret[i] = f[i] * g[i];}return ret;}
}
5. 和为 k 的子数组
https://leetcode.cn/problems/subarray-sum-equals-k/description/
5.1 题目要求
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。
示例 1:
输入:nums = [1,1,1], k = 2
输出:2
示例 2:
输入:nums = [1,2,3], k = 3
输出:2
提示:
- 1 <= nums.length <= 2 * 104
- -1000 <= nums[i] <= 1000
- -107 <= k <= 107
class Solution {public int subarraySum(int[] nums, int k) {}
}
5.2 做题思路
还是先来看看暴力解法是怎样解决的?遍历数组,以数组的每一元素为起始位置,然后看以该元素为起始位置的子数组是否和为 k ,暴力解法的时间复杂度为 O(N*2)。
很多人看到这个题目首先想到的可能是 滑动窗口 ,但是我们需要仔细看题目,使用滑动窗口,需要保证窗口具有单调性,这里题目没有说数组全为非负数或者非整数,所以不能保证窗口的单调性,不能使用滑动窗口。
换个思路,它既然求的是和为 k 的子数组,我们仍然可以使用前缀和的思想,在数组的某个位置之前找到 该位置的前缀和 - k = 该位置之前的某一位置的前缀和,并且这个题目求的是 子数组的个数,我们可以配合着哈希表来进行计数。哈希表中存储的是某一位置的前缀和以及该前缀和出现的次数。
与暴力解法的思路有些许的区别,在构建前缀和数组的时候,我们不以数组中每个元素作为起始位置,而是将每个元素作为结束位置,这样更贴合我们的前缀和思想。

5.3 Java代码实现
class Solution {public int subarraySum(int[] nums, int k) {Map<Integer,Integer> map = new HashMap<>();//为了防止从0开始到某一位置的子数组的和为k,所以提前放入一个前缀和为0的键值对map.put(0,1); int n = nums.length;int ret = 0,sum = 0;for(int i = 0; i < n; i++) {sum += nums[i];ret += map.getOrDefault(sum-k,0);map.put(sum,map.getOrDefault(sum,0) + 1);}return ret;}
}
6.和可被 k 整除的子数组
https://leetcode.cn/problems/subarray-sums-divisible-by-k/description/
6.1 题目要求
给定一个整数数组 nums 和一个整数 k ,返回其中元素之和可被 k 整除的(连续、非空) 子数组 的数目。
子数组 是数组的 连续 部分。
示例 1:
输入:nums = [4,5,0,-2,-3,1], k = 5
输出:7
解释:
有 7 个子数组满足其元素之和可被 k = 5 整除:
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]
示例 2:
输入: nums = [5], k = 9
输出: 0
提示:
- 1 <= nums.length <= 3 * 104
- -104 <= nums[i] <= 104
- 2 <= k <= 104
class Solution {public int subarraysDivByK(int[] nums, int k) {}
}
6.2 做题思路
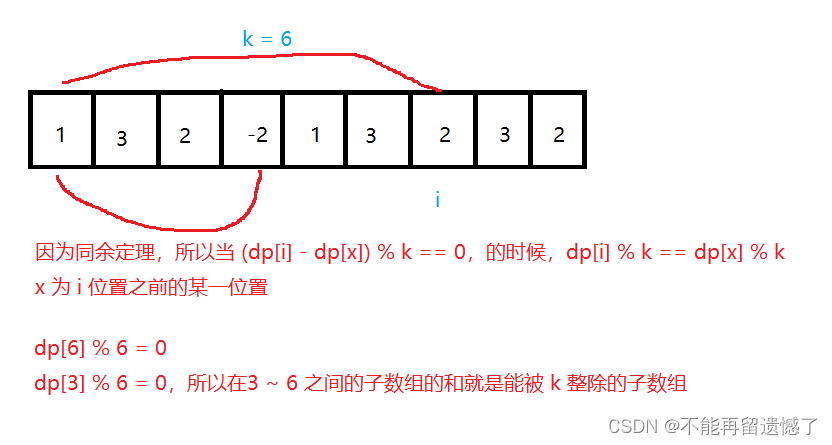
在做这个题目之前,我们需要知道两个额外的知识点:
- 同余定理
- 如果 (a - b) % n == 0 ,那么我们可以得到⼀个结论: a % n == b % n 。⽤⽂字叙述就是,如果两个数相减的差能被n整除,那么这两个数对n取模的结果相同。

- 在c++和Java中对负数取模的话,结果会是一个负数,所以需要修正负数取模的结果 (a % n + n) % n(a为负数)
当知道这两个定理之后,那么这个题目的思路就跟上面的 和为 k 的子数组 思路是类似的。
6.3 Java代码实现
class Solution {public int subarraysDivByK(int[] nums, int k) {Map<Integer,Integer> map = new HashMap<>();//同样为了防止从0开始到某一位置的子数组的乘积都能被k整除map.put(0 % k,1);int n = nums.length;int sum = 0,ret = 0;for(int i = 0; i < n; i++) {sum += nums[i];int r = (sum % k + k) % k;ret += map.getOrDefault(r,0);map.put(r,map.getOrDefault(r,0) + 1);}return ret;}
}
7.连续数组
https://leetcode.cn/problems/contiguous-array/description/
7.1 题目要求
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
示例 1:
输入: nums = [0,1]
输出: 2
说明: [0, 1] 是具有相同数量 0 和 1 的最长连续子数组。
示例 2:
输入: nums = [0,1,0]
输出: 2
说明: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。
提示:
- 1 <= nums.length <= 105
- nums[i] 不是 0 就是 1
class Solution {public int findMaxLength(int[] nums) {}
}
7.2 做题思路
因为数组中只有二进制数,也就是0和1,我们可以将0当成是-1,当子数组中0和1的数量相同的时候,子数组的和为0。所以这个题目也就相当于求长度最长的和为0的子数组。所以我们哈希表中存储的就是前缀和以及数组的下标。
7.3 Java代码实现
class Solution {public int findMaxLength(int[] nums) {Map<Integer,Integer> map = new HashMap<>();map.put(0,-1);int n = nums.length;int ret = 0,sum = 0;for(int i = 0; i < n; i++) {sum += (nums[i] == 0 ? -1 : 1);if(map.containsKey(sum)) ret = Math.max(ret,i-map.getOrDefault(sum,0));else map.put(sum,i);}return ret;}
}
8.矩阵区域和
https://leetcode.cn/problems/matrix-block-sum/description/
8.1 题目要求
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
- i - k <= r <= i + k,
- j - k <= c <= j + k 且
- (r, c) 在矩阵内。
示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]
示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出:[[45,45,45],[45,45,45],[45,45,45]]
提示:
- m == mat.length
- n == mat[i].length
- 1 <= m, n, k <= 100
- 1 <= mat[i][j] <= 100
class Solution {public int[][] matrixBlockSum(int[][] mat, int k) {}
}
8.3 做题思路
这个题目跟上面的【模板】二维前缀和是类似的,只是这个题目需要我们找到对应的矩阵。
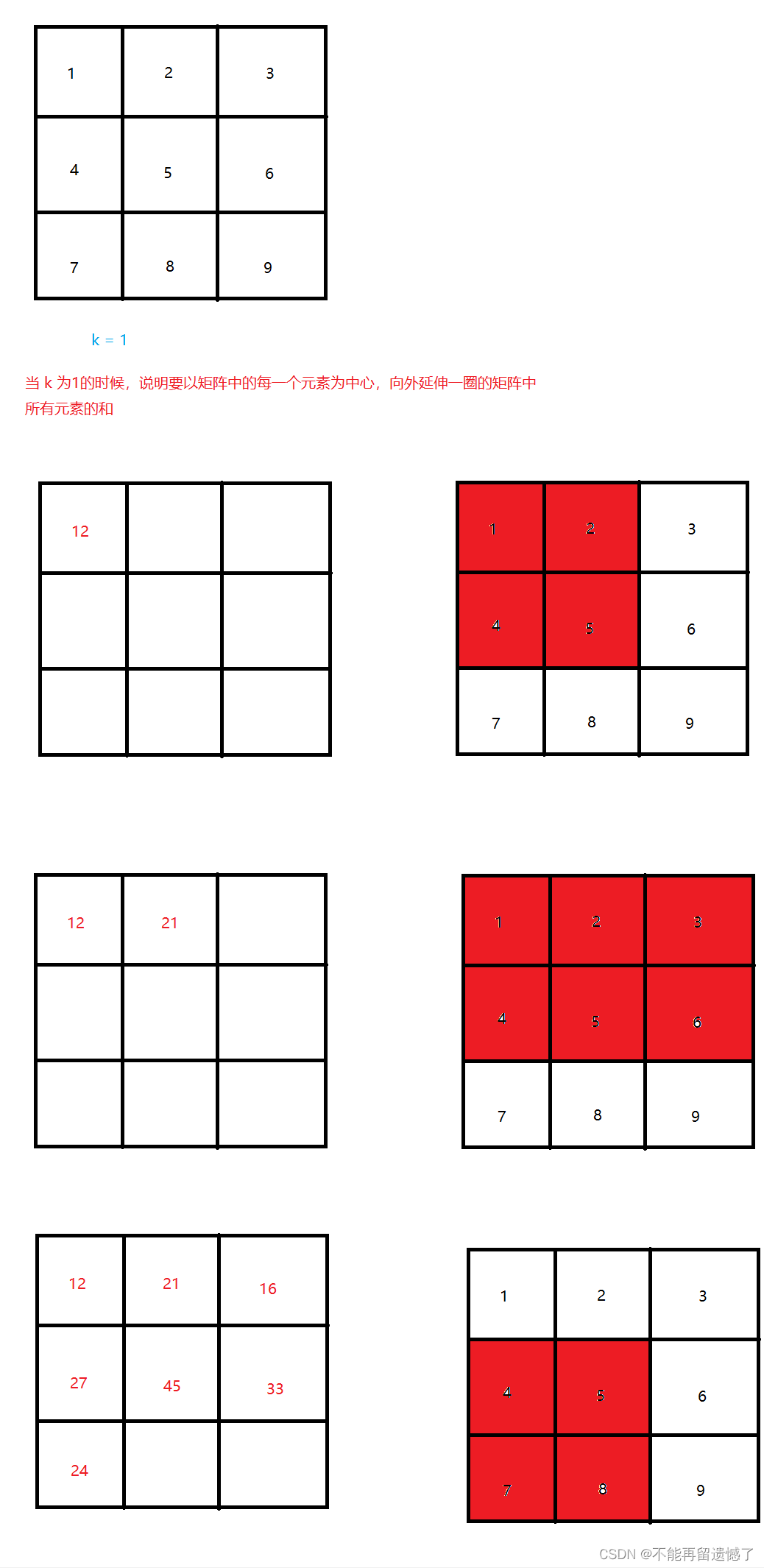
需要注意的是,题目中的 r 和 c 都是从0开始的,也就是说,可能会出现数组越界的情况,这道题题目的重点就是需要处理下标越界的情况。那么如何处理下标越界的情况呢?很简单,前面的不是有从下标1开始的吗?当我们构建前缀和数组的时候,我们也可以将数组下标以1开始,然后在最终结果的数组中填入数据的时候注意下标的映射关系就行了。
8.3 Java代码实现
class Solution {public int[][] matrixBlockSum(int[][] mat, int k) {int n = mat.length;int m = mat[0].length;int[][] dp = new int[n + 1][m + 1];for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + mat[i - 1][j - 1] - dp[i - 1][j - 1];}}int[][] ret = new int[n][m];for(int i = 0; i < n; i++) {for(int j = 0; j < m; j++) {//处理下标越界问题,并且解决了下标的映射关系int x1 = Math.max(0,i-k) + 1,y1 = Math.max(0,j - k) + 1;int x2 = Math.min(n - 1,i + k) + 1,y2 = Math.min(m - 1,j + k) + 1;ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];}}return ret;}
}
总结
通过前缀和算法,我们可以在O(1)的时间复杂度内计算出任意区间的元素和。这在处理大规模数据时非常有用,可以大大提高计算效率。
总结起来,前缀和算法是一种高效计算数组区间和的方法。它通过计算数组的前缀和,可以在O(1)的时间复杂度内得到任意区间的元素和。在实际应用中,前缀和算法经常用于解决数组区间和相关的问题,例如子数组的最大和、子数组的平均值等。通过掌握前缀和算法,我们可以更加高效地解决这类问题。
相关文章:

【算法系列篇】前缀和
文章目录 前言什么是前缀和算法1.【模板】前缀和1.1 题目要求1.2 做题思路1.3 Java代码实现 2. 【模板】二维前缀和2.1 题目要求2.2 做题思路2.3 Java代码实现 3. 寻找数组的中心下标3.1 题目要求3.2 做题思路3.3 Java代码实现 4. 除自身以外的数组的乘积4.1 题目要求4.2 做题思…...
若依移动端Ruoyi-App 项目的后端项目入门
后端项目运行 运行报错 Error creating bean with name sysConfigServiceImpl: Invocation of init method failed 数据库创建了。 代码连接数据库地方了也匹配上了。但是还是报错。 分析 : 想起来我电脑从来没有安装过redis 下载安装redis到windows 链接&…...

(学习笔记-调度算法)内存页面置换算法
在了解内存页面置换算法前,我们得先了解 缺页异常(缺页中断)。 当 CPU 访问的页面不在物理内存中时,便会产生一个缺页中断,请求操作系统将缺页调入到物理内存。那它与一般的中断主要区别在于: 缺页中断在指令执行 [期…...

行为型模式-观察者模式
1.观察者设计模式* 定义:当对象间存在一对多关系时,则使用观察者模式(Observer Pattern)。比如,当一个对象被修改时,则会自动通知依赖它的对象。观察者模式属于行为型模式。 意图:定义对象间的…...

前端面试:【新技术与趋势】WebAssembly、Serverless、GraphQL
在不断演进的技术领域中,WebAssembly、Serverless和GraphQL都是备受关注的新技术和趋势。它们改变了软件开发、部署和数据传输的方式,为开发者提供了更多的选择和灵活性。 1. WebAssembly(Wasm): 简介: Web…...
【ubuntu】 20.04 网络连接器图标不显示、有线未托管、设置界面中没有“网络”选项等问题解决方案
问题 在工作中 Ubuntu 20.04 桌面版因挂机或不当操作,意外导致如下问题 1、 Ubuntu 网络连接图标消失 2、 有线未托管 上图中展示的是 有线 已连接 ,故障的显示 有限 未托管 或其他字符 3、 ”设置“ 中缺少”网络“选项 上图是设置界面,…...
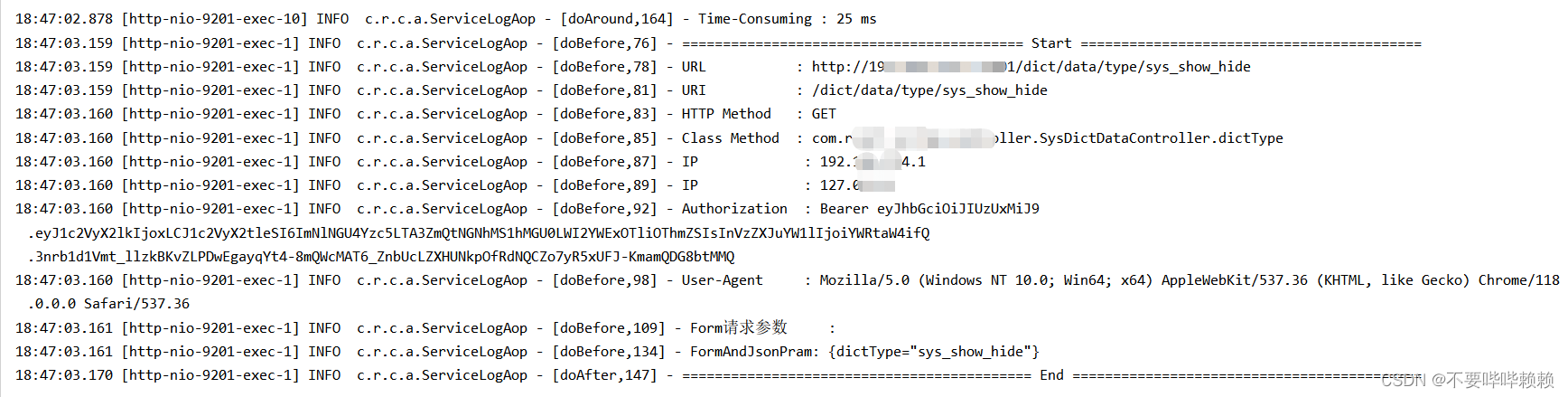
SpringCloud/SpringBoot多模块项目中配置公共AOP模块实现打印子模块Controller所有请求参数与日志
项目中遇到多个模块需要打印Controller请求日志,在每个模块里面加AOP并且配置单独的切面笔者认为代码冗余,于是乎就打算把AOP日志打印抽离成一个公共模块,谁想用就引入Maven坐标就行。 定义公共AOP模块 并编写AOP工具 AOP模块pom.xml如下 &…...

【GeoDa实用技巧100例】022:geoda生成空间权重矩阵(邻接矩阵、距离矩阵)
geoda生成空间权重矩阵(邻接矩阵、距离矩阵),车式矩阵、后式矩阵、K邻接矩阵。 文章目录 一、概述二、“车式”邻接的gal文档生成三、“后式”邻接gal文档生成四、k最近邻居gat文档生成五、查看gal和gat文档一、概述 空间权重矩阵(或相应的表格形式)一般需要用计算机软件生…...
基于web的鲜花商城系统java jsp网上购物超市mysql源代码
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 基于web的鲜花商城系统 系统有2权限:前台…...
意外发现Cortex-M内核带的64bit时间戳,比32bit的DWT时钟周期计数器更方便,再也不用担心溢出问题了
视频: https://www.bilibili.com/video/BV1Bw411D7F5 意外发现Cortex-M内核带的64bit时间戳,比32bit的DWT时钟周期计数器更方便,再也不用担心溢出问题了 介绍: 看参数手册的Debug章节,System ROM Table里面带Timestam…...
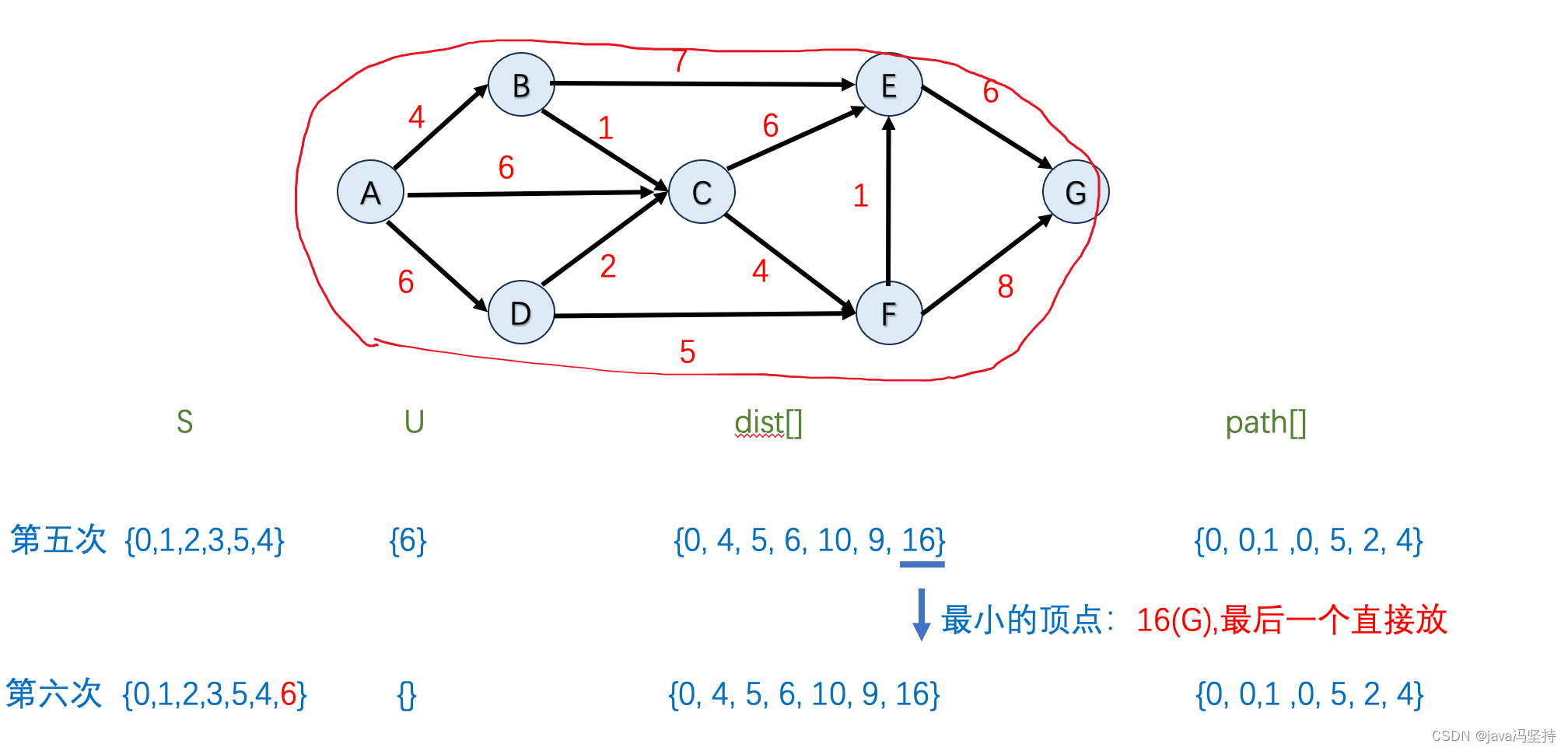
数据结构与算法细节篇之最短路径问题:Dijkstra和Floyd算法详细描述,java语言实现。
文章目录 前言一、单源最短路径1、单源最短路径问题2、Dijkstra 初始化a、参数b、初始化参数c、算法步骤 3、Dijkstra 算法详细步骤a、第一轮算法执行b、第二轮算法执行c、第三轮算法执行d、第四轮算法执行e、第五轮算法执行f、第六轮算法执行 4、java算法实现 二、多源最短路径…...
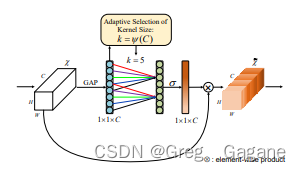
改进YOLO系列:6.添加ECA注意力机制
添加ECA注意力机制 1. ECA注意力机制论文2. ECA注意力机制原理3. ECA注意力机制的配置3.1common.py配置3.2yolo.py配置3.3yaml文件配置1. ECA注意力机制论文 论文题目:ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks 论文链接:ECA-N…...
软件测试知识点总结(一)
文章目录 前言一. 什么是软件测试二. 软件测试和软件调试的区别三. 软件测试和研发的区别四. 优秀的测试人员所应该具备的素质总结 前言 在现实生活中的很多场景下,我们都会进行测试。 比如买件衣服,我们需要看衣服是不是穿着好看,衣服材质如…...

持续集成与持续交付:现代软件测试的变革之路
引言 在数字化时代,软件开发的速度和复杂性都在不断增加。为了满足市场的需求,企业需要更快、更高效地交付高质量的软件产品。在这样的背景下,持续集成与持续交付(CI/CD)成为了软件开发和测试的核心实践。 软件开发的…...
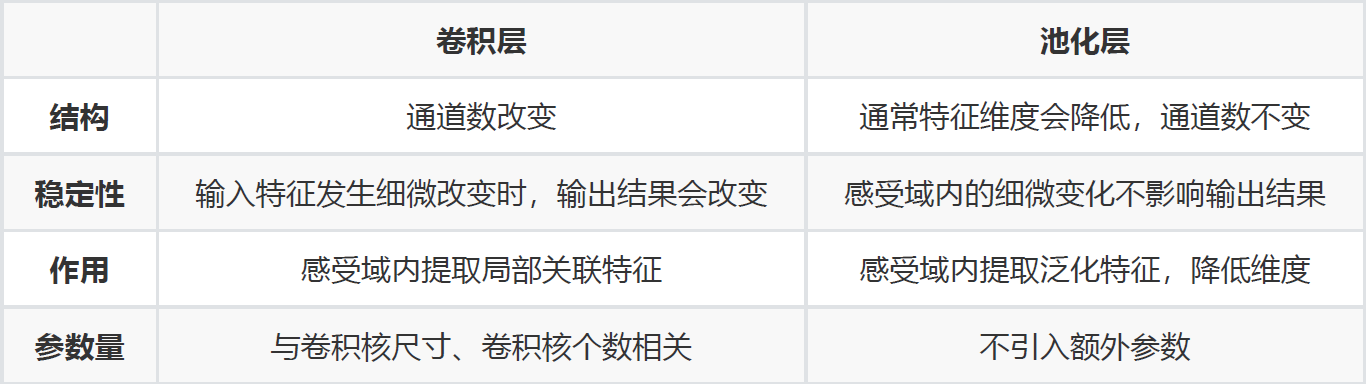
深度学习基本理论下篇:(梯度下降/卷积/池化/归一化/AlexNet/归一化/Dropout/卷积核)、深度学习面试
深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播) 深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播)、深度学习面试_会害羞的杨…...
)
[Ubuntu 20.04] 通过udev规则修改网卡名称(例如eth0)
在 Ubuntu 20.04 操作系统中,默认情况下,网卡接口名称采用了一种较为复杂的命名方式(如 enp0s3、eth0 等)。然而,有时候我们可能更希望使用更简洁和易于识别的名称来标识不同的网络接口。那么如何在 Ubuntu 20.04 中修改网卡接口的名称,以满足个性化需求。 步骤一:查看当…...

Java“牵手”根据关键词搜索(分类搜索)lazada商品列表页面数据获取方法,lazadaAPI实现批量商品数据抓取示例
lazada商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取lazada商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问lazada商城的网页来获取商品详情信息。以下是两种常用方法的介…...
Java—实现多线程程序 | 入门
目录 一、前言 二、基本概念 进程 线程 三、Java多线程实现 java.lang.Thread类 获取线程名字及对象 获取main进程名 Thread currentThread() 四、线程优先级 设置优先级 一、前言 前期入门学习的代码中,全部都是单线的程序,也就是从头到尾…...

8.5 【C语言】指向函数的指针
8.5.1 什么是函数的指针 每次调用函数时都从该地址入口开始执行此段函数代码。函数名代表函数的起始地址。 8.5.2 用函数指针变量调用函数 例8.22 用函数求整数a和b中的大者 解题思路:在主函数调用max函数,除了可以通过函数名调用外,还可…...

C++实现字符串的逆置
目录 C和C的区别 【1】C对C的扩充 【2】C对C的兼容 第一个C程序 【1】hello world 【2】cout标准输出流对象 i)介绍 ii)运算 iii)cout的使用 iv)使用cout指定格式的输出 练习:1、输出斐波那契的前10项。 【3】…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
