8.5 【C语言】指向函数的指针
8.5.1 什么是函数的指针
每次调用函数时都从该地址入口开始执行此段函数代码。函数名代表函数的起始地址。
8.5.2 用函数指针变量调用函数
例8.22 用函数求整数a和b中的大者
解题思路:在主函数调用max函数,除了可以通过函数名调用外,还可以通过指向函数的指针变量来实现。
#include<stdio.h>
int main(){int max(int,int); //函数声明int a,b,c;printf("please enter a and b:");scanf("%d,%d,&a,&b");c=max(a,b); //通过函数名调用max函数printf("a=%d\nb=%d\nmax=%d\n"a,b,c);return 0;
}
int max(int x,int y){int z;if(x>y) z=x;else z=y;return(z);
}(2)通过指针变量调用它所指向的函数
#include<stdio.h>{int main(){int max(int,int); //函数声明int(*p)(int,int); //定义指向函数的指针变量pint a,b,c;p=max;printf("please enter a and b:");scanf("%d,%d",&a,&b);c=(*p)(a,b); //通过指针变量调用max函数printf("a=%d\nb=%d\nmax=%d\n",a,b,c);return 0; }int max(int x,int y){int z;if(x>y) z=x;else z=y;return(z); }
}8.5.3 怎样定义和使用指向函数的指针变量
类型名(*指针变量名)(函数参数表列)
(1)定义指向函数的指针变量,并不意味着这个指针变量可以指向任何函数,它只能指向在定义时指定的类型的函数。
(2)如果要用指针调用函数,必须先使指针变量指向该函数。
(3)在给函数指针变量赋值时,只须给出函数名而不必给出参数。
(4)用函数指针变量调用函数时,只须将(*p)代替函数名即可。
(5)对指向函数的指针变量不能进行算术运算,如p+n,p++,p--等运算是无意义的。
(6)用函数名调用函数,只能调用所指定的一个函数。
8.5.4 用指向函数的指针作函数参数
指向函数的指针变量的一个重要用途是把函数的入口地址作为参数传递到其他函数。
相关文章:

8.5 【C语言】指向函数的指针
8.5.1 什么是函数的指针 每次调用函数时都从该地址入口开始执行此段函数代码。函数名代表函数的起始地址。 8.5.2 用函数指针变量调用函数 例8.22 用函数求整数a和b中的大者 解题思路:在主函数调用max函数,除了可以通过函数名调用外,还可…...

C++实现字符串的逆置
目录 C和C的区别 【1】C对C的扩充 【2】C对C的兼容 第一个C程序 【1】hello world 【2】cout标准输出流对象 i)介绍 ii)运算 iii)cout的使用 iv)使用cout指定格式的输出 练习:1、输出斐波那契的前10项。 【3】…...

论Spring或Spring Boot的花式扩展
文章目录 引言扩展点讲述花式扩展之自动配置类花式扩展之实现接口实现方式样例 花式扩展之自定义starterImport方式SpringFactories方式 总结鸣谢 引言 Spring Boot是一个高度可定制的框架,旨在帮助开发者快速创建、配置和管理他们的应用程序 扩展点讲述 Spring Bo…...

如何评估分类模型的好坏
如何评估分类模型的好坏 评估分类预测模型的质量,常用一个矩阵、三条曲线和六个指标。 一个矩阵:混淆矩阵;三条曲线:ROC曲线、PR曲线、KS曲线;六个指标:正确率Acc、查全率R、查准率P、F值、AUC、BEP值、KS…...

● 84.柱状图中最大的矩形
84.柱状图中最大的矩形 class Solution { public:int largestRectangleArea(vector<int>& heights) {stack<int>st;heights.insert(heights.begin(),0);heights.push_back(0);st.push(0);int res0;for(int i1;i<heights.size();i){while(heights[i]<heig…...

未检查的转换: ‘java.lang.Object‘ 转换为 ‘java.util.List
fastjson方式 Object object ... // 获取待转换的objectList<WbsCategory> list JSON.parseObject(JSON.toJSONString(object), new TypeReference<List<WbsCategory>>() {}); 在这个示例中,我们使用JSON.toJSONString()将object对象转换…...
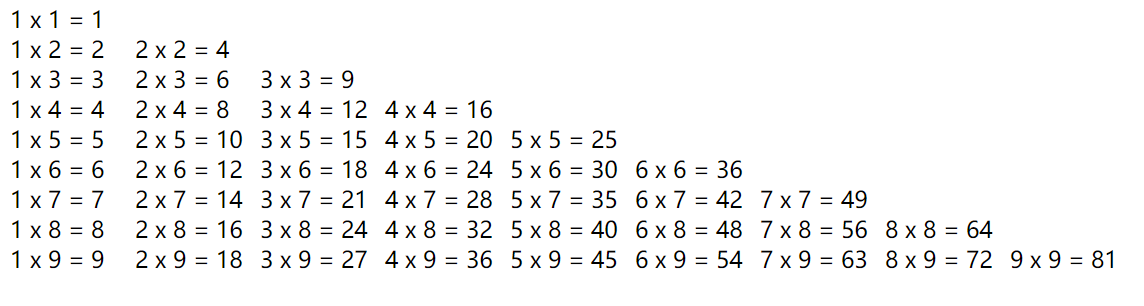
【C语言】使用C语言,实现九九乘法表(另附Python、Java、JavaScript实现方式)
文章目录 1. C语言实现1.1 思路1.2 代码实现 3.其他语言实现3.1 Python实现3.2 Java实现3.3 JavaScript实现 1. C语言实现 1.1 思路 九九乘法表图示: 思路如下:定义两层for循环即可实现九九乘法表 一共有9层,所以要定义一个变量iÿ…...

[机缘参悟-102] :IT人 - 管理的本质?管理人与从事技术的本质区别?人性、冰山模型、需求层次模型
感悟: 管理的本质是:学习各种管理理论、方法、技能,克服自身的人性缺点、预防他人人性的恶点、利用他人的人性特点拿到结果,从而完成组织、管理者的上司、管理者自身、管理者下属的目标。管理中的问题,80%以上都人性问…...
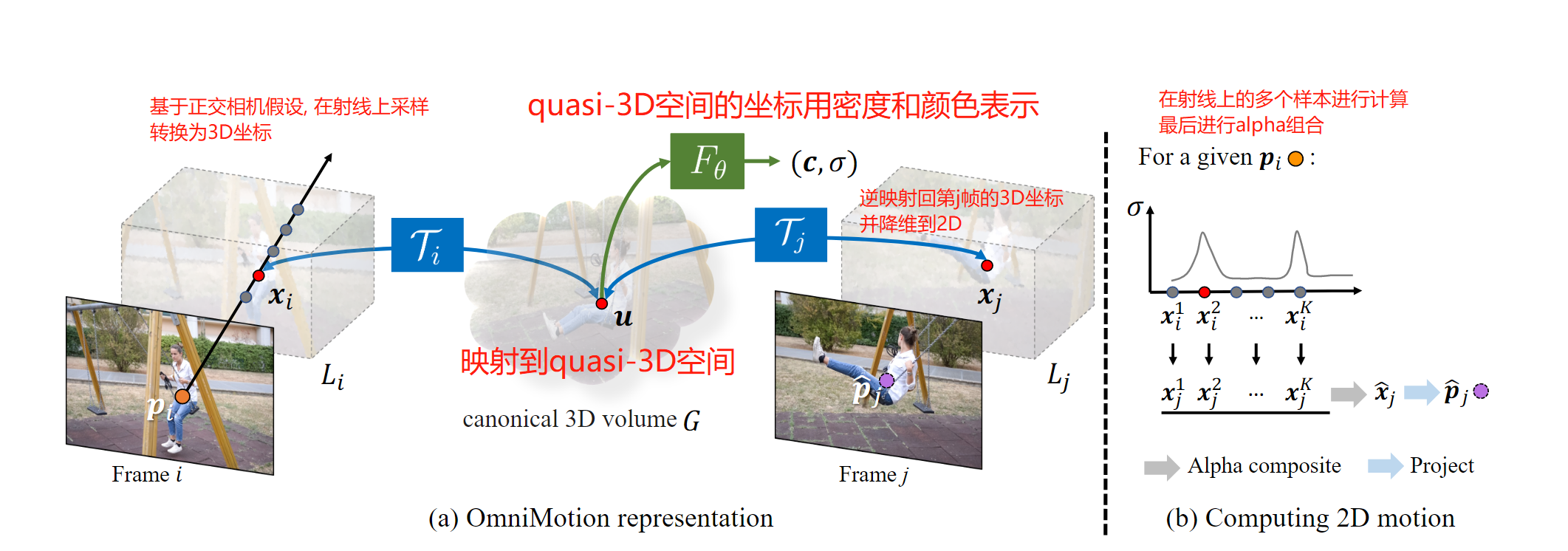
[论文阅读笔记26]Tracking Everything Everywhere All at Once
论文地址: 论文 代码地址: 代码 这是一篇效果极好的像素级跟踪的文章, 发表在ICCV2023, 可以非常好的应对遮挡等情形, 其根本的方法在于将2D点投影到一个伪3D(quasi-3D)空间, 然后再映射回去, 就可以在其他帧中得到稳定跟踪. 这篇文章的方法不是很好理解, 代码也刚开源, 做一…...
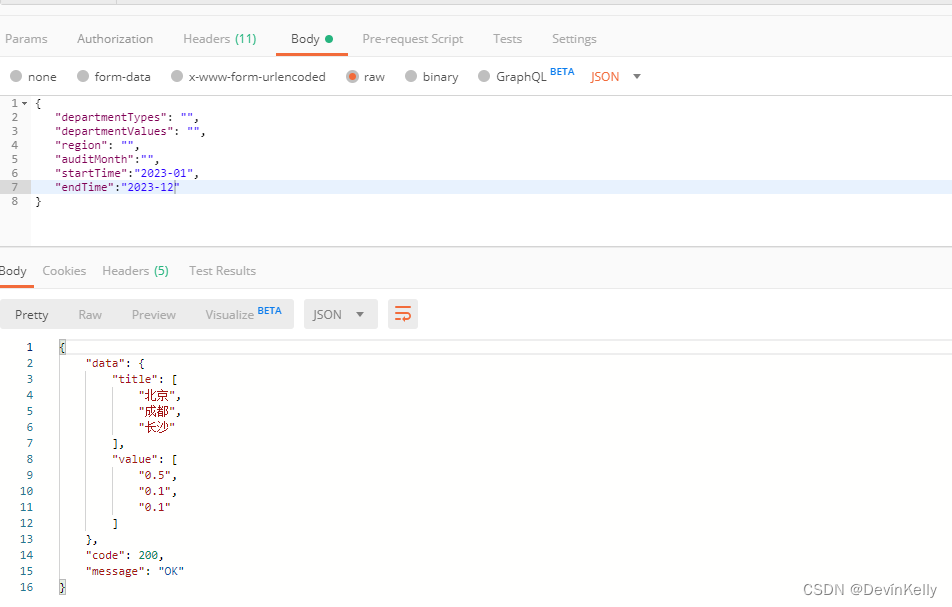
【Java 动态数据统计图】前后端对接数据格式(Map返回数组格式数据)六(120)
说明: 前端使用:vue3.0 前后端对接数据格式:无非就是前端把后端返回的数据处理为自己想要的格式,或者,后端给前端处理好想要的格式; 针对前后端的柱状图,趋势图等数据对接,前端一般需…...
❤ 给自己的mac系统上安装java环境
❤ 给自己的mac系统上安装java环境 🍓 作为前端工程师如何给自己的mac系统上安装java环境 🍎 最近因为自己的一些项目需求,mac电脑上需要安装一些后台的java环境,用来跑后台的java程序,于是从一个前端工程师的角度安…...

Java-匿名类
介绍 匿名类是指没有名字的类,它对一个给定的类进行拓展,或者实现一个给定的接口。使用匿名类可以使得代码更加简洁、紧凑、模块程度更高。 实现方式及语法 匿名类有两种实现方式 继承一个类,重写其方法实现一个接口(可以是多…...
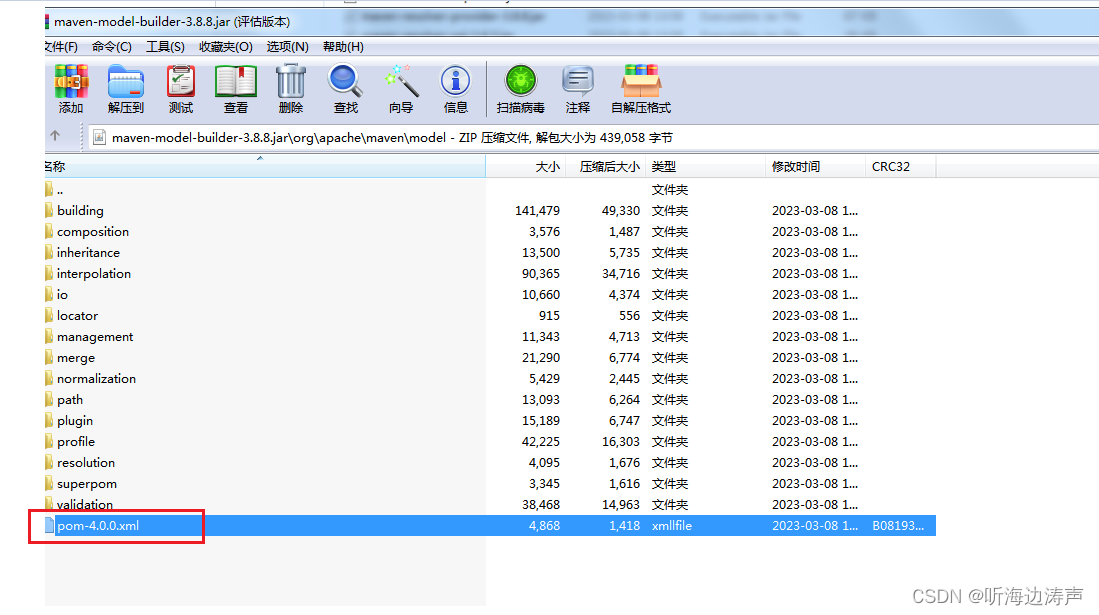
Maven的超级POM
对于我们创建的一个maven工程,即便我们自己的pom.xm文件中没有明确指定一个父工程(父POM),其实也默认继承了超级POM,就好比JAVA类继承Object类一样。 maven官网关于超级POM的介绍: https://maven.apache.o…...

软考高级系统架构设计师系列论文九十二:论新技术的引进
软考高级系统架构设计师系列论文九十二:论新技术的引进 一、摘要二、正文三、总结一、摘要 根据国家税务总局对税务系统内所有系统进行集成与整合的需求,我所在的开发单位组织了全国金税工程防伪税控系统网络版的升级开发工作。该项目工程浩大,要求在具有严格的安全、可靠性…...

vue使用Bootstrap的详细方法
要在Vue中使用Bootstrap,您可以按照以下步骤进行操作: 安装Bootstrap:首先,您需要安装Bootstrap。您可以使用npm或者yarn来安装Bootstrap。打开终端,并在项目的根目录中运行以下命令: npm install bootst…...

leetcode做题笔记103. 二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。 思路一:BFS #define N 2000int** zigzagLevelOrder(st…...
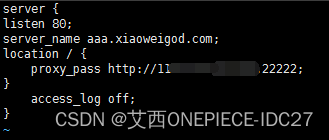
如果将PC电脑变成web服务器:利用Nignx反向代理绕过运营商对80端口封锁
如果将PC电脑变成web服务器:利用Nignx反向代理绕过运营商对80端口封锁 在上一篇文章中,我们已经实现了内网主机的多次端口映射,将内网主机的端口映射到了公网,可以通过公网访问该主机了。 因为电信的家庭宽带,默认是…...

Eureka:服务注册-信息配置-自我保护机制
首先在提供者服务下,添加一个依赖 <!-- Eureka --><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-eureka</artifactId><version>1.4.6.RELEASE</version><…...
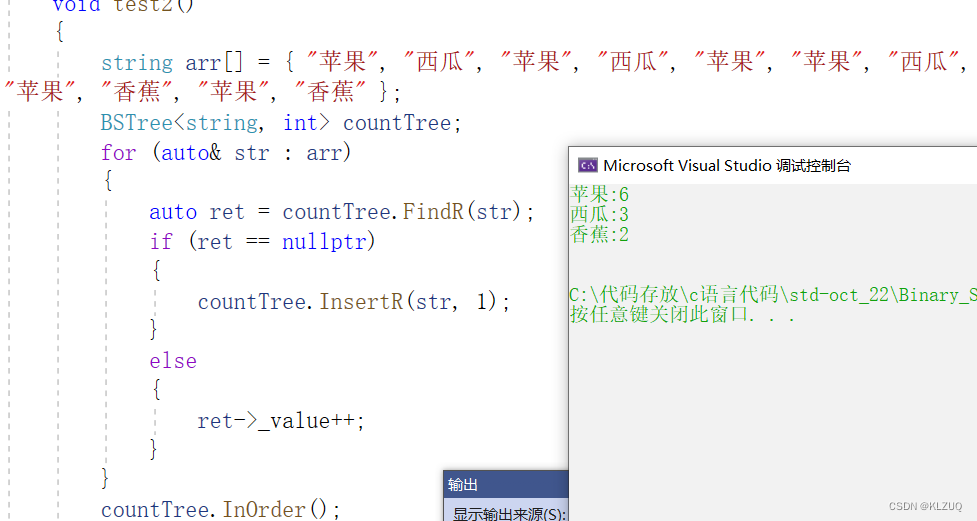
C++二叉树进阶
本期内容我们讲解二叉树的进阶知识,没有看过之前内容的小伙伴建议先看往期内容 二叉树-----补充_KLZUQ的博客-CSDN博客 目录 二叉搜索树 代码实现 基础框架 Insert Find Erase 析构函数 拷贝构造 赋值 二叉搜索树的应用 全部代码 二叉搜索树 二叉搜索树…...

layui tree组件取消勾选
layui(2.8.15) tree的api中,只有 tree.setChecked(id, idArr) 方法,没有取消勾选的方法。 我的需求是:勾选后做判断,如果不符合条件则取消勾选。 实现方法: 使用 tree的oncheck事件,在回调函数中做判断&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
