当前位置： 首页 > news >正文

【C语言】使用C语言，实现九九乘法表（另附Python、Java、JavaScript实现方式）

news 2026/2/9 15:16:10

文章目录

  • 1. C语言实现
    • 1.1 思路
    • 1.2 代码实现
  • 3.其他语言实现
    • 3.1 Python实现
    • 3.2 Java实现
    • 3.3 JavaScript实现

1. C语言实现

1.1 思路

九九乘法表图示：

在这里插入图片描述

思路如下：定义两层for循环即可实现九九乘法表

  • 一共有9层，所以要定义一个变量i，控制九九乘法表表的层数，共循环9次，即i=1;i<=9
  • 第一层有1个数，第二层两个数 … 第九层9个数，也就是说第i层有i个数。
  • 每层数的内容组成有：

    • 乘号x右边的数为当前的层数不变，如第5层右边的数一直是5，因此右边的数就是i

    • 乘号x左边的数从1开始递增到本层的层数，如第5层左边的数依次从1-5，因此一个变量j代表左边的数，循环从1-i，即j=1;j<=i

    • 等于号=后边的数为x左右两边数的乘积，即i*j

    • 最终得到需要打印的内容公式为 j * i = i*j

1.2 代码实现

#include<stdio.h>int main(){	int i,j;for(i=1;i<=9;i++){ // 外层循环，控制乘法表层数，共9层for(j=1;j<=i;j++){ // 内层循环，控制每层共几个数，第i层有i个数printf("%d*%d=%d\t",j,i,i*j);}printf("\n"); // 每层打印结束后换行	}return 0;
}

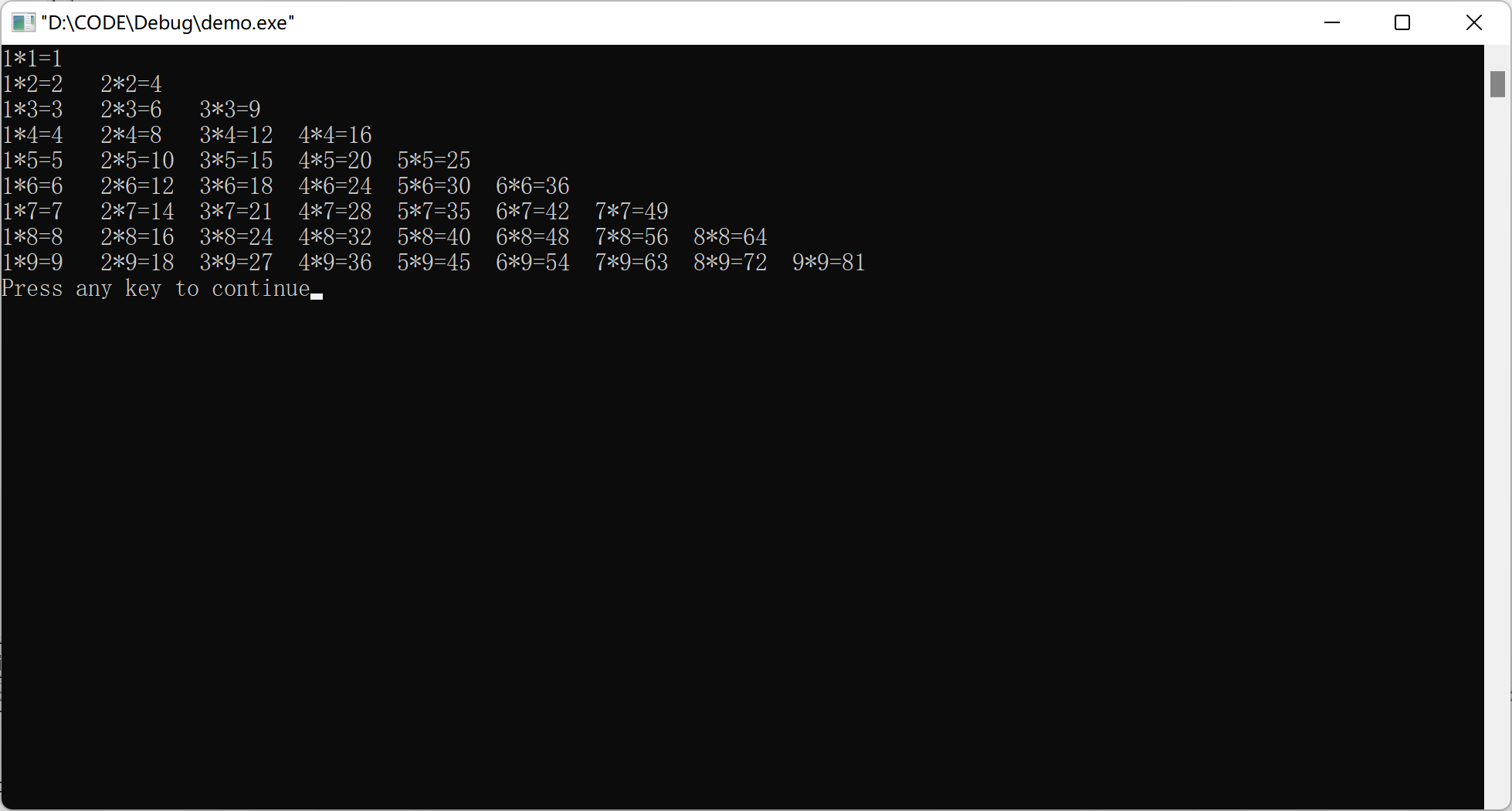
在这里插入图片描述

注：
1.printf("%d*%d=%d\t",j,i,i*j) ，由于九九乘法表中每行的乘号（*）左边的数是从1开始递增的，而右边的数是该行的行数，保持不变，所以打印顺序是j,i,i*j
2.打印时加上\t制表符，使得输出美观
3.每层打印结束后需换行\n

3.其他语言实现

3.1 Python实现

for i in range(1,10):for j in range(1,i+1):print(f'{j} x {i} = {i*j}\t', end='')print('')

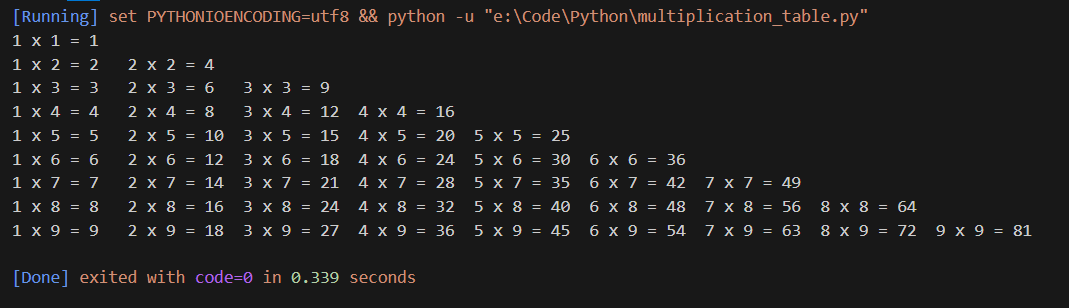
在这里插入图片描述

3.2 Java实现

public class MultiplicationTable {public static void main(String[] args) {for (int i = 1; i <= 9; i++){ // 外层循环，控制乘法表层数，共9层for (int j = 1; j <= i; j++) { // 内层循环，控制每层共几个数，第i层有i个数System.out.print(j + "*" + i + "=" + (j * i) + "\t");}System.out.println(); // 每层打印结束后换行}}
}

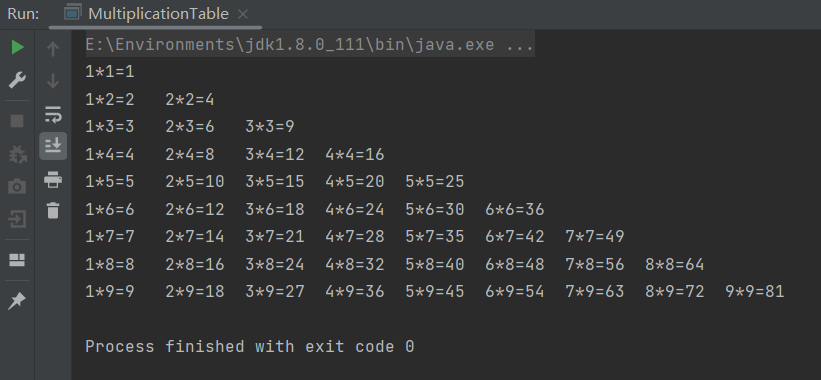
在这里插入图片描述

3.3 JavaScript实现

<!DOCTYPE html>
<html lang="en"><head><meta charset="UTF-8" /><title>九九乘法表</title><style>/* 设置div元素样式 */div {width: 100px;display: inline-block;font-size: 18px;}</style></head><body><script>for (let i = 1; i <= 9; i++) {for (let j = 1; j <= i; j++) {document.write(`<div>${j} x ${i} = ${i * j}</div>`); // 写入div元素至页面}document.write("<br/>"); // 换行}</script></body>
</html>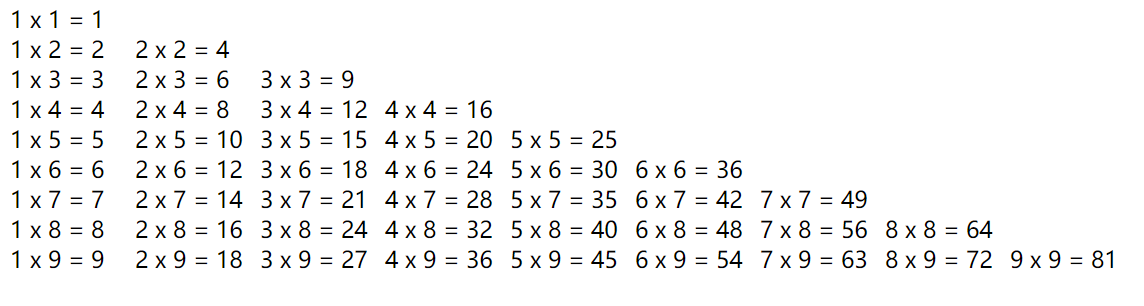

在这里插入图片描述

相关文章：

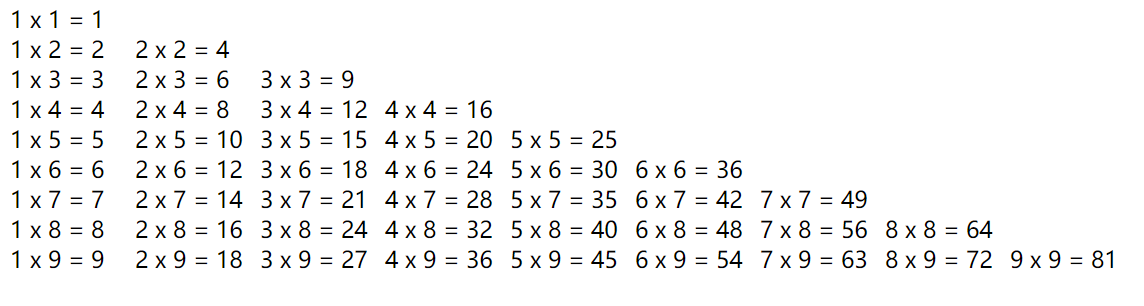
【C语言】使用C语言，实现九九乘法表（另附Python、Java、JavaScript实现方式）

文章目录 1. C语言实现1.1 思路1.2 代码实现 3.其他语言实现3.1 Python实现3.2 Java实现3.3 JavaScript实现 1. C语言实现 1.1 思路 九九乘法表图示&#xff1a; 思路如下&#xff1a;定义两层for循环即可实现九九乘法表 一共有9层&#xff0c;所以要定义一个变量i&#xff…...

编程日记 2023/8/26 21:27:11

[机缘参悟-102] ：IT人 - 管理的本质？管理人与从事技术的本质区别？人性、冰山模型、需求层次模型

感悟&#xff1a; 管理的本质是&#xff1a;学习各种管理理论、方法、技能&#xff0c;克服自身的人性缺点、预防他人人性的恶点、利用他人的人性特点拿到结果&#xff0c;从而完成组织、管理者的上司、管理者自身、管理者下属的目标。管理中的问题&#xff0c;80%以上都人性问…...

编程日记 2023/8/26 21:26:08

[论文阅读笔记26]Tracking Everything Everywhere All at Once

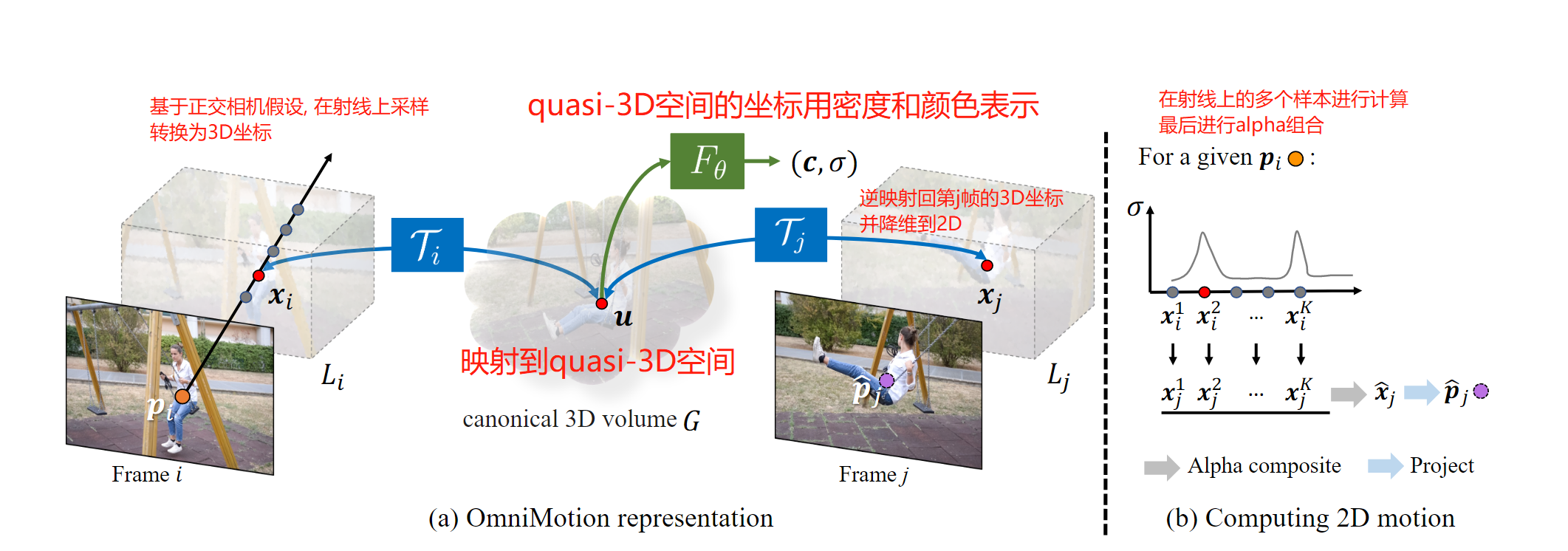
论文地址: 论文 代码地址: 代码 这是一篇效果极好的像素级跟踪的文章, 发表在ICCV2023, 可以非常好的应对遮挡等情形, 其根本的方法在于将2D点投影到一个伪3D(quasi-3D)空间, 然后再映射回去, 就可以在其他帧中得到稳定跟踪. 这篇文章的方法不是很好理解, 代码也刚开源, 做一…...

编程日记 2023/8/26 21:25:05

【Java 动态数据统计图】前后端对接数据格式（Map返回数组格式数据）六（120）

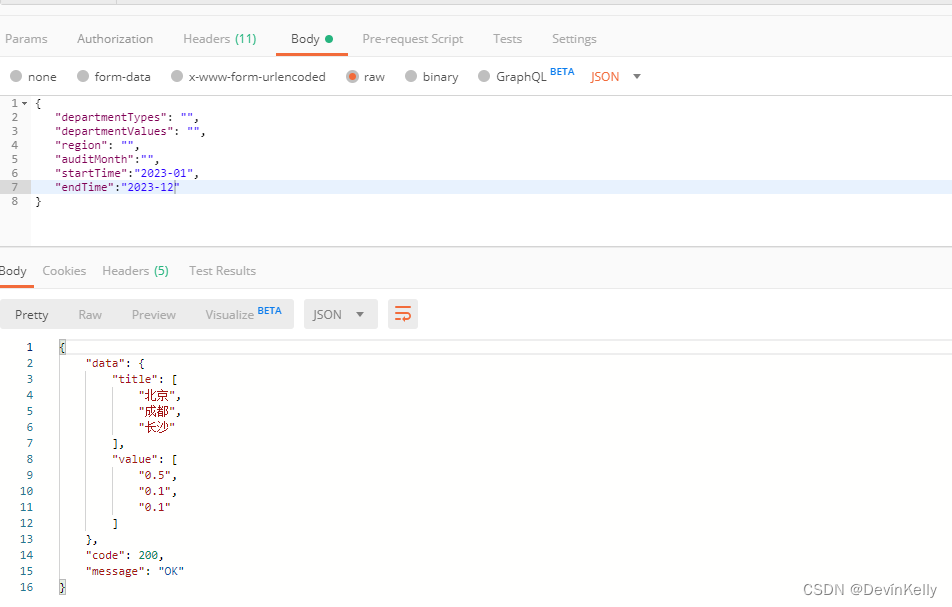
说明&#xff1a; 前端使用&#xff1a;vue3.0 前后端对接数据格式&#xff1a;无非就是前端把后端返回的数据处理为自己想要的格式&#xff0c;或者&#xff0c;后端给前端处理好想要的格式&#xff1b; 针对前后端的柱状图&#xff0c;趋势图等数据对接&#xff0c;前端一般需…...

编程日记 2023/8/26 21:24:03

❤ 给自己的mac系统上安装java环境

❤ 给自己的mac系统上安装java环境 &#x1f353; 作为前端工程师如何给自己的mac系统上安装java环境 &#x1f34e; 最近因为自己的一些项目需求&#xff0c;mac电脑上需要安装一些后台的java环境&#xff0c;用来跑后台的java程序&#xff0c;于是从一个前端工程师的角度安…...

编程日记 2023/8/26 21:23:01

Java-匿名类

介绍 匿名类是指没有名字的类&#xff0c;它对一个给定的类进行拓展&#xff0c;或者实现一个给定的接口。使用匿名类可以使得代码更加简洁、紧凑、模块程度更高。 实现方式及语法 匿名类有两种实现方式 继承一个类&#xff0c;重写其方法实现一个接口&#xff08;可以是多…...

编程日记 2023/8/26 21:21:59

Maven的超级POM

对于我们创建的一个maven工程&#xff0c;即便我们自己的pom.xm文件中没有明确指定一个父工程&#xff08;父POM&#xff09;&#xff0c;其实也默认继承了超级POM&#xff0c;就好比JAVA类继承Object类一样。 maven官网关于超级POM的介绍&#xff1a; https://maven.apache.o…...

编程日记 2023/8/26 21:20:55

软考高级系统架构设计师系列论文九十二：论新技术的引进

软考高级系统架构设计师系列论文九十二：论新技术的引进 一、摘要二、正文三、总结一、摘要 根据国家税务总局对税务系统内所有系统进行集成与整合的需求，我所在的开发单位组织了全国金税工程防伪税控系统网络版的升级开发工作。该项目工程浩大，要求在具有严格的安全、可靠性…...

编程日记 2023/8/26 21:19:53

vue使用Bootstrap的详细方法

要在Vue中使用Bootstrap&#xff0c;您可以按照以下步骤进行操作&#xff1a; 安装Bootstrap&#xff1a;首先&#xff0c;您需要安装Bootstrap。您可以使用npm或者yarn来安装Bootstrap。打开终端&#xff0c;并在项目的根目录中运行以下命令&#xff1a; npm install bootst…...

编程日记 2023/8/26 21:18:52

leetcode做题笔记103. 二叉树的锯齿形层序遍历

给你二叉树的根节点 root &#xff0c;返回其节点值的 锯齿形层序遍历 。&#xff08;即先从左往右&#xff0c;再从右往左进行下一层遍历&#xff0c;以此类推&#xff0c;层与层之间交替进行&#xff09;。 思路一&#xff1a;BFS #define N 2000int** zigzagLevelOrder(st…...

编程日记 2023/8/26 21:17:49

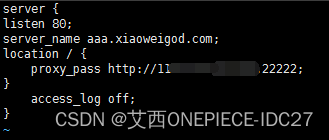
如果将PC电脑变成web服务器：利用Nignx反向代理绕过运营商对80端口封锁

如果将PC电脑变成web服务器&#xff1a;利用Nignx反向代理绕过运营商对80端口封锁 在上一篇文章中&#xff0c;我们已经实现了内网主机的多次端口映射&#xff0c;将内网主机的端口映射到了公网&#xff0c;可以通过公网访问该主机了。 因为电信的家庭宽带&#xff0c;默认是…...

编程日记 2023/8/26 21:16:47

Eureka:服务注册-信息配置-自我保护机制

首先在提供者服务下&#xff0c;添加一个依赖 <!-- Eureka --><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-eureka</artifactId><version>1.4.6.RELEASE</version><…...

编程日记 2023/8/26 21:15:46

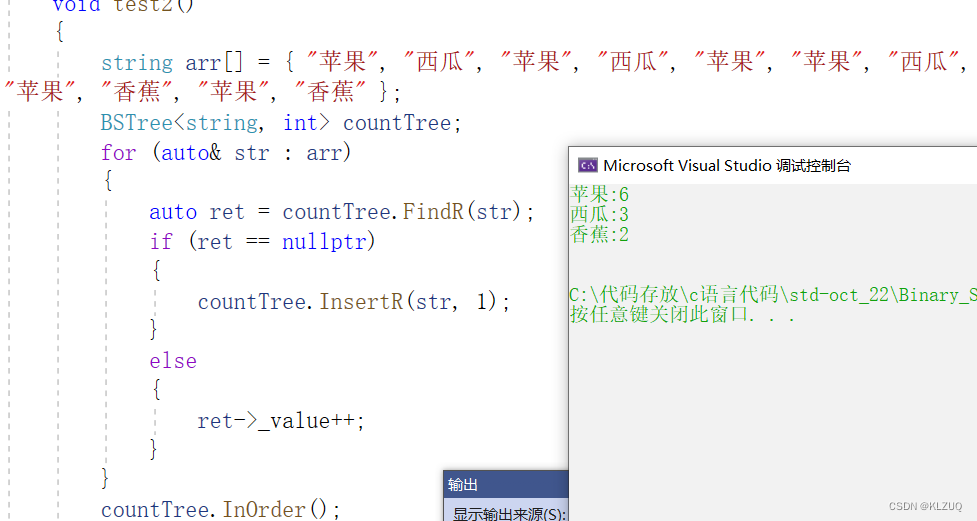
C++二叉树进阶

本期内容我们讲解二叉树的进阶知识&#xff0c;没有看过之前内容的小伙伴建议先看往期内容 二叉树-----补充_KLZUQ的博客-CSDN博客 目录 二叉搜索树 代码实现 基础框架 Insert Find Erase 析构函数 拷贝构造 赋值 二叉搜索树的应用 全部代码 二叉搜索树 二叉搜索树…...

编程日记 2023/8/26 21:14:43

layui tree组件取消勾选

layui(2.8.15) tree的api中&#xff0c;只有 tree.setChecked(id, idArr) 方法&#xff0c;没有取消勾选的方法。 我的需求是&#xff1a;勾选后做判断&#xff0c;如果不符合条件则取消勾选。 实现方法&#xff1a; 使用 tree的oncheck事件&#xff0c;在回调函数中做判断&…...

编程日记 2023/8/26 21:13:42

【Android基础面试题】ViewPager与ViewPager2的区别

ViewPager和ViewPager2是Android中用于实现滑动页面切换的控件。它们的主要区别如下&#xff1a; 实现方式 ViewPager2的内部实现是RecyclerView&#xff0c;而ViewPager是通过继承自ViewGroup实现的。因此&#xff0c;ViewPager2的性能更高。 滑动方向 ViewPager2可以实现横向…...

编程日记 2023/8/26 21:12:40

springCloudGateway网关配置

1.配置跨域支持 /*** 跨域支持*/ Configuration public class CorsConfig {Beanpublic CorsWebFilter corsFilter() {CorsConfiguration config new CorsConfiguration();config.addAllowedMethod("*");config.addAllowedOrigin("*");config.addAllowedH…...

编程日记 2023/8/26 21:10:36

kali 2023.3新增工具

在终端模拟器中运行 sudo apt update && sudo apt full-upgrade 命令来更新其安装 Kali Linux 2023.3 发布中包含了九个新工具&#xff0c;分别是&#xff1a; Calico&#xff1a;云原生网络和网络安全。 cri-tools&#xff1a;用于Kubelet容器运行时接口的命令行界面…...

编程日记 2023/8/26 21:09:34

W25Q64 驱动--基于SPI2接口

前言 &#xff08;1&#xff09;本系列是基于STM32的项目笔记&#xff0c;内容涵盖了STM32各种外设的使用&#xff0c;由浅入深。 &#xff08;2&#xff09;小编使用的单片机是STM32F105RCT6&#xff0c;项目笔记基于小编的实际项目&#xff0c;但是博客中的内容适用于各种单片…...

编程日记 2023/8/26 21:08:32

禁用无线键盘指定按键

文章目录 前言主体 前言 睡一觉把键盘压坏了一个按键,一开机键盘就自动打出这个字母,我在想用其他按键平替这个字母即可,使用软件修改内部的映射,那么使用autoHotkey软件是十分容易做到的 主体 letter_replace.ahk 创建一个如此命名的文件,然后输入命令即可 a::b 代表平替 a…...

编程日记 2023/8/26 21:07:30

分数规划（二分）

链接&#xff1a;登录—专业IT笔试面试备考平台_牛客网 来源&#xff1a;牛客网 题目描述 小咪是一个土豪手办狂魔&#xff0c;这次他去了一家店&#xff0c;发现了好多好多&#xff08;n个&#xff09;手办&#xff0c;但他是一个很怪的人&#xff0c;每次只想买k个手办&a…...

编程日记 2023/8/26 21:06:28

java_网络服务相关_gateway_nacos_feign区别联系

1. spring-cloud-starter-gateway 作用&#xff1a;作为微服务架构的网关&#xff0c;统一入口&#xff0c;处理所有外部请求。 核心能力&#xff1a; 路由转发&#xff08;基于路径、服务名等&#xff09;过滤器&#xff08;鉴权、限流、日志、Header 处理&#xff09;支持负…...

编程新知 2025/11/28 2:51:33

云启出海，智联未来｜阿里云网络「企业出海」系列客户沙龙上海站圆满落地

借阿里云中企出海大会的东风&#xff0c;以**「云启出海&#xff0c;智联未来&#xff5c;打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办&#xff0c;现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

编程新知 2026/1/30 0:00:28

【HarmonyOS 5.0】DevEco Testing：鸿蒙应用质量保障的终极武器

——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的​​一体化测试平台​​&#xff0c;覆盖应用全生命周期测试需求&#xff0c;主要提供五大核心能力&#xff1a; ​​测试类型​​​​检测目标​​​​关键指标​​功能体验基…...

编程新知 2026/1/28 8:17:53

工程地质软件市场：发展现状、趋势与策略建议

一、引言 在工程建设领域&#xff0c;准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具&#xff0c;正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

编程新知 2025/10/6 6:10:29

【决胜公务员考试】求职OMG——见面课测验1

2025最新版&#xff01;&#xff01;&#xff01;6.8截至答题&#xff0c;大家注意呀&#xff01; 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:&#xff08; B &#xff09; A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

编程新知 2025/11/8 16:25:01

Java多线程实现之Thread类深度解析

Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

编程新知 2025/8/28 21:52:02

python执行测试用例，allure报乱码且未成功生成报告

allure执行测试用例时显示乱码&#xff1a;‘allure’ &#xfffd;&#xfffd;&#xfffd;&#xfffd;&#xfffd;ڲ&#xfffd;&#xfffd;&#xfffd;&#xfffd;ⲿ&#xfffd;&#xfffd;&#xfffd;Ҳ&#xfffd;&#xfffd;&#xfffd;ǿ&#xfffd;&am…...

编程新知 2026/2/7 4:21:44

python报错No module named ‘tensorflow.keras‘

是由于不同版本的tensorflow下的keras所在的路径不同&#xff0c;结合所安装的tensorflow的目录结构修改from语句即可。 原语句&#xff1a; from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后&#xff1a; from tensorflow.python.keras.lay…...

编程新知 2025/9/24 7:39:50

JVM 内存结构 详解

内存结构 运行时数据区&#xff1a; Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器&#xff1a; ​ 线程私有&#xff0c;程序控制流的指示器&#xff0c;分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 ​ 每个线程都有一个程序计数…...

编程新知 2026/2/6 3:24:58

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档&#xff09;&#xff0c;如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下&#xff0c;风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

编程新知 2026/1/25 4:19:49