如何评估分类模型的好坏
如何评估分类模型的好坏
评估分类预测模型的质量,常用一个矩阵、三条曲线和六个指标。
- 一个矩阵:混淆矩阵;
- 三条曲线:ROC曲线、PR曲线、KS曲线;
- 六个指标:正确率Acc、查全率R、查准率P、F值、AUC、BEP值、KS值。
ROC曲线和AUC值
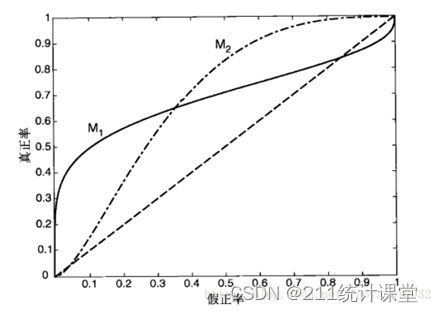
ROC曲线
ROC曲线(Receiver Operating Characteristic curve),即接收者操作特征曲线,是反映TPR和FPR的综合指标。
TPR = TP/(TP+FN),即正类中正确预测的百分比(查全率)。
FPR = FP/(FP+TN),即负类中错误预测的百分比(相当于误判率)。

ROC曲线是由点(TPR,FPR)组成的曲线,横坐标是FPR,而纵坐标是TPR。
显然,ROC曲线应该越靠近左上角越好,即表示查全率越高,而误判率越低。
一般来说,如果ROC是光滑的,那么基本可以判断没有太大的过拟合。
ROC曲线有助于比较不同分类器的相对性能。如下两个模型M1和M2,当FPR小于0.36时模型M1较好,而当FPR大于0.36时模型M2较好。
AUC值
与ROC曲线一同使用的,还有AUC指标。
AUC(Area Under Curve),其实就是ROC曲线下方的面积。
因为,ROC曲线一般都处于对角线的上方,即模型的效果应该比瞎猜(猜中的概率为50%)要好,所以AUC的取值范围一般是[0.5,1]。
AUC值越大,即ROC曲线越靠近左上角,其下方的面积越大,说明模型质量越高。
显然,由于ROC/AUC与混淆矩阵的TP、FP、TN、FN四个值都有关,所以,AUC是一个综合的评价指标。AUC值越大,也相当于TP和TN越大越好,FP和FN越小越好。
所以在大多数数据挖掘比赛中,要比较两个模型哪个会更优,AUC指标要比Accuracy指标常用得多,也比其它查全率R和查准率P要常用得多。
PR曲线和BEP值
PR曲线
PR曲线,反应的是查准率P和查全率R之间的关系。以P为横坐标,R作为纵坐标,就是PR网线。
P = TP/(TP+FP),即模型预测的正类中被正确预测的百分比。
R = FP/(FP+FN),即正类中被正确预测的百分比。
对于同一个分类模型,通过调整分类的阈值(从大到小变化),就可以得到不同的P-R值,即可画出PR曲线。
显然,我们要求P和R都应该是越高越好。如果一个模型的PR曲线被另一个模型的PR曲线所“包住”,则后者的性能要优于前者。如下图所示,模型A比模型C的性能要好,模型B比模型C的性能也要好。
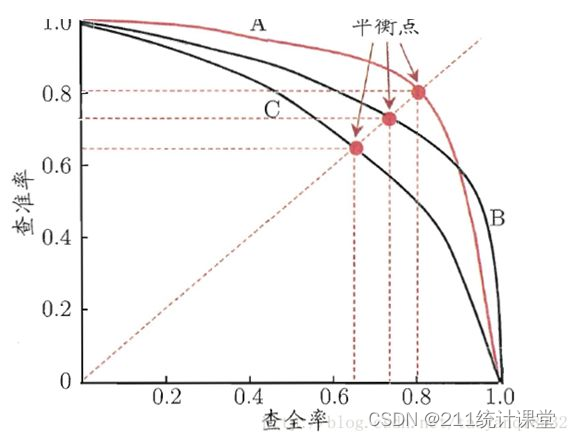
一般情况下,查准率和查全率这两个指标不可能兼顾。要想查全率R高,则模型需要输出更多的样本(极端地,返回全部样本,则查全率为100%);要想查准率P高,则要求在模型认为的正类中,尽量地选择少的概率高的样本。
BEP值
PR曲线中,一般要求P和R都越高越好,因此引入了一个指标BEP来表示模型的质量。
BEP(Break Even Point),亦称盈亏平衡点、保本点。即当查准率=查全率时的值。
在上图中,模型A和模型B,由于存在交叉,不太容易判断哪个模型会更好。如果使用BEP来判断,可知模型A的性能要优于模型B的性能。
显然,由于PR /BEP与混淆矩阵的TP、FP、FN三个值都有关(与TN无关),所以,BEP并不是一个综合的评价指标。
但是,即使是正样本非常少的情况下,PR表现的效果也比较好。也就是说,在正负样本不平衡的情况下,PR曲线比ROC曲线能更有效地反应分类器的好坏。
KS曲线和KS值
KS曲线
KS曲线(Kolmogorov-Smirnov),又叫洛伦兹曲线。以TPR和FPR分别分为纵轴,以阈值作为横轴,画出两条曲线。KS曲线反映的是在同一阈值下TPR和FPR的差值。

显然,我们希望的是TPR越高越好,而FPR越低越好,即要求两条折线离得越开越好,这说明模型对于正负样本区分度更好。
可以知道,KS曲线和ROC曲线一样,描述的都是TPR和FPR的关系,只是横坐标的取法不一样。
KS值
考虑到量化,所以将TPR和FPR折线的最远距离作为KS值,即KS=max(TPR-FPR),作为模型的分区度。
K-S值越大,表示评分模型能够将“好客户”、“坏客户”区分开来的程度越大。
一般认为:
1) 当KS<0.2时,模型无鉴别能力
2) 在0.2~0.4之间,模型勉强接受,需要考虑优化
3) 在0.4~0.5之间,模型有区别能力
4) 在0.5~0.6之间,模型有较好的区别能力
5) 在0.6~0.7之间,模型有非常好的区别能力
6) 当KS>0.75时,要检验模型是否过拟合
由于KS值主要是体现模型中差异的最大的一个分段,因此适合于找阈值。像信用评分卡中,就比较适合使用KS值来评估,寻找出最大的区分度阈值。
曲线对比
一般来说,ROC曲线会更稳定,在正负样本足够(样本均衡)的情况下,ROC曲线会比较稳定,能够反映模型的整体质量。当样本不平衡时,特别是正样本极少时,ROC曲线并不准确。
在样本不均衡时,特别是正样本数远小于负样本数时,采用PR曲线会更合适。
而KS曲线,只是反映出哪个分段的区分度是最大的,而不能反映出总体的效果。所以,KS曲线往往只用在寻找区分的最佳阈值(比如信用评分卡中的审批阈值)。
一般情况下,最好能够综合考虑上述的三种曲线以及三个指标,这样对模型有一个全面的质量评估。
相关文章:

如何评估分类模型的好坏
如何评估分类模型的好坏 评估分类预测模型的质量,常用一个矩阵、三条曲线和六个指标。 一个矩阵:混淆矩阵;三条曲线:ROC曲线、PR曲线、KS曲线;六个指标:正确率Acc、查全率R、查准率P、F值、AUC、BEP值、KS…...

● 84.柱状图中最大的矩形
84.柱状图中最大的矩形 class Solution { public:int largestRectangleArea(vector<int>& heights) {stack<int>st;heights.insert(heights.begin(),0);heights.push_back(0);st.push(0);int res0;for(int i1;i<heights.size();i){while(heights[i]<heig…...

未检查的转换: ‘java.lang.Object‘ 转换为 ‘java.util.List
fastjson方式 Object object ... // 获取待转换的objectList<WbsCategory> list JSON.parseObject(JSON.toJSONString(object), new TypeReference<List<WbsCategory>>() {}); 在这个示例中,我们使用JSON.toJSONString()将object对象转换…...
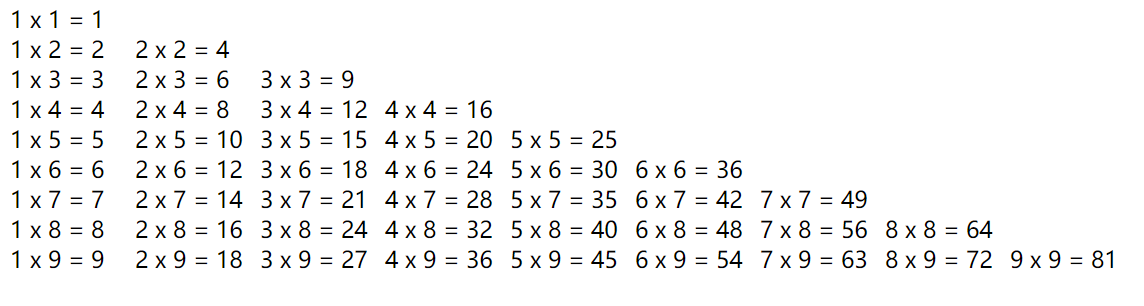
【C语言】使用C语言,实现九九乘法表(另附Python、Java、JavaScript实现方式)
文章目录 1. C语言实现1.1 思路1.2 代码实现 3.其他语言实现3.1 Python实现3.2 Java实现3.3 JavaScript实现 1. C语言实现 1.1 思路 九九乘法表图示: 思路如下:定义两层for循环即可实现九九乘法表 一共有9层,所以要定义一个变量iÿ…...

[机缘参悟-102] :IT人 - 管理的本质?管理人与从事技术的本质区别?人性、冰山模型、需求层次模型
感悟: 管理的本质是:学习各种管理理论、方法、技能,克服自身的人性缺点、预防他人人性的恶点、利用他人的人性特点拿到结果,从而完成组织、管理者的上司、管理者自身、管理者下属的目标。管理中的问题,80%以上都人性问…...
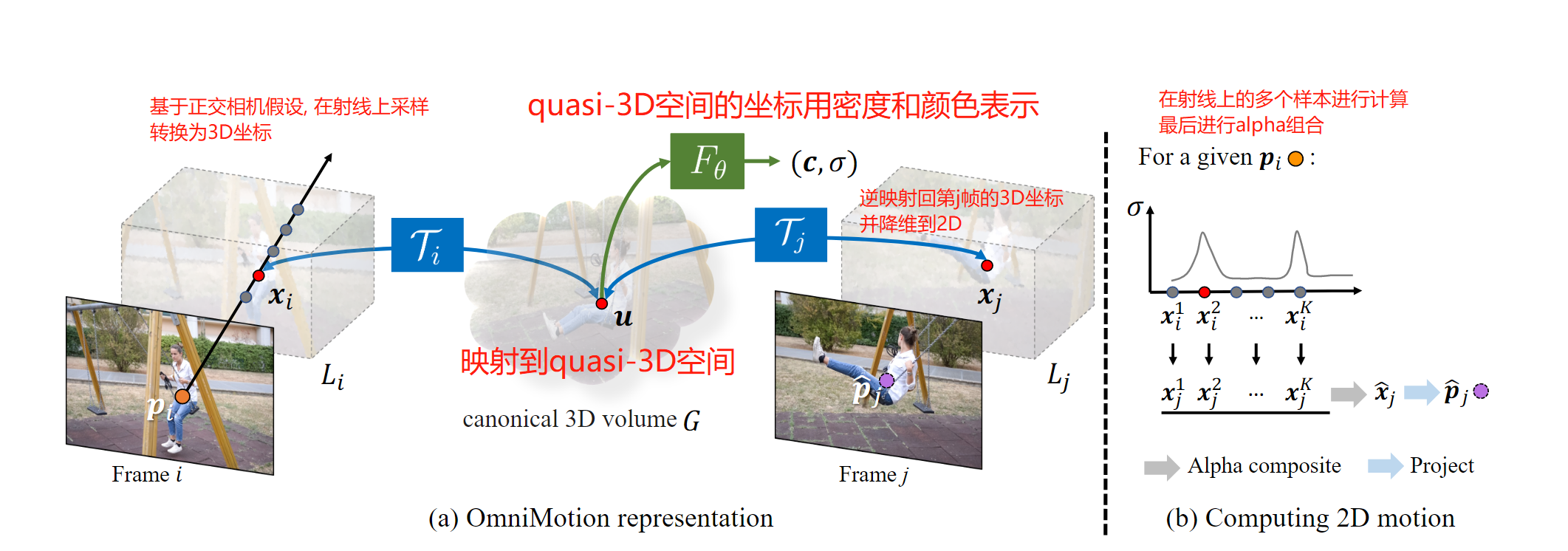
[论文阅读笔记26]Tracking Everything Everywhere All at Once
论文地址: 论文 代码地址: 代码 这是一篇效果极好的像素级跟踪的文章, 发表在ICCV2023, 可以非常好的应对遮挡等情形, 其根本的方法在于将2D点投影到一个伪3D(quasi-3D)空间, 然后再映射回去, 就可以在其他帧中得到稳定跟踪. 这篇文章的方法不是很好理解, 代码也刚开源, 做一…...
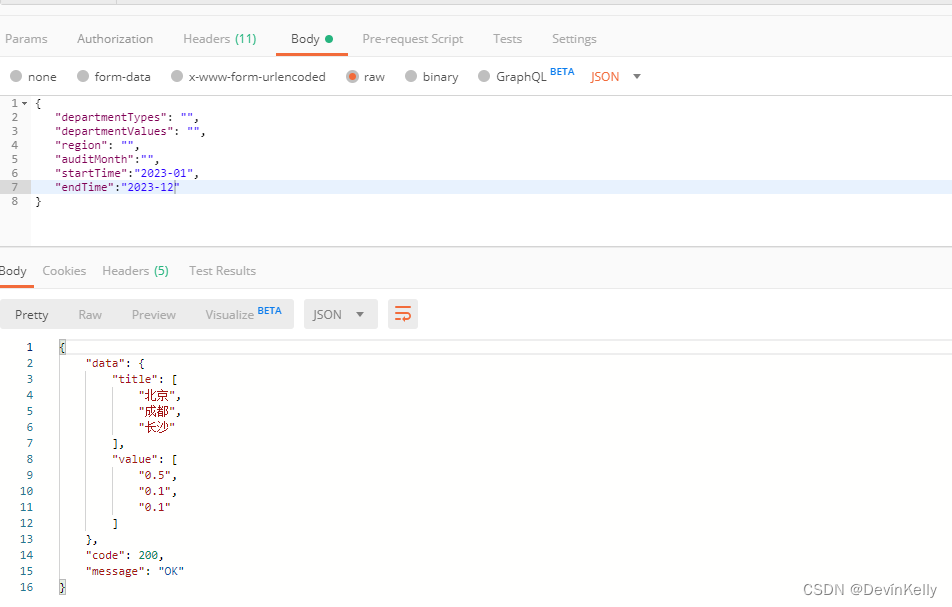
【Java 动态数据统计图】前后端对接数据格式(Map返回数组格式数据)六(120)
说明: 前端使用:vue3.0 前后端对接数据格式:无非就是前端把后端返回的数据处理为自己想要的格式,或者,后端给前端处理好想要的格式; 针对前后端的柱状图,趋势图等数据对接,前端一般需…...
❤ 给自己的mac系统上安装java环境
❤ 给自己的mac系统上安装java环境 🍓 作为前端工程师如何给自己的mac系统上安装java环境 🍎 最近因为自己的一些项目需求,mac电脑上需要安装一些后台的java环境,用来跑后台的java程序,于是从一个前端工程师的角度安…...

Java-匿名类
介绍 匿名类是指没有名字的类,它对一个给定的类进行拓展,或者实现一个给定的接口。使用匿名类可以使得代码更加简洁、紧凑、模块程度更高。 实现方式及语法 匿名类有两种实现方式 继承一个类,重写其方法实现一个接口(可以是多…...
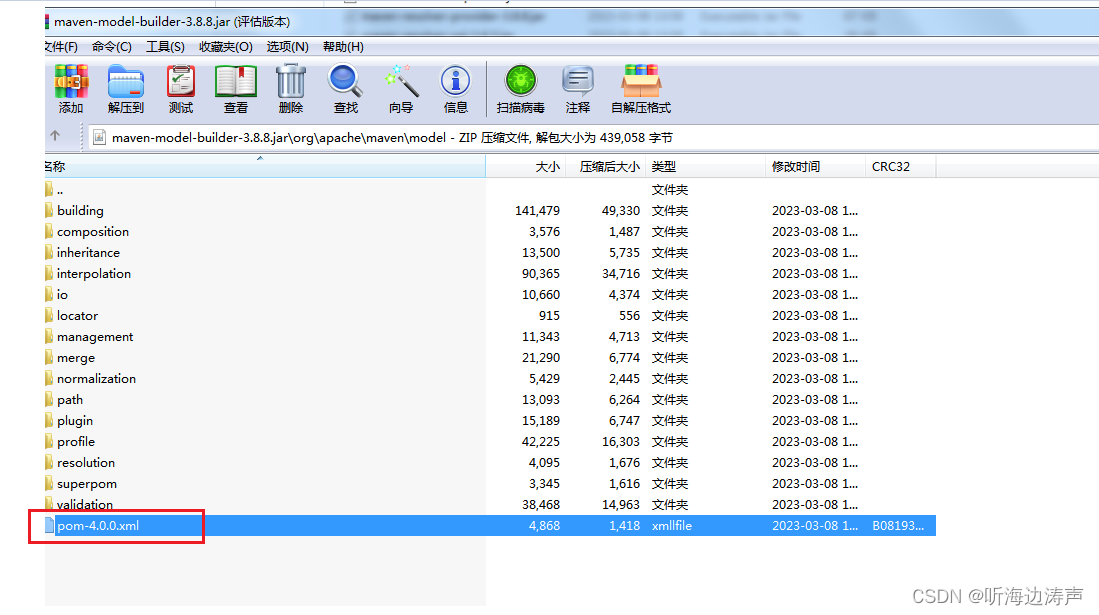
Maven的超级POM
对于我们创建的一个maven工程,即便我们自己的pom.xm文件中没有明确指定一个父工程(父POM),其实也默认继承了超级POM,就好比JAVA类继承Object类一样。 maven官网关于超级POM的介绍: https://maven.apache.o…...

软考高级系统架构设计师系列论文九十二:论新技术的引进
软考高级系统架构设计师系列论文九十二:论新技术的引进 一、摘要二、正文三、总结一、摘要 根据国家税务总局对税务系统内所有系统进行集成与整合的需求,我所在的开发单位组织了全国金税工程防伪税控系统网络版的升级开发工作。该项目工程浩大,要求在具有严格的安全、可靠性…...

vue使用Bootstrap的详细方法
要在Vue中使用Bootstrap,您可以按照以下步骤进行操作: 安装Bootstrap:首先,您需要安装Bootstrap。您可以使用npm或者yarn来安装Bootstrap。打开终端,并在项目的根目录中运行以下命令: npm install bootst…...

leetcode做题笔记103. 二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。 思路一:BFS #define N 2000int** zigzagLevelOrder(st…...
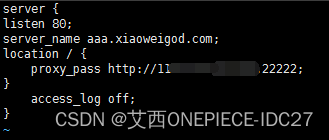
如果将PC电脑变成web服务器:利用Nignx反向代理绕过运营商对80端口封锁
如果将PC电脑变成web服务器:利用Nignx反向代理绕过运营商对80端口封锁 在上一篇文章中,我们已经实现了内网主机的多次端口映射,将内网主机的端口映射到了公网,可以通过公网访问该主机了。 因为电信的家庭宽带,默认是…...

Eureka:服务注册-信息配置-自我保护机制
首先在提供者服务下,添加一个依赖 <!-- Eureka --><dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-eureka</artifactId><version>1.4.6.RELEASE</version><…...
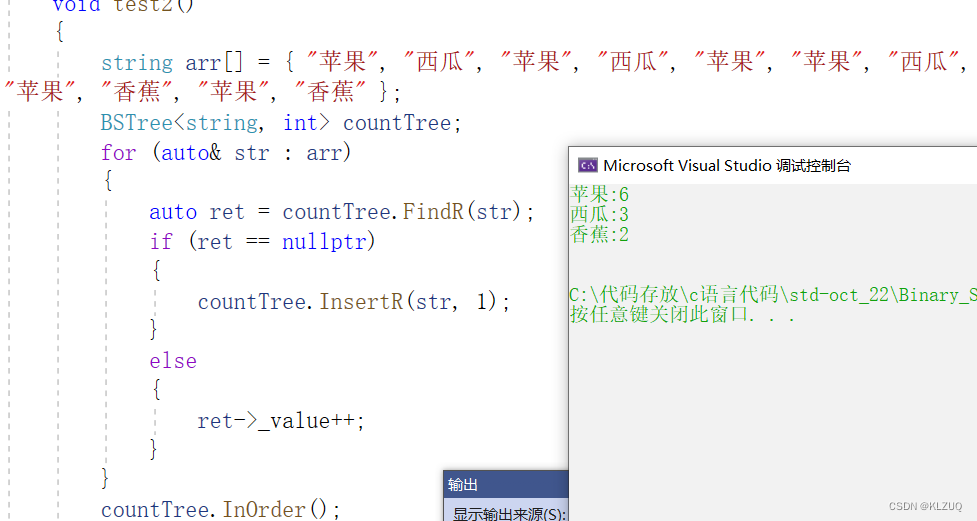
C++二叉树进阶
本期内容我们讲解二叉树的进阶知识,没有看过之前内容的小伙伴建议先看往期内容 二叉树-----补充_KLZUQ的博客-CSDN博客 目录 二叉搜索树 代码实现 基础框架 Insert Find Erase 析构函数 拷贝构造 赋值 二叉搜索树的应用 全部代码 二叉搜索树 二叉搜索树…...

layui tree组件取消勾选
layui(2.8.15) tree的api中,只有 tree.setChecked(id, idArr) 方法,没有取消勾选的方法。 我的需求是:勾选后做判断,如果不符合条件则取消勾选。 实现方法: 使用 tree的oncheck事件,在回调函数中做判断&…...

【Android基础面试题】ViewPager与ViewPager2的区别
ViewPager和ViewPager2是Android中用于实现滑动页面切换的控件。它们的主要区别如下: 实现方式 ViewPager2的内部实现是RecyclerView,而ViewPager是通过继承自ViewGroup实现的。因此,ViewPager2的性能更高。 滑动方向 ViewPager2可以实现横向…...

springCloudGateway网关配置
1.配置跨域支持 /*** 跨域支持*/ Configuration public class CorsConfig {Beanpublic CorsWebFilter corsFilter() {CorsConfiguration config new CorsConfiguration();config.addAllowedMethod("*");config.addAllowedOrigin("*");config.addAllowedH…...

kali 2023.3新增工具
在终端模拟器中运行 sudo apt update && sudo apt full-upgrade 命令来更新其安装 Kali Linux 2023.3 发布中包含了九个新工具,分别是: Calico:云原生网络和网络安全。 cri-tools:用于Kubelet容器运行时接口的命令行界面…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
