深度学习基本理论下篇:(梯度下降/卷积/池化/归一化/AlexNet/归一化/Dropout/卷积核)、深度学习面试
深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播)
深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播)、深度学习面试_会害羞的杨卓越的博客-CSDN博客
18、 请说明Momentum、AdaGrad、Adam梯度下降法的特点
Momentum、AdaGrad、Adam是针对SGD梯度下降算法的缺点的改进算法。在SGD算法中,如果函数的形状非均向(参数大小差异较大),SGD的搜索路径会呈“之字形”移动,搜索效率较低。如下图所示:
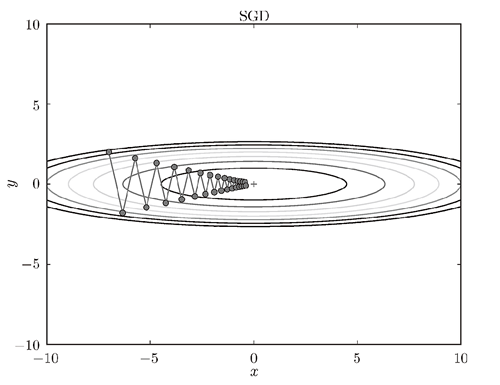
1)Momentum
Momentum是“动量”的意思,和物理有关。用数学式表示Momentum方法,如下所示:
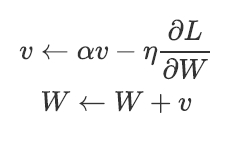
其中,W表示要更新的权重参数,∂L/∂w表示W的梯度,η表示学习率,v对应物理上的速度。在物体不受任何力时,该项承担使物体逐渐减速的任务(α设定为0.9之类的值),对应物理上的地面摩擦或空气阻力。和SGD相比,我们发现“之”字形的“程度”减轻了。这是因为,虽然x轴方向上受到的力非常小,但是一直在同一方向上受力,所以朝同一个方向会有一定的加速。反过来,虽然y轴方向上受到的力很大,但是因为交互地受到正方向和反方向的力,它们会互相抵消,所以y轴方向上的速度不稳定。因此,和SGD时的情形相比,可以更快地朝x轴方向靠近,减弱“之”字形的变动程度。如下图所示:
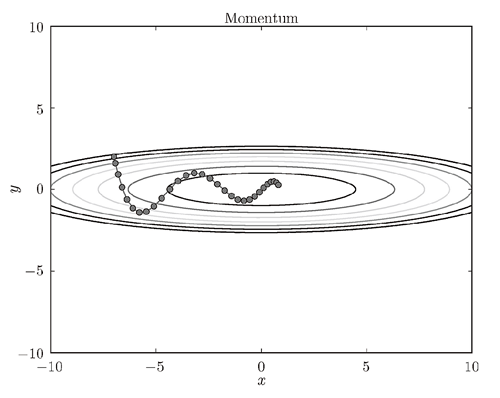
2)AdaGrad
AdaGrad会为参数的每个元素适当地调整学习率,与此同时进行学习(AdaGrad的Ada来自英文单词Adaptive,即“适当的”的意思),其表达式为:
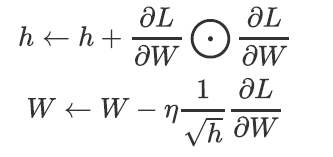
其中,W表示要更新的权重参数,$\frac{\partial L}{\partial W}$表示W的梯度,$\eta$表示学习率,$\frac{\partial L} {\partial W} \bigodot \frac{\partial L} {\partial W}$表示所有梯度值的平方和。在参数更新时,通过乘以$\frac{1}{\sqrt h}$就可以调整学习的尺度。这意味着,参数的元素中变动较大(被大幅更新)的元素的学习率将变小。也就是说,可以按参数的元素进行学习率衰减,使变动大的参数的学习率逐渐减小。其收敛路径如下图所示:
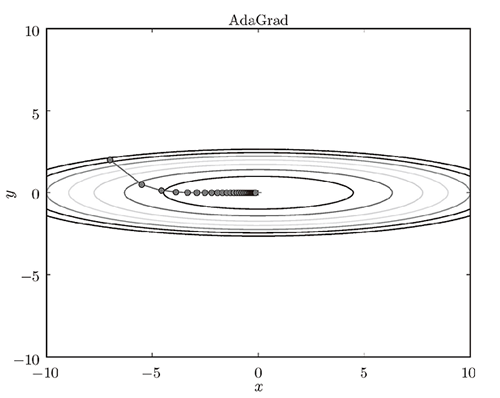
3)Adam
Adam是2015年提出的新方法。它的理论有些复杂,直观地讲,就是融合了Momentum和AdaGrad的方法。通过组合前面两个方法的优点,有望实现参数空间的高效搜索。其收敛路径如下图所:
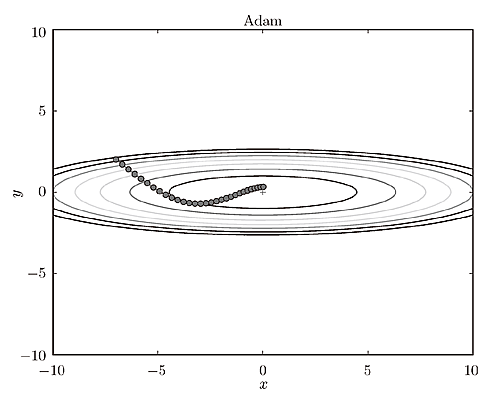
以下是几种梯度下降算法的收敛情况对比:
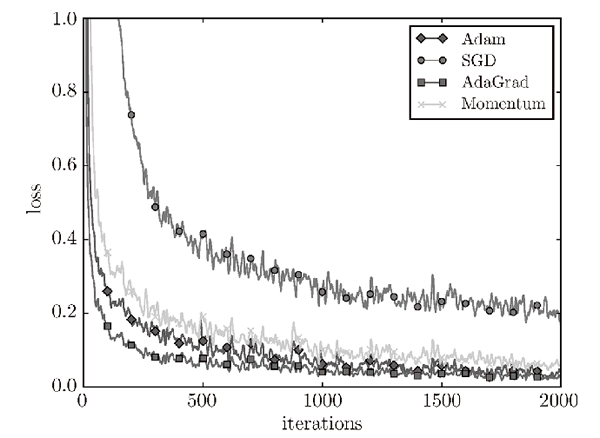
19. 什么是卷积函数
卷积函数指一个函数和另一个函数在某个维度上的加权“叠加”作用,其表达式为:
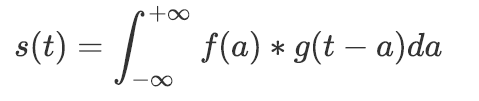
离散化卷积函数表示为:
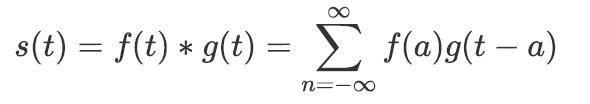
20. 二维卷积运算中,输出矩阵大小与输入矩阵、卷积核大小、步幅、填充的关系?
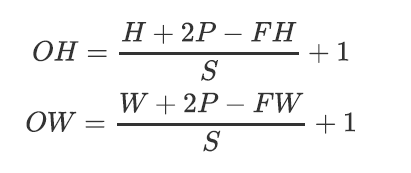
- OH:输出高
- OW:输出宽
- H:输入高
- W:输入宽
- P:padding层数
- FH:卷积核高
- FW:卷积核宽
- S:步长
21. 什么是池化,池化层的作用是什么
也称子采样层或下采样层(Subsampling Layer),目的是缩小高、长方向上的空间的运算,以降低计算量,提高泛化能力。
22. 什么是最大池化、平均池化
最大池化:取池化区域内的最大值作为池化输出
平均池化:取池化区域内的平均值作为池化输出
23. 池化层有什么特征
1)没有要学习的参数
2)通道数不发生变化
3)对微小的变化具有鲁棒性
24. 什么是归一化, 为什么要进行归一化
1)归一化的含义。归一化是指归纳统一样本的统计分布性。归一化在 $ 0-1$ 之间是统计的概率分布,归一化在$ -1--+1$ 之间是统计的坐标分布
2)归一化处理的目的
- 为了后面数据处理的方便,归一化的确可以避免一些不必要的数值问题
- 为了程序运行时收敛加快
- 统一量纲。样本数据的评价标准不一样,需要对其量纲化,统一评价标准
- 避免神经元饱和。当神经元的激活在接近 0 或者 1 时会饱和,在这些区域,梯度几乎为 0,这样,在反向传播过程中,局部梯度就会接近 0,这会有效地“杀死”梯度。
25. 什么是批量归一化,其优点是什么
1)批量归一化(Batch Normalization,简写BN)指在神经网络中间层也进行归一化处理,使训练效果更好的方法,就是批量归一化。
2)优点
- 减少了人为选择参数。在某些情况下可以取消 dropout 和 L2 正则项参数,或者采取更小的 L2 正则项约束参数;
- 减少了对学习率的要求。现在我们可以使用初始很大的学习率或者选择了较小的学习率,算法也能够快速训练收敛;
- 可以不再使用局部响应归一化(BN 本身就是归一化网络) ;
- 破坏原来的数据分布,一定程度上缓解过拟合;
- 减少梯度消失,加快收敛速度,提高训练精度。
26. 请列举AlexNet的特点
- 使用ReLU作为激活函数,并验证其效果在较深的网络超过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度消失问题
- 使用Dropout(丢弃学习)随机忽略一部分神经元防止过拟合
- 在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化,AlexNet全部使用最大池化,避免平均池化的模糊化效果
- 提出了LRN(Local Response Normalization,局部正规化)层,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力
- 使用CUDA加速深度卷积网络的训练,利用GPU强大的并行计算能力,处理神经网络训练时大量的矩阵运算
27. 什么是dropout操作,dropout的工作原理?
1)定义
Dropout是用于深度神经网络防止过拟合的一种方式,在神经网络训练过程中,通过忽略一定比例
的特征检测器(让一半的隐层节点值为0),可以明显地减少过拟合现象。这种方式可以减少特征检测器(隐层节点)间的相互作用,检测器相互作用是指某些检测器依赖其他检测器才能发挥作用。简单来说,在前向传播的时候,让某个神经元的激活值以一定的概率P停止工作,这样可以使模型泛化性更强,因为它不会太依赖某些局部的特征。
2)dropout工作原理
假设我们要训练这样一个网络,结构如左图所示:
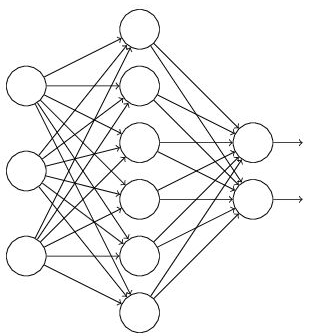
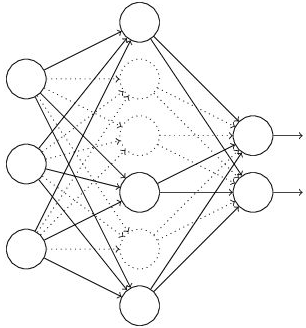
输入是x输出是y,正常的流程是:我们首先把x通过网络前向传播,然后把误差反向传播以决定如何更新参数让网络进行学习。使用Dropout之后,过程变成如右图:
(1)首先随机(临时)删掉网络中一半的隐藏神经元,输入输出神经元保持不变(上图中虚线表示临时被删除的神经元)
(2) 然后把输入x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后,在没有被删除的神经元上按照随机梯度下降法更新对应的参数(w,b)
(3)然后继续重复以下过程:
- 恢复被删掉的神经元(此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
- 从隐藏层神经元中随机选择一定比率子集临时删除掉(备份被删除神经元的参数)
- 对一小批训练样本,先前向传播然后反向传播损失并根据随机梯度下降法更新参数(w,b) (没有被删除的那一部分参数得到更新,删除的神经元参数保持被删除前的结果)
3)为什么dropout能避免过拟合
(1)取平均作用。不同的网络可能产生不同的过拟合,取平均则有可能让一些“相反的”拟合互相抵消。
(2)减少神经元之间复杂的共适应关系。因为dropout程序导致两个神经元不一定每次都在一个
dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征
仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ,这些特征在其它的神经元
的随机子集中也存在。
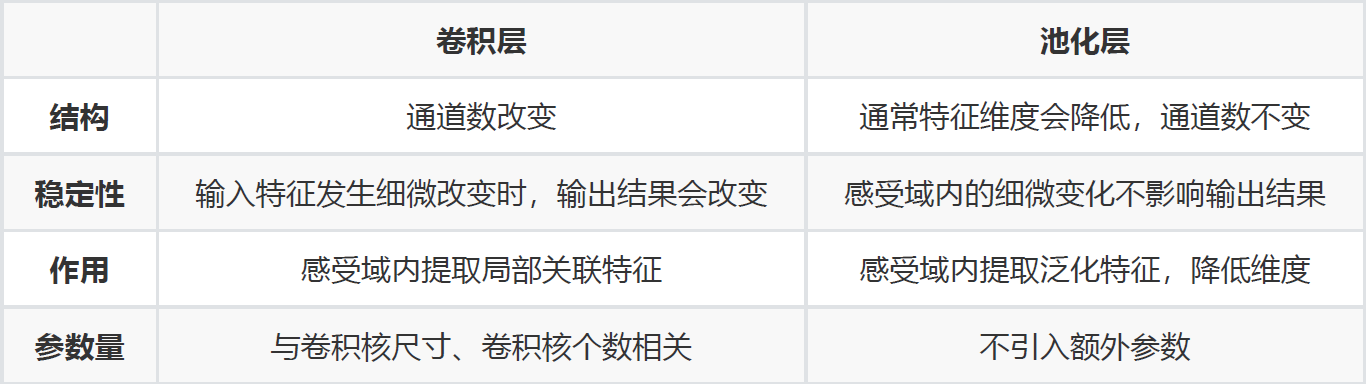
28. 卷积层和池化层有什么区别
卷积层和池化层在结构上具有一定的相似性,都是对感受域内的特征进行提取,并且根据步长设置
获取到不同维度的输出,但是其内在操作是有本质区别的,如下表所示:
 29. 如何选择卷积核大小
29. 如何选择卷积核大小
在早期的卷积神经网络中(如LeNet-5、AlexNet),用到了一些较大的卷积核($11\times11$),受限于当时的计算能力和模型结构的设计,无法将网络叠加得很深,因此卷积网络中的卷积层需要设置较大的卷积核以获取更大的感受域。但是这种大卷积核反而会导致计算量大幅增加,不利于训练更深层的模型,相应的计算性能也会降低。后来的卷积神经网络(VGG、GoogLeNet等),发现通过堆叠2个$3\times 3$卷积核可以获得与$5\times 5$卷积核相同的感受视野,同时参数量会更少($3×3×2+1$ < $ 5×5×1+1$),$3\times 3$卷积核被广泛应用在许多卷积神经网络中。因此可以认为,在大多数情况下通过堆叠较小的卷积核比直接采用单个更大的卷积核会更加有效。
30. 如何提高图像分类的准确率
1)样本优化
增大样本数量
数据增强:形态、色彩、噪声扰动
2)参数优化
批量正则化
变化学习率
权重衰减
3)模型优化
增加网络模型深度
更换更复杂的模型
深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播)
深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播)、深度学习面试_会害羞的杨卓越的博客-CSDN博客
相关文章:

深度学习基本理论下篇:(梯度下降/卷积/池化/归一化/AlexNet/归一化/Dropout/卷积核)、深度学习面试
深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播) 深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播)、深度学习面试_会害羞的杨…...
)
[Ubuntu 20.04] 通过udev规则修改网卡名称(例如eth0)
在 Ubuntu 20.04 操作系统中,默认情况下,网卡接口名称采用了一种较为复杂的命名方式(如 enp0s3、eth0 等)。然而,有时候我们可能更希望使用更简洁和易于识别的名称来标识不同的网络接口。那么如何在 Ubuntu 20.04 中修改网卡接口的名称,以满足个性化需求。 步骤一:查看当…...

Java“牵手”根据关键词搜索(分类搜索)lazada商品列表页面数据获取方法,lazadaAPI实现批量商品数据抓取示例
lazada商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取lazada商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问lazada商城的网页来获取商品详情信息。以下是两种常用方法的介…...
Java—实现多线程程序 | 入门
目录 一、前言 二、基本概念 进程 线程 三、Java多线程实现 java.lang.Thread类 获取线程名字及对象 获取main进程名 Thread currentThread() 四、线程优先级 设置优先级 一、前言 前期入门学习的代码中,全部都是单线的程序,也就是从头到尾…...

8.5 【C语言】指向函数的指针
8.5.1 什么是函数的指针 每次调用函数时都从该地址入口开始执行此段函数代码。函数名代表函数的起始地址。 8.5.2 用函数指针变量调用函数 例8.22 用函数求整数a和b中的大者 解题思路:在主函数调用max函数,除了可以通过函数名调用外,还可…...

C++实现字符串的逆置
目录 C和C的区别 【1】C对C的扩充 【2】C对C的兼容 第一个C程序 【1】hello world 【2】cout标准输出流对象 i)介绍 ii)运算 iii)cout的使用 iv)使用cout指定格式的输出 练习:1、输出斐波那契的前10项。 【3】…...

论Spring或Spring Boot的花式扩展
文章目录 引言扩展点讲述花式扩展之自动配置类花式扩展之实现接口实现方式样例 花式扩展之自定义starterImport方式SpringFactories方式 总结鸣谢 引言 Spring Boot是一个高度可定制的框架,旨在帮助开发者快速创建、配置和管理他们的应用程序 扩展点讲述 Spring Bo…...

如何评估分类模型的好坏
如何评估分类模型的好坏 评估分类预测模型的质量,常用一个矩阵、三条曲线和六个指标。 一个矩阵:混淆矩阵;三条曲线:ROC曲线、PR曲线、KS曲线;六个指标:正确率Acc、查全率R、查准率P、F值、AUC、BEP值、KS…...

● 84.柱状图中最大的矩形
84.柱状图中最大的矩形 class Solution { public:int largestRectangleArea(vector<int>& heights) {stack<int>st;heights.insert(heights.begin(),0);heights.push_back(0);st.push(0);int res0;for(int i1;i<heights.size();i){while(heights[i]<heig…...

未检查的转换: ‘java.lang.Object‘ 转换为 ‘java.util.List
fastjson方式 Object object ... // 获取待转换的objectList<WbsCategory> list JSON.parseObject(JSON.toJSONString(object), new TypeReference<List<WbsCategory>>() {}); 在这个示例中,我们使用JSON.toJSONString()将object对象转换…...
【C语言】使用C语言,实现九九乘法表(另附Python、Java、JavaScript实现方式)
文章目录 1. C语言实现1.1 思路1.2 代码实现 3.其他语言实现3.1 Python实现3.2 Java实现3.3 JavaScript实现 1. C语言实现 1.1 思路 九九乘法表图示: 思路如下:定义两层for循环即可实现九九乘法表 一共有9层,所以要定义一个变量iÿ…...

[机缘参悟-102] :IT人 - 管理的本质?管理人与从事技术的本质区别?人性、冰山模型、需求层次模型
感悟: 管理的本质是:学习各种管理理论、方法、技能,克服自身的人性缺点、预防他人人性的恶点、利用他人的人性特点拿到结果,从而完成组织、管理者的上司、管理者自身、管理者下属的目标。管理中的问题,80%以上都人性问…...
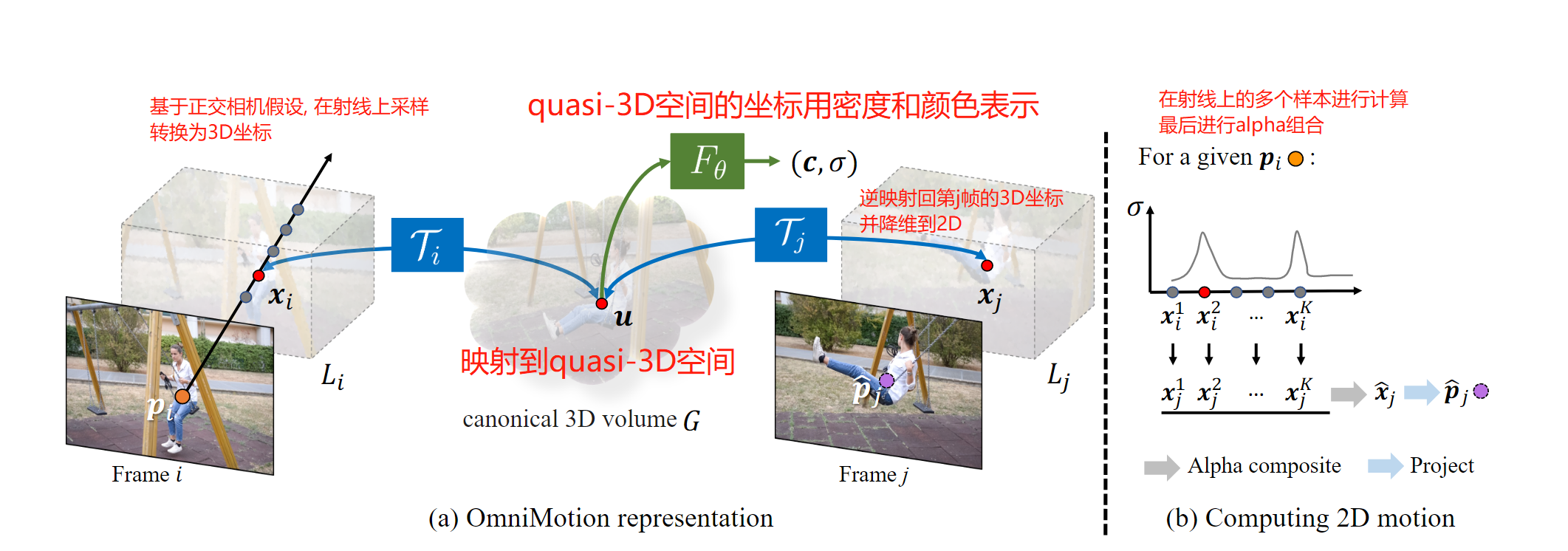
[论文阅读笔记26]Tracking Everything Everywhere All at Once
论文地址: 论文 代码地址: 代码 这是一篇效果极好的像素级跟踪的文章, 发表在ICCV2023, 可以非常好的应对遮挡等情形, 其根本的方法在于将2D点投影到一个伪3D(quasi-3D)空间, 然后再映射回去, 就可以在其他帧中得到稳定跟踪. 这篇文章的方法不是很好理解, 代码也刚开源, 做一…...
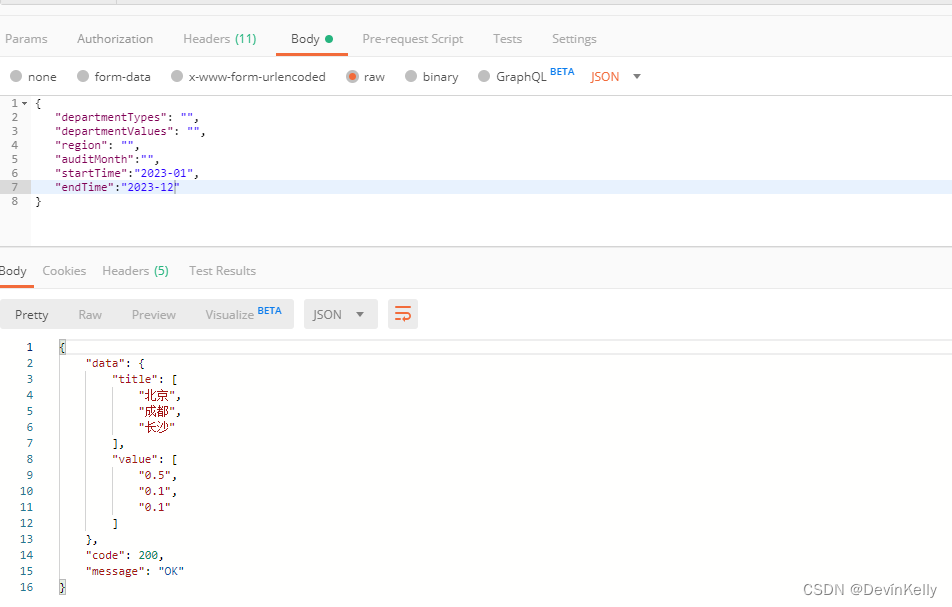
【Java 动态数据统计图】前后端对接数据格式(Map返回数组格式数据)六(120)
说明: 前端使用:vue3.0 前后端对接数据格式:无非就是前端把后端返回的数据处理为自己想要的格式,或者,后端给前端处理好想要的格式; 针对前后端的柱状图,趋势图等数据对接,前端一般需…...
❤ 给自己的mac系统上安装java环境
❤ 给自己的mac系统上安装java环境 🍓 作为前端工程师如何给自己的mac系统上安装java环境 🍎 最近因为自己的一些项目需求,mac电脑上需要安装一些后台的java环境,用来跑后台的java程序,于是从一个前端工程师的角度安…...

Java-匿名类
介绍 匿名类是指没有名字的类,它对一个给定的类进行拓展,或者实现一个给定的接口。使用匿名类可以使得代码更加简洁、紧凑、模块程度更高。 实现方式及语法 匿名类有两种实现方式 继承一个类,重写其方法实现一个接口(可以是多…...
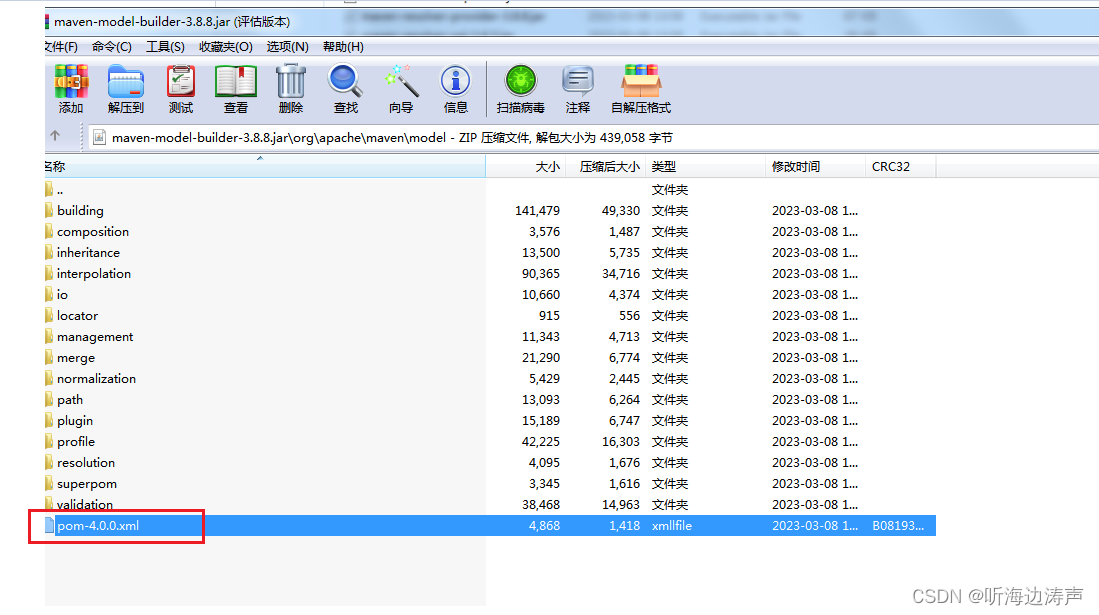
Maven的超级POM
对于我们创建的一个maven工程,即便我们自己的pom.xm文件中没有明确指定一个父工程(父POM),其实也默认继承了超级POM,就好比JAVA类继承Object类一样。 maven官网关于超级POM的介绍: https://maven.apache.o…...

软考高级系统架构设计师系列论文九十二:论新技术的引进
软考高级系统架构设计师系列论文九十二:论新技术的引进 一、摘要二、正文三、总结一、摘要 根据国家税务总局对税务系统内所有系统进行集成与整合的需求,我所在的开发单位组织了全国金税工程防伪税控系统网络版的升级开发工作。该项目工程浩大,要求在具有严格的安全、可靠性…...

vue使用Bootstrap的详细方法
要在Vue中使用Bootstrap,您可以按照以下步骤进行操作: 安装Bootstrap:首先,您需要安装Bootstrap。您可以使用npm或者yarn来安装Bootstrap。打开终端,并在项目的根目录中运行以下命令: npm install bootst…...

leetcode做题笔记103. 二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。 思路一:BFS #define N 2000int** zigzagLevelOrder(st…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...
