当前位置： 首页 > news >正文

推荐系统[八]算法实践总结V1：淘宝逛逛and阿里飞猪个性化推荐：召回算法实践总结【冷启动召回、复购召回、用户行为召回等算法实战】

news 2026/2/9 10:03:49

0.前言：召回排序流程策略算法简介

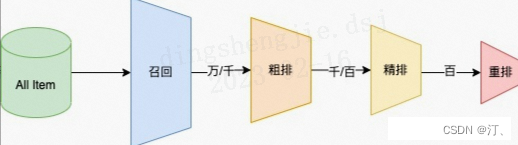
在这里插入图片描述
推荐可分为以下四个流程，分别是召回、粗排、精排以及重排：

  1. 召回是源头，在某种意义上决定着整个推荐的天花板；
  2. 粗排是初筛，一般不会上复杂模型；
  3. 精排是整个推荐环节的重中之重，在特征和模型上都会做的比较复杂；
  4. 重排，一般是做打散或满足业务运营的特定强插需求，同样不会使用复杂模型；

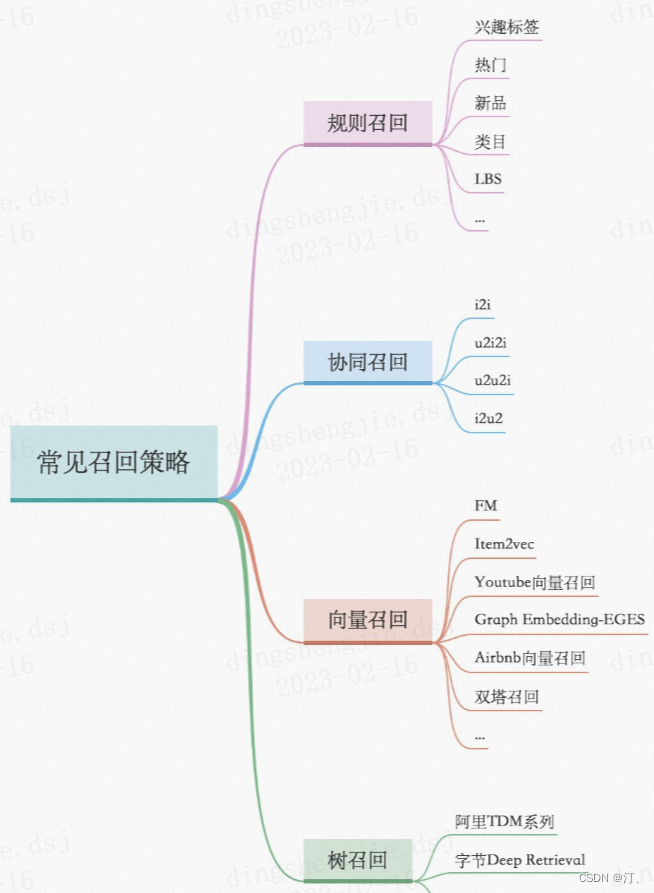
  • 召回层：召回解决的是从海量候选item中召回千级别的item问题

    • 统计类，热度，LBS；
    • 协同过滤类，UserCF、ItemCF；
    • U2T2I，如基于user tag召回；
    • I2I类，如Embedding（Word2Vec、FastText），GraphEmbedding（Node2Vec、DeepWalk、EGES）；
    • U2I类，如DSSM、YouTube DNN、Sentence Bert；
      在这里插入图片描述

  • 模型类：模型类的模式是将用户和item分别映射到一个向量空间，

相关文章：

推荐系统[八]算法实践总结V1：淘宝逛逛and阿里飞猪个性化推荐：召回算法实践总结【冷启动召回、复购召回、用户行为召回等算法实战】

0.前言：召回排序流程策略算法简介 推荐可分为以下四个流程，分别是召回、粗排、精排以及重排： 召回是源头，在某种意义上决定着整个推荐的天花板；粗排是初筛，一般不会上复杂模型；精排是整个推荐环节的重中之重，在特征和模型上都会做的比较复杂；重排，一般是做打散或满足…...

编程日记 2023/2/21 2:53:36

适合初学者的超详细实用调试技巧（下）

我们日常写代码的时候，常常会遇到bug的情况，这个时候像我这样的初学者就会像无头苍蝇一样这里改改那里删删，调试的重要性也就显现出来，这篇文章接着上文来讲解。 上文地址：(8条消息) 适合初学者的超详细实用调试技巧&…...

编程日记 2023/2/21 2:52:30

C# String与StringBuilder 的区分

重点 1)它是比较的栈里面的值是否相等(值比较) 2)Equals它比较的是堆里面的值是否相等(引用地址值比较) 3)Object.ReferenceEquals(obj1,obj2)它是比较的是内存地址是否相等 问题描述： 今日提交代码时候，被检测工具发出修改建议。遂补充一下知识 1.什么…...

编程日记 2023/2/21 2:51:21

【麒麟】基于GPS北斗卫星技术的NTP网络时间服务器

【麒麟】基于GPS北斗卫星技术的NTP网络时间服务器 【麒麟】基于GPS北斗卫星技术的NTP网络时间服务器 麒麟系统NTP授时方案 设计思路： 在通用的麒麟服务器内部固定一块北斗卫星接收模块并引出卫星天线接口，卫星模块接收北斗卫星数据并解码输出时间数据&…...

编程日记 2023/2/21 2:50:13

“互联网+”下劳动关系认定的现状

1. 劳动关系的认定标准。依据目前我国法律的有关规定, 判定劳动关系存在两种情况:其一, 在有书面劳动合同的情况下, 这时应以书面合同作为认定标准;其二, 在没有书面合同的情况下, 则依据2005年劳社部的《关于确立劳动关系有关事项的通知》来认定, 其中第一条:“用人单位招用劳…...

编程日记 2023/2/21 2:49:04

LPWAN及高效弹性工业物联网核心技术方案

20多年前的一辆拖拉机就是一个纯机械的产品，里面可能并没有电子或者软件的构成；而随后随着软件的发展，拖拉机中嵌入了软件，它能控制发动机的功率及拖拉机防抱死系统；接下来，通过融入各种软件，拖…...

编程日记 2023/2/21 2:47:56

OPTIONS FMTSEARCH

FMTSEARCH 指定要检索的格式目录列表&#xff0c;语法如下&#xff1a;OPTIONS FMTSEARCH(catalog-specification-1<catalog-specification-2 … >);使用PROC FORMAT时可以定义格式目录&#xff0c;LIBRARYlibref或LIBRARYlibref.catalog。格式目录可以是libref或libref.…...

编程日记 2023/2/21 2:46:49

Python3 pip

Python3 pip pip 是 Python 包管理工具&#xff0c;该工具提供了对 Python 包的查找、下载、安装、卸载的功能。 软件包也可以在 https://pypi.org/ 中找到。 目前最新的 Python 版本已经预装了 pip。 注意&#xff1a;Python 2.7.9 或 Python 3.4 以上版本都自带 pip 工具…...

编程日记 2023/2/21 2:45:41

【2023-02-20】JS逆向之翼支付

提示&#xff1a;文章仅供参考&#xff0c;禁止用于非法途径 文章目录前言分析总结前言 真的好久没更了…… 提示&#xff1a;以下是本篇文章正文内容&#xff0c;下面案例可供参考 分析 进到网页&#xff0c;加载两个接口 applyLoginFactor 接口返回一个RSA公钥&#xff0…...

编程日记 2023/2/21 2:43:30

假如面试官问你Babel的原理该怎么回答

1. 什么是 Babel 简单地说&#xff0c;Babel 能够转译 ECMAScript 2015 的代码&#xff0c;使它在旧的浏览器或者环境中也能够运行。 // es2015 的 const 和 arrow function const add (a, b) > a b;// Babel 转译后 var add function add(a, b) {return a b; };Babel…...

编程日记 2023/2/21 2:42:21

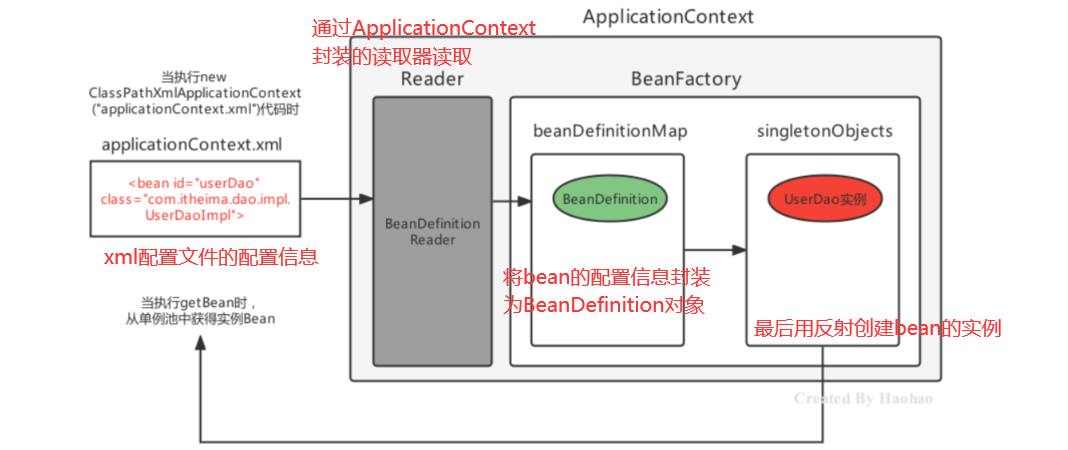
深入Spring底层透析Bean创建过程之拨云见日篇

目录前言一.BeanFactory快速入门1. BeanFactory创建Bean2. BeanFactory和ApplicationContext的关系3. 和ApplicationContext区别(高频问点)4. BeanFactory的继承体系5. ApplicationContext的继承体系二.Bean实例化的基本流程&#xff08;重点)前言 首先感谢您的阅览&#xff0…...

编程日记 2023/2/21 2:41:11

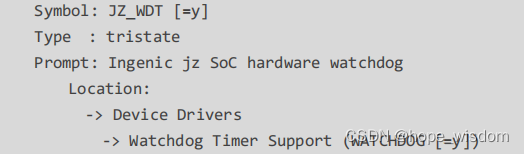
8 狗监控的封装

概述 为了保证嵌入式程序能够长时间稳定地运行，需要加入狗监控机制。狗监控的原理为：应用程序需要每隔一段时间来喂狗或保活，如果应用程序崩溃或者内核崩溃，导致长时间无法喂狗，则狗将超时，会自动重启系统。部分IPC芯片提供了硬件狗，对于没有硬件狗的，需要自行实现软件…...

编程日记 2023/2/21 2:40:02

基于卷积神经网络图像风格迁移系统的设计与实现（flask系统）

1.摘要 Leon Gatys 等人研发的深度神经网络使用神经的表达来分离任意图片的内容和风格&#xff0c;为生成艺术图片提供一个神经算法。本文基于Style Transfer算法&#xff0c;使用风格成本函数训练CNN&#xff0c;用卷积神经网络提取图像特征&#xff0c;依次提取内容图像的内…...

编程日记 2023/2/21 2:38:56

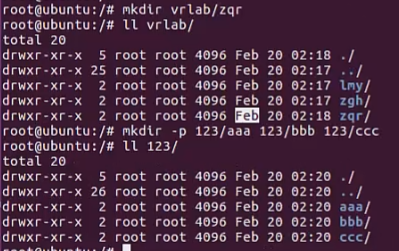
【1】linux命令每日分享——mkdir

大家好&#xff0c;这里是sdust-vrlab&#xff0c;Linux是一种免费使用和自由传播的类UNIX操作系统&#xff0c;Linux的基本思想有两点&#xff1a;一切都是文件&#xff1b;每个文件都有确定的用途&#xff1b;linux涉及到IT行业的方方面面&#xff0c;在我们日常的学习中&…...

编程日记 2023/2/21 2:37:49

实例2：树莓派GPIO控制外部LED灯闪烁

实例2&#xff1a;树莓派GPIO控制外部LED灯闪烁 实验目的 通过背景知识学习&#xff0c;了解四足机器人mini pupper搭载的微型控制计算机&#xff1a;树莓派。通过树莓派GPIO操作的学习&#xff0c;熟悉GPIO的读写控制。通过外部LED灯的亮灭控制&#xff0c;熟悉树莓派对外界…...

编程日记 2023/2/21 2:36:43

详解可变形注意力模块（Deformable Attention Module）

Deformable Attention&#xff08;可变形注意力&#xff09;首先在2020年10月初商汤研究院的《Deformable DETR: Deformable Transformers for End-to-End Object Detection》论文中提出&#xff0c;在2022CVPR中《Vision Transformer with Deformable Attention》提出应用了De…...

编程日记 2023/2/21 2:35:32

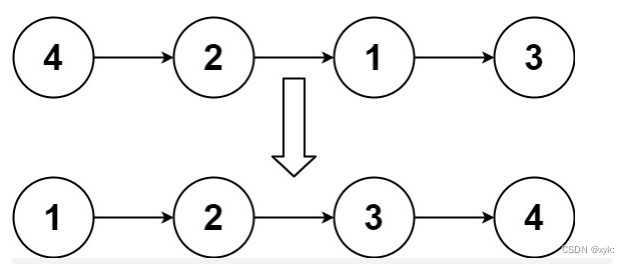
Java数据结构中链表分割及链表排序使用快速排序、归并排序、集合排序、迭代、递归，刷题的重点总结

本篇主要介绍在单链表进行分割&#xff0c;单链表进行分隔并使用快速排序、归并排序、集合排序、迭代、递归等方法的总结&#xff0c;愿各位大佬喜欢~~ 86. 分隔链表 - 力扣&#xff08;LeetCode&#xff09; 148. 排序链表 - 力扣&#xff08;LeetCode&#xff09; 目录 一…...

编程日记 2023/2/21 2:34:21

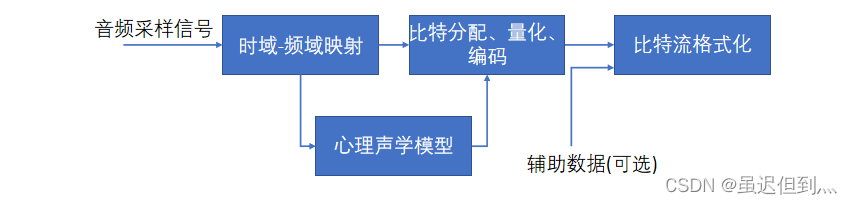
音视频基础之音频编码原理简介

一&#xff1a;隐蔽信号 数字音频信号如果不加压缩地直接进行传送&#xff0c;将会占用极大的带宽。例如&#xff0c;一套双声道数字音频若取样频率为44.1KHz&#xff0c;每样值按16bit量化&#xff0c;则其码率为&#xff1a; 244.1kHz16bit1.411Mbit/s 如此大的带宽将给信号…...

编程日记 2023/2/21 2:33:15

【Python--XML文件读写】XML文件读写详解

【Python–XML文件读写】XML文件读写详解 文章目录【Python--XML文件读写】XML文件读写详解1. 前言1.1 介绍1.2 用法2. xml文件内容形式3. xml文件读写3.1 项目框架3.1 写入操作&#xff08;创建&#xff09;&#xff08;create_xml.py&#xff09;3.2 读取操作&#xff08;解析…...

编程日记 2023/2/21 2:32:07

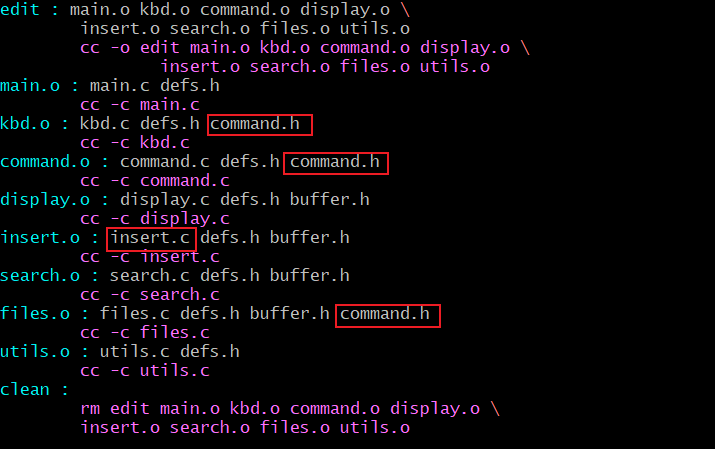
GNU make 中文手册 第一二章 概述与介绍

一、第一章&#xff1a;概述 准备知识 在开始我们关于 make 的讨论之前&#xff0c;首先需要明确一些基本概念&#xff1a; 编译&#xff1a;把高级语言书写的代码&#xff0c;转换为机器可识别的机器指令。编译高级语言后生成的指令虽然可被机器识别&#xff0c;但是还不能…...

编程日记 2023/2/21 2:30:59

生成xcframework

打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式&#xff0c;可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

编程新知 2025/10/5 2:30:38

大数据学习栈记——Neo4j的安装与使用

本文介绍图数据库Neofj的安装与使用&#xff0c;操作系统&#xff1a;Ubuntu24.04&#xff0c;Neofj版本&#xff1a;2025.04.0。 Apt安装 Neofj可以进行官网安装&#xff1a;Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

编程新知 2026/2/8 4:37:08

Cursor实现用excel数据填充word模版的方法

cursor主页&#xff1a;https://www.cursor.com/ 任务目标&#xff1a;把excel格式的数据里的单元格&#xff0c;按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例&#xff0c;…...

编程新知 2025/8/23 5:46:26

前端导出带有合并单元格的列表

// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

编程新知 2026/1/25 3:21:09

ServerTrust 并非唯一

NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

编程新知 2026/1/29 5:29:57

Linux-07 ubuntu 的 chrome 启动不了

文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了&#xff0c;报错如下四、启动不了&#xff0c;解决如下 总结 问题原因 在应用中可以看到chrome&#xff0c;但是打不开(说明&#xff1a;原来的ubuntu系统出问题了&#xff0c;这个是备用的硬盘&a…...

编程新知 2026/1/29 17:56:19

WEB3全栈开发——面试专业技能点P2智能合约开发（Solidity）

一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解&#xff0c;适合用作学习或写简历项目背景说明。 &#x1f9e0; 一、概念简介&#xff1a;Solidity 合约开发 Solidity 是一种专门为 以太坊&#xff08;Ethereum&#xff09;平台编写智能合约的高级编…...

编程新知 2026/1/27 9:33:09

Caliper 配置文件解析：fisco-bcos.json

config.yaml 文件 config.yaml 是 Caliper 的主配置文件，通常包含以下内容： test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

编程新知 2025/10/24 15:14:02

【FTP】ftp文件传输会丢包吗？批量几百个文件传输，有一些文件没有传输完整，如何解决？

FTP&#xff08;File Transfer Protocol&#xff09;本身是一个基于 TCP 的协议&#xff0c;理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况&#xff0c;主要原因包括&#xff1a; ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

编程新知 2025/8/17 3:31:21

02.运算符

目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&&#xff1a;逻辑与 ||&#xff1a;逻辑或 &#xff01;&#xff1a;逻辑非 短路求值 位运算符 按位与&&#xff1a; 按位或 | 按位取反~ …...

编程新知 2026/2/6 15:27:20