二叉树的层序遍历及完全二叉树的判断
文章目录
1.二叉树层序遍历
2.完全二叉树的判断
文章内容
1.二叉树层序遍历
二叉树的层序遍历需要一个队列来帮助实现。
我们在队列中存储的是节点的地址,所以我们要对队列结构体的数据域重定义,
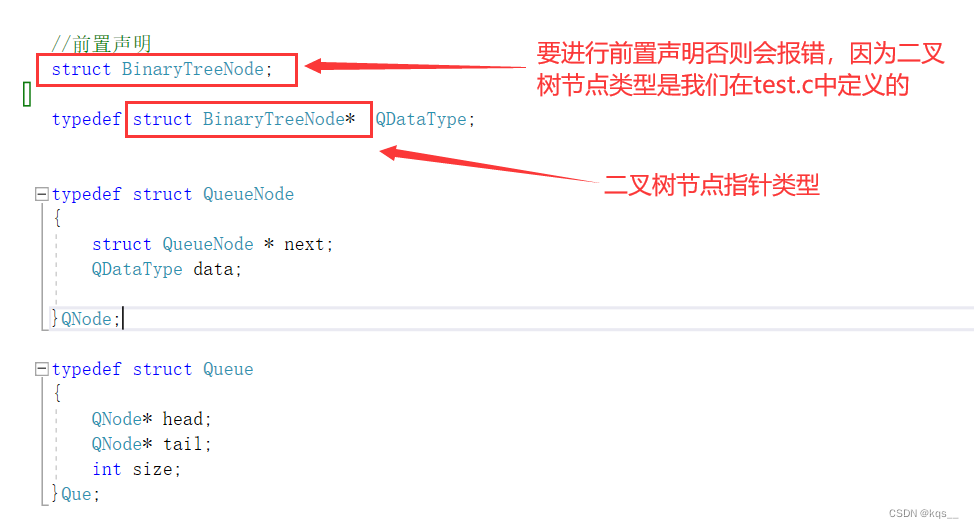
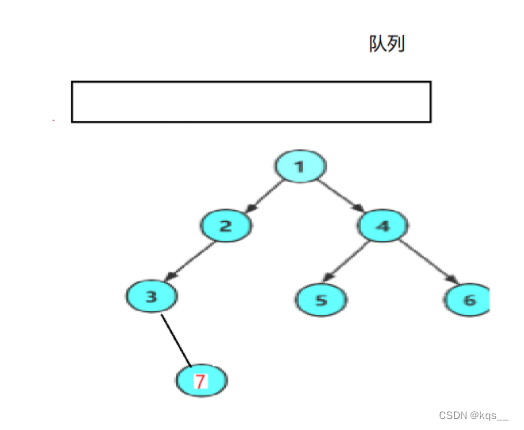
以上代码 从逻辑上来讲就是1入队,1出队,2(1的左孩子)入队,4(1的右孩子)入队,2出队......
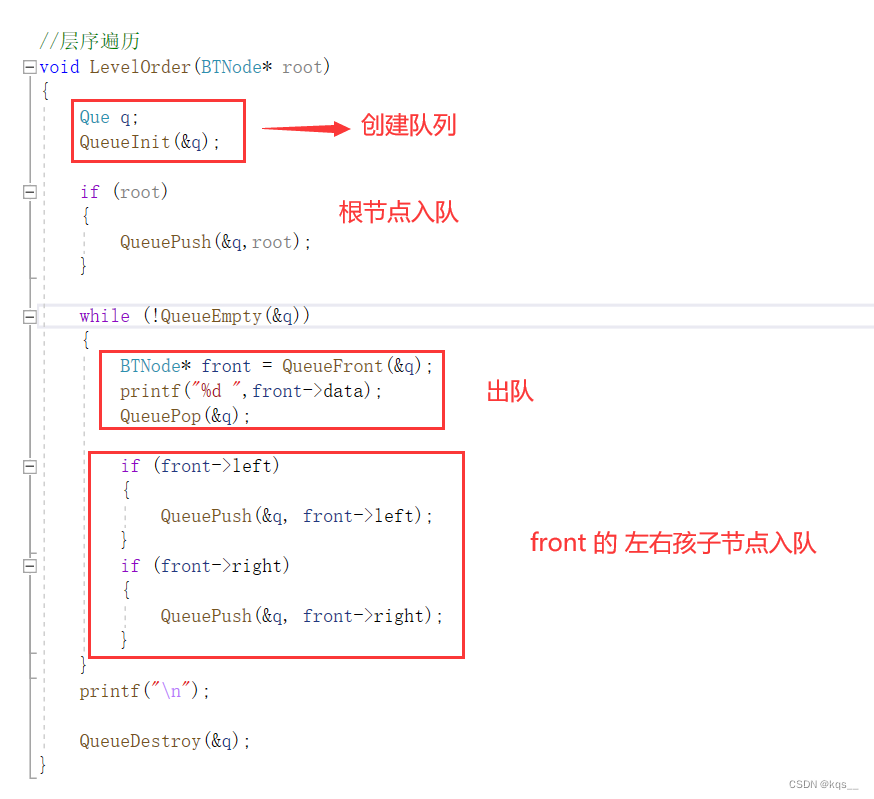
//层序遍历
void LevelOrder(BTNode* root)
{Que q;QueueInit(&q);if (root){QueuePush(&q,root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%d ",front->data);QueuePop(&q);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
2.完全二叉树的判断
完全二叉树的判断和二叉树的层序的思想差不多,都需要借助队列来实现。
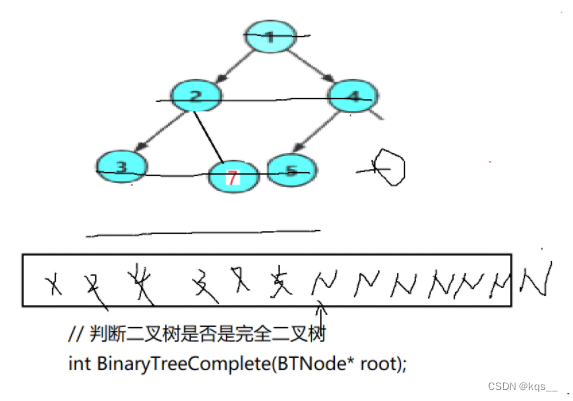
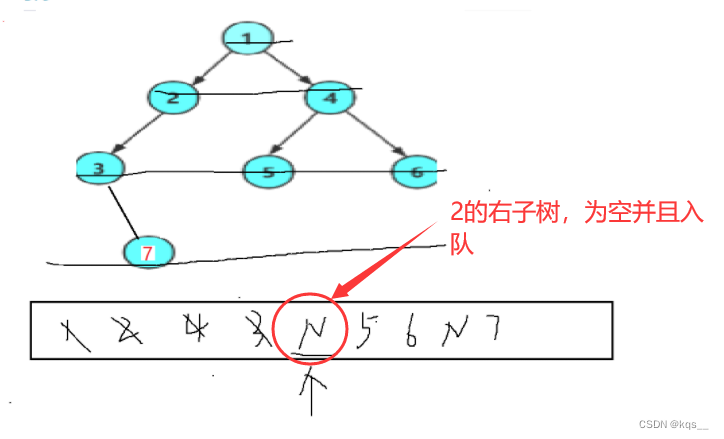

bool TreeComplete(BTNode* root)
{Que q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);// printf("%d ", front->data);QueuePop(&q);if (front) //front的左子树 右子树 不管为不为空都入队{QueuePush(&q, front->left);QueuePush(&q, front->right);}else{break;//当front 为空的时候,跳出循环开始判断是否为完全二叉树}}while (!QueueEmpty(root)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(root);return false;}}
// printf("\n");return true;
}相关文章:

二叉树的层序遍历及完全二叉树的判断
文章目录 1.二叉树层序遍历 2.完全二叉树的判断 文章内容 1.二叉树层序遍历 二叉树的层序遍历需要一个队列来帮助实现。 我们在队列中存储的是节点的地址,所以我们要对队列结构体的数据域重定义, 以上代码 从逻辑上来讲就是1入队,1出队&am…...
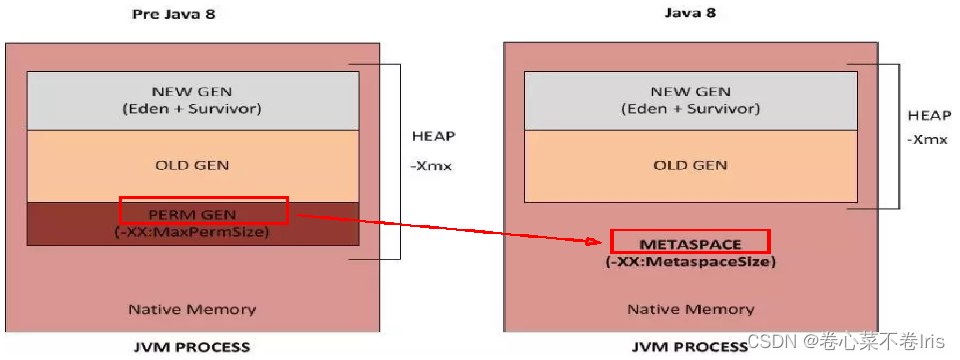
java八股文面试[JVM]——JVM内存结构
参考: JVM学习笔记(一)_卷心菜不卷Iris的博客-CSDN博客 JVM是运行在操作系统之上的,它与硬件没有直接的交互 JVM内存结构: 方法区:存储已被虚拟机加载的类元数据信息(元空间) 堆:存放对象实…...
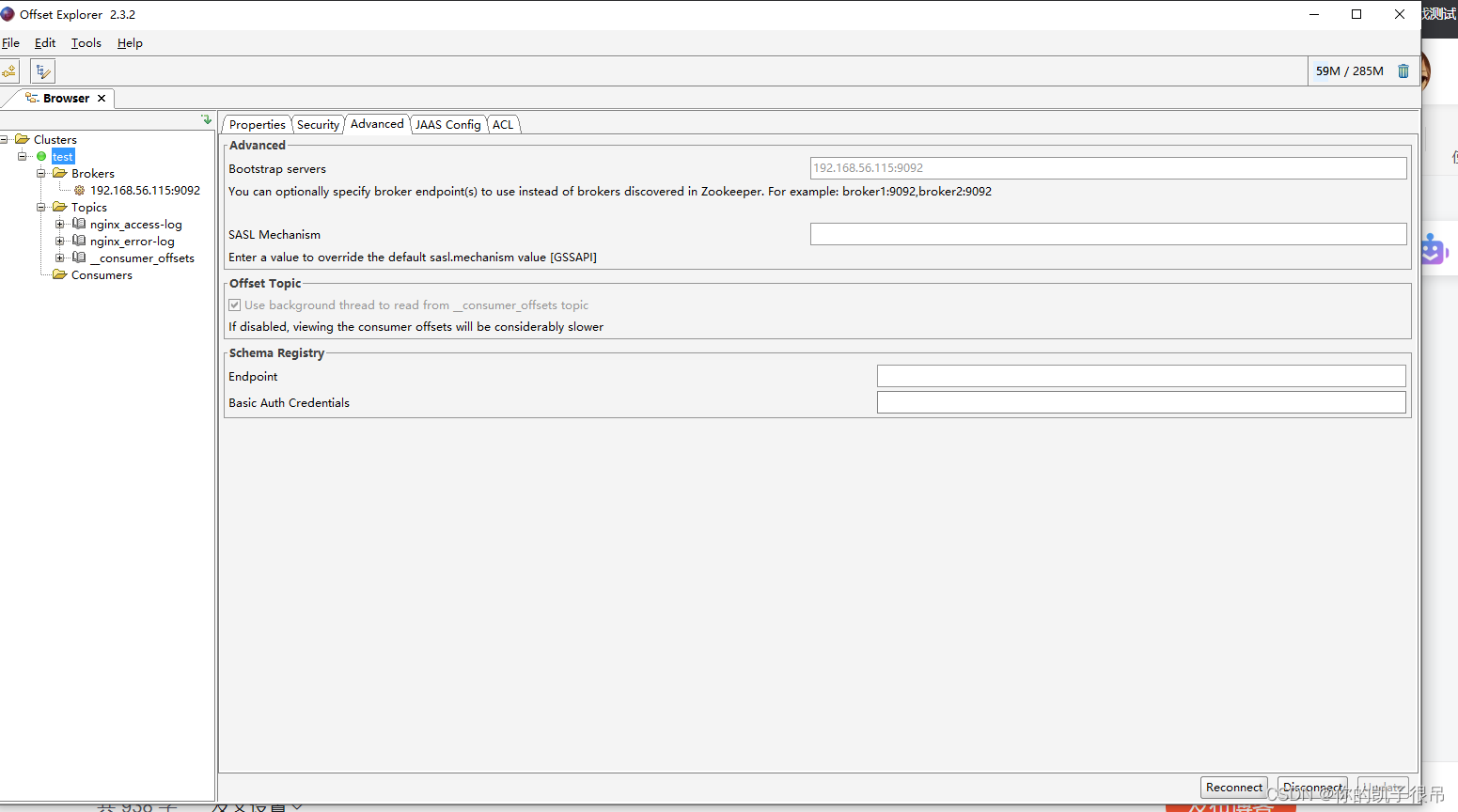
Kafka基本使用
查看Kafka的进程是否在运行 #命令行终端中运行如下命令 ps -ef | grep kafkafind / -iname kafka-server-start.shcd /usr/local/kafka/bin/#启动kafka ./kafka-server-start.sh -daemon /usr/local/kafka/config/server.propertiesKafka默认使用9092端口提供服务…...
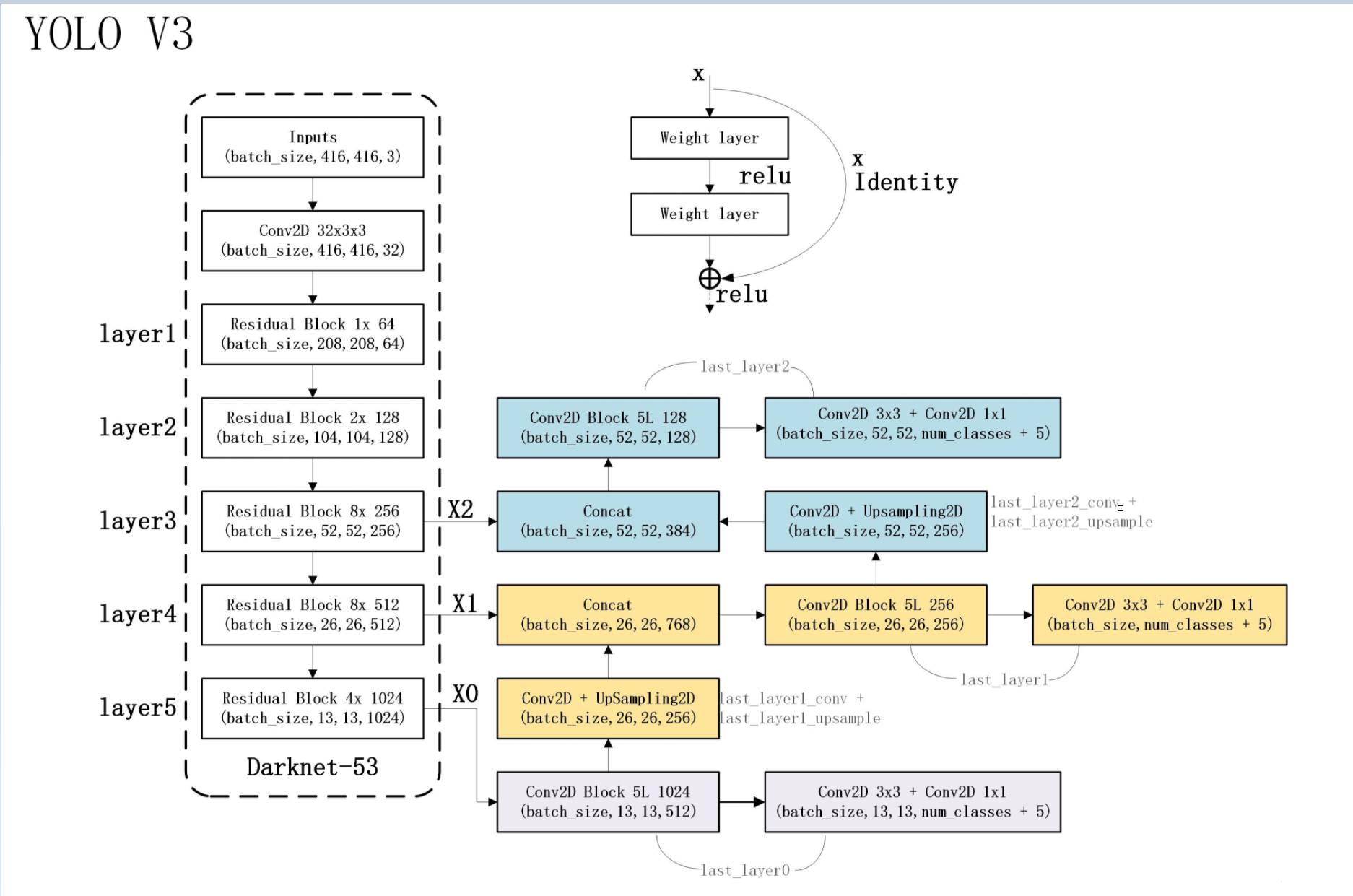
【目标检测】理论篇(2)YOLOv3网络构架及其代码实现
网络构架图: 代码实现: import math from collections import OrderedDictimport torch.nn as nn#---------------------------------------------------------------------# # 残差结构 # 利用一个1x1卷积下降通道数,然后利用一个3x3卷…...

k8s之工作负载、Deployment、DaemonSet、StatefulSet、Job、CronJob及GC
文章目录 1、工作负载1.1、定义1.2、分类 2、Deployment2.1、定义2.2、Deployment创建2.3、Deployment 更新机制2.3.1、比例缩放(Proportional Scaling)2.3.2、HPA(动态扩缩容)2.3.2.1、需要先安装metrics-server2.3.2.2、配置hpa…...
IDEA项目实践——Element UI概述
系列文章目录 IDEA项目实践——JavaWeb简介以及Servlet编程实战 IDEA项目实践——Spring当中的切面AOP IDEA项目实践——Spring框架简介,以及IOC注解 IDEA项目实践——动态SQL、关系映射、注解开发 IDEWA项目实践——mybatis的一些基本原理以及案例 文章目录 …...
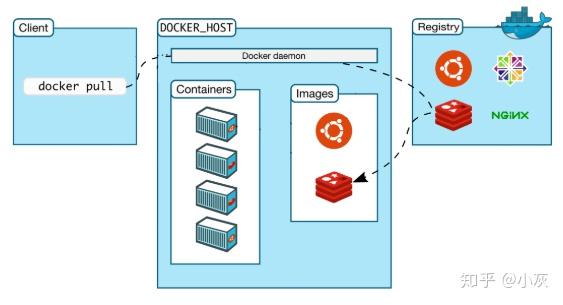
Docker 容器学习笔记
Docker 容器学习笔记 容器的由来 早先,虚拟机通过操作系统实现相互隔离,保证应用程序在运行时相互独立,避免相互干扰。但是操作系统又笨又重,耗费资源严重: 容器技术只隔离应用程序的运行时环境但容器之间共享同一个…...

Day03-vue基础
Day03-vue基础 一 列表渲染 v-for这个指令可以实现列表渲染 1 数组 <ul><!-- v-for遍历的时候,key必须赋唯一值第一个参数是数组元素,第二个参数是元素下标--><li v-for="(item,index) in [1,3,5,7]" :key="item">{{item}}--{{index}…...

RAC sid=‘*‘ 最好加上 v$system_parameter
实验结论:在RAC环境中,最好修改参数sid* 安全可靠,因为暂时未明确知道哪些参数是默认全局修改,什么参数是默认单节点修改的,* 靠谱,不容易出问题 在RAC环境中,修改全局参数scopespfile生效时&am…...

【位运算进阶之----左移(<<)】
今天我们来谈谈左移这件事。 ❤️简单来说,对一个数左移就是在其的二进制表达末尾添0。左移一位添一个0,结果就是乘以2;左移两位添两个0,结果就乘以2 ^ 2;左移n位添n个0,结果就是乘以2 ^ n,小心…...
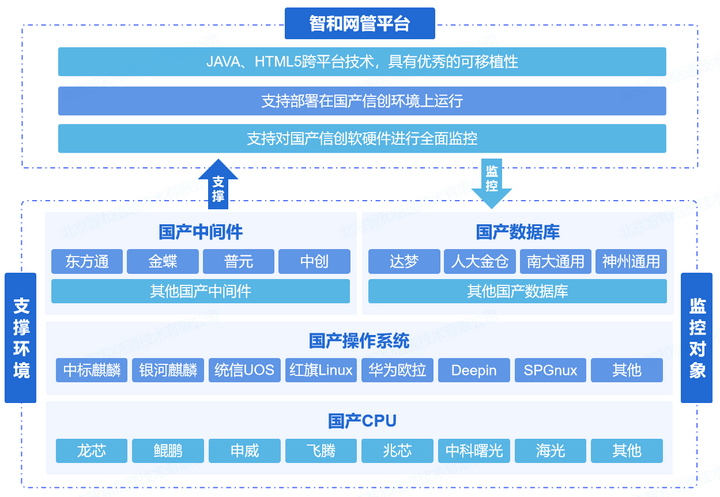
石油石化行业网络监控运维方案,全局态势感知,实时预警
石油石化行业是一个高科技密集型行业,投资巨大、人员众多,各产业价值链的关联度较高,大型石油石化企业实现了上中下游产业的一体化协同发展。随着工业4.0时代的来临,信息化和工业化融合,物联网、云计算等新技术的普及推…...

MyBatis 的关联关系配置 一对多,一对一,多对多 关系的映射处理
目录 一.关联关系配置的好处 二. 导入数据库表: 三. 一对多关系:-- 一个订单对应多个订单项 四.一对一关系:---一个订单项对应一个订单 五.多对多关系(两个一对多) 一.关联关系配置的好处 MyBatis是一…...

Diffusion Models for Image Restoration and Enhancement – A Comprehensive Survey
图像恢复与增强的扩散模型综述 论文链接:https://arxiv.org/abs/2308.09388 项目地址:https://github.com/lixinustc/Awesome-diffusion-model-for-image-processing/ Abstract 图像恢复(IR)一直是低水平视觉领域不可或缺的一项具有挑战性的任务&…...
Springboot开发所遇问题(持续更新)
SpringBoot特征: 1. SpringBoot Starter:他将常用的依赖分组进行了整合,将其合并到一个依赖中,这样就可以一次性添加到项目的Maven或Gradle构建中。 2,使编码变得简单,SpringBoot采用 JavaConfig的方式对Spring进行配置…...
智能电视与win10电脑后续无法实现DLNA屏幕共享
问题背景: 我用的是TCL电视,但是并不是最新,打开的方式是U盘->电脑,各位看自己情况,很多问题都大概率是智能电视问题。 情景假设: 假设你已经完成原先智能电视该有的步骤,通过DLNA…...

如何可以管理监督员工工作微信?
自从微信管理系统研发上线之后,为了各企业带来了福音。 很多用户企业都是这样评论微信管理系统的:员工的所有微信聊天记录后台都可以清楚明了的看到,聊天记录都是永久保存的,不担心员工在手机上把聊天记录删除,杜绝员…...

【Django】如何转化已有的数据表到Django模型--20230823
初步生成model.py $ python manage.py inspectdb $ python manage.py inspectdb > models.py python manage.py inspectdb # This is an auto-generated Django model module. # Youll have to do the following manually to clean this up: # * Rearrange models order…...

【C语言】喝汽水问题
大家好!今天我们来学习C语言中的喝汽水问题! 目录 1. 题目内容: 2. 思路分析 2.1 方法一 2.2 方法二 2.3 方法三 3. 代码实现 3.1 方法一 3.2 方法二 3.3 方法三 1. 题目内容 喝汽水,1瓶汽水1元,2个空瓶可以…...
项目进度管理(4-2)关键链法和关键路径法的区别和联系
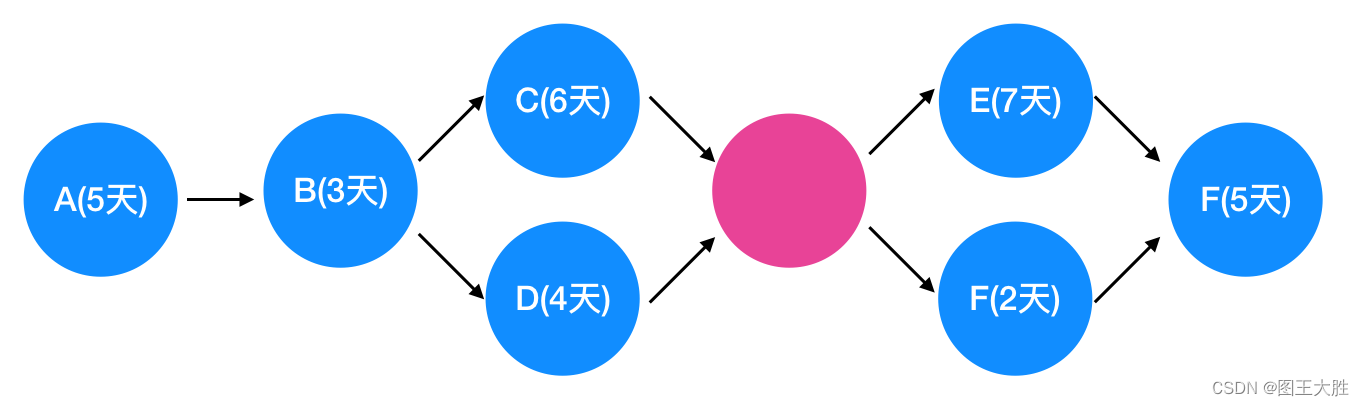
1 关键链法和关键路径法的主要区别 1.1 关键链法和关键路径法的关注焦点不同 关键路径法(CPM):关注项目中最长的路径,也就是所需时间最长的路径,这被称为关键路径。关键路径决定了项目的最早完成时间。关键链法&…...
基于Java+SpringBoot+Vue前后端分离医院后台管理系统设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
