当前位置： 首页 > news >正文

R语言画样本不均衡组的箱线图

news 2026/2/7 13:55:52 
# 导入 ggplot2 包
library(ggplot2)# 示例数据框，包含数值数据和分组信息
data <- data.frame(Group = c(rep("Group A",10), rep("Group B",15),rep("Group C",20)),Value = c(rnorm(10, mean = 10, sd = 2),rnorm(15, mean = 15, sd = 2),rnorm(20, mean = 20, sd = 2))
)# 使用 ggplot2 绘制箱线图，同时显示每个数据点
ggplot(data, aes(x = Group, y = Value, fill = Group)) +geom_boxplot(outlier.shape = NA) +  # 不显示异常值geom_jitter(width = 0.2, alpha = 0.7) +  # 绘制数据点，width控制点的分布宽度，alpha控制透明度labs(title = "Box Plot with Unequal Group Sizes and Data Points",x = "Group",y = "Value") +theme_minimal()  # 使用简洁的主题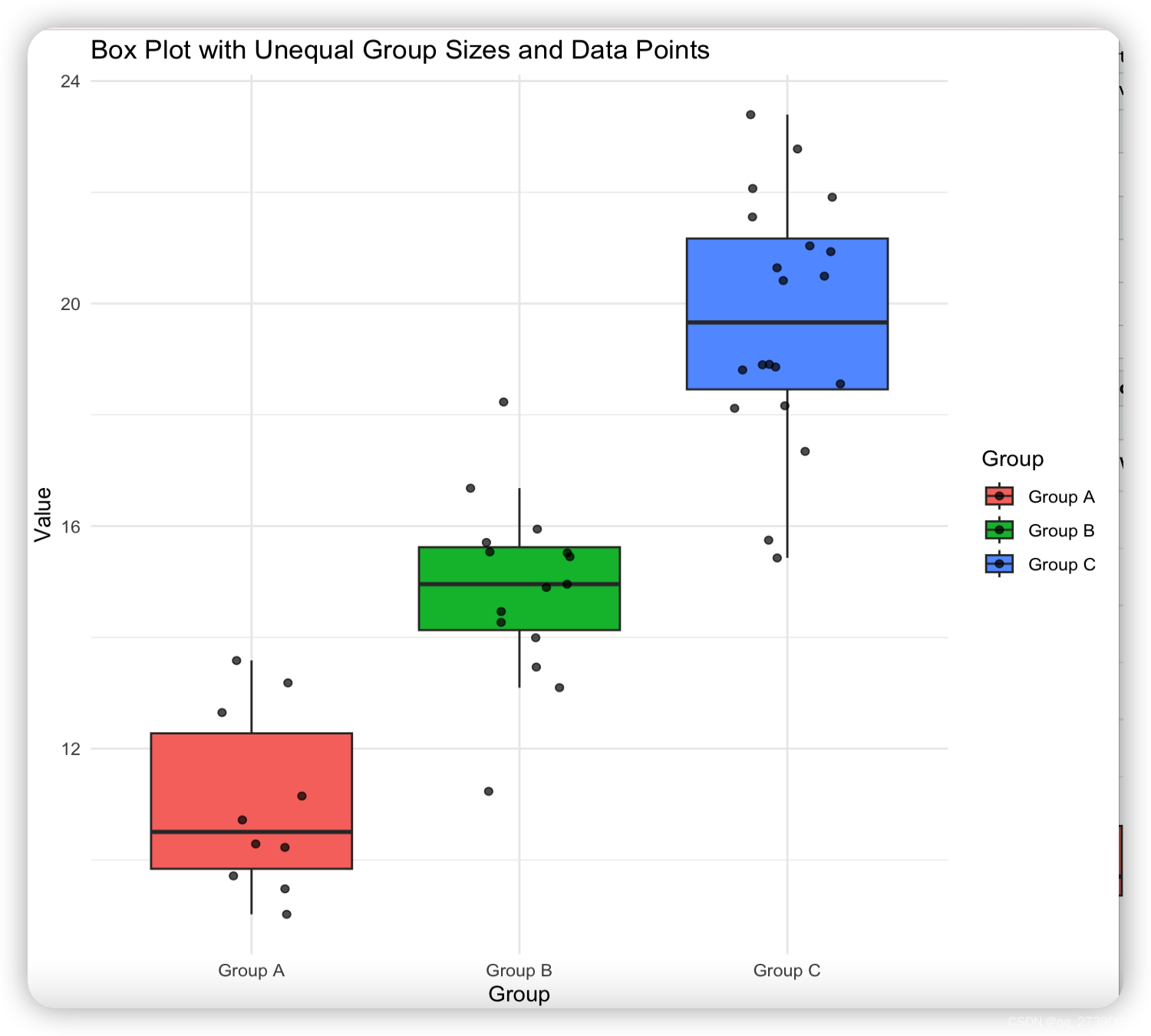

 

相关文章：

R语言画样本不均衡组的箱线图

# 导入 ggplot2 包 library(ggplot2)# 示例数据框&#xff0c;包含数值数据和分组信息 data <- data.frame(Group c(rep("Group A",10), rep("Group B",15),rep("Group C",20)),Value c(rnorm(10, mean 10, sd 2),rnorm(15, mean 15, sd…...

编程日记 2023/8/27 4:54:46

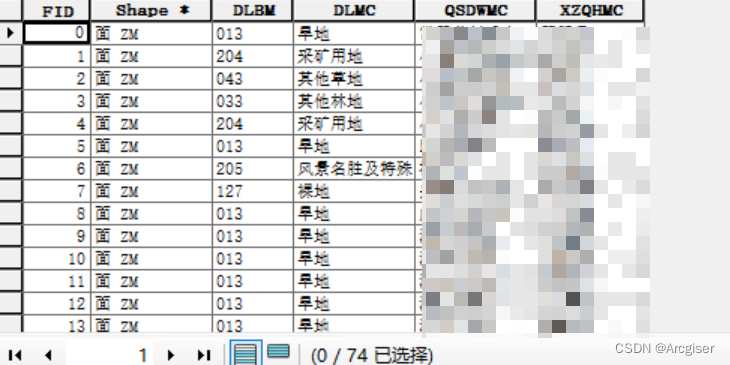
ArcGIS学习总结（19）——要素转点与空间连接（属性表字段映射）

1.在新创建的面矢量数据的属性表中没有对应的字段信息&#xff0c;为了能够和有属性信息的数据进行匹配&#xff0c;使其具有对应字段的信息。 2.需要匹配的矢量文件属性表信息。 3.对新创建的矢量文件执行要素转点&#xff1a;数据管理工具→要素→要素转点。 4.选择分析工…...

编程日记 2023/8/27 4:53:43

【每日一题Day306】LC228汇总区间 | 双指针

汇总区间【LC228】 给定一个 无重复元素 的 有序 整数数组 nums 。 返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说&#xff0c;nums 的每个元素都恰好被某个区间范围所覆盖&#xff0c;并且不存在属于某个范围但不属于 nums 的数字 x 。 列表中的每个区间范…...

编程日记 2023/8/27 4:52:42

vue中实现echarts三维散点图

需要安装 echarts 同时引入 echarts-gl 我安装的版本&#xff1a; "echarts": "^5.3.2", "echarts-gl": "^2.0.9", import Vue from "vue"; import * as echarts from "echarts"; Vue.prototype.$echarts echa…...

编程日记 2023/8/27 4:51:40

多头自注意力机制的代码实现

文章目录 1、自注意力机制2、多头注意力机制 transformer的整体结构&#xff1a; 1、自注意力机制 自注意力机制如下&#xff1a; 计算过程&#xff1a; 代码如下&#xff1a; class ScaledDotProductAttention(nn.Module):def __init__(self, embed_dim, key_size, value_…...

编程日记 2023/8/27 4:50:39

抽象工厂模式

目录 了解抽象工厂模式前的前置知识 什么是抽象工厂模式&#xff1f; 为什么要提出抽象工厂模式&#xff1f; 抽象工厂模式中的四大角色&#xff1f; 抽象工厂模式的优缺点&#xff1f; 抽象工厂模式的适用场景&#xff1f; 了解抽象工厂模式前的前置知识 在讲抽象工厂模式…...

编程日记 2023/8/27 4:49:37

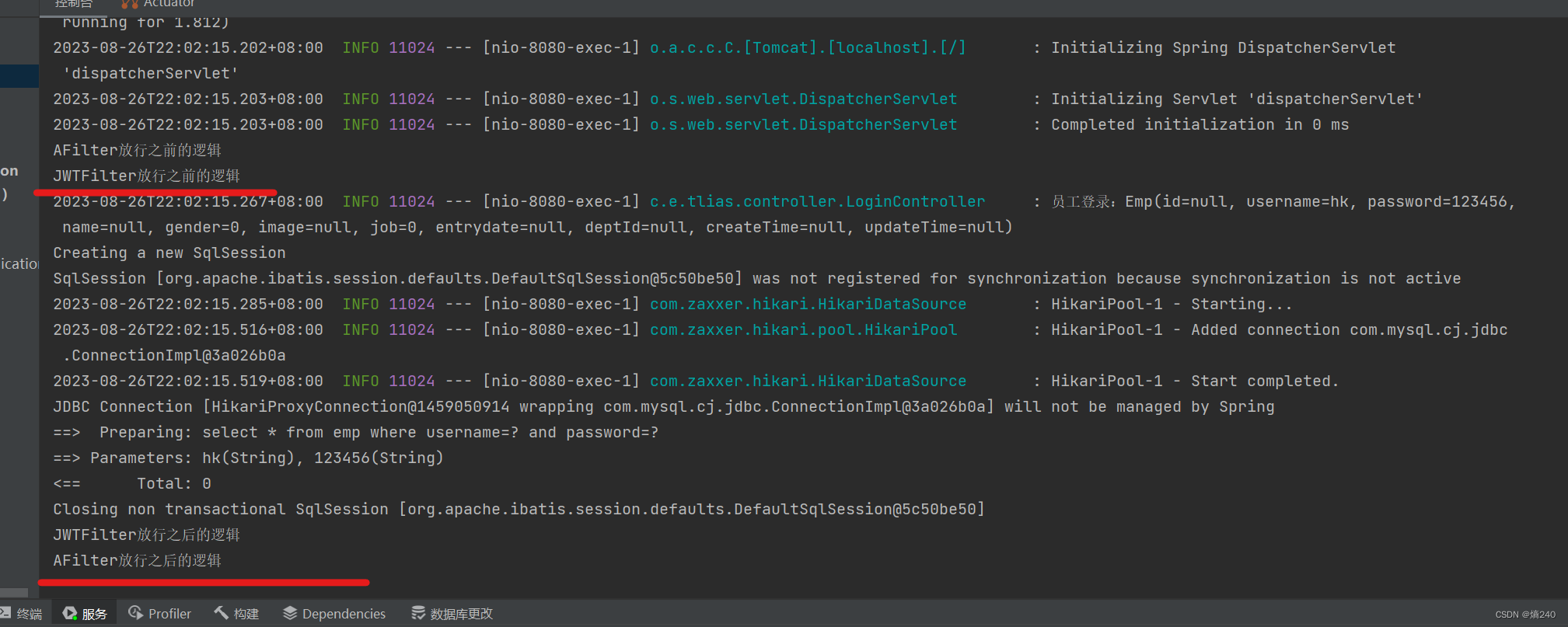
登录校验-Filter-详解

目录 执行流程 拦截路径 过滤器链 小结 执行流程 过滤器Filter拦截到请求之后&#xff0c;首先执行方放行之前的逻辑&#xff0c;然后执行放行操作&#xff08;doFilter&#xff09;&#xff0c;然后会访问对应的Web资源&#xff08;对应的Controller类&#xff09;&#…...

编程日记 2023/8/27 4:48:36

堆栈方法区笔记记录

成员变量分两种: 1)实例变量:没有static修饰&#xff0c;属于对象&#xff0c;存储在堆中&#xff0c;有几个对象就有几份&#xff0c;通过对象点来访问 2)静态变量:由static修饰&#xff0c;属于类&#xff0c;存储在方法区中&#xff0c;只有一份&#xff0c;通过类名点来访…...

编程日记 2023/8/27 4:47:35

新版微信小程序获取用户手机号

小程序手机号验证组件有两种 手机号快速验证组件 //原生写法 <button open-type"getPhoneNumber" bindgetphonenumber"getPhoneNumber"></button>Page({getPhoneNumber (e) {console.log(e.detail.code)} })uniapp写法 <button open-type…...

编程日记 2023/8/27 4:46:34

CSS实践 —— 悬浮盒子阴影加上移效果

悬浮盒子阴影加上移效果 代码 代码 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><title>Title</title><style>body{background-color: #f5f5f5;}.shadow {width: 100px;height: 100px;margin:…...

编程日记 2023/8/27 4:45:33

安全测试基础知识

软件安全测试是评估和测试系统以发现系统及其数据的安全风险和漏洞的过程。没有通用术语&#xff0c;但出于我们的目的&#xff0c;我们将评估定义为分析和发现漏洞&#xff0c;而不尝试实际利用这些漏洞。我们将测试定义为发现和尝试利用漏洞。 安全测试通常根据要测试的漏洞…...

编程日记 2023/8/27 4:44:32

列表首屏毫秒级加载与自动滚动定位方案

引用自 摸鱼wiki 场景 <template><div ref"commentsRef"><divv-for"comment in displayComments":key"comment.id":data-cell-id"comment.id"class"card">{{ comment.data }}</div></div> &…...

编程日记 2023/8/27 4:43:30

小区物业业主管理信息系统设计的设计与实现(论文+源码)_kaic

摘 要 随着互联网的发展&#xff0c;网络技术的发展变得极其重要&#xff0c;所以依靠计算机处理业务成为了一种社会普遍的现状。管理方式也自然而然的向着现代化技术方向而改变&#xff0c;所以纯人工管理方式在越来越完善的现代化管理技术的比较之下也就显得过于繁琐&#x…...

编程日记 2023/8/27 4:42:29

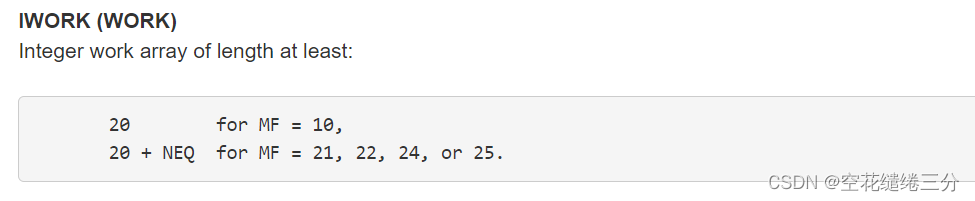
Fortran 微分方程求解 --ODEPACK

最近涉及到使用Fortran对微分方程求解&#xff0c;我们知道MATLAB已有内置的函数&#xff0c;比如ode家族&#xff0c;ode15s&#xff0c;对应着不同的求解办法。通过查看odepack的官方文档&#xff0c;我尝试使用了dlsode求解刚性和非刚性常微分方程组。 首先是github网址&am…...

编程日记 2023/8/27 4:41:27

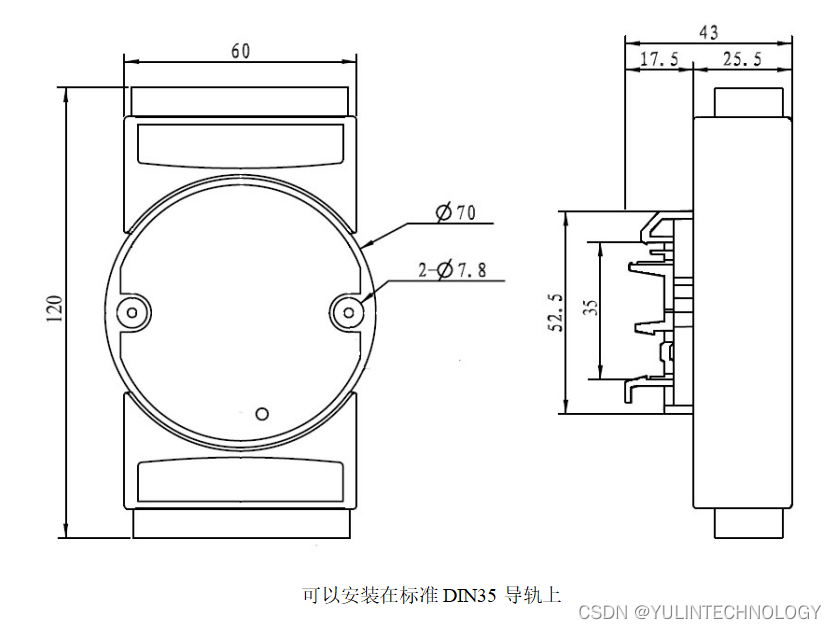
8路光栅尺磁栅尺编码器或16路高速DI脉冲信号转Modbus TCP网络模块 YL99-RJ45

特点&#xff1a; ● 光栅尺磁栅尺解码转换成标准Modbus TCP协议 ● 高速光栅尺磁栅尺4倍频计数&#xff0c;频率可达5MHz ● 模块可以输出5V的电源给光栅尺或传感器供电 ● 支持8个光栅尺同时计数&#xff0c;可识别正反转 ● 可以设置作为16路独立DI高速计数器 ● 可网…...

编程日记 2023/8/27 4:40:26

【Python】函数

None类型 思考&#xff1a;若函数没有使用return语句返回数据&#xff0c;那么函数有返回值吗&#xff1f; 答&#xff1a;实际上是有的&#xff0c;Python中有一个特殊的字面量None&#xff0c;其类型是<class ‘NoneType’>&#xff0c;无返回值的函数&#xff0c;实…...

编程日记 2023/8/27 4:39:24

centos安装MySQL 解压版完整教程（按步骤傻瓜式安装

一、卸载系统自带的 Mariadb 查看&#xff1a; rpm -qa|grep mariadb 卸载&#xff1a; rpm -e --nodeps mariadb-libs-5.5.68-1.el7.x86_64 二、卸载 etc 目录下的 my.cnf 文件 rm -rf /etc/my.cnf 三、检查MySQL是否存在 有则先删除 #卸载mysql服务以及删除所有mysql目录 #没…...

编程日记 2023/8/27 4:38:21

【后端速成 Vue】第一个 Vue 程序

1、为什么要学习 Vue&#xff1f; 为什么使用 Vue? 回想之前&#xff0c;前后端交互的时候&#xff0c;前端收到后端响应的数据&#xff0c;接着将数据渲染到页面上&#xff0c;之前使用的是 JavaScript 或者 基于 JavaScript 的 Jquery&#xff0c;但是这两个用起来还是不太…...

编程日记 2023/8/27 4:37:20

Macbook pro M1 安装Ubuntu教程

先讲下心路历程 由于版主最近刚切换到Mac&#xff0c;所以在安装的时候一上手就选择了virutalbox&#xff0c;结果报错“The installer has detected an unsupported architecture. VirtualBox only runs on the amd64 architecture.” 后来去Reddit论坛上一看&#xff0c;才知…...

编程日记 2023/8/27 4:36:17

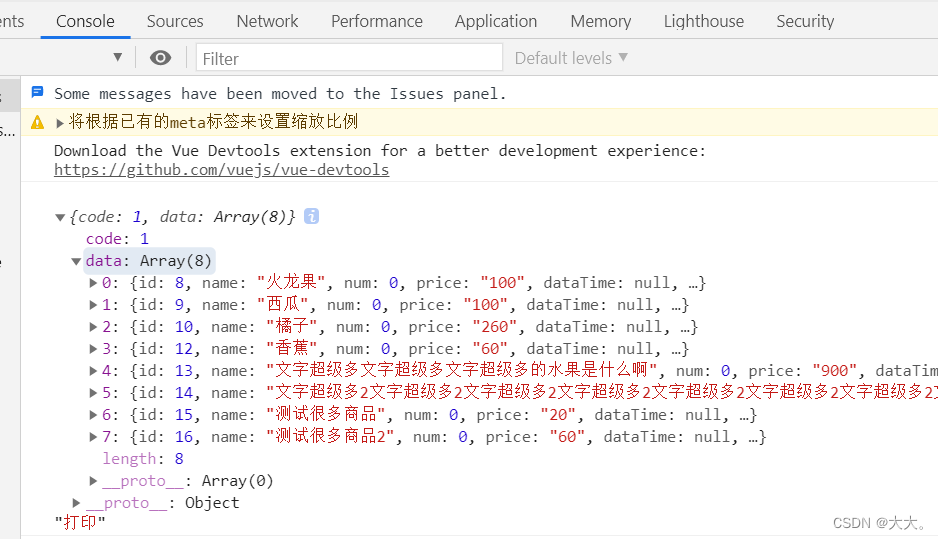
前端console.log打印内容与后端请求返回数据不一致

后端传值num0 前端打印num1 ,如图&#xff0c;console.log后台显示的数据与展开后不一致 造成该问题原因是深拷贝与浅拷贝的问题。 var obj JSON.parse(JSON.stringify(res)) 修改后打印 正常...

编程日记 2023/8/27 4:35:16

后进先出（LIFO）详解

LIFO 是 Last In, First Out 的缩写&#xff0c;中文译为后进先出。这是一种数据结构的工作原则&#xff0c;类似于一摞盘子或一叠书本&#xff1a; 最后放进去的元素最先出来 -想象往筒状容器里放盘子&#xff1a; &#xff08;1&#xff09;你放进的最后一个盘子&#xff08…...

编程新知 2026/2/5 15:43:28

Python爬虫实战：研究MechanicalSoup库相关技术

一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库，专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力，提供了直观的 API，让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

编程新知 2025/10/10 18:13:55

Lombok 的 @Data 注解失效，未生成 getter/setter 方法引发的HTTP 406 错误

HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误&#xff0c;它们的含义、原因和解决方法都有显著区别。以下是详细对比&#xff1a; 1. HTTP 406 (Not Acceptable) 含义&#xff1a; 客户端请求的内容类型与服务器支持的内容类型不匹…...

编程新知 2026/2/1 20:49:03

Leetcode 3576. Transform Array to All Equal Elements

Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接&#xff1a;3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到&#xf…...

编程新知 2025/9/17 7:25:07

linux 错误码总结

1，错误码的概念与作用 在Linux系统中，错误码是系统调用或库函数在执行失败时返回的特定数值，用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递，errno由操作系统维护，保存最近一次发生的错误信息。值得注意的是，errno的值在每次系统调用或函数调用失败时…...

编程新知 2025/9/16 22:48:47

Java面试专项一-准备篇

一、企业简历筛选规则 一般企业的简历筛选流程&#xff1a;首先由HR先筛选一部分简历后&#xff0c;在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如&#xff1a;Boss直聘&#xff08;招聘方平台&#xff09; 直接按照条件进行筛选 例如&#xff1a…...

编程新知 2026/1/26 19:10:48

PAN/FPN

import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

编程新知 2025/10/20 4:39:36

深度解析：etcd 在 Milvus 向量数据库中的关键作用

目录 &#x1f680; 深度解析&#xff1a;etcd 在 Milvus 向量数据库中的关键作用 &#x1f4a1; 什么是 etcd&#xff1f; &#x1f9e0; Milvus 架构简介 &#x1f4e6; etcd 在 Milvus 中的核心作用 &#x1f527; 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

编程新知 2025/10/31 3:16:51

深度解析云存储：概念、架构与应用实践

在数据爆炸式增长的时代&#xff0c;传统本地存储因容量限制、管理复杂等问题&#xff0c;已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性&#xff0c;成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理&#xff0c;云存储正重塑数据存储与…...

编程新知 2025/10/30 6:08:18

基于Python的气象数据分析及可视化研究

目录 一.&#x1f981;前言二.&#x1f981;开源代码与组件使用情况说明三.&#x1f981;核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.&#x1f981;演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...

编程新知 2026/2/6 1:10:23