【考研数学】线性代数第四章 —— 线性方程组(1,基本概念 | 基本定理 | 解的结构)
文章目录
- 引言
- 一、线性方程组的基本概念与表达形式
- 二、线性方程组解的基本定理
- 三、线性方程组解的结构
- 写在最后
引言
继向量的学习后,一鼓作气,把线性方程组也解决了去。O.O
一、线性方程组的基本概念与表达形式
方程组
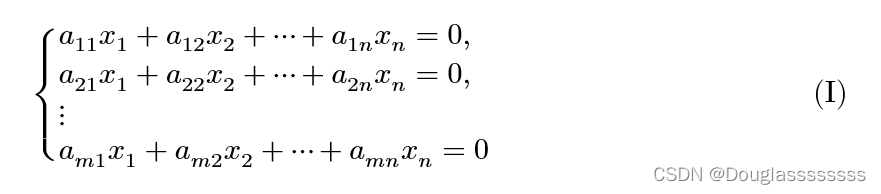
称为 n n n 元齐次线性方程组。
方程组
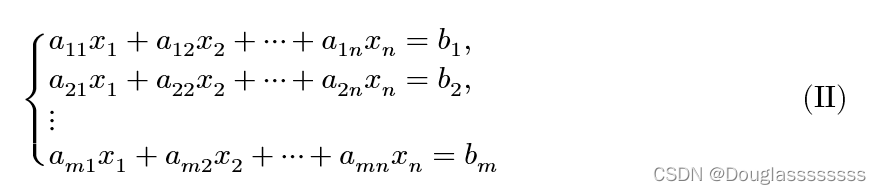
称为 n n n 元非齐次线性方程组。
方程组(I)又称为方程组(II)对应的齐次线性方程组或导出方程组。
方程组(I)和方程组(II)分别称为齐次线性方程组和非齐次线性方程组的基本形式。
令 α 1 = ( a 11 , a 21 , … , a m 1 ) T , α 2 = ( a 12 , a 22 , … , a m 2 ) T , … , α n = ( a 1 n , a 2 n , … , a m n ) T , b = ( b 1 , b 2 , … , b m ) T \alpha_1=(a_{11},a_{21},\dots,a_{m1})^T,\alpha_2=(a_{12},a_{22},\dots,a_{m2})^T,\dots,\alpha_n=(a_{1n},a_{2n},\dots,a_{mn})^T,b=(b_{1},b_{2},\dots,b_{m})^T α1=(a11,a21,…,am1)T,α2=(a12,a22,…,am2)T,…,αn=(a1n,a2n,…,amn)T,b=(b1,b2,…,bm)T ,则方程组(I)(II)可表示为如下向量形式: x 1 α 1 + x 2 α 2 + ⋯ + x n α n = 0 ( 1.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=0 (1.1) x1α1+x2α2+⋯+xnαn=0(1.1) x 1 α 1 + x 2 α 2 + ⋯ + x n α n = b ( 2.1 ) x_1\alpha_1+x_2\alpha_2+\dots+x_n\alpha_n=b (2.1) x1α1+x2α2+⋯+xnαn=b(2.1)
令 X = ( x 1 , x 2 , … , x n ) T X=(x_1,x_2,\dots,x_n)^T X=(x1,x2,…,xn)T ,矩阵 A = [ α 1 , α 2 , … , α n ] A=[\alpha_1,\alpha_2,\dots,\alpha_n] A=[α1,α2,…,αn] ,即

则方程组(I)(II)可表示为如下矩阵形式: A X = 0 ( 1.2 ) AX=0(1.2) AX=0(1.2) A X = b ( 2.2 ) AX=b(2.2) AX=b(2.2)
二、线性方程组解的基本定理
其实就是前面我们在学向量时就已经总结过的,矩阵、向量和线性方程组解的关系,传送门。
- 齐次方程组只有零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性无关 ⇔ \Leftrightarrow ⇔ r ( A ) = n . r(A)=n. r(A)=n.
- 齐次方程组有非零解 ⇔ \Leftrightarrow ⇔ 向量组 α 1 , α 2 , … , α n \pmb{\alpha_1,\alpha_2,\dots,\alpha_n} α1,α2,…,αn 线性相关 ⇔ \Leftrightarrow ⇔ r ( A ) < n . r(A)<n. r(A)<n.
特别地,如果系数矩阵 A A A 为 n n n 阶方阵,还有以下结论:
- 齐次方程组只有零解 ⇔ \Leftrightarrow ⇔ ∣ A ∣ ≠ 0. |A| \ne 0. ∣A∣=0.
- 齐次方程组有非零解 ⇔ \Leftrightarrow ⇔ ∣ A ∣ = 0. |A| = 0. ∣A∣=0.
对于非齐次方程组解的情况,我们可对有解的情况进一步讨论。
- 非齐次方程组有解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) = r ( A ) . r(\overline{A})=r(A). r(A)=r(A).
- 非齐次方程组有唯一解 ⇔ \Leftrightarrow ⇔ r ( A ) = n . r(A)=n. r(A)=n.
- 非齐次方程组有无数解 ⇔ \Leftrightarrow ⇔ r ( A ) < n . r(A)<n. r(A)<n.
- 非齐次方程组无解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
特别地,如果系数矩阵 A A A 为 n n n 阶方阵,还有以下结论:
- 非齐次方程组有解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) = r ( A ) . r(\overline{A})=r(A). r(A)=r(A).
- 非齐次方程组有唯一解 ⇔ \Leftrightarrow ⇔ ∣ A ∣ ≠ 0. |A| \ne 0. ∣A∣=0.
- 非齐次方程组有无数解 ⇔ \Leftrightarrow ⇔ ∣ A ∣ = 0. |A|=0. ∣A∣=0.
- 非齐次方程组无解 ⇔ \Leftrightarrow ⇔ r ( A ‾ ) = r ( A ) + 1. r(\overline{A})=r(A)+1. r(A)=r(A)+1.
在学向量时就已经讨论了矩阵、向量和方程组解的关系的话,现在来学就会非常轻松。
对于系数矩阵是方阵的方程组,无非就是将行列式和秩联系了起来。如果矩阵的秩那一部分学得到位,也不是什么难点。因此如果要记忆就记忆秩的关系就好,行列式的结论自然能想到。
三、线性方程组解的结构
- 设 X 1 , X 2 , … , X s \pmb{X_1,X_2,\dots,X_s} X1,X2,…,Xs 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的一组解,则 k 1 X 1 + k 2 X 2 + ⋯ + k s X s k_1X_1+k_2X_2+\dots +k_sX_s k1X1+k2X2+⋯+ksXs 也为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的解,其中 k 1 , k 2 , … , k s k_1,k_2,\dots,k_s k1,k2,…,ks 为任意常数。
- 设 η 0 \pmb{\eta_0} η0 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的一个解, X 1 , X 2 , … , X s \pmb{X_1,X_2,\dots,X_s} X1,X2,…,Xs 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的一组解,则 k 1 X 1 + k 2 X 2 + ⋯ + k s X s + η 0 k_1X_1+k_2X_2+\dots +k_sX_s+\pmb{\eta_0} k1X1+k2X2+⋯+ksXs+η0 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的解。
- 设 η 1 , η 2 \pmb{\eta_1,\eta_2} η1,η2 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的两个解,则 η 1 − η 2 \pmb{\eta_1-\eta_2} η1−η2 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的解。
- 设 X 1 , X 2 , … , X s \pmb{X_1,X_2,\dots,X_s} X1,X2,…,Xs 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的一组解,若 k 1 X 1 + k 2 X 2 + ⋯ + k s X s k_1X_1+k_2X_2+\dots +k_sX_s k1X1+k2X2+⋯+ksXs 也为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的解的充要条件是 k 1 + k 2 + ⋯ + k s = 1. k_1+k_2+\dots+k_s=1. k1+k2+⋯+ks=1.
- 设 X 1 , X 2 , … , X s \pmb{X_1,X_2,\dots,X_s} X1,X2,…,Xs 为非齐次线性方程组 A X = b \pmb{AX=b} AX=b 的一组解,若 k 1 X 1 + k 2 X 2 + ⋯ + k s X s k_1X_1+k_2X_2+\dots +k_sX_s k1X1+k2X2+⋯+ksXs 为齐次线性方程组 A X = 0 \pmb{AX=0} AX=0 的解的充要条件是 k 1 + k 2 + ⋯ + k s = 0. k_1+k_2+\dots+k_s=0. k1+k2+⋯+ks=0.
是不是有点熟悉,特别像我们在微分方程中学的关于高阶线性微分方程的解的结构。
- 齐次解线性组合仍为齐次解。
- 齐次解 + 非齐次解为非齐次解。
- 非齐次解相减为齐次解。
- 非齐次解线性组合,系数之和为 1 才是非齐次解。
- 非齐次解线性组合,系数之和为 0 才是齐次解。
写在最后
线性方程组还有些内容,是关于计算的,我们放在后面来细说!
相关文章:

【考研数学】线性代数第四章 —— 线性方程组(1,基本概念 | 基本定理 | 解的结构)
文章目录 引言一、线性方程组的基本概念与表达形式二、线性方程组解的基本定理三、线性方程组解的结构写在最后 引言 继向量的学习后,一鼓作气,把线性方程组也解决了去。O.O 一、线性方程组的基本概念与表达形式 方程组 称为 n n n 元齐次线性方程组…...

使用Python写入数据到Excel:实战指南
在数据科学领域,Excel是一种广泛使用的电子表格工具,可以方便地进行数据管理和分析。然而,当数据规模较大或需要自动化处理时,手动操作Excel可能会变得繁琐。此时,使用Python编写程序将数据写入Excel文件是一个高效且便…...

接口测试总结分享(http与rpc)
接口测试是测试系统组件间接口的一种测试。接口测试主要用于检测外部系统与系统之间以及内部各个子系统之间的交互点。测试的重点是要检查数据的交换,传递和控制管理过程,以及系统间的相互逻辑依赖关系等。 一、了解一下HTTP与RPC 1. HTTP(H…...
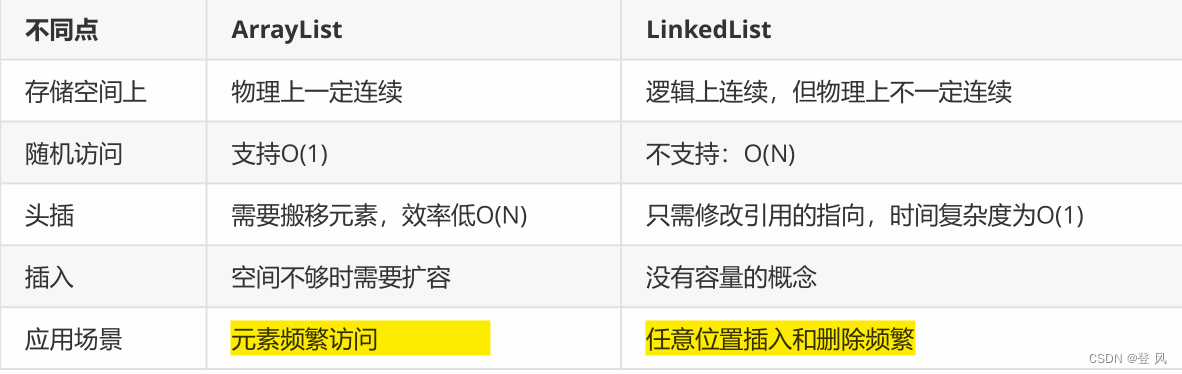
数据结构(Java实现)LinkedList与链表(下)
** ** 结论 让一个指针从链表起始位置开始遍历链表,同时让一个指针从判环时相遇点的位置开始绕环运行,两个指针都是每次均走一步,最终肯定会在入口点的位置相遇。 LinkedList的模拟实现 单个节点的实现 尾插 运行结果如下: 也…...
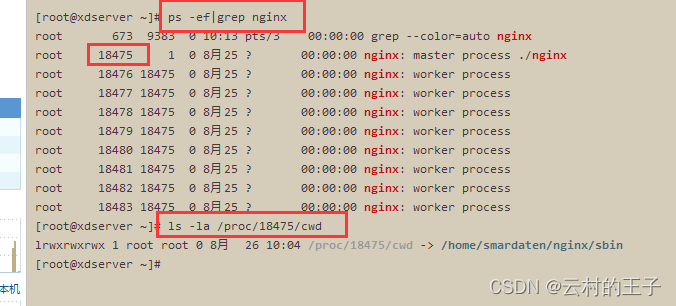
linux查看正在运行的nginx在哪个文件夹当中
1、查出Nginx进程PID ps -ef|grep nginx2、查看Nginx进程启动时的工作目录 ls -la /proc/<PID>/cwd将<PID>替换为第一步中列出的Nginx进程的PID。该命令会显示Nginx进程在启动时所在的工作目录(当前工作目录)...
Vue实现Excel表格中按钮增加小数位数,减少小数位数功能,多用于处理金融数据
效果图 <template><div><el-button click"increaseDecimals">A按钮</el-button><el-button click"roundNumber">B按钮</el-button><el-table :data"tableData" border><el-table-column v-for&q…...
自然语言处理(一):词嵌入
词嵌入 词嵌入(Word Embedding)是自然语言处理(NLP)中的一种技术,用于将文本中的单词映射到一个低维向量空间中。它是将文本中的单词表示为实数值向量的一种方式。 在传统的文本处理中,通常使用独热编码&…...
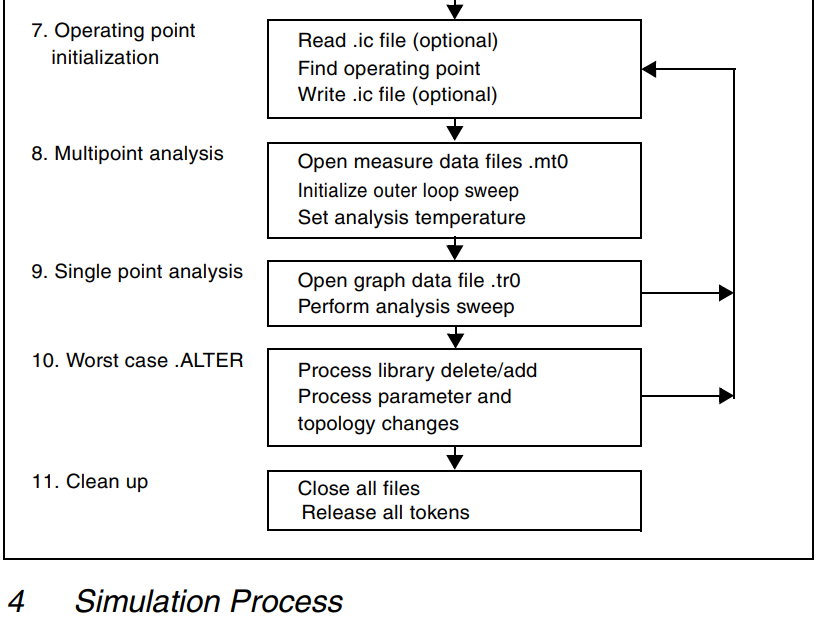
【HSPCIE仿真】HSPICE仿真基础
HSPICE概述 1. HSPICE简介3. 标准输入文件4. 标准输出文件3. HSPCIE仿真过程 1. HSPICE简介 SPICE (Simulation Program with IC Emphasis)是1972 年美国加利福尼亚大学柏克莱分校电机工程和计算机科学系开发 的用于集成电路性能分析的电路模拟程序。 …...
二、前端监控之方案调研
前端监控体系 一个完整的前端监控体系包括了日志采集、日志上报、日志存储、日志切分&计算、数据分析、告警等流程。 对于一名前端开发工程师来说,也就意味着工作不再局限于前端业务的开发工作,需要有Nginx服务运维能力、实时/离线分析能力、Node应…...

npm 创建 node.js 项目
package.json重要说明 package.json是创建任何node.js项目必须要有的一个文件。 因为在package.json文件中,有详细的项目描述, 包括: (1)项目名称:name (2)版本:version (3)依赖文件:dependencies 等…...

JMeter性能测试(上)
一、基础简介 界面 打开方式 双击 jmeter.bat双击 ApacheJMeter.jsr命令行输入 java -jar ApacheJMeter.jar 目录 BIN 目录:存放可执行文件和配置文件 docs目录:api文档,用于开发扩展组件 printable-docs目录:用户帮助手册 li…...

自定义date工具类 DateUtils.java
自定义date工具类 DateUtils.java 简介 Date日期类型的工具类。 api 日期格式化 format(Date date);日期格式化 format(Date date, String pattern);计算距离现在多久,非精确 getTimeBefore(Date date);计算距离现在多久,精确…...
Linux(Ubuntu)安装docker
2017年的3月1号之后,Docker 的版本命名开始发生变化,同时将 CE 版本和 EE 版本进行分开。 Docker社区版(CE):为了开发人员或小团队创建基于容器的应用,与团队成员分享和自动化的开发管道。docker-ce 提供了简单的安装…...
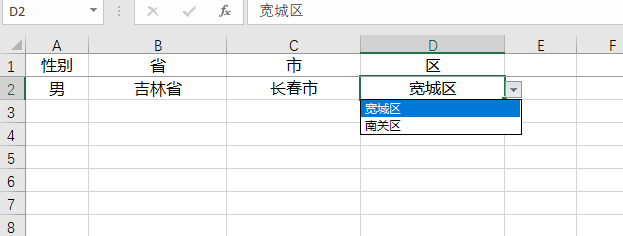
Apache Poi 实现Excel多级联动下拉框
由于最近做的功能,需要将接口返回的数据列表,输出到excel中,以供后续导入,且网上现有的封装,使用起来都较为麻烦,故参考已有做法封装了工具类。 使用apache poi实现excel联动下拉框思路 创建隐藏单元格&a…...

常见的 HTML<meta> 标签的 name 属性及其作用
HTML中的 <meta> 标签可以通过 name 属性提供元数据,这些元数据可以用于指定有关文档的信息,以及控制浏览器和搜索引擎的行为。name 属性通常与其他属性一起使用,如 content、charset、http-equiv 等,以提供更具体的元数据信…...
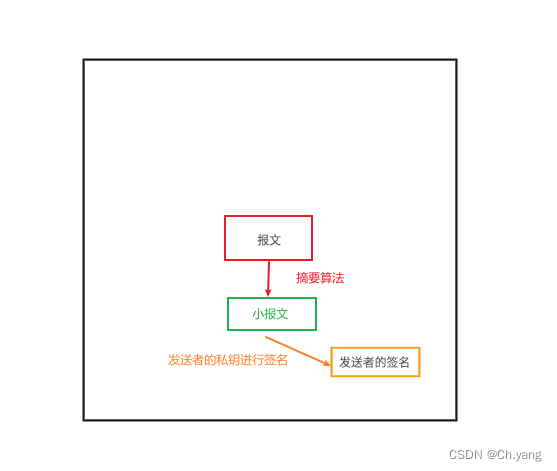
【网络安全】理解报文加密、数字签名能解决的实际问题
文章目录 前言1. 防止报文泄露 —— 加密体系的出现1.1 理解非对称加密体系的实施难点1.2 加密体系的实际应用 2. 防止报文被篡改 —— 数字签名的出现2.1 数字签名的原理2.2 数字签名的实施难点2.2 数字签名的实际应用 —— 引入摘要算法 3. 实体鉴别 —— CA证书 后记 前言 …...

linux中安装nodejs,卸载nodejs,更新nodejs
卸载nodejs 卸载node sudo apt-get remove nodejs清理掉自动安装的并且不需要软件包 sudo apt autoremove查看node相关的文件 sudo whereis node如果有文件需要手动删除文件 删除该文件命令 sudo rm -rf /usr/local/bin/node在此查看node -v 是未找到,说明你已经…...

浅谈Python网络爬虫应对反爬虫的技术对抗
在当今信息时代,数据是非常宝贵的资源。而作为一名专业的 Python 网络爬虫程序猿,在进行网页数据采集时经常会遭遇到各种针对爬虫行为的阻碍和限制,这就需要我们掌握一些应对反爬机制的技术手段。本文将从不同层面介绍如何使用 Python 进行网…...

代理池在过程中一直运行
Hey,爬虫达人们!在爬虫的过程中,要保持代理池的稳定性可不容易。今天就来和大家分享一些实用经验,教你如何让代理池在爬虫过程中一直运行!方法简单易行,让你的爬虫工作更顺畅. 在进行爬虫工作时࿰…...
基于Java+SpringBoot+Vue前后端分离党员教育和管理系统设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...
