【C++修炼之路】20.手撕红黑树
每一个不曾起舞的日子都是对生命的辜负
红黑树实现:RBTree
- 前言
- 一.红黑树的概念及性质
- 1.1 红黑树的概念
- 1.2 红黑树的性质
- 二.红黑树的结构
- 2.1 红黑树节点的定义
- 2.2 红黑树类的封装
- 三.红黑树的插入
- 情况1:只变色
- 情况2:变色+单旋
- 情况3:双旋
- 插入的代码实现:
- 四.红黑树的验证
- 五.红黑树实现代码(完整)
- RBTree.h
- Test.cpp
- 六.红黑树与AVL树的比较
前言
在上一节中我们学到了AVL树的结构及其相关性质,对于平衡树来说,AVL无疑是最完美的结构,但实际上AVL树由于完美的结构因此也要花费一定的代价,由于AVL树的结构很敏感,查找虽然最快,但插入节点后一旦偏离AVL结构就会进行旋转,而旋转就会花费一定的性能。因此我们提到的map和set的底层为了防止这种性能上的缺失,即便AVL是非常完美的结构,也不采用AVL。而是采用我们这节所要描述的红黑树。
一.红黑树的概念及性质
1.1 红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
可见红黑树的这种结构,虽然在不满足条件时会发生旋转,但敏感程度相比AVl树大大降低。
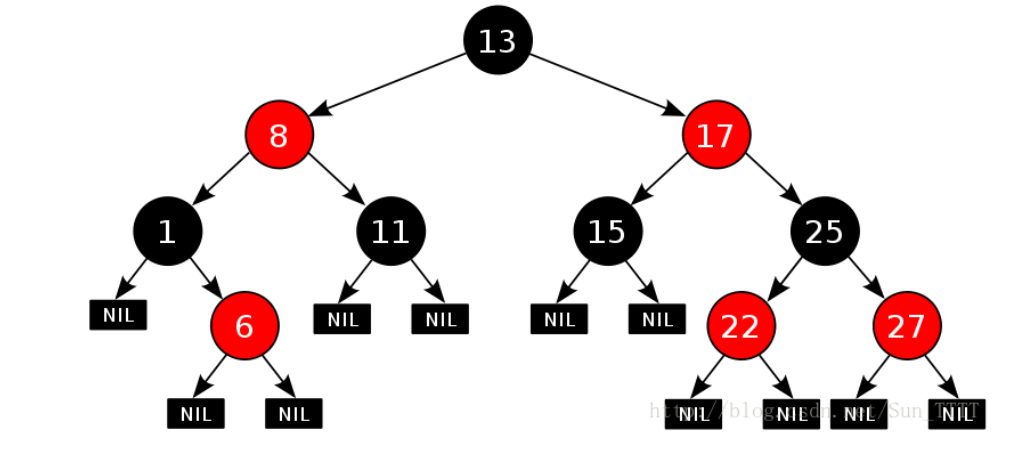
1.2 红黑树的性质
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
需要注意的是:对于性质3,意思就是没有连续的红色结点。
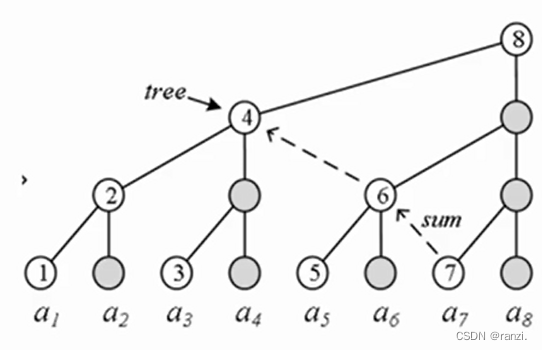
思考: 为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
就上面的这颗红黑树来说,有11条路径(需算到空)我们只观察黑色结点,发现是接近满二叉树的。对于红黑树的最短路径,最短的极限情况就是一条路径全是黑色的结点,因为其他路径也会有相同数目的黑节点加上一定数量的红色结点,而最长路径就是一黑一红相间的路径。可见,最长的结点个数是最短结点个数的二倍。
这样就是红黑树的结构,且存在最长和最短的情况,最短为最长的二分之一。
由于红黑树确保没有一条路径会比其他路径长出俩倍,因此可以看成近似平衡,对于这种不确定的结构,自然就有最好的情况和最坏的情况。
- 最好情况:(左右平衡)
全黑或者每条路径都是一黑一红相间的路径,接近满二叉树。那么此时设全黑的路径长度为h结点数量为N,则2^h - 1 + _ = N(_代表红色结点,由于一条路径红色结点数量一定小于等于黑色,所以可以忽略计算)此时,h = logN。
- 最坏情况:(左右极其不平衡)
左子树全黑,且右子树一黑一红。那么此时最长路径为2*logN。
总结: 可以看出,在对数的加持下,即便是最坏情况,对于计算机来说相差也不是很大。虽不如AVL的极度平衡,但红黑树明显在插入节点时显得张弛有力。对于AVL来说,说是过刚易折也不为过,往往像红黑树那样增加一定的柔韧性,才是最后的选择。
二.红黑树的结构
2.1 红黑树节点的定义
相比较AVL树,红黑树的结点仍是三叉链这个结构,为后续不满足结构的条件旋转做准备。此外,和AVL树结点不同的是,红黑树不再有平衡因子这一变量,而是多了一个定义颜色的变量,颜色变量通过枚举实现。下面看看结点定义的代码:
enum Color//颜色采用枚举,但STL库采用的是特殊的bool值,后续会看
{RED,//0BLACK,//1
};template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED)//默认哪种颜色都可以,因为后续会改{}};
2.2 红黑树类的封装
enum Color//颜色采用枚举,但STL库采用的是特殊的bool值,后续会看
{RED,//0BLACK,//1
};template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;RBTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED)//默认哪种颜色都可以,因为后续会改{}};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public://成员函数bool Insert(const pair<K, V>& kv){}
private:Node* _root = nullptr;
};
三.红黑树的插入
与AVL树一样,在插入中需要考虑的因素众多,但相比AVL,红黑树在插入时的情况少很多,因为其结构没有AVL树的高度平衡。
在红黑树的性质中,第三,第四条尤为重要。即:
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
如果我们新插入的结点的颜色为黑的话,插入之后一定会打破上述第二个结构,导致每条路径的黑结点数量不同;如果新插入的节点的颜色为红色的话,也有可能不满足情况,如果插入节点的父节点为黑的话还好,但如果父节点为红,也就不满足这个条件了。因此,插入节点的颜色尤为重要,经过上述考虑,插入节点的颜色为红无疑是最好的选择,因为有可能满足条件,有可能不满足条件,但插入黑色一定不满足。如果插入红色的也不满足,那就后期处理就好了。
- 插入节点的颜色必须为红
检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
约定: cur为当前(插入)节点,p为父节点,g为祖父节点,u为叔叔节点
对于新节点的插入,与父节点和父节点的兄弟节点也有关,下面就看看各种情况:
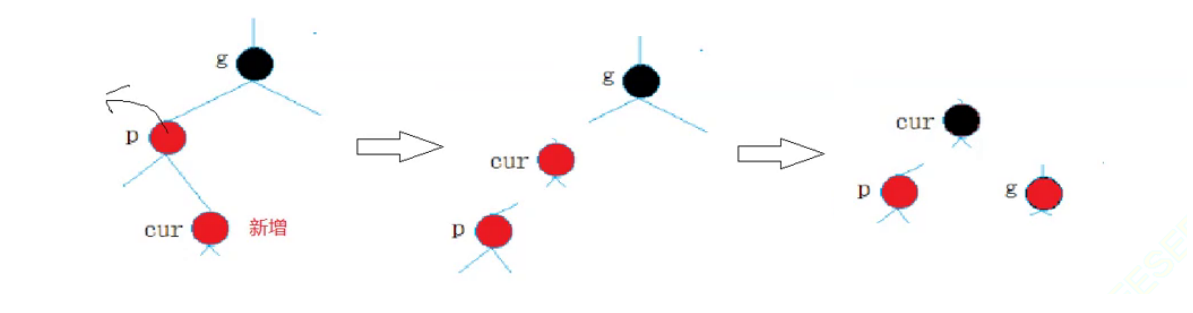
情况1:只变色
- cur为红,p为红,g为黑,u存在且为红
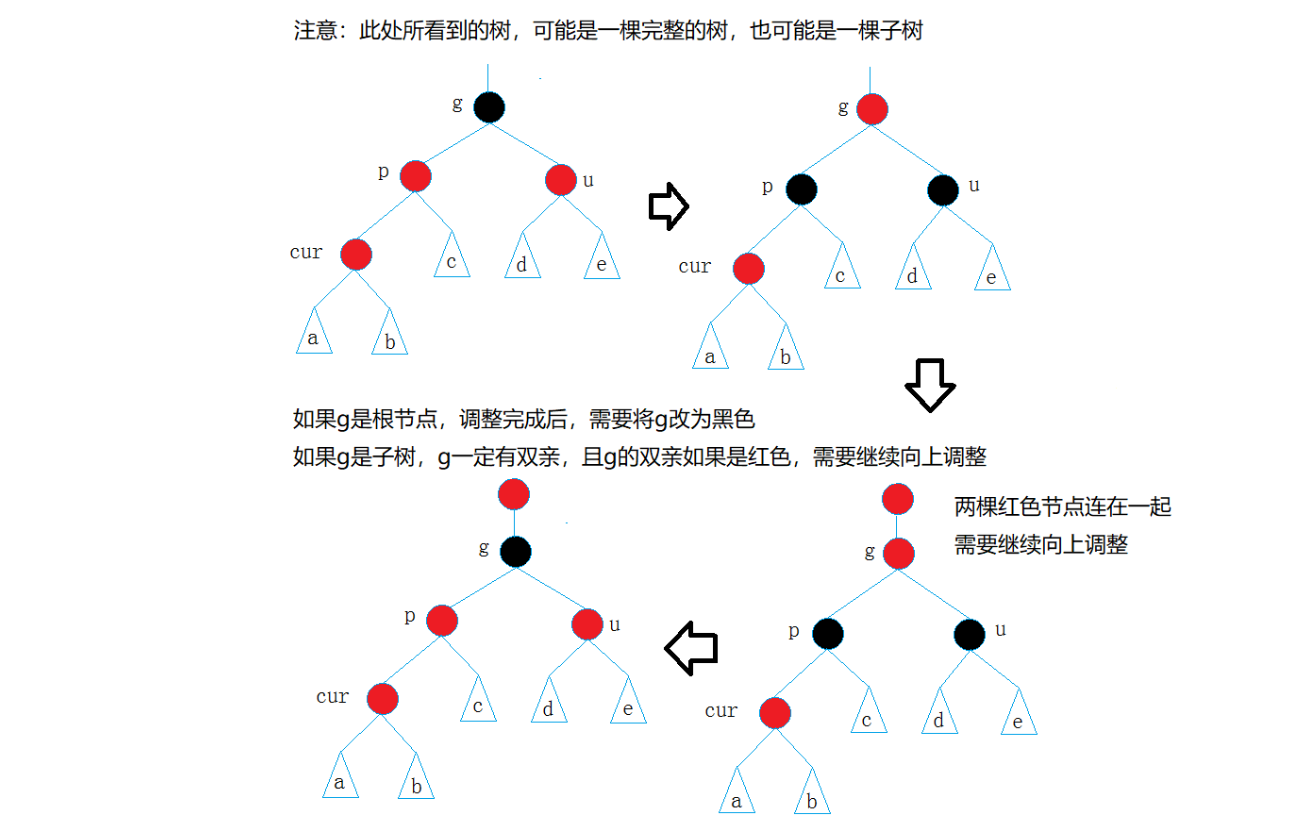
通过上面图的步骤,我们大致知道了思路,如果红色结点连续,为了满足红黑树的不能有连续红色结点的性质,我们需要将其双亲也就是父亲结点变成黑色,如果这棵树是子树,那么为了保证黑色结点数量不变,我们需要将g变红,如果g的双亲仍是红色,那么就一直往上更新迭代。对于上图,实际上同样是个抽象图,因为a,b,c,d,e可以使任意的红黑树子树,情况也会随着这几个抽象树节点的增加而变化的非常多,因此我们只需要牢记这种抽象图即可。
cur和p均为红,违反了性质三,此处能否将p直接改为黑?
解决方式:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
可以看出,红色结点的增加是因为插入节点,黑色节点的增加是为了保证红黑树结构的性质从红色结点变化而来的。
情况2:变色+单旋
- cur为红,p为红,g为黑,u不存在/u存在且为黑
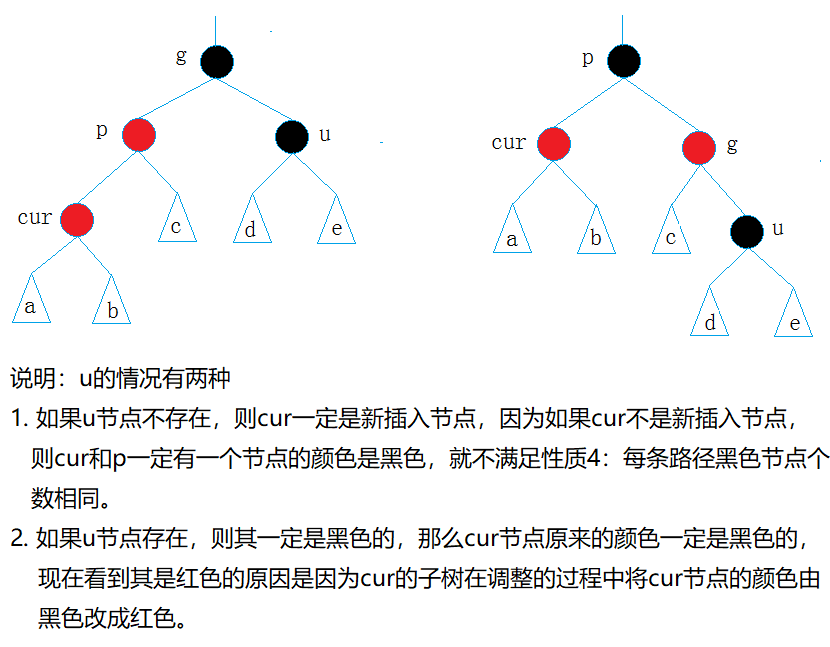
如果不存在叔叔结点u,那么是这样的结构: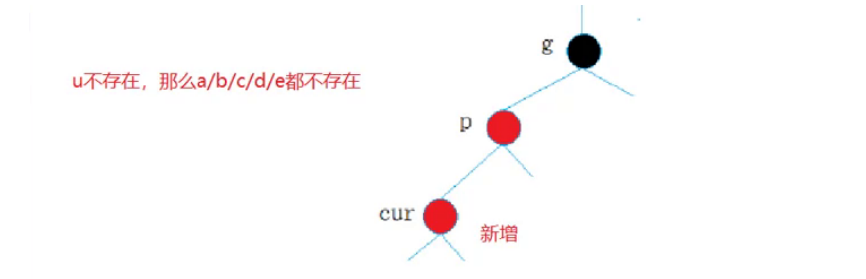
此时,新增的cur节点为红,那我们必须想办法将p变黑,此时就可以考虑将g为轴进行旋转的方式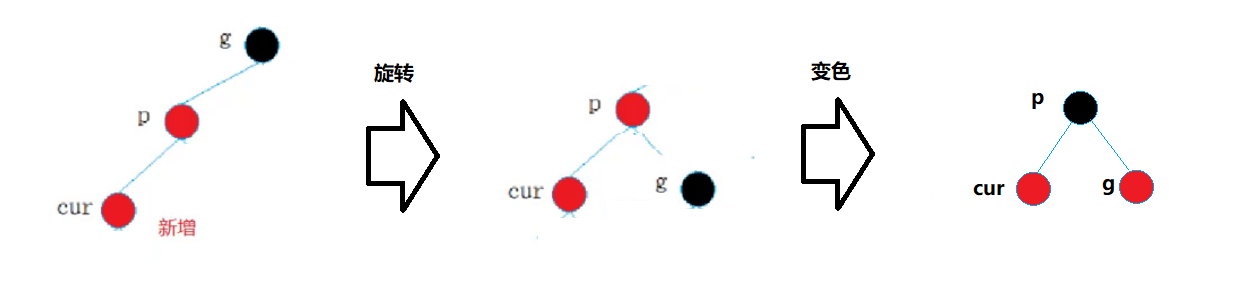
这样,就可以使其满足红黑树的结构了,u结点存在且为黑和此同理。
接下来看看步骤:
p为g的左孩子,cur为p的左孩子,则g进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则g进行左单旋转
p、g变色–p变黑,g变红
情况3:双旋
- cur为红,p为红,g为黑,u不存在/u存在且为黑
看似与情况二一样,实际上区别是cur插入的左右不同。情况2为左,情况3为右。
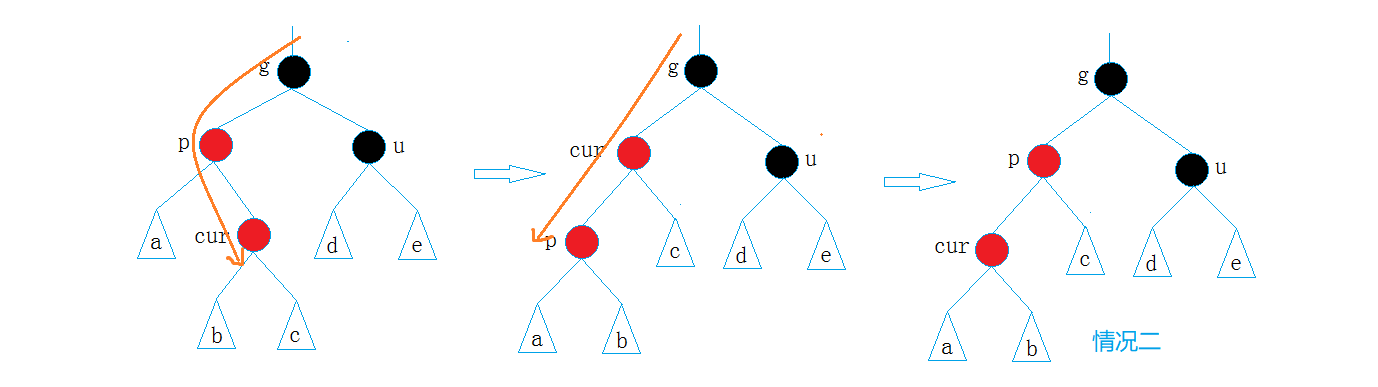
和上篇中的AVL一样,对于这种弯的结构,只进行一次旋转是不可能成功的,因此需要进行两部旋转,上图只旋转了一次,变成了情况2,因此需要再旋转一次,就能满足红黑树结构的性质。
步骤:
- p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,p为g的右孩子,cur为p的左孩子,则针对p做右单旋转。
则转换成了情况2。转换成情况2之后,再根据情况2的步骤继续旋转: - p为g的左孩子,cur为p的左孩子,则g进行右单旋转;相反,p为g的右孩子,cur为p的右孩子,则g进行左单旋转
p、g变色–p变黑,g变红
注意,经过左旋,变色位置不变,但对应位置的结点变了,因此在代码编写时需注意这个问题。
插入的代码实现:
注:Insert单拿出来观察,其利用的旋转函数与AVL一样,只不过去掉了平衡因子。
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点为黑色return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;//重要,插入的结点初始化成红色if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED)//如果父亲的颜色为红,才需要去处理{Node* grandfather = parent->_parent;//找到祖父才能找到叔叔if (parent == grandfather->_left){Node* uncle = grandfather->_right;//看叔叔颜色//情况1:uncle存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况2或3:不用考虑叔叔的问题,即叔叔为空还是为黑{if (cur == parent->_left)//情况2{// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//情况3{// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//与上述代码的左右反过来了而已,步骤一样但左右相反。{Node* uncle = grandfather->_left;//情况1if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况2和3{// g// p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}}}}_root->_col = BLACK;return true;
}
此外,有插入就有删除,删除是插入的反向思维。删除太难了,不用学。真想了解看这个,但是没有代码:红黑树 - Never - 博客园 (cnblogs.com)
四.红黑树的验证
红黑树的检测分为两步:
- 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 检测其是否满足红黑树的性质
函数代码:
bool IsBalance()//检查是否为红黑树结构
{if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}//遍历这棵树,就好了,检查是否存在连续的红结点。//检查父亲,因为孩子不一定有,但是一定有父亲return Check(_root, 0, ref);
}
bool Check(Node* root, int blackNum, int ref)
{if (root == nullptr){if (blackNum != ref){cout << "违反规则:一条路径上的黑色节点数量不同" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则,出现连续红色结点" << endl;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);
}
五.红黑树实现代码(完整)
随机插入构建红黑树:
以升序插入构建红黑树:
以降序插入构建红黑树:
RBTree.h
#pragma onceenum Color//颜色采用枚举,但STL库采用的是特殊的bool值,后续会看
{RED,//0BLACK//1
};template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;Color _col;RBTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点为黑色return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;//重要,插入的结点初始化成红色if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}while (parent && parent->_col == RED)//如果父亲的颜色为红,才需要去处理{Node* grandfather = parent->_parent;//找到祖父才能找到叔叔if (parent == grandfather->_left){Node* uncle = grandfather->_right;//看叔叔颜色//情况1:uncle存在且为红if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况2或3:不用考虑叔叔的问题,即叔叔为空还是为黑{if (cur == parent->_left)//情况2{// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//情况3{// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else//与上述代码的左右反过来了而已,步骤一样但左右相反。{Node* uncle = grandfather->_left;//情况1if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else//情况2和3{// g// p// cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}}}}_root->_col = BLACK;return true;}//旋转代码和AVL一样,只是去掉了平衡因子void RotateL(Node* parent)//左单旋{//1.记录subR, subRLNode* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)//subRL不为空则需要连接到parent{subRL->_parent = parent;}Node* ppNode = parent->_parent;//记录保存subR->_left = parent;parent->_parent = subR;if (ppNode == nullptr)//说明根节点变化{_root = subR;_root->_parent = nullptr;}else//如果是局部子树{//判断ppNode之前是左连接还是右连接if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (ppNode == nullptr){_root = subL;_root->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}void Inorder(){_Inorder(_root);}bool IsBalance()//检查是否为红黑树结构{if (_root == nullptr){return true;}if (_root->_col != BLACK){return false;}int ref = 0;Node* left = _root;while (left){if (left->_col == BLACK){++ref;}left = left->_left;}//遍历这棵树,就好了,检查是否存在连续的红结点。//检查父亲,因为孩子不一定有,但是一定有父亲return Check(_root, 0, ref);}private:bool Check(Node* root, int blackNum, int ref){if (root == nullptr){if (blackNum != ref){cout << "违反规则:一条路径上的黑色节点数量不同" << endl;return false;}return true;}if (root->_col == RED && root->_parent->_col == RED){cout << "违反规则,出现连续红色结点" << endl;}if (root->_col == BLACK){++blackNum;}return Check(root->_left, blackNum, ref)&& Check(root->_right, blackNum, ref);}void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}Node* _root = nullptr;
};void TestRBTree1()
{int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.Inorder();}
Test.cpp
#include<iostream>
#include<string>
#include<map>
#include<assert.h>
using namespace std;
#include"RBTree.h"
int main()
{TestRBTree1();return 0;
}
六.红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(log2Nlog_2 Nlog2N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
相关文章:

【C++修炼之路】20.手撕红黑树
每一个不曾起舞的日子都是对生命的辜负 红黑树实现:RBTree 前言一.红黑树的概念及性质1.1 红黑树的概念1.2 红黑树的性质二.红黑树的结构2.1 红黑树节点的定义2.2 红黑树类的封装三.红黑树的插入情况1:只变色情况2:变色单旋情况3:双旋插入的代…...
树状数组(高级数据结构)-蓝桥杯
一、简介树状数组 (Binary Indexed Tree,BIT),利用数的二进制特征进行检索的一种树状结构。一种真正的高级数据结构: 二分思想、二叉树、位运算、前缀和。高效!代码极其简洁!二、基本应用数列a1,a2,....,an,操作:单点修改…...
Flink-多流转换(Union、Connect、Join)
文章目录多流转换分流基本合流操作联合(Union)连接(Connect)基于时间的合流——双流联结(Join)窗口联结(Window Join)间隔联结(Interval Join)窗口同组联结&a…...
kubeadmin安装k8s集群
目录 一 、环境部署 1、服务器规划 2、环境准备 二、所有节点安装docker 1、配置yum源,安装docker 2、配置daemon.json文件 三、所有节点安装kubeadm、kubelet 和kubectl 四、部署k8s集群 1、查看初始化需要的镜像 2、导入镜像 3、初始化kubeadm 3.1 方…...
java3月train笔记
java笔记 day01 一、jdk和idea下载及安装(一般不建议装C盘): jdk:java开发环境 idea:开发工具(软件),用来编写代码的 苍老师文档服务器:doc.canglaoshi.org jdk下载&…...
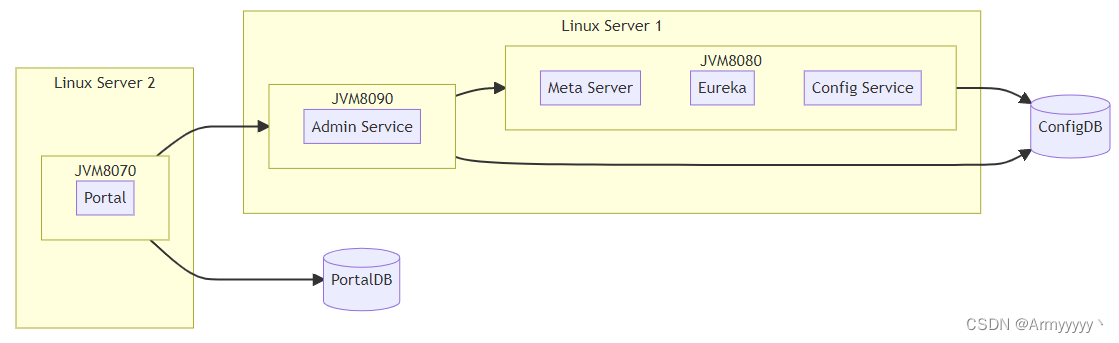
Apollo Config原理浅析
文章目录1. 简介2. 基本功能3. Apollo关键功能实现原理3.1 框架整体原理3.1.1 Apollo角色3.1.2 框架执行原理3.1.3 整体组成3.2 细节实现3.2.1 Eureka和不同角色机器的关系3.2.2 Meta Server的作用3.2.3 ReleaseMessage消息实现原理3.2.4 Client的通信方式1. 简介 apollo是携程…...
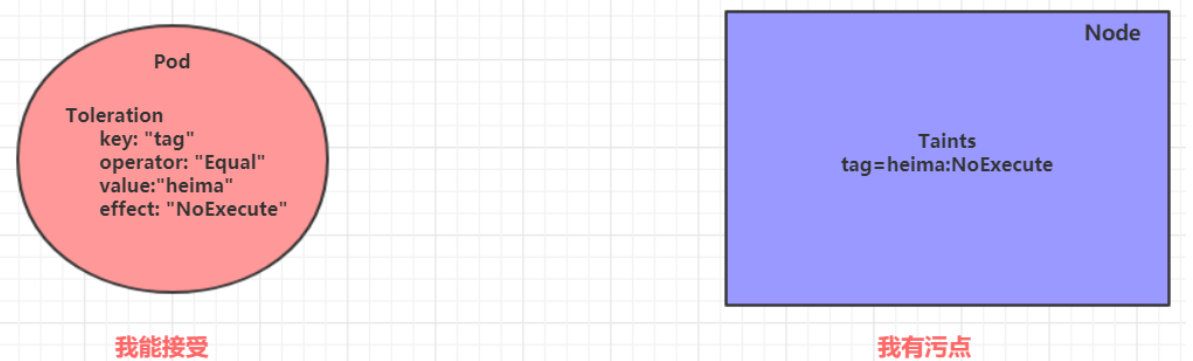
Kubernetes二 Kubernetes之实战以及pod详解
Kubernetes入门 一 Kubernetes实战 本章节将介绍如何在kubernetes集群中部署一个nginx服务,并且能够对其进行访问。 1.1 Namespace Namespace是kubernetes系统中的一种非常重要资源,它的主要作用是用来实现多套环境的资源隔离或者多租户的资源隔离。…...

机械革命黑苹果改造计划第四番-外接显示器、win时间不正确问题解决
问题 1.无法外接显示器 最大的问题就是目前无法外接显示器,因为机械革命大多数型号笔记本电脑的HDMI、DP接口都是直接物理接在独显上的,内屏用核显外接显示器接独显,英伟达独显也是黑苹果无法驱动的,而且发现机械革命tpyec接口还…...
Linux docker(03)可使用GPU渲染的x11docker实战总结
该系列文章的目的旨在之前的章节基础上,使用x11docker构建一个可以使用GPU的docker容器。该容器可以用于3D图形渲染/XR 等使用GPU渲染的程序调试和运行。 0 why docker 为什么非要用x11docker,而不是其他的docker呢? 因为一般的docker是不…...

【Linux操作系统】【综合实验一 Linux操作基础】
文章目录一、实验目的二、实验要求三、实验内容四、实验报告要求一、实验目的 要求掌握Linux基础操作,熟悉Linux行界面,并明白操作的原理以及目的;熟悉Linux系统环境。 二、实验要求 通过这个第一阶段实验,要求掌握以下操作与相…...

关于监控服务器指标、CPU、内存、警报的一些解决方案
文章目录关于监控服务器指标、CPU、内存、警报的一些解决方案Prometheus Grafana 配置 IRIS / Cach 监控服务器Prometheus简介特点架构图Grafana简介特点配置流程自定义Prometheus接口定义配置 Exporter 监控服务器系统资源简介配置流程使用 Alertmanager报警简介配置流程基于…...
)
vue3全家桶技术栈基础(一)
在认识vue3全家桶之前,先简单回顾一下vue2的全家桶 一.在vue2中,全家桶技术栈 技术栈: vue2 vue-cli vuex3vue-router3webpack elementUI 1.vue-cli 脚手架构建vue项目,CLI 服务是构建于 webpack 和 webpack-dev-server构建快速生成一个vue2的开发项…...
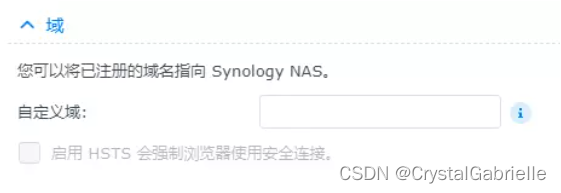
群晖-第2章-设置HTTPS访问
群晖-第2章-设置HTTPS访问 本章介绍如何通过HTTPS访问群晖,前置要求是完成群晖-第1章-IPV6的DDNS中的内容,可以是IPV4也可以是IPV6,或者你有公网IP,直接添加DNS解析也可以。只要能通过域名访问到nas就行。 本文参考自群晖添加SS…...
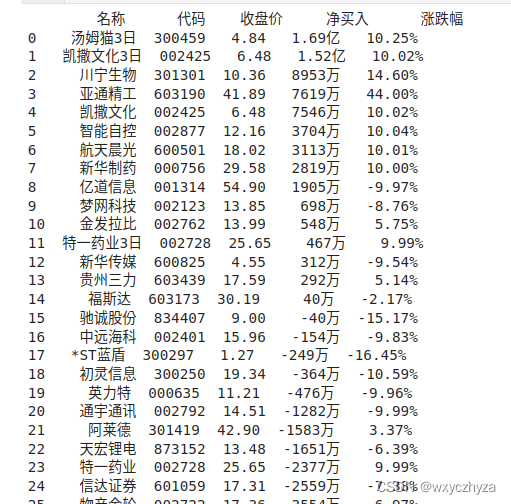
005 利用fidder抓取app的api,获得股票数据
一、下载安装fidder 百度搜索fidder直接下载,按提示安装即可。 二、配置fidder 1. 打开fidder,选择tools——options。 2. 选择HTTPS选项卡,勾选前三项,然后点击右侧【actions】,选择【trust root certificate】&a…...
京东测试进阶之路:初入测试碎碎念篇
1、基本的测试用例设计方法 基本的测试用例设计方法(边界值分析、等价类划分等)。 业务和场景的积累,了解测试需求以及易出现的bug的地方。 多维角度设计测试用例(用户、业务流程、异常场景、代码逻辑)。 2、需求分析 …...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 乘积最大值(JavaScript) | 机试题+算法思路+考点+代码解析 【2023】
乘积最大值 题目 给定一个元素类型为小写字符串的数组 请计算两个没有相同字符的元素长度乘积的最大值 如果没有符合条件的两个元素返回0 输入 输入为一个半角逗号分割的小写字符串数组 2 <= 数组长度 <= 100 0 < 字符串长度 <= 50 输出 两个没有相同字符的元…...
Java并发知识点
文章目录1. start()和run()方法的区别?2. volatile关键字的作用?使用volatile能够保证:防止指令重排3. sleep方法和wait方法有什么区别?sleep()方法4. 如何停止一个正在运行的线程?方法一:方法二࿱…...
前端 ES6 环境下 require 动态引入图片以及问题
前端 ES6 环境下 require 动态引入图片以及问题require 引入图片方式打包体积对比总结ES6 环境中,通过 require 的方式引入图片很方便,一直以来也没有出过什么问题,后来项目中,需要动态引入图片。 require 动态引入也容易实现&am…...

PCL 欧氏聚类分割
文章目录 一、应用背景1、点云分割算法的属性2、点云分割的挑战二、实现过程三、主要函数及代码实现1、主要函数2、核心代码3、效果实现四、参考文献一、应用背景 1、点云分割算法的属性 1)鲁棒性,比如树木是具有与汽车相区别的特征的,当点云数据的特征数量增加时,分割算…...

一台服务器最大能支持多少条TCP连接
一、一台服务器最大能打开的文件数 1、限制参数 我们知道在Linux中一切皆文件,那么一台服务器最大能打开多少个文件呢?Linux上能打开的最大文件数量受三个参数影响,分别是: fs.file-max (系统级别参数)&am…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

