十大排序算法
一、冒泡排序
冒泡排序(Bubble Sort)是一种简单直观的排序算法。它重复地走访要排序的数列,一次比
较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经交换慢慢"浮"到数列的头部。
/*** 冒泡排序*/
public class BubbleSort {public void sort(int[] arr) {if (arr == null || arr.length == 0) {return;}for (int i = 1; i < arr.length; i++) { //比较的轮数for (int j = 0; j < arr.length - i; j++) { // 每轮比较的次数if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}}
}
二、选择排序
选择排序也是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以
用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。
public class SelectionSort {public void sort(int[] arr) {if (arr == null || arr.length == 0) {return;}for (int i = 0; i < arr.length - 1; i++) { //比较的轮数int min = i;// 记录最小值的索引for (int j = i + 1; j < arr.length; j++) {if (arr[min] > arr[j]) {min = j;}}// 将最小值放置在索引为i的位置if (min != i) {int temp = arr[i];arr[i] = arr[min];arr[min] = temp;}}}
}三、插入排序
插入排序的代码实现虽然没有冒泡排序和选择排序那么简单粗暴,但它的原理应该是最容易理
解的了,因为只要打过扑克牌的人都应该能够秒懂。插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
public class InsertSort {public void sort(int[] arr) {if (arr == null || arr.length == 0) {return;}for (int i = 1; i < arr.length; i++) {int instartVal = arr[i];int j = i - 1; // 有序区最后一个元素while (j >= 0) {if (arr[j] > instartVal) {arr[j + 1] = arr[j];j--;} else {break;}}arr[j + 1] = instartVal;}}
}四、希尔排序
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
• 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
• 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位;
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排
序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
public class ShellSort {public void sort(int[] arr) {if (arr == null || arr.length == 0) {return;}int length = arr.length;// step:表示希尔增量for (int step = length / 2; step >= 1; step /= 2) {//从setp位置开始进行插入排序,直至完毕for (int i = step; i < arr.length; i++) {int instartVal = arr[i];int j = i - step; // 有序区最后一个元素while (j >= 0) {if (arr[j] > instartVal) {arr[j + step] = arr[j];j -= step;} else {break;}}arr[j + step] = instartVal;}}}
}五、 归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法
(Divide and Conquer)的一个非常典型的应用。
1. 算法步骤
1. 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
2. 设定两个指针,最初位置分别为两个已经排序序列的起始位置;
3. 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
4. 重复步骤 3 直到某一指针达到序列尾;
5. 将另一序列剩下的所有元素直接复制到合并序列尾。
import java.util.Arrays;/*** 归并排序*/
public class MergeSort {public int[] sort(int[] arr) {if (arr == null || arr.length < 2) {return arr;}int middle = (int) Math.floor(arr.length / 2);int[] left = Arrays.copyOfRange(arr, 0, middle );int[] right = Arrays.copyOfRange(arr, middle , arr.length);return merge(sort(left), sort(right));}protected int[] merge(int[] left, int[] right) {int[] result = new int[left.length + right.length];int i = 0;int m = 0;int n = 0;while (m < left.length && n < right.length) {if (left[m] <= right[n]) {result[i++] = left[m++];} else {result[i++] = right[n++];}}while (m < left.length) {result[i++] = left[m++];}while (n < right.length) {result[i++] = right[n++];}return result;}
}六、 快速排序
1. 算法步骤
1. 从数列中挑出一个元素,称为 "基准"(pivot);
2. 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
3. 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
/*** 快速排序*/
public class FastSort {public void sort(int[] arr) {if (arr == null || arr.length < 2) {return;}// 排序fastSort(arr, 0, arr.length - 1);}// 对[left,right]区间进行排序private void fastSort(int[] arr, int left, int right) {// 递归到底的情况if (left >= right) {return;}// 递归操作int pivot = arr[left];int i = left;int j = right;while (i < j) {// 从右边开始找到第一个小于pivot的元素while (i < j && arr[j] > pivot) {j--;}// 替换if (i < j) {arr[i] = arr[j];i++;}// 从左边开始找到第一个比pivot大的元素while (i < j && arr[i] < pivot) {i++;}// 替换if (i < j) {arr[j] = arr[i];j--;}}arr[i] = pivot;fastSort(arr, left, i - 1);fastSort(arr, i + 1, right);}
}
七、 堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列;
小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列;
堆排序的平均时间复杂度为 Ο(nlogn)。
1. 算法步骤
1. 创建一个堆 H[0……n-1];
2. 把堆首(最大值)和堆尾互换;
3. 调用 shift_down方法,使除过堆尾元素的树满足最大堆的性质;
4. 重复步骤 2,直到堆中只有一个元素。
// 堆排序
public class HeapSort {private int getParentIndex(int index) {if (index < 0) {throw new IllegalArgumentException("index is invalid!");}if (index == 0) { // 处理根节点return -1;}return (index - 1) / 2;}// 根据当前结点所在数组的索引获取左孩子结点的索引private int getLeftChildIndex(int index) {return 2 * index + 1;}public void sort(int[] arr) {if (arr == null || arr.length == 0) {return;}// 将完全二叉树整理成堆heapify(arr);// 排序for (int i = arr.length - 1; i > 0; i--) {// 将堆尾元素与堆首元素互换int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 整理成堆siftDown(0, arr, i);}}private void heapify(int[] arr) {// 1、找到最后一个元素的父节点int parentIndex = getParentIndex(arr.length - 1);// 2、从最后一个元素的父节点开始下沉操作,直到根节点for (; parentIndex >= 0; parentIndex--) {siftDown(parentIndex, arr, arr.length);}}private void siftDown(int curIndex, int[] arr, int length) {int leftChildIndex = getLeftChildIndex(curIndex);int chageIndex = leftChildIndex;while (leftChildIndex < length) {int rigthChildIndex = leftChildIndex + 1;if (rigthChildIndex < length && arr[rigthChildIndex] > arr[leftChildIndex]) {chageIndex = rigthChildIndex;}if (arr[chageIndex] > arr[curIndex]) {// 交换操作int temp = arr[curIndex];arr[curIndex] = arr[chageIndex];arr[chageIndex] = temp;curIndex = chageIndex;leftChildIndex = getLeftChildIndex(curIndex);chageIndex = leftChildIndex;} else {break;}}}
}
八、 计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
1. 计数排序的特征当输入的元素是 n 个 0 到 k 之间的整数时,它的运行时间是 O(n + k)。计数排序不是比较排序,排序的速度快于任何比较排序算法。由于用来计数的数组C的长度取决于待排序数组中数据的范围(等于待排序数组的最大值与最小值的差加上1),这使得计数排序对于数据范围很大的数组,需要大量时间和内存。通俗地理解,例如有 10 个年龄不同的人,统计出有 8 个人的年龄比 A 小,那 A 的年龄就排在第9 位,用这个方法可以得到其他每个人的位置,也就排好了序。当然,年龄有重复时需要特殊处理(保证稳定性),这就是为什么最后要反向填充目标数组,以及将每个数字的统计减去 1 的原因。
2、算法步骤
(1)找出待排序的数组中最大和最小的元素
(2)统计数组中每个值为i的元素出现的次数,存入数组C的第i项
(3)对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
(4)反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
public class CountingSort {public void sort(int[] arr) {if (arr == null || arr.length < 2) {return;}// 获取数组中最大的值int maxVal = getMaxVal(arr);// 创建一个数组,用来计数int[] counts = new int[maxVal + 1];// 计数for (int i = 0; i < arr.length; i++) {counts[arr[i]]++;}// 反向填充int index = 0;for (int i = 0; i < counts.length; i++) {while (counts[i] > 0) {arr[index++] = i;counts[i]--;}}}private int getMaxVal(int[] arr) {int max = arr[0];for (int i = 1; i < arr.length; i++) {max = Math.max(max, arr[i]);}return max;}
}九、 桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
• 在额外空间充足的情况下,尽量增大桶的数量
• 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
1. 什么时候最快
当输入的数据可以均匀的分配到每一个桶中。
2. 什么时候最慢
当输入的数据被分配到了同一个桶中。
import java.util.ArrayList;
import java.util.List;// 桶排序
public class BucketSort {public void sort(int[] arr) {if (arr == null || arr.length < 2) {return;}// 创建桶List<Integer>[] buckets = new ArrayList[10];// 初始化桶for (int i = 0; i < buckets.length; i++) {buckets[i] = new ArrayList<>();}// 将数据放入桶中for (int i = 0; i < arr.length; i++) {int index = arr[i] / 10;buckets[index].add(arr[i]);}//分别堆每个桶进行排序for (int i = 0; i < buckets.length; i++) {buckets[i].sort(null);}// 将桶中的元素反向填充到arr中int index = 0;for (int i = 0; i < buckets.length; i++) {List<Integer> item = buckets[i];while (!item.isEmpty()) {arr[index++] = item.remove(0);}}}
}
十、 基数排序
原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。基数排序的方式可以采用
LSD(Least significant digital)或MSD(Most significant digital),LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
MSD:先从高位开始进行排序,在每个关键字上,可采用计数排序
LSD:先从低位开始进行排序,在每个关键字上,可采用桶排序
1. 基数排序 vs 计数排序 vs 桶排序
基数排序有两种方法:
这三种排序算法都利用了桶的概念,但对桶的使用方法上有明显差异:
• 基数排序:根据键值的每位数字来分配桶;
• 计数排序:每个桶只存储单一键值;
• 桶排序:每个桶存储一定范围的数值;
import java.util.ArrayList;
import java.util.List;/*** 计数排序*/
public class RadixSort {public void sort(int[] arr) {if (arr == null || arr.length < 2) {return;}// 获取最大值int maxValue = getMaxVal(arr);// 获取最大位数int maxDigit = getMaxDigit(maxValue);radixSort(arr, maxDigit);}private void radixSort(int[] arr, int maxDigit) {int mod = 10;// 模数int dev = 1;for (int i = 0; i < maxDigit; i++) { // 比较轮数// 创建桶List<Integer>[] bucket = new ArrayList[10];// 对桶进行初始化for (int n = 0; n < bucket.length; n++) {bucket[n] = new ArrayList<>();}for (int j = 0; j < arr.length; j++) {int bucketIndex = (arr[j] / dev) % mod;bucket[bucketIndex].add(arr[j]);}// 对桶进行排序//分别堆每个桶进行排序for (int k = 0; k < bucket.length; k++) {bucket[k].sort(null);}// 将桶中的元素反向填充到arr中int index = 0;for (int m = 0; m < bucket.length; m++) {List<Integer> item = bucket[m];while (!item.isEmpty()) {arr[index++] = item.remove(0);}}dev = dev * 10;}}private int getMaxDigit(int maxValue) {int length = 1;int curNum = maxValue;while (curNum / 10 != 0) {curNum = curNum / 10;length++;}return length;}private int getMaxVal(int[] arr) {int max = arr[0];for (int i = 1; i < arr.length; i++) {max = Math.max(max, arr[i]);}return max;}
}
相关文章:

十大排序算法
一、冒泡排序 冒泡排序(Bubble Sort)是一种简单直观的排序算法。它重复地走访要排序的数列,一次比 较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经…...

PIP 常用操作汇总
1. 升级 python -m pip install --upgrade pip2. 列出所有安装包 pip list3. 查找特定包 pip list | findstr xxx4. 查看特定包 pip show xxx5. 安装软件包 pip install pyzmq24.0.16. 卸载软件包 pip uninstall -y pyzmq7. 查看配置 # 生效的配置(global -&…...

线性代数的本质笔记(3B1B课程)
文章目录 前言向量矩阵行列式线性方程非方阵点积叉积基变换特征向量与特征值抽象向量空间 前言 最近在复习线代,李永乐的基础课我刷了一下,感觉讲的不够透彻,和我当年学线代的感觉一样,就是不够形象。 比如,行列式为…...

快速掌握MQ消息中间件rabbitmq
快速掌握MQ消息中间件rabbitmq 目录概述需求: 设计思路实现思路分析1.video 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for change,c…...

Git push拦截
遇到的问题 今天想提交代码到gitee,结果发现被拦截了,有段提示“forbidden by xxxx”… 我记得xxxx好像是公司的一个防泄密的东西… 这个东西是怎么实现的呢? 解决 原来git提供很多hook,push命令就有一个pre-push的hook&#x…...
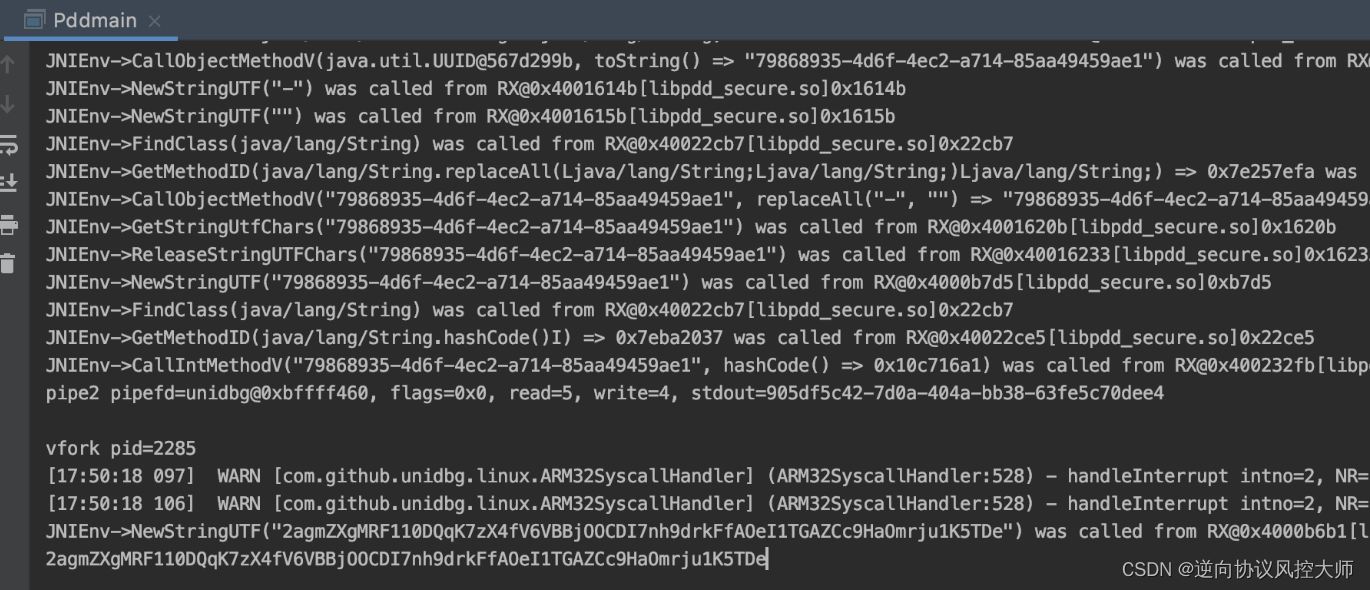
拼多多anti-token分析
前言:拼多多charles抓包分析发现跟商品相关的请求头里都带了一个anti-token的字段且每次都不一样,那么下面的操作就从分析anti-token开始了 1.jadx反编译直接搜索 选中跟http相关的类对这个方法进行打印堆栈 结合堆栈方法调用的情况找到具体anti-token是由拦截器类f…...
基于微信小程序的中医体质辨识文体活动的设计与实现(Java+spring boot+MySQL)
获取源码或者论文请私信博主 演示视频: 基于微信小程序的中医体质辨识文体活动的设计与实现(Javaspring bootMySQL) 使用技术: 前端:html css javascript jQuery ajax thymeleaf 微信小程序 后端:Java s…...
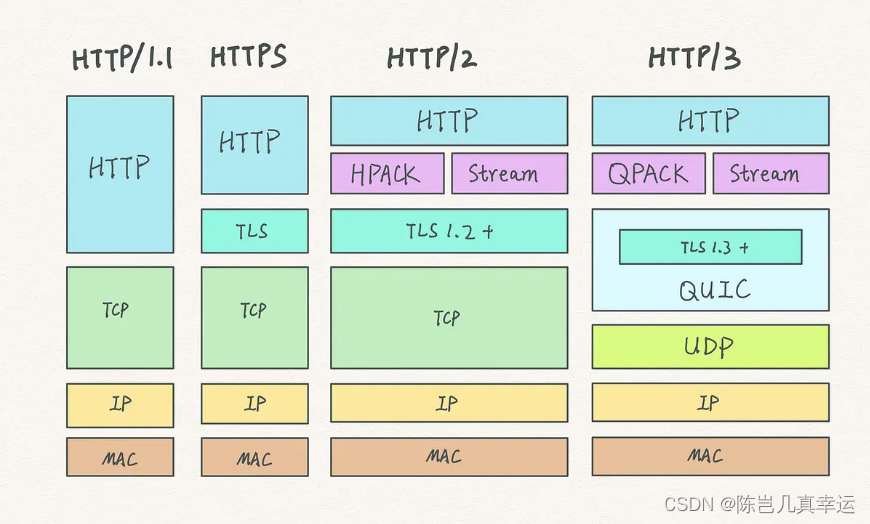
4.16 TCP 协议有什么缺陷?
目录 升级 TCP 的工作很困难 TCP 建立连接的延迟 TCP 存在队头阻塞问题 网络迁移需要重新建立 TCP 连接 升级 TCP 的工作很困难;TCP 建立连接的延迟;TCP 存在队头阻塞问题;网络迁移需要重新建立 TCP 连接; 升级 TCP 的工作很…...
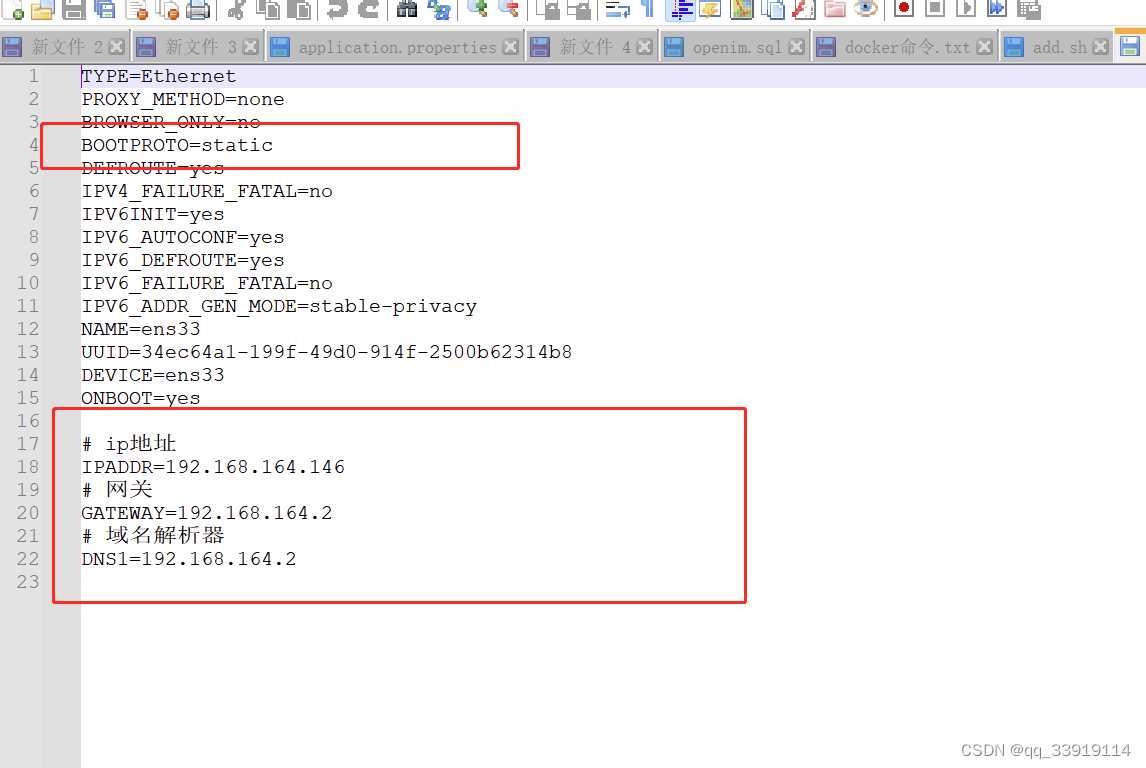
VMware 修改ip地址 虚拟机静态ip设置 centos动态ip修改为静态ip地址 centos静态ip地址 vmware修改ip地址
虚拟机的centos服务器经常变换ip,测试起来有些麻烦,故将动态ip修改为静态ip 1. 查看vmware 虚拟机网络配置: 点击编辑,打开虚拟网络配置 2. 选中nat模式,点击nat设置,最终获取网关ip: 192.168.164.2 3. 进…...

Deepin添加Ubuntu源
升级Deepin V23后,无法安装Zeal了,后面发现可以通过ubuntu源来安装。参考了以下两个文档。 添加Ubuntu源1 添加Ubuntu源2 1.添加ubuntu.list sudo vim /etc/apt/sources.list.d/ubuntu.list 2.添加中科大Ubuntu源 deb http://mirrors.ustc.edu.cn/…...

Mysql的多表查询和索引
MySQL 多表查询 当两个表查询时,从第一张表中取出一行和第二张表的每一行进行组合 返回结果含有两张表的所有列,一共返回的记录数第一张表行数*第二张表的行数(笛卡尔积) -- ?显示雇员名,雇员工资及所在部门的名字 【笛卡尔集…...

Java设计模式之建造者模式
建造者模式,又称生成器模式:将一个复杂的构建与其表示相分离,使得同样的构建过程可以创建不同的表示。 三个角色:建造者、具体的建造者、监工、使用者 建造者角色:定义生成实例所需要的所有方法; 具体的建…...
H5商城公众号商城系统源码 积分兑换商城系统独立后台
网购商城系统源码 积分兑换商城系统源码 独立后台附教程 测试环境:NginxPHP7.0MySQL5.6thinkphp伪静态...

华为OD机试 - 完全数计算(Java 2023 B卷 100分)
目录 专栏导读一、题目描述二、输入描述三、输出描述四、Java算法源码五、效果展示六、纵览全局 华为OD机试 2023B卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试(JAVA)真题(A卷B卷)》。 刷的越多&…...

每日一学——Vlan配置
VLAN(Virtual Local Area Network)是虚拟局域网的缩写,它是一种将多台主机和网络设备逻辑上划分成不同的局域网的技术。VLAN的实施可以基于端口、MAC地址、协议等多种方式进行。 VLAN的主要功能包括: 分割网络:VLAN可…...

Pimpl模式
写在前面 Pimpl(Pointer to implementation,又称作“编译防火墙”) 是一种减少代码依赖和编译时间的C编程技巧,其基本思想是将一个外部可见类(visible class)的实现细节(一般是所有私有的非虚成员)放在一个单独的实现类(implemen…...
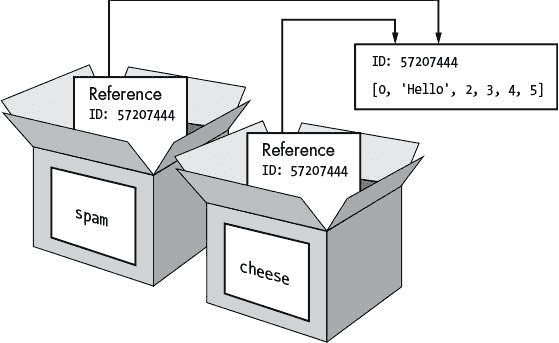
Python 密码破解指南:5~9
协议:CC BY-NC-SA 4.0 译者:飞龙 本文来自【OpenDocCN 饱和式翻译计划】,采用译后编辑(MTPE)流程来尽可能提升效率。 收割 SB 的人会被 SB 们封神,试图唤醒 SB 的人是 SB 眼中的 SB。——SB 第三定律 五、凯…...

ARM驱动开发
驱动 以来内核编译,依赖内核执行 驱动可以同时执行多份代码 没main 驱动是依赖内核的框架和操作硬件的过程 一,Linux系统组成 app: [0-3G] ---------------------------------系统调用(软中断…...

Matlab图像处理-加法运算
加法运算 图像加法运算的一个应用是将一幅图像的内容叠加到另一幅图像上,生成叠加图像效果,或给图像中每个像素叠加常数改变图像的亮度。 在MATLAB图像处理工具箱中提供的函数imadd()可实现两幅图像的相加或者一幅图像和常量的相加。 程序代码 I1 i…...
Docker容器学习:搭建自己专属的LAMP环境
目录 编写Dockerfile 1.文件内容需求: 2.值得注意的是centos6官方源已下线,所以需要切换centos-vault源! 3.Dockerfile内容 4.进入到 lamp 开始构建镜像 推送镜像到私有仓库 1.把要上传的镜像打上合适的标签 2.登录harbor仓库 3.上传镜…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
