android nv21 转 yuv420sp
上面两个函数的目标都是将NV21格式的数据转换为YUV420P格式,但是它们在处理U和V分量的方式上有所不同。
在第一个函数NV21toYUV420P_1中,U和V分量的处理方式是这样的:对于U分量,它从NV21数据的Y分量之后的每个奇数位置取数据;对于V分量,它从NV21数据的Y分量之后的每个偶数位置取数据。
而在第二个函数NV21toYUV420P中,U和V分量的处理方式是这样的:对于U分量,它从NV21数据的Y分量之后的每个偶数位置取数据;对于V分量,它从NV21数据的Y分量之后的每个奇数位置取数据。
因此,这两个函数并不完全相同。如果你的NV21数据是标准的,即V和U分量是交错存储的(首先是V,然后是U),那么你应该使用第二个函数NV21toYUV420P。
private byte[] NV21toYUV420P_1(byte[] nv21, int width, int height) {
byte[] yuv420p = new byte[widthheight3/2];
int i, j;
int ySize = width * height;// 拷贝Y分量System.arraycopy(nv21, 0, yuv420p, 0, ySize);// 处理并拷贝U分量for (i = 0; i < ySize/4; i++) {yuv420p[ySize + i] = nv21[ySize + 2 * i + 1];}// 处理并拷贝V分量for (j = 0; j < ySize/4; j++) {yuv420p[ySize + i + j] = nv21[ySize + 2 * j];}return yuv420p;
}public static byte[] NV21toYUV420P(byte[] nv21, int width, int height) {byte[] yuv420p = new byte[width*height*3/2];int i, j;int ySize = width * height;// Copy YSystem.arraycopy(nv21, 0, yuv420p, 0, ySize);// Copy U and Vfor (i = 0; i < ySize/2; i += 2) {yuv420p[ySize + i/2] = nv21[ySize + i]; // Uyuv420p[ySize + ySize/4 + i/2] = nv21[ySize + i + 1]; // V}return yuv420p;
}相关文章:

android nv21 转 yuv420sp
上面两个函数的目标都是将NV21格式的数据转换为YUV420P格式,但是它们在处理U和V分量的方式上有所不同。 在第一个函数NV21toYUV420P_1中,U和V分量的处理方式是这样的:对于U分量,它从NV21数据的Y分量之后的每个奇数位置取数据&…...

使用Nacos与Spring Boot实现配置管理
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
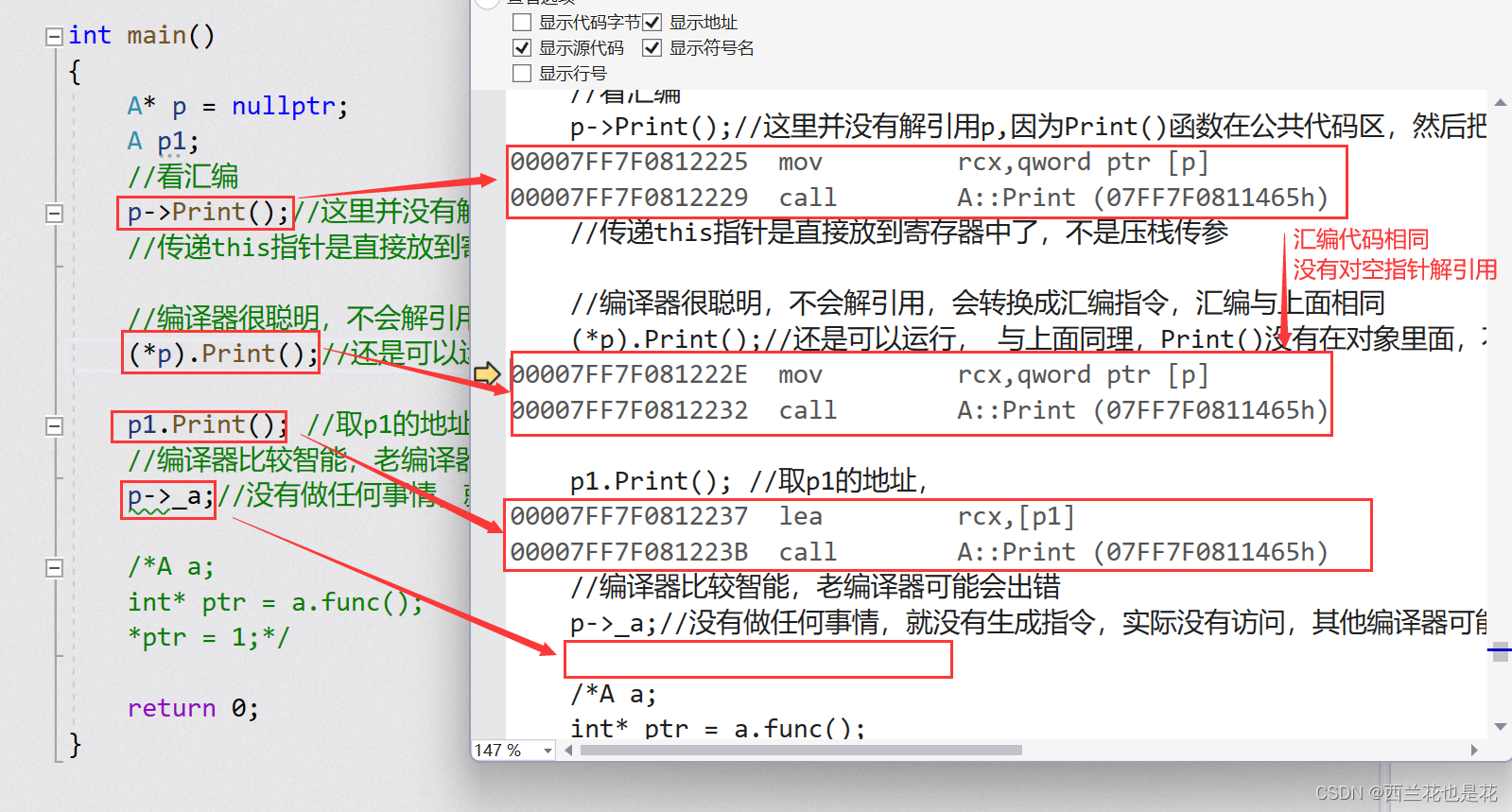
初识【类和对象】
目录 1.面向过程和面向对象初步认识 2.类的引入 3.类的定义 4.类的访问限定符及封装 5.类的作用域 6.类的实例化 7.类的对象大小的计算 8.类成员函数的this指针 1.面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题的…...

软考高级系统架构设计师系列论文八十六:论企业应用集成
软考高级系统架构设计师系列论文八十六:论企业应用集成 一、企业应用集成相关知识点二、摘要三、正文四、总结一、企业应用集成相关知识点 软考高级系统架构设计师系列之:企业集成平台技术的应用和架构设计二、摘要 2022年10月,我参加了***车站综合信息平台项目的开发,承…...

HarmonyOS ArkUI 属性动画入门详解
HarmonyOS ArkUI 属性动画入门详解 前言属性动画是什么?我们借助官方的话来说,我们自己简单归纳下 参数解释举个例子旋转动画 位移动画组合动画总结 前言 鸿蒙OS最近吹的很凶,赶紧卷一下。学习过程中发现很多人吐槽官方属性动画这一章比较敷…...
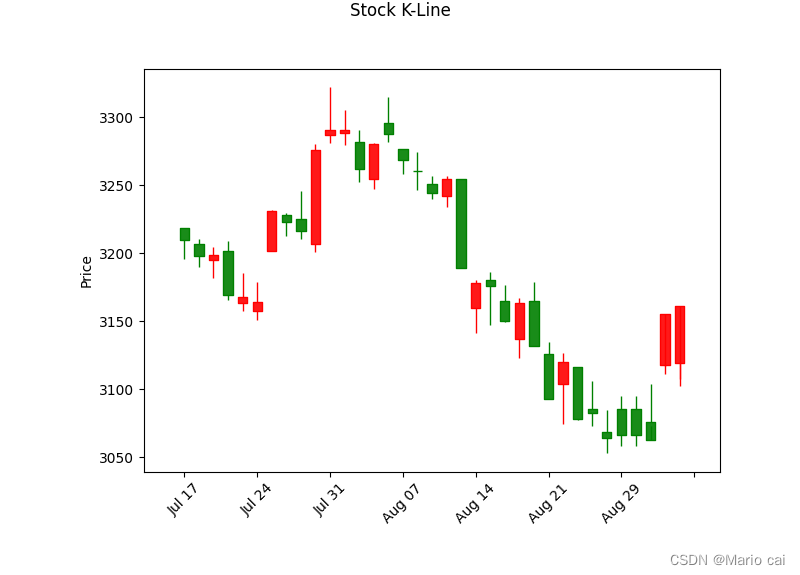
基于XGBoots预测A股大盘《上证指数》(代码+数据+一键可运行)
对AI炒股感兴趣的小伙伴可加WX:caihaihua057200(备注:学校/公司名字方向) 另外我还有些AI的应用可以一起研究(我一直开源代码) 1、引言 在这期内容中,我们回到AI预测股票,转而探索…...

5G NR:PRACH频域资源
PRACH在频域位置由IE RACH-ConfigGeneric中参数msg1-FrequencyStart和msg1-FDM所指示,其中, msg1-FrequencyStart确定PRACH occasion 0的RB其实位置相对于上行公共BWP的频域其实位置(即BWP 0)的偏移,即确定PRACH的频域起始位置msg1-FDM的取值…...
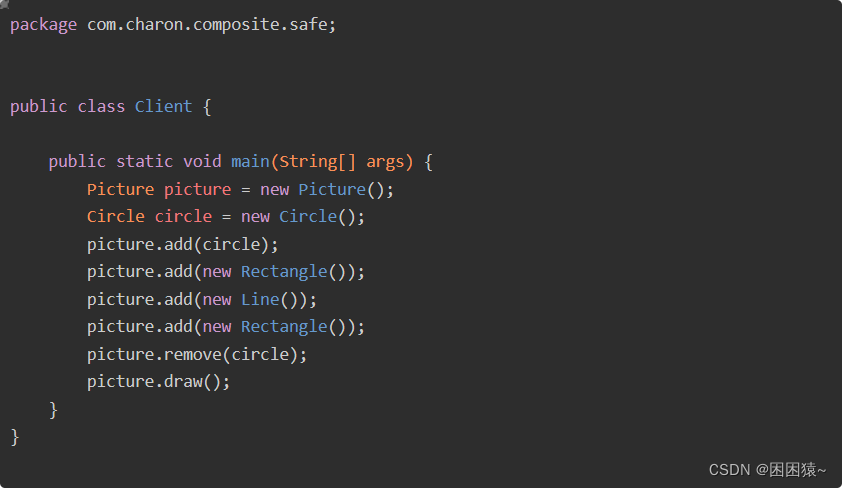
设计模式——组合模式
什么是组合模式 组合模式(Composite Pattern):组合多个对象形成树形结构以表示具有“整体—部分”关系的层次结构。组合模式对单个对象(即叶子对象)和组合对象(即容器对象)的使用具有一致性,组合模式又可以…...

get属性是什么?有什么用?在什么场景用?get会被Json序列化?
在JavaScript中,对象的属性不仅可以是数据属性(即常规的键值对),还可以是访问器属性(accessor properties)。访问器属性不包含实际的数据值,而是定义了如何获取(get)和设…...

这可能是你看过最详细的 [八大排序算法]
排序算法 前置知识 [排序稳定性]一、直接插入排序二、希尔排序三、直接选择排序四、堆排序五、冒泡排序六、快速排序七、归并排序八、计数排序(非比较排序)排序复杂度和稳定性总结 前置知识 [排序稳定性] 假定在待排序的记录序列中,存在多个…...

docker的安装
CentOS7 安装 Docker 安装需要的软件包, yum-util 提供yum-config-manager功能,另两个是devicemapper驱动依赖 yum install -y yum-utils device-mapper-persistent-data lvm2 添加下载源 yum-config-manager --add-repo http://mirrors.aliyun.com/…...
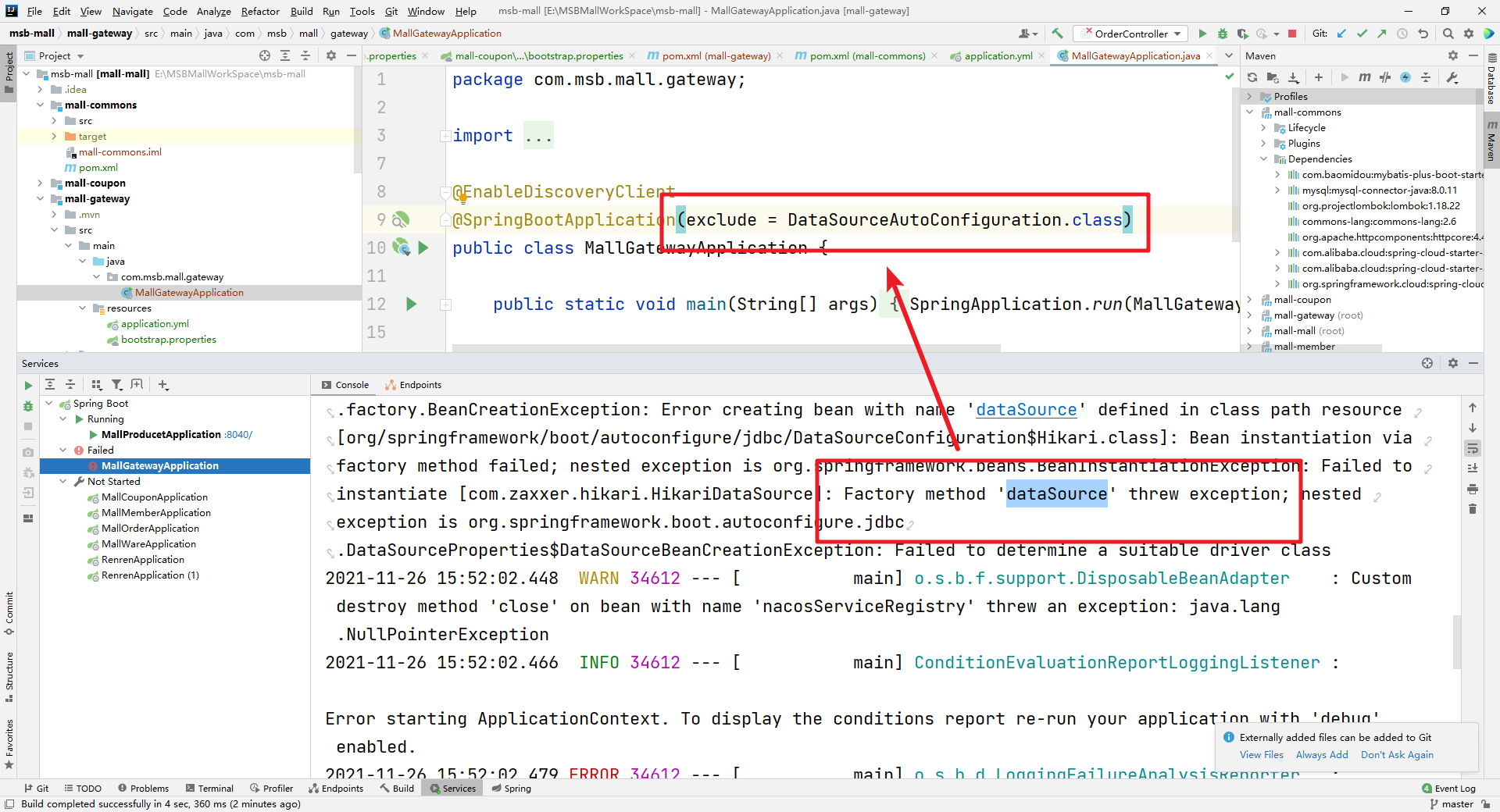
【业务功能篇75】微服务项目环境搭建docker-mysql-redisSpringCloudAlibaba
项目环境准备 1.虚拟机环境 我们可以通过VMWare来安装,但是通过VMWare安装大家经常会碰到网络ip连接问题,为了减少额外的环境因素影响,Docker内容的讲解我们会通过VirtualBox结合Vagrant来安装虚拟机。 VirtualBox官网:https:/…...
学习笔记|认识数码管|控制原理|数码管实现0-9的显示|段码跟位码|STC32G单片机视频开发教程(冲哥)|第九集:数码管静态显示
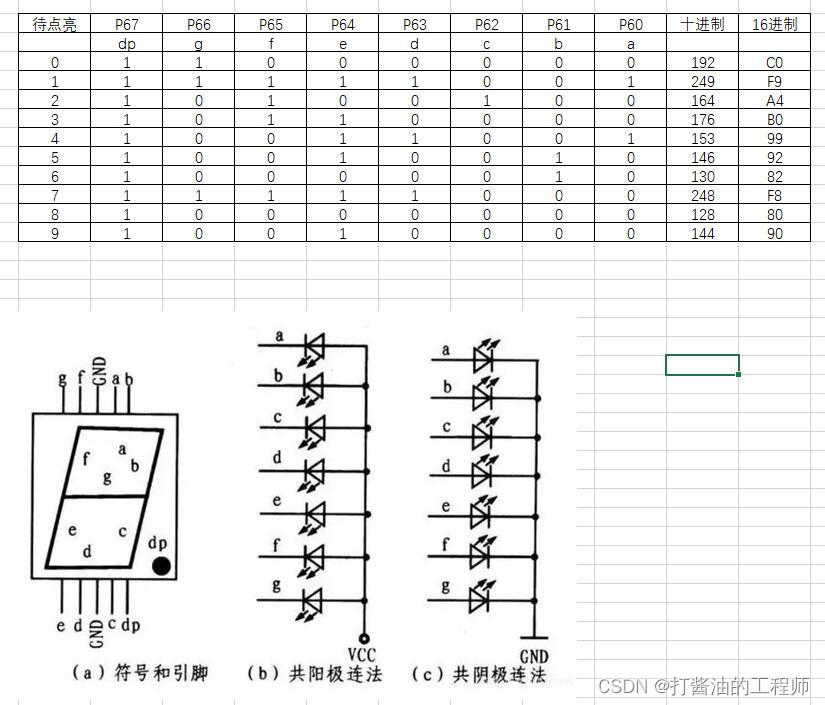
文章目录 1.认识数码管2.控制原理十进制转换为任意进制其它进制转十进制 3.数码管实现0-9的显示1.用数组定义0-9的内码段码跟位码的区别2.尝试用延时实现0-9的循环显示3.用按键控制数字的加或者减。 总结课后练习: 1.认识数码管 数码管按段数可分为七段数码管和八段…...

CentOS 7/8 firewall 转发端口
#开启系统路由模式功能 echo net.ipv4.ip_forward1>>/etc/sysctl.conf sysctl -p #开启firewalld systemctl start firewalld 打开防火墙伪装IP # 检查是否允许伪装IP,返回no表示没开启,反之开启伪装IP firewall-cmd --query-masquerade #设置…...

mysql自动备份脚本
备份脚本 #!/bin/bash #author cheng #mysql数据自动备份 mysql_user“root” mysql_password“passwprd” mysql_host“localhost” mysql_port“3306” mysql_charset“utf8mb4” #备份文件存放地址(根据实际情况填写) backup_location/usr/cheng/msg_manager/sql #是否删…...
VUE笔记(九)vuex
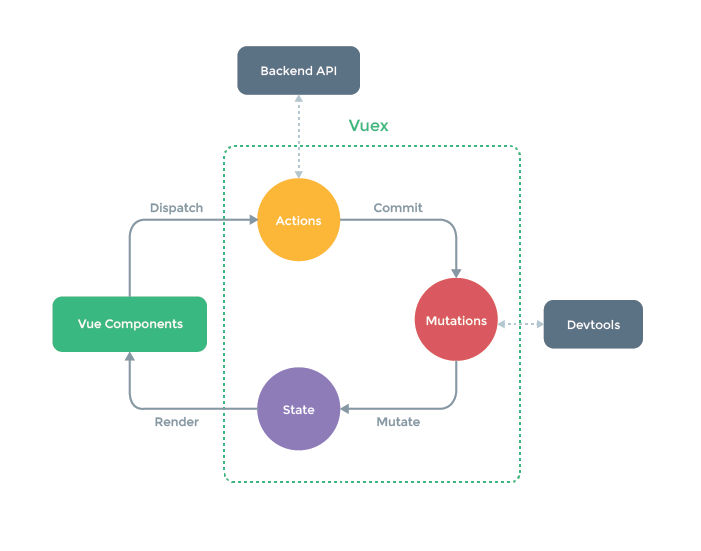
一、vuex的简介 1、回顾组件之间的通讯 父组件向子组件通讯:通过props实现 子组件向父组件通讯:通过自定义事件($emit)方式来实现 兄弟组件之间的通讯:事件总线($eventBus)、订阅与发布方式来实现 跨级组件的通讯…...

Webpack高频面试题
Webpack高频面试题 1 谈谈你对webpack的看法 现在的前端网页功能丰富,特别是SPA(single page web application 单页应用)技术流行后,JavaScript的复杂度增加和需要一大堆依赖包,还需要解决Scss,Less……新…...
数字基带传输系统
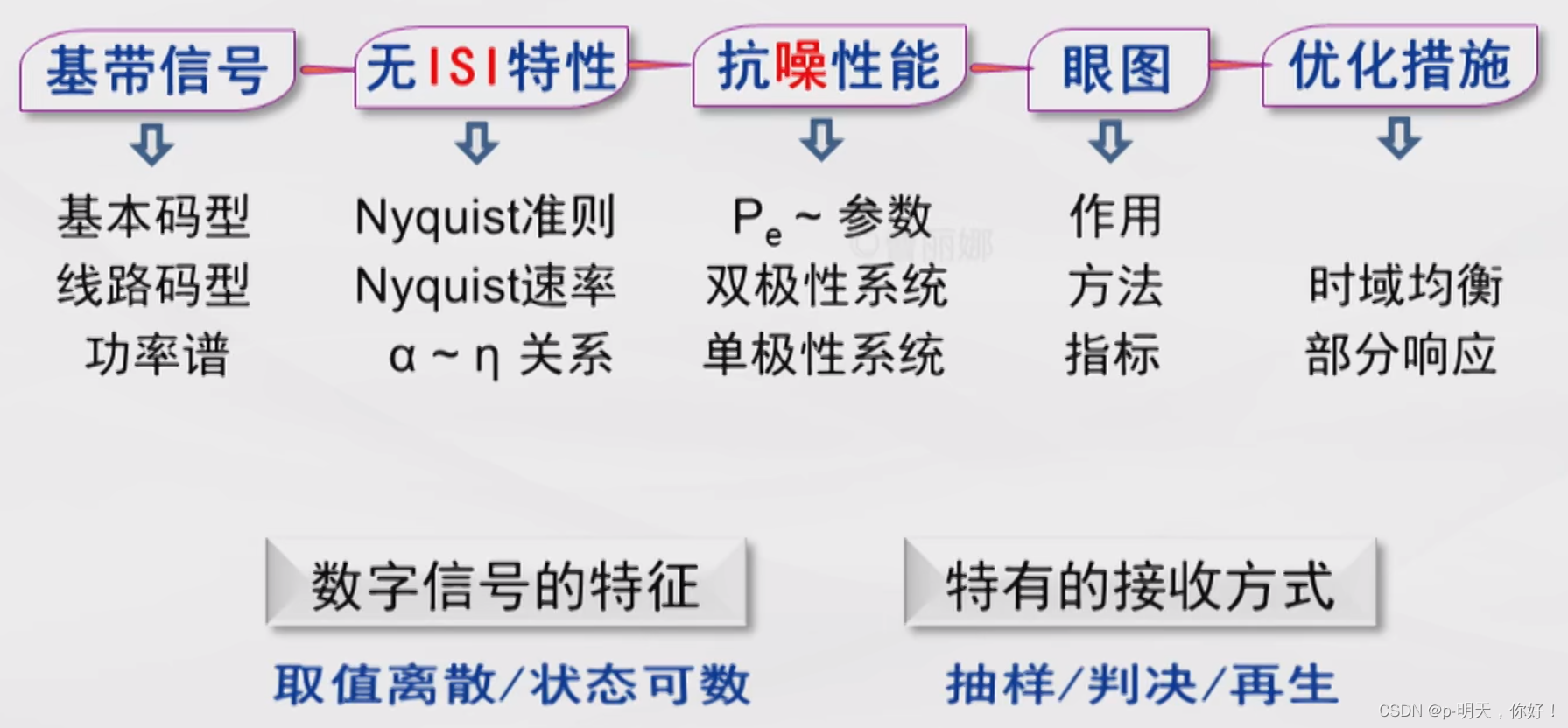
文章目录 前言一、数字基带系统基本组成二、基本码型1、数字基带信号2、6 种基本码型 三、数字基带信号的频谱特性四、数字基带信号选码1、原则2、常用的传输码型①、AMI 码(传号交替反转码)②、 H D B 3 HDB_3 HDB3 码(3 阶高密度双极性码…...
FPGA使用MIG调用SODIMM内存条接口教程,提供vivado工程源码和技术支持
目录 1、前言免责声明 2、SODIMM内存条简介3、设计思路框架视频输入视频缓存MIG配置调用SODIMM内存条VGA时序视频输出 4、vivado工程详解5、上板调试验证6、福利:工程代码的获取 1、前言 FPGA应用中,数据缓存是一大重点,不管是图像处理还是A…...

深度学习数据预处理
参考文章:深度学习中的数据预处理方法总结 在深度学习中,数据预处理(preprocessing)的重要性体现在以下几个方面: 1、数据质量: 原始数据通常包含错误、缺失值、异常值和噪声。预处理能够检测和处理这些问…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
