【KMP算法-代码随想录】
目录
- 1.什么是KMP
- 2.什么是next数组
- 3.什么是前缀表
- (1)前后缀含义
- (2)最长公共前后缀
- (3)前缀表的必要性
- 4.计算前缀表
- 5.前缀表与next数组
- (1)使用next数组来匹配
- 6.构造next数组
- (1)初始化
- (2)处理前后缀不相同的情况
- (3)处理前后缀相同的情况
- 4.前缀表(不减一)C++实现
- 7.使用next数组来做匹配
- (1)前缀表统一减一
- (2)不减一的整体实现
1.什么是KMP
说到KMP,先说一下KMP这个名字是怎么来的,为什么叫做KMP呢。
因为是由这三位学者发明的:Knuth,Morris和Pratt,所以取了三位学者名字的首字母。所以叫做KMP。
KMP(Knuth-Morris-Pratt)算法是一种字符串匹配算法,用于在一个主文本字符串中查找一个模式字符串的出现位置。它的核心思想是避免在匹配过程中反复回溯主文本中的位置,从而提高匹配效率。
2.什么是next数组
next数组也称为部分匹配表(Partial Match Table),是KMP算法中的一种预处理技术,用于存储模式字符串中每个位置的最长匹配前缀子串的结尾位置。
具体来说,next数组的每个元素代表着模式字符串中对应位置的最长匹配前缀子串的结尾位置。通过构建next数组,我们可以在匹配过程中根据当前不匹配字符的位置,快速确定模式字符串的指针移动的位置,从而实现高效的字符串匹配。
3.什么是前缀表
1.在字符串匹配算法中,前缀表(Prefix Table)也被称为部分匹配表(Partial Match Table)或next数组。它是用于KMP算法中的核心数据结构之一,用于存储模式字符串中每个位置的最长匹配前缀子串的结尾位置。
2.前缀表是用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
为了清楚地了解前缀表的来历,我们来举一个例子:
要在文本串:aabaabaafa 中查找是否出现过一个模式串:aabaaf
。
可以看出,文本串中第六个字符b 和 模式串的第六个字符f,不匹配了。如果暴力匹配,发现不匹配,此时就要从头匹配了。
但如果使用前缀表,就不会从头匹配,而是从上次已经匹配的内容开始匹配,找到了模式串中第三个字符b继续开始匹配。
此时就要问了前缀表是如何记录的呢?
首先要知道前缀表的任务是当前位置匹配失败,找到之前已经匹配上的位置,再重新匹配,此也意味着在某个字符失配时,前缀表会告诉你下一步匹配中,模式串应该跳到哪个位置。
那么什么是前缀表:记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
(在上述例子中前缀和后缀就分别为模式串中b前后的aa)
(1)前后缀含义
前缀:不包含最后一个字符的所有以第一个字符开头的连续子串。
后缀:不包含第一个字符的所有以最后一个字符结尾的连续子串。
(2)最长公共前后缀
最长公共前后缀就是在字符串某个位置前面的子串和后面的子串中相同的最长长度。例如,对于字符串 “abcabc”,最长公共前后缀的长度为3,因为 “abc” 既是最长的前缀,也是最长的后缀。
(3)前缀表的必要性
刚刚匹配的过程在下标5的地方遇到不匹配,模式串是指向f,如图:

然后就找到了下标2,指向b,继续匹配:如图:

能告诉我们上次匹配的位置,并跳过去
下标5之前这部分的字符串(也就是字符串aabaa)的最长相等的前缀和后缀字符串是子字符串aa ,因为找到了最长相等的前缀和后缀,匹配失败的位置是后缀子串的后面,那么我们找到与其相同的前缀的后面重新匹配就可以了。
4.计算前缀表
如图:

长度为前1个字符的子串a,最长相同前后缀的长度为0。

长度为前2个字符的子串aa,最长相同前后缀的长度为1。

长度为前3个字符的子串aab,最长相同前后缀的长度为0。
以此类推:长度为前4个字符的子串aaba,最长相同前后缀的长度为1。 长度为前5个字符的子串aabaa,最长相同前后缀的长度为2。 长度为前6个字符的子串aabaaf,最长相同前后缀的长度为0。

下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示:

找到的不匹配的位置, 那么此时我们要看它的前一个字符的前缀表的数值是多少。
为什么要前一个字符的前缀表的数值呢,因为要找前面字符串的最长相同的前缀和后缀。
所以要看前一位的 前缀表的数值。
前一个字符的前缀表的数值是2, 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
最后就在文本串中找到了和模式串匹配的子串了。
5.前缀表与next数组
很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
为什么这么做呢,其实也是很多文章视频没有解释清楚的地方。
其实这并不涉及到KMP的原理,而是具体实现,next数组既可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。
(1)使用next数组来匹配
以下我们以前缀表统一减一之后的next数组来做演示。
有了next数组,就可以根据next数组来 匹配文本串s,和模式串t了。
注意next数组是新前缀表(旧前缀表统一减一了)。
匹配过程动画如下:

两种情况:
1.总体往后移,到哪一位不匹配,就直接找那一位的下标
2.如果在其基础上减去一,则是找他前一位的下标+1即可
6.构造next数组
我们定义一个函数getNext来构建next数组,函数参数为指向next数组的指针,和一个字符串。 代码如下:
void getNext(int* next, const string& s)
构造next数组其实就是计算模式串s,前缀表的过程。 主要有如下三步:
(1)初始化
定义两个指针i和j,j指向前缀末尾位置,i指向后缀末尾位置。
然后还要对next数组进行初始化赋值,如下:
int j = -1;
next[0] = j;
next[i] 表示 i(包括i)之前最长相等的前后缀长度(其实就是j)
所以初始化next[0] = j 。
(2)处理前后缀不相同的情况
因为j初始化为-1,那么i就从1开始,进行s[i] 与 s[j+1]的比较。
所以遍历模式串s的循环下标i 要从 1开始,代码如下:
for (int i = 1; i < s.size(); i++) {
next数组的回退操作是为了利用已经计算得到的信息,调整模式字符串的指针位置,以避免不必要的字符比较,提高KMP算法的匹配效率。
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了j = next[j]; // 向前回退
}
(3)处理前后缀相同的情况
如果 s[i] 与 s[j + 1] 相同,那么就同时向后移动i 和j 说明找到了相同的前后缀,同时还要将j(前缀的长度)赋给next[i], 因为next[i]要记录相同前后缀的长度。
if (s[i] == s[j + 1]) { // 找到相同的前后缀j++;
}
next[i] = j;
最后整体构建next数组的函数代码如下:
void getNext(int* next, const string& s){int j = -1;next[0] = j;for(int i = 1; i < s.size(); i++) { // 注意i从1开始while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了j = next[j]; // 向前回退}if (s[i] == s[j + 1]) { // 找到相同的前后缀j++;}next[i] = j; // 将j(前缀的长度)赋给next[i]}
}
如下为next数组的流程图

4.前缀表(不减一)C++实现
void getNext(int* next, const string& s) {int j = 0;next[0] = 0;for(int i = 1; i < s.size(); i++) {while (j > 0 && s[i] != s[j]) { // j要保证大于0,因为下面有取j-1作为数组下标的操作j = next[j - 1]; // 注意这里,是要找前一位的对应的回退位置了}if (s[i] == s[j]) {j++;}next[i] = j;}}
7.使用next数组来做匹配
i就从0开始,遍历文本串,代码如下:
for (int i = 0; i < s.size(); i++)
接下来就是 s[i] 与 t[j + 1] (因为j从-1开始的) 进行比较。
如果 s[i] 与 t[j + 1] 不相同,j就要从next数组里寻找下一个匹配的位置。
代码如下:
while(j >= 0 && s[i] != t[j + 1]) {j = next[j];
}
如果 s[i] 与 t[j + 1] 相同,那么i 和 j 同时向后移动, 代码如下:
if (s[i] == t[j + 1]) {j++; // i的增加在for循环里
}
本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始),所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度,就是文本串字符串中出现模式串的第一个位置。
if (j == (t.size() - 1) ) {return (i - t.size() + 1);
}
那么使用next数组,用模式串匹配文本串的整体代码如下:
int j = -1; // 因为next数组里记录的起始位置为-1
for (int i = 0; i < s.size(); i++) { // 注意i就从0开始while(j >= 0 && s[i] != t[j + 1]) { // 不匹配j = next[j]; // j 寻找之前匹配的位置}if (s[i] == t[j + 1]) { // 匹配,j和i同时向后移动j++; // i的增加在for循环里}if (j == (t.size() - 1) ) { // 文本串s里出现了模式串treturn (i - t.size() + 1);}
}
(1)前缀表统一减一
class Solution {
public:void getNext(int* next, const string& s) {int j = -1;next[0] = j;for(int i = 1; i < s.size(); i++) { // 注意i从1开始while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了j = next[j]; // 向前回退}if (s[i] == s[j + 1]) { // 找到相同的前后缀j++;}next[i] = j; // 将j(前缀的长度)赋给next[i]}}int strStr(string haystack, string needle) {if (needle.size() == 0) {return 0;}int next[needle.size()];getNext(next, needle);int j = -1; // // 因为next数组里记录的起始位置为-1for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配j = next[j]; // j 寻找之前匹配的位置}if (haystack[i] == needle[j + 1]) { // 匹配,j和i同时向后移动j++; // i的增加在for循环里}if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串treturn (i - needle.size() + 1);}}return -1;}
};
(2)不减一的整体实现
class Solution {
public:void getNext(int* next, const string& s) {int j = 0;next[0] = 0;for(int i = 1; i < s.size(); i++) {while (j > 0 && s[i] != s[j]) {j = next[j - 1];}if (s[i] == s[j]) {j++;}next[i] = j;}}int strStr(string haystack, string needle) {if (needle.size() == 0) {return 0;}int next[needle.size()];getNext(next, needle);int j = 0;for (int i = 0; i < haystack.size(); i++) {while(j > 0 && haystack[i] != needle[j]) {j = next[j - 1];}if (haystack[i] == needle[j]) {j++;}if (j == needle.size() ) {return (i - needle.size() + 1);}}return -1;}
};
相关文章:

【KMP算法-代码随想录】
目录 1.什么是KMP2.什么是next数组3.什么是前缀表(1)前后缀含义(2)最长公共前后缀(3)前缀表的必要性 4.计算前缀表5.前缀表与next数组(1)使用next数组来匹配 6.构造next数组…...
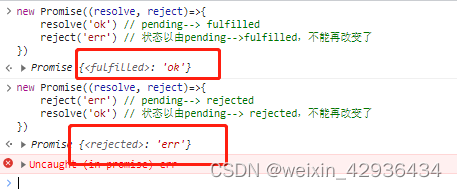
【手写promise——基本功能、链式调用、promise.all、promise.race】
文章目录 前言一、前置知识二、实现基本功能二、实现链式调用三、实现Promise.all四、实现Promise.race总结 前言 关于动机,无论是在工作还是面试中,都会遇到Promise的相关使用和原理,手写Promise也有助于学习设计模式以及代码设计。 本文主…...
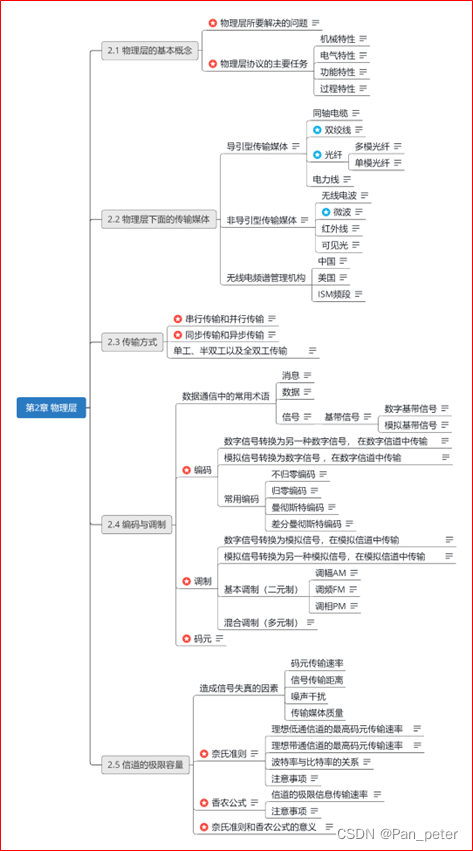
计算机网络-笔记-第二章-物理层
目录 二、第二章——物理层 1、物理层的基本概念 2、物理层下面的传输媒体 (1)光纤、同轴电缆、双绞线、电力线【导引型】 (2)无线电波、微波、红外线、可见光【非导引型】 (3)无线电【频谱的使用】 …...

前端开发中的单伪标签清除和双伪标签清除
引言 在前端开发中,我们经常会遇到一些样式上的问题,其中之一就是伪元素造成的布局问题。为了解决这个问题,我们可以使用伪标签清除技术。本篇博客将介绍单伪标签清除和双伪标签清除的概念、用法和示例代码,并详细解释它们的原理…...

云计算中的数据安全与隐私保护策略
文章目录 1. 云计算中的数据安全挑战1.1 数据泄露和数据风险1.2 多租户环境下的隔离问题 2. 隐私保护策略2.1 数据加密2.2 访问控制和身份验证 3. 应对方法与技术3.1 零知识证明(Zero-Knowledge Proofs)3.2 同态加密(Homomorphic Encryption&…...
MacOS软件安装包分享(附安装教程)
目录 一、软件简介 二、软件下载 一、软件简介 MacOS是一种由苹果公司开发的操作系统,专门用于苹果公司的计算机硬件。它被广泛用于创意和专业应用程序,如图像设计、音频和视频编辑等。以下是关于MacOS的详细介绍。 1、MacOS的历史和演变 MacOS最初于…...

【linux进程概念】
目录: 冯诺依曼体系结构操作系统进程 基本概念描述进程-PCBtask_struct-PCB的一种task_ struct内容分类组织进程查看进程 fork()函数 冯诺依曼体系结构 我们常见的计算机,如笔记本。我们不常见的计算机,如服务器,大部分都遵守冯诺…...

直击成都国际车展:远航汽车多款车型登陆车展,打造完美驾乘体验
随着市场渗透率日益高涨,新能源汽车成为今年成都国际车展的关注焦点。在本届车展上,新能源品牌占比再创新高,覆盖两个展馆,印证了当下新能源汽车市场的火爆。作为大运集团重磅打造的高端品牌,远航汽车深度洞察高端智能…...

android nv21 转 yuv420sp
上面两个函数的目标都是将NV21格式的数据转换为YUV420P格式,但是它们在处理U和V分量的方式上有所不同。 在第一个函数NV21toYUV420P_1中,U和V分量的处理方式是这样的:对于U分量,它从NV21数据的Y分量之后的每个奇数位置取数据&…...

使用Nacos与Spring Boot实现配置管理
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...
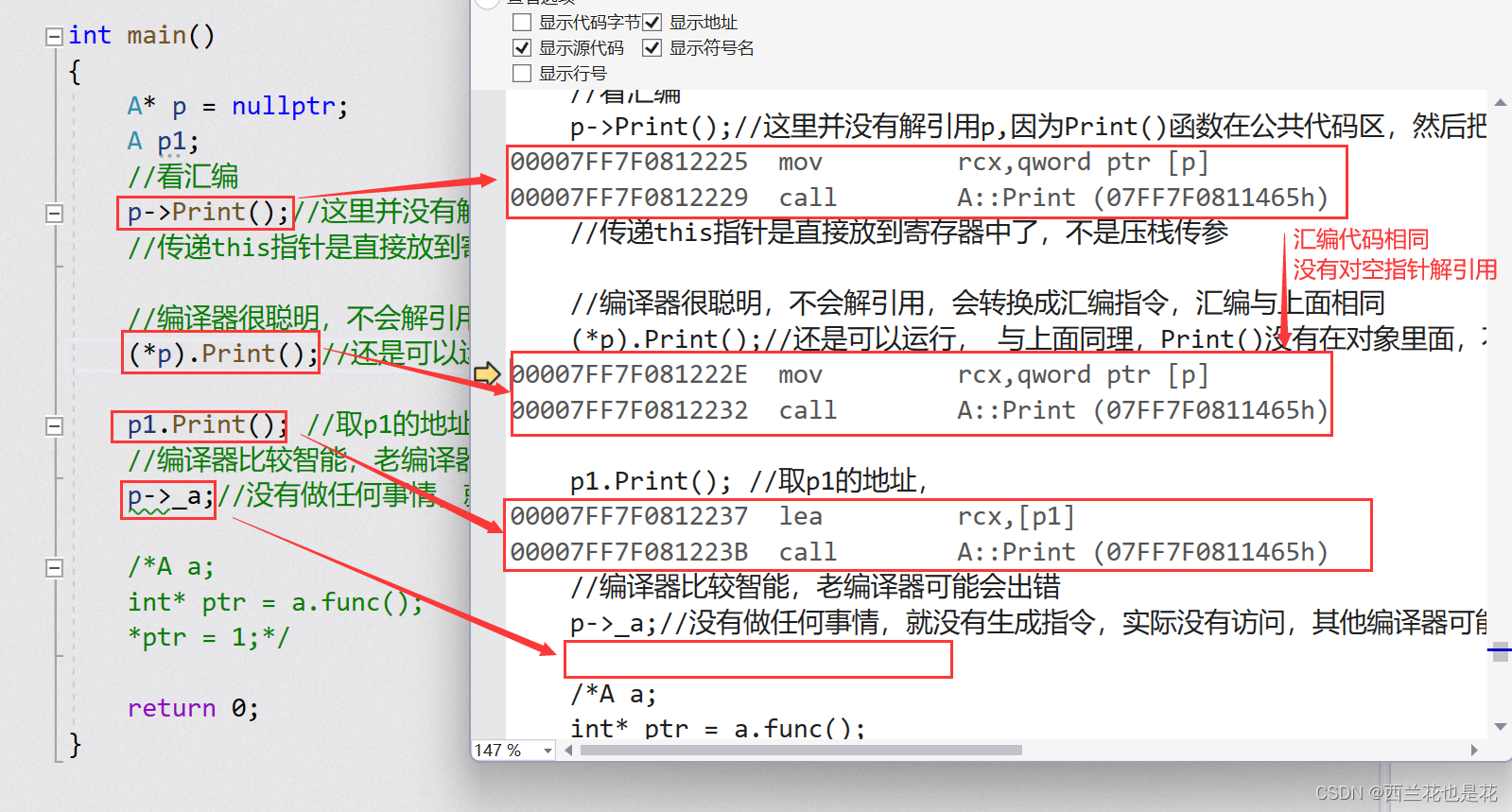
初识【类和对象】
目录 1.面向过程和面向对象初步认识 2.类的引入 3.类的定义 4.类的访问限定符及封装 5.类的作用域 6.类的实例化 7.类的对象大小的计算 8.类成员函数的this指针 1.面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题的…...

软考高级系统架构设计师系列论文八十六:论企业应用集成
软考高级系统架构设计师系列论文八十六:论企业应用集成 一、企业应用集成相关知识点二、摘要三、正文四、总结一、企业应用集成相关知识点 软考高级系统架构设计师系列之:企业集成平台技术的应用和架构设计二、摘要 2022年10月,我参加了***车站综合信息平台项目的开发,承…...

HarmonyOS ArkUI 属性动画入门详解
HarmonyOS ArkUI 属性动画入门详解 前言属性动画是什么?我们借助官方的话来说,我们自己简单归纳下 参数解释举个例子旋转动画 位移动画组合动画总结 前言 鸿蒙OS最近吹的很凶,赶紧卷一下。学习过程中发现很多人吐槽官方属性动画这一章比较敷…...
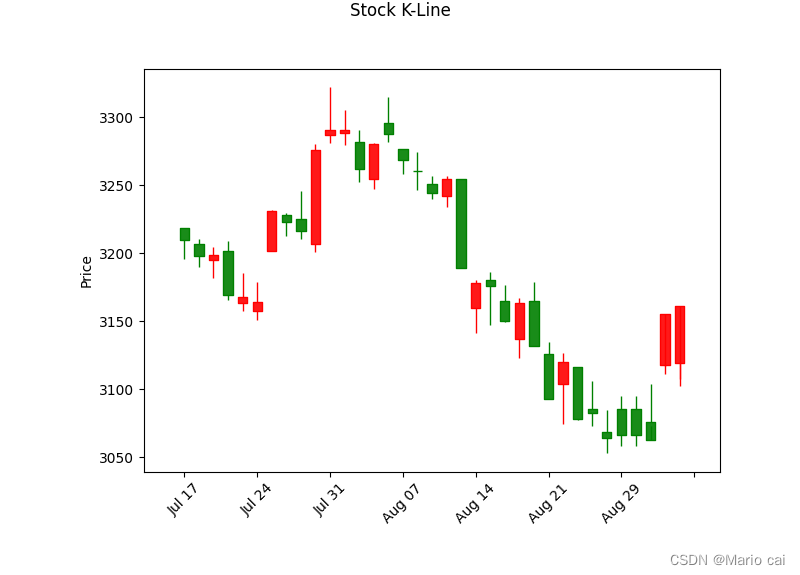
基于XGBoots预测A股大盘《上证指数》(代码+数据+一键可运行)
对AI炒股感兴趣的小伙伴可加WX:caihaihua057200(备注:学校/公司名字方向) 另外我还有些AI的应用可以一起研究(我一直开源代码) 1、引言 在这期内容中,我们回到AI预测股票,转而探索…...

5G NR:PRACH频域资源
PRACH在频域位置由IE RACH-ConfigGeneric中参数msg1-FrequencyStart和msg1-FDM所指示,其中, msg1-FrequencyStart确定PRACH occasion 0的RB其实位置相对于上行公共BWP的频域其实位置(即BWP 0)的偏移,即确定PRACH的频域起始位置msg1-FDM的取值…...
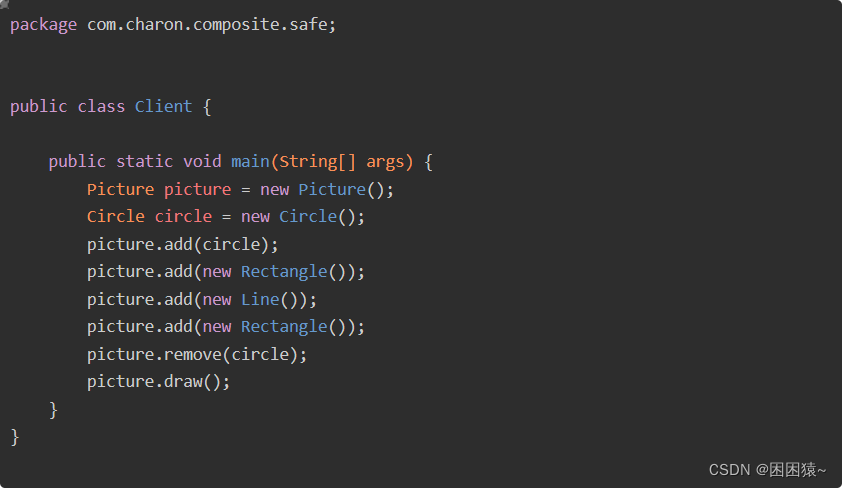
设计模式——组合模式
什么是组合模式 组合模式(Composite Pattern):组合多个对象形成树形结构以表示具有“整体—部分”关系的层次结构。组合模式对单个对象(即叶子对象)和组合对象(即容器对象)的使用具有一致性,组合模式又可以…...

get属性是什么?有什么用?在什么场景用?get会被Json序列化?
在JavaScript中,对象的属性不仅可以是数据属性(即常规的键值对),还可以是访问器属性(accessor properties)。访问器属性不包含实际的数据值,而是定义了如何获取(get)和设…...

这可能是你看过最详细的 [八大排序算法]
排序算法 前置知识 [排序稳定性]一、直接插入排序二、希尔排序三、直接选择排序四、堆排序五、冒泡排序六、快速排序七、归并排序八、计数排序(非比较排序)排序复杂度和稳定性总结 前置知识 [排序稳定性] 假定在待排序的记录序列中,存在多个…...

docker的安装
CentOS7 安装 Docker 安装需要的软件包, yum-util 提供yum-config-manager功能,另两个是devicemapper驱动依赖 yum install -y yum-utils device-mapper-persistent-data lvm2 添加下载源 yum-config-manager --add-repo http://mirrors.aliyun.com/…...
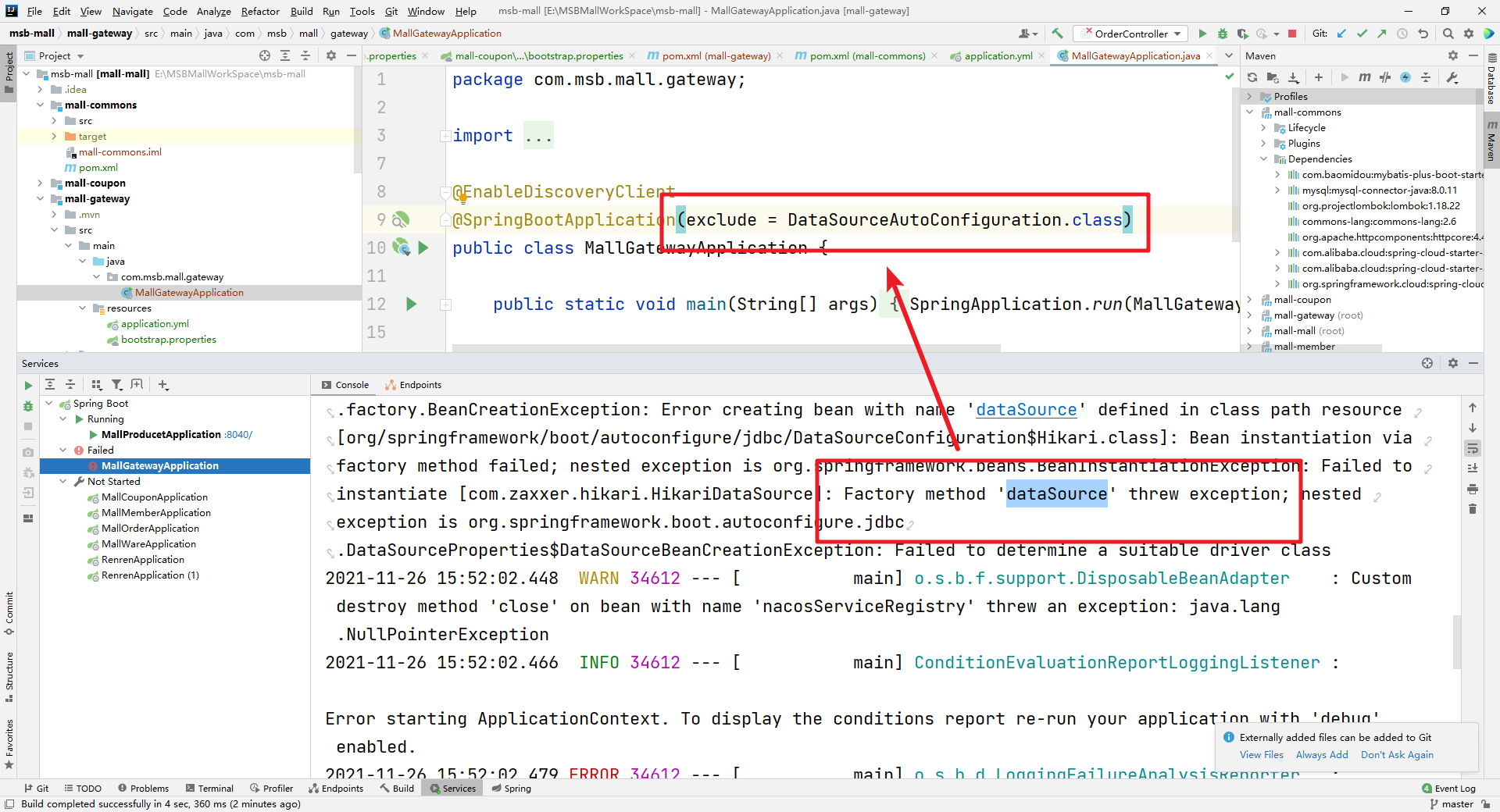
【业务功能篇75】微服务项目环境搭建docker-mysql-redisSpringCloudAlibaba
项目环境准备 1.虚拟机环境 我们可以通过VMWare来安装,但是通过VMWare安装大家经常会碰到网络ip连接问题,为了减少额外的环境因素影响,Docker内容的讲解我们会通过VirtualBox结合Vagrant来安装虚拟机。 VirtualBox官网:https:/…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...
