LeetCode 1267. 统计参与通信的服务器
【LetMeFly】1267.统计参与通信的服务器
力扣题目链接:https://leetcode.cn/problems/count-servers-that-communicate/
这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。
如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。
请你统计并返回能够与至少一台其他服务器进行通信的服务器的数量。
示例 1:
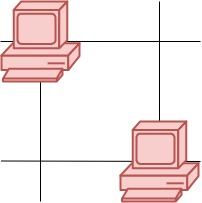
输入:grid = [[1,0],[0,1]] 输出:0 解释:没有一台服务器能与其他服务器进行通信。
示例 2:
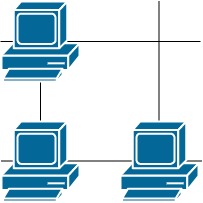
输入:grid = [[1,0],[1,1]] 输出:3 解释:所有这些服务器都至少可以与一台别的服务器进行通信。
示例 3:
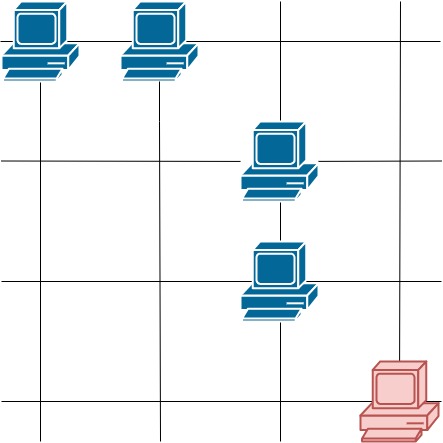
输入:grid = [[1,1,0,0],[0,0,1,0],[0,0,1,0],[0,0,0,1]] 输出:4 解释:第一行的两台服务器互相通信,第三列的两台服务器互相通信,但右下角的服务器无法与其他服务器通信。
提示:
m == grid.lengthn == grid[i].length1 <= m <= 2501 <= n <= 250grid[i][j] == 0 or 1
方法一:计数
假设 g i r d gird gird的 s i z e size size为 n × m n\times m n×m,开辟两个数组 r o w [ n ] row[n] row[n]和 c o l [ m ] col[m] col[m],分别记录某行服务器个数 和 某列的服务器个数。
遍历一遍地图矩阵 g r i d grid grid,若此处有服务器(server) 且 此行或此列不只一台服务器,则 a n s + + ans++ ans++
- 时间复杂度 O ( n × m ) O(n\times m) O(n×m)
- 空间复杂度 O ( n + m ) O(n + m) O(n+m)
AC代码
C++
class Solution {
public:int countServers(vector<vector<int>>& grid) {int n = grid.size(), m = grid[0].size();vector<int> row(n), col(m);for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {row[i] += grid[i][j], col[j] += grid[i][j];}}int ans = 0;for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {ans += grid[i][j] * (row[i] > 1 || col[j] > 1);}}return ans;}
};
Python
# from typing import Listclass Solution:def countServers(self, grid: List[List[int]]) -> int:n, m = len(grid), len(grid[0])col, row = [0] * n, [0] * mfor i in range(n):for j in range(m):col[i] += grid[i][j]row[j] += grid[i][j]ans = 0for i in range(n):for j in range(m):ans += grid[i][j] * (col[i] > 1 or row[j] > 1)return ans
同步发文于CSDN,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/132466649
相关文章:

LeetCode 1267. 统计参与通信的服务器
【LetMeFly】1267.统计参与通信的服务器 力扣题目链接:https://leetcode.cn/problems/count-servers-that-communicate/ 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表…...
)
169. 多数元素(哈希表)
169. 多数元素 给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。 你可以假设数组是非空的,并且给定的数组总是存在多数元素。 class Solution { public:int majorityElement(vector<int&…...
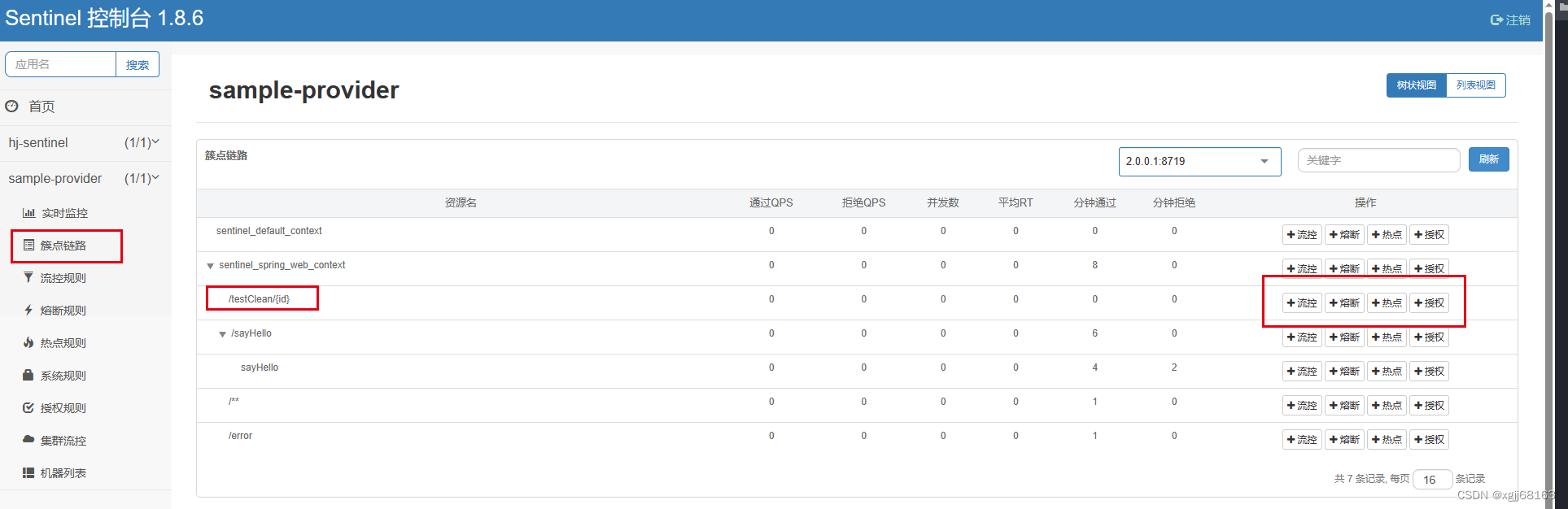
微服务集成spring cloud sentinel
目录 1. sentinel使用场景 2. sentinel组成 3. sentinel dashboard搭建 4. sentinel客户端详细使用 4.1 引入依赖 4.2 application.properties增加dashboard注册地址 4.3 手动增加限流配置类 4.4 rest接口及service类 4.5 通过dashboard动态配置限流规则 1. sentinel使…...
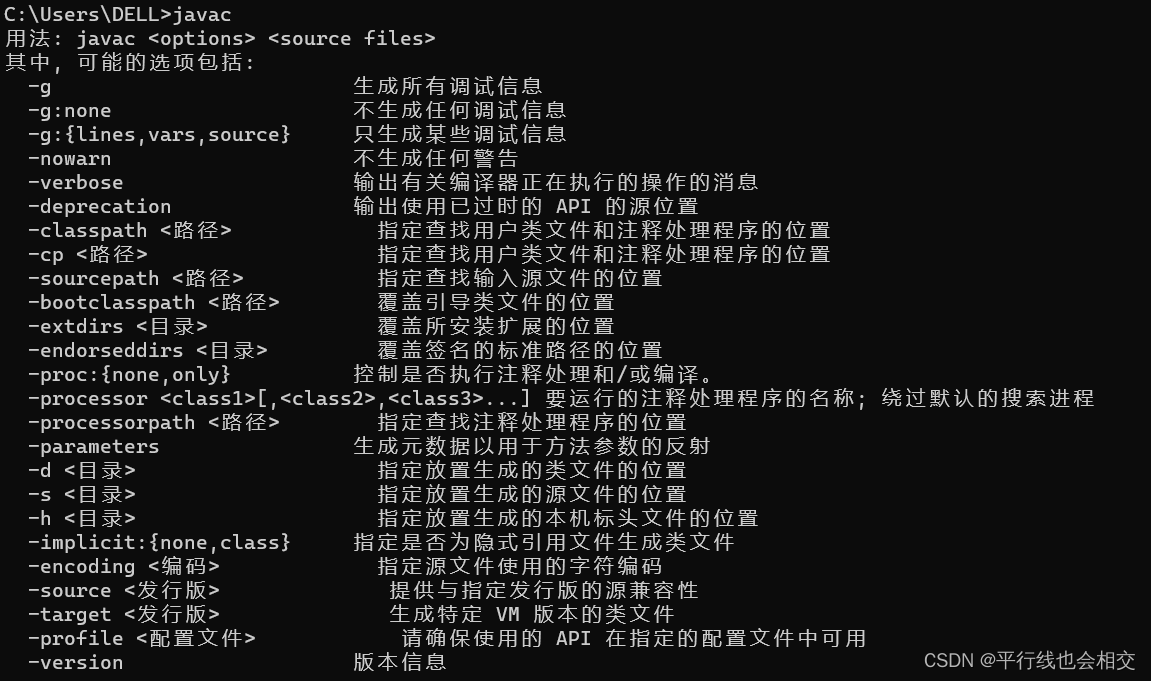
2023年最新版Windows环境下|Java8(jdk1.8)安装教程
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【JavaSE_primary】 jdk1.8的下载和使用总共分为3个步骤: jdk1.8的下载、jdk1.8的安装、配置环境变量。 目录 一、jdk1.8下载…...

linux -- jdk 的安装
jdk 的安装 jdk包下载 链接: https://pan.baidu.com/s/1wa1TJGtCPKQqeCGDZWaP6g 密码: 8el6 安装及验证 ## jdk包上传次目录 /usr/local/software cd /usr/local/software tar -zxvf /usr/local/software/jdk-8u212-linux-x64.tar.gz -C /usr/local cd /usr/local mv jdk1…...

网络安全—黑客技术(学习笔记)
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...
Java入职第十一天,深入了解静态代理和动态代理(jdk、cglib)
一、代理模式 一个类代表另一个类去完成扩展功能,在主体类的基础上,新增一个代理类,扩展主体类功能,不影响主体,完成额外功能。比如买车票,可以去代理点买,不用去火车站,主要包括静态代理和动态代理两种模式。 代理类中包含了主体类 二、静态代理 无法根据业务扩展,…...

Snappy算法:高速压缩和解压缩技术的顶尖玩家
文章首发地址 Snappy是一种快速压缩和解压缩数据的算法。它是由Google开发的,旨在提供高速的压缩和解压缩速度,同时保持较高的压缩比。 Snappy算法的设计目标是追求速度而不是最高的压缩率。相比于其他压缩算法(如Gzip或LZ77)&am…...
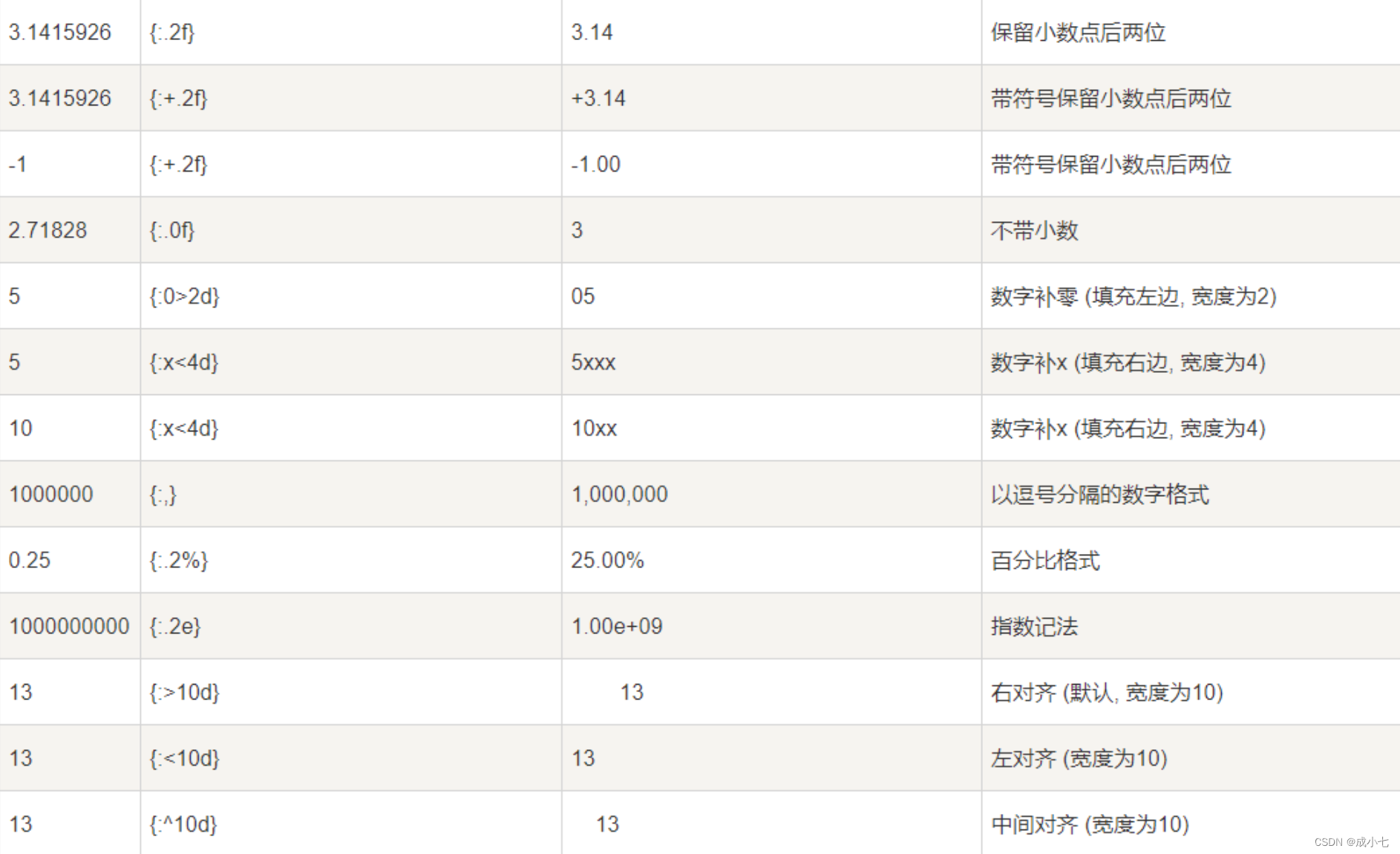
Python中的format()函数详细讲解
注:所以代码皆成功运行,可直接复制运行 一、基本使用 1、Python中的format()函数是一个格式字符串的函数,通过花括号{}识别替换字段,从而完成字符串的格式化。 #format后面放数字、字符串都可以 print("{}喜欢{}岁的{}&qu…...
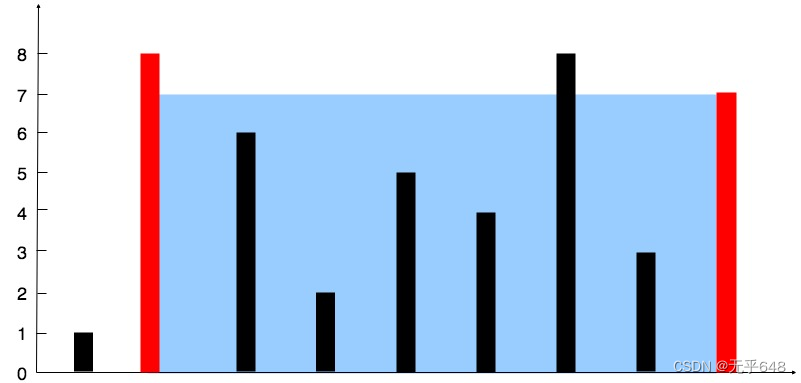
11. 盛最多水的容器(c++题解)
11. 盛最多水的容器(c题解) 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大…...

历史最佳二季度表现后,爱奇艺想为用户提供更多价值
以爱奇艺为首,随着长视频平台相继转变运营思路,走向盈利目标,最早完成蜕变的爱奇艺,已开始迈向下一阶段。 近日,爱奇艺发布了截至6月30日的2023年第二季度财报。除了依然亮眼的内容表现、业绩成果外,爱奇艺…...
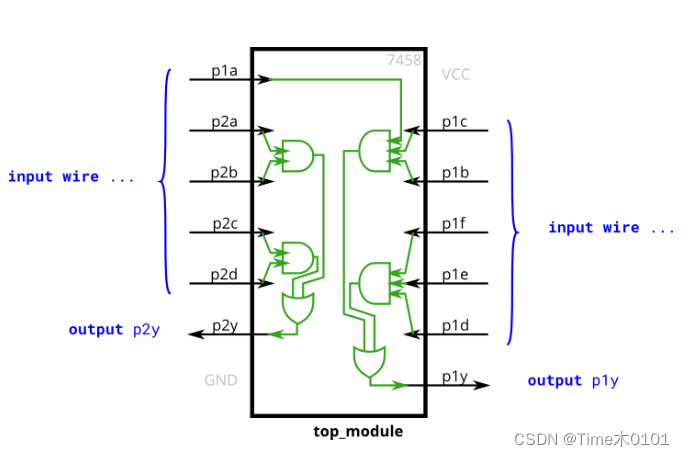
HDLBits-Verilog学习记录 | Verilog Language-Basics(2)
文章目录 9.Declaring wires | wire decl10. 7458 chip 9.Declaring wires | wire decl problem:Implement the following circuit. Create two intermediate wires (named anything you want) to connect the AND and OR gates together. Note that the wire that feeds the …...

Ubuntu22.0网络/网卡丢失
Ubuntu22.0开机突然连不上网了,右上角网络图标消失了,设置里网络也没有了“有线”,只剩下VPN了,试了好多种办法,最终终于解决了。 看到有些直接用的下面的两条命令,有解决的,不过我这不行。 s…...

Linux 常用
系统信息 查看CPU信息(型号) cat /proc/cpuinfo | grep name | cut -f2 -d: | uniq -c查看物理CPU个数 cat /proc/cpuinfo | grep "physical id" | sort | uniq | wc -l查看每个物理CPU中core的个数(即核数) cat /proc/cpuinfo | grep "c…...
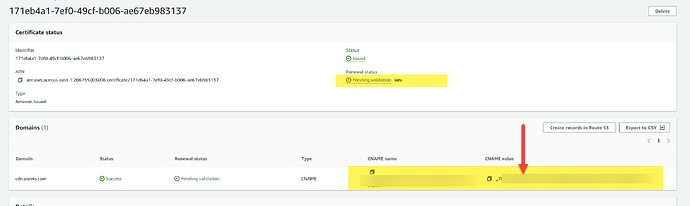
AWS 提示证书签名过期无法自动更新
如果域名没有通过验证的话,证书的过去是没有办法自动更新的。 验证的方式也非常简单,通过下面的配置,把 CNAME添加到你的域名上面,AWS 就可会自动完成验证了。 当添加完成后,AWS 验证需要的时间大致在 30 分钟到 1 个…...
 简介 基本提交相关命令)
Git版本管理(01) 简介 基本提交相关命令
1 git简介 Git是一种分布式版本控制工具,用于跟踪文件和代码的变化,协调多个开发者之间的协作,并提供版本控制和代码管理的功能。 官方学习可参考文档-> Git版本控制工具特点总结如下: 分布式版本控制:Git采用分…...

解决 vue项目报错:digital envelope routines::unsupported
出现这个错误是因为 node.js V17版本中最近发布的OpenSSL3.0, 而OpenSSL3.0对允许算法和密钥大小增加了严格的限制,可能会对生态系统造成一些影响. 方法1:运行前$ npm run serve前 先运行 export NODE_OPTIONS--openssl-legacy-provider 方法2…...
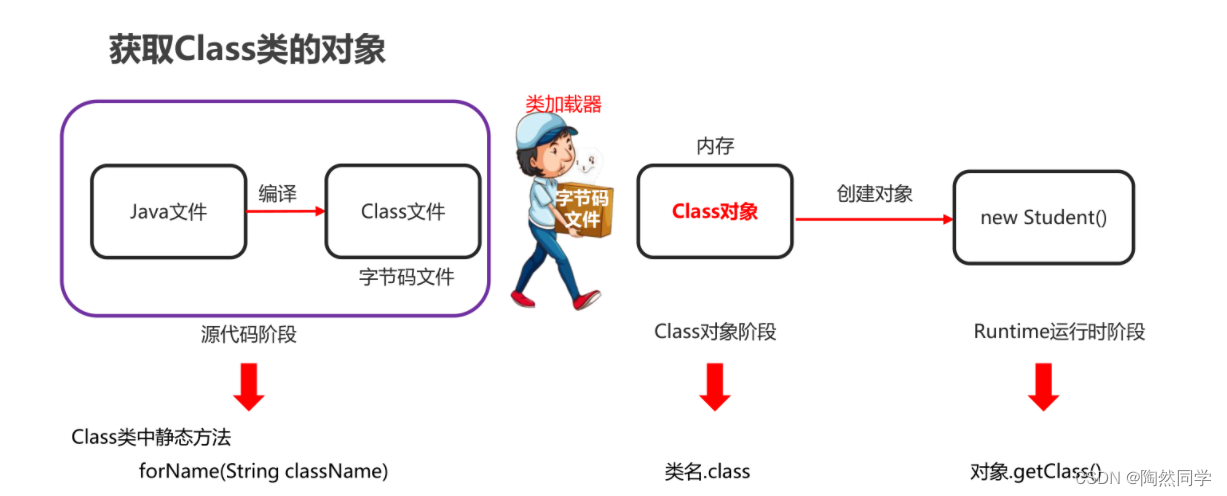
【Java基础增强】类加载器和反射
1.类加载器 1.1类加载器【理解】 作用 负责将.class文件(存储的物理文件)加载在到内存中 1.2类加载的过程【理解】 类加载时机 创建类的实例(对象) 调用类的类方法 访问类或者接口的类变量,或者为该类变量赋值 …...

【Java】数据类型变量
【Java】数据类型&变量 文章目录 【Java】数据类型&变量1、字面常量2、数据类型3、变量3.1 整型变量3.1.1 整型变量3.1.2 长短整型变量3.1.3 字节型变量 3.2 浮点型变量3.2.1 双精度浮点型3.2.2 单精度浮点型 3.3 字符型变量3.4 布尔型变量3.5 类型转换3.5.1 自动类型转…...

护目镜佩戴检测识别算法
护目镜佩戴检测识别算法通过opencvpython网络深度学习模型,护目镜佩戴检测识别算法实时监测工人的护目镜佩戴情况,发现未佩戴或错误佩戴的情况,及时提醒调整。与C / C等语言相比,Python速度较慢。也就是说,Python可以使…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
