探索经典算法问题与解决方案
探索经典算法问题与解决方案
在计算机科学领域,有许多经典算法问题需要我们思考和解决。本文将深入介绍一些著名的经典算法问题,包括旅行商问题、背包问题的变种、N皇后问题、钢条切割问题、最大子数组和问题、最长公共子串问题以及矩阵连乘问题,并提供完整的Java代码示例。
1. 旅行商问题(TSP)
旅行商问题是一种组合优化问题,要求在给定的一组城市和距离情况下,找到一条最短的路径,使得每个城市恰好被访问一次,最终回到出发城市。
public class TravelingSalesmanProblem {static int[][] graph = {{0, 29, 20, 21},{29, 0, 15, 18},{20, 15, 0, 16},{21, 18, 16, 0}};static int tsp(int mask, int pos) {if (mask == (1 << graph.length) - 1) {return graph[pos][0];}int minCost = Integer.MAX_VALUE;for (int city = 0; city < graph.length; city++) {if ((mask & (1 << city)) == 0) {int newMask = mask | (1 << city);int cost = graph[pos][city] + tsp(newMask, city);minCost = Math.min(minCost, cost);}}return minCost;}public static void main(String[] args) {System.out.println("最短路径长度:" + tsp(1, 0));}
}
2. 背包问题的变种
背包问题是指在给定容量的背包和一组物品的情况下,选择不同的物品放入背包中以达到最大价值。这里我们考虑两种背包问题的变种:多重背包问题和无限背包问题。
2.1 多重背包问题
public class MultipleKnapsackProblem {static int knapsack(int[] values, int[] weights, int[] quantities, int capacity) {int n = values.length;int[][] dp = new int[n + 1][capacity + 1];for (int i = 1; i <= n; i++) {for (int w = 1; w <= capacity; w++) {dp[i][w] = dp[i - 1][w];for (int k = 1; k <= quantities[i - 1] && k * weights[i - 1] <= w; k++) {dp[i][w] = Math.max(dp[i][w], dp[i - 1][w - k * weights[i - 1]] + k * values[i - 1]);}}}return dp[n][capacity];}public static void main(String[] args) {int[] values = {10, 30, 20};int[] weights = {5, 10, 15};int[] quantities = {2, 2, 1};int capacity = 50;System.out.println("最大价值:" + knapsack(values, weights, quantities, capacity));}
}
2.2 无限背包问题
public class UnboundedKnapsackProblem {static int knapsack(int[] values, int[] weights, int capacity) {int n = values.length;int[] dp = new int[capacity + 1];for (int w = 1; w <= capacity; w++) {for (int i = 0; i < n; i++) {if (weights[i] <= w) {dp[w] = Math.max(dp[w], dp[w - weights[i]] + values[i]);}}}return dp[capacity];}public static void main(String[] args) {int[] values = {10, 30, 20};int[] weights = {5, 10, 15};int capacity = 50;System.out.println("最大价值:" + knapsack(values, weights, capacity));}
}
3. N皇后问题
N皇后问题是指在N×N的棋盘上放置N个皇后,使得任意两个皇后都不能互相攻击。攻击包括在同一行、同一列或同一对角线上。
public class NQueensProblem {static int n = 8;static boolean isSafe(int[][] board, int row, int col) {for (int i = 0; i < col; i++) {if (board[row][i] == 1) {return false;}}for (int i = row, j = col; i >= 0 && j >= 0; i--, j--) {if (board[i][j] == 1) {return false;}}for (int i = row, j = col; i < n && j >= 0; i++, j--) {if (board[i][j] == 1) {return false;}}return true;}static boolean solveNQueensUtil(int[][] board, int col) {if (col >= n) {return true;}for (int i = 0; i < n; i++) {if (isSafe(board, i, col)) {board[i][col] = 1;if (solveNQueensUtil(board, col + 1)) {return true;}board[i][col] = 0;}}return false;}static void printSolution(int[][] board) {for (int i = 0; i < n; i++) {for (int j =0; j < n; j++) {System.out.print(board[i][j] + " ");}System.out.println();}}public static void main(String[] args) {int[][] board = new int[n][n];if (!solveNQueensUtil(board, 0)) {System.out.println("解不存在");} else {printSolution(board);}}
}
4. 钢条切割问题
钢条切割问题是指给定一根长度为n的钢条和一个价格表,求解将钢条切割成若干段使得总收益最大。
public class RodCuttingProblem {static int cutRod(int[] prices, int n) {int[] dp = new int[n + 1];dp[0] = 0;for (int i = 1; i <= n; i++) {int maxPrice = Integer.MIN_VALUE;for (int j = 1; j <= i; j++) {maxPrice = Math.max(maxPrice, prices[j - 1] + dp[i - j]);}dp[i] = maxPrice;}return dp[n];}public static void main(String[] args) {int[] prices = {1, 5, 8, 9, 10, 17, 17, 20};int n = 8;System.out.println("最大收益:" + cutRod(prices, n));}
}
5. 最大子数组和问题
最大子数组和问题是指在给定整数数组中,找到一个连续的子数组,使得该子数组的和最大。
public class MaximumSubarrayProblem {static int maxSubArray(int[] nums) {int maxSum = nums[0];int currentSum = nums[0];for (int i = 1; i < nums.length; i++) {currentSum = Math.max(nums[i], currentSum + nums[i]);maxSum = Math.max(maxSum, currentSum);}return maxSum;}public static void main(String[] args) {int[] nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};System.out.println("最大子数组和:" + maxSubArray(nums));}
}
6. 最长公共子串问题
最长公共子串问题是指在两个字符串中找到最长的连续子串,使得两个字符串都包含该子串。
public class LongestCommonSubstringProblem {static int longestCommonSubstring(String text1, String text2) {int m = text1.length();int n = text2.length();int[][] dp = new int[m + 1][n + 1];int maxLength = 0;for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {if (text1.charAt(i - 1) == text2.charAt(j - 1)) {dp[i][j] = dp[i - 1][j - 1] + 1;maxLength = Math.max(maxLength, dp[i][j]);}}}return maxLength;}public static void main(String[] args) {String text1 = "ABABC";String text2 = "BABCBA";System.out.println("最长公共子串长度:" + longestCommonSubstring(text1, text2));}
}
7. 矩阵连乘问题
矩阵连乘问题是指在给定一系列矩阵的情况下,找到一种矩阵乘法的顺序,使得计算总的乘法次数最少。
public class MatrixChainMultiplication {static int matrixChainOrder(int[] dimensions) {int n = dimensions.length;int[][] dp = new int[n][n];for (int len = 2; len < n; len++) {for (int i = 1; i < n - len + 1; i++) {int j = i + len - 1;dp[i][j] = Integer.MAX_VALUE;for (int k = i; k <= j - 1; k++) {int cost = dp[i][k] + dp[k + 1][j] + dimensions[i - 1] * dimensions[k] * dimensions[j];dp[i][j] = Math.min(dp[i][j], cost);}}}return dp[1][n - 1];}public static void main(String[] args) {int[] dimensions = {10, 30, 5, 60};System.out.println("最少乘法次数:" + matrixChainOrder(dimensions));}
}
总结
经典算法问题是计算机科学领域中的重要部分,通过深入研究和理解这些问题的解决方案,我们可以更好地理解算法设计的原则和思想。本文详细介绍了旅行商问题、背包问题的变种、N皇后问题、钢条切割问题、最大子数组和问题、最长公共子串问题以及矩阵连乘问题,每个问题都配有完整的Java代码示例,希望能够帮助您更好地掌握这些经典算法问题的解决方法。
相关文章:

探索经典算法问题与解决方案
探索经典算法问题与解决方案 在计算机科学领域,有许多经典算法问题需要我们思考和解决。本文将深入介绍一些著名的经典算法问题,包括旅行商问题、背包问题的变种、N皇后问题、钢条切割问题、最大子数组和问题、最长公共子串问题以及矩阵连乘问题&#x…...
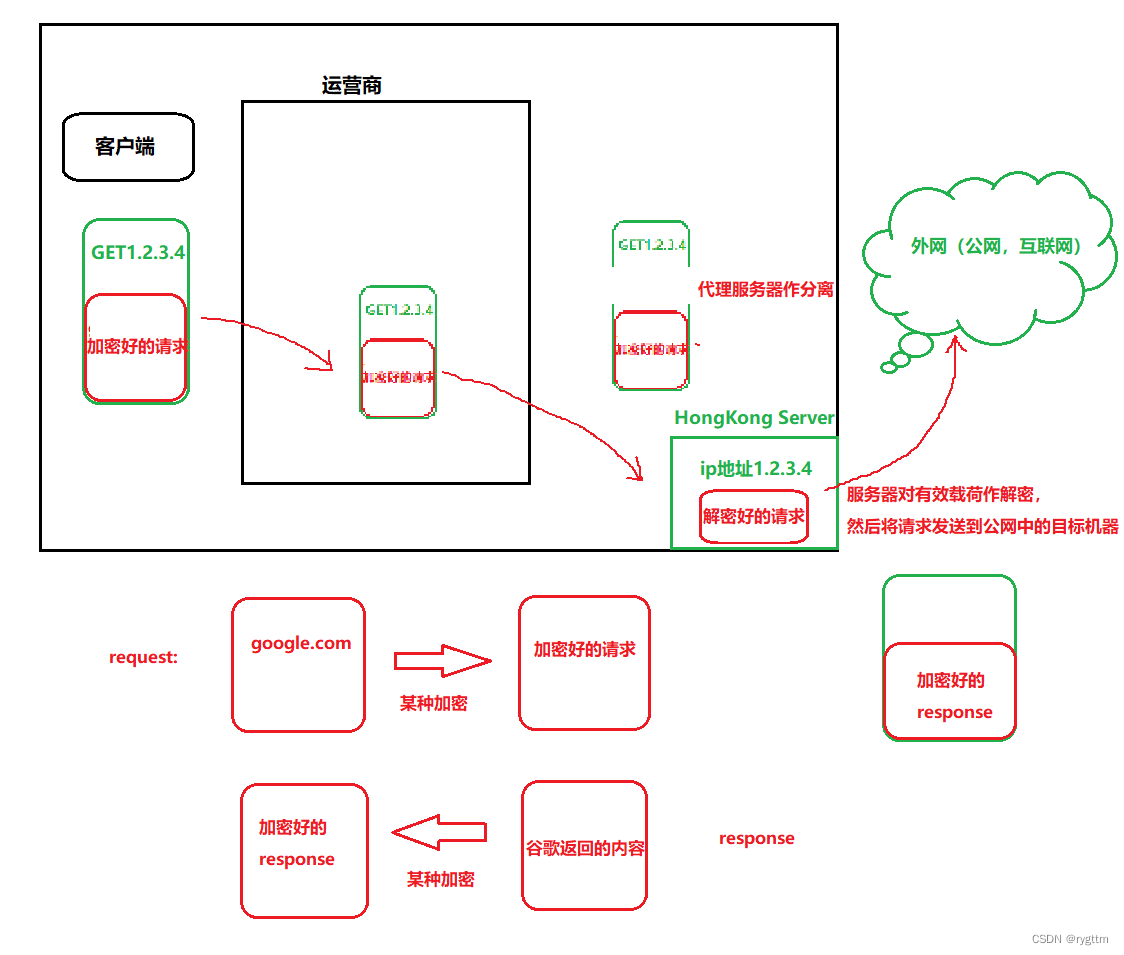
【Linux】DNS系统,ICMP协议,NAPT技术
遏制自己内心的知识优越感,才能让你发自内心的去尊重他人,避免狂妄自大,才能让你不断的丰富自己的内心。 文章目录 一、DNS系统1.DNS服务器返回域名对应的ip2.使用dig工具分析DNS过程3.浏览器中输入url后发生的事情? 二、ICMP协议…...

BI技巧丨Window应用之同环比
白茶曾介绍过OFFSET可以用来解决同环比的问题,其实微软最近推出的开窗函数WINDOW也可以用来解决同环比。 WINDOW函数基础语法 WINDOW ( from[, from_type], to[, to_type][, <relation>][, <orderBy>][, <blanks>][, <partitionBy>][, &l…...
【Mac】编译Spring 源码和Idea导入
今天我们开始Spring源码的阅读之旅。阅读Spring的源码的第一步当然是编译Spring源码。首先我们要去GitHub上将spring源码给clone下来。 笔者编译环境如下: Spring版本:5.28 https://github.com/spring-projects/spring-framework/tree/v5.2.8.RELEASE …...

手把手教你用 ANSYS workbench
ANSYS Workbench ANSYS Workbench是一款基于有限元分析(FEA)的工程仿真软件。其基本概念包括: 工作区(Workspace):工程仿真模块都在此区域内,包括几何建模、网格划分、边界条件设置、分析求解等…...
Kotlin开发笔记:协程基础
Kotlin开发笔记:协程基础 导语 本章内容与书的第十五章相关,主要介绍与协程相关的知识。总的来说,本文将会介绍Kotlin中关于异步编程的内容,主要就是与协程有关。在Kotlin中协程是利用continuations数据结构构建的,用…...
)
自学设计模式(简单工厂模式、工厂模式、抽象工厂模式)
使用工厂模式来生产某类对象(代码简化且容易维护,类之间有血缘关系,可以通过工厂类进行生产); 简单工厂模式(用于创建简单对象) 对于简单工厂模式,需要的工厂类只有一个࿱…...

NFS:使⽤ NFS 为远程客户端提供共享文件系统
写在前面 分享一些 nfs 搭建的笔记考试顺便整理内容涉及 nfs 服务端客户端的搭建配置理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的&…...
)
2022-kaggle-nlp赛事:Feedback Prize - English Language Learning(超多注释讲解)
2022-kaggle-nlp赛事:Feedback Prize - English Language Learning 零、比赛介绍 比赛地址Feedback Prize - English Language Learning | Kaggle 0.1 比赛目标 写作是一项基本技能。可惜很少学生能够磨练,因为学校很少布置写作任务。学习英语作为第…...

第十三课 宾语从句
文章目录 前言一、宾语从句1、主语及物动词宾语从句2、主语双宾动词间接宾语直接宾语3、主语特定及物动词宾语从句(作宾语)宾补4、主语be某些形容词宾语从句5、动词不定式后面的宾语从句6、动名词后面的宾语从句7、介词后面的宾语从句9、间接引语 前言 一…...
Docker容器与虚拟化技术:GitHub账户注册
目录 一、实验 1.GitHub 一、实验 1.GitHub (1)GitHub是一个面向开源及私有软件项目的托管平台,因为只支持Git作为唯一的版本库格式进行托管,故名GitHub。 (2)官网 GitHub: Let’s build from here …...
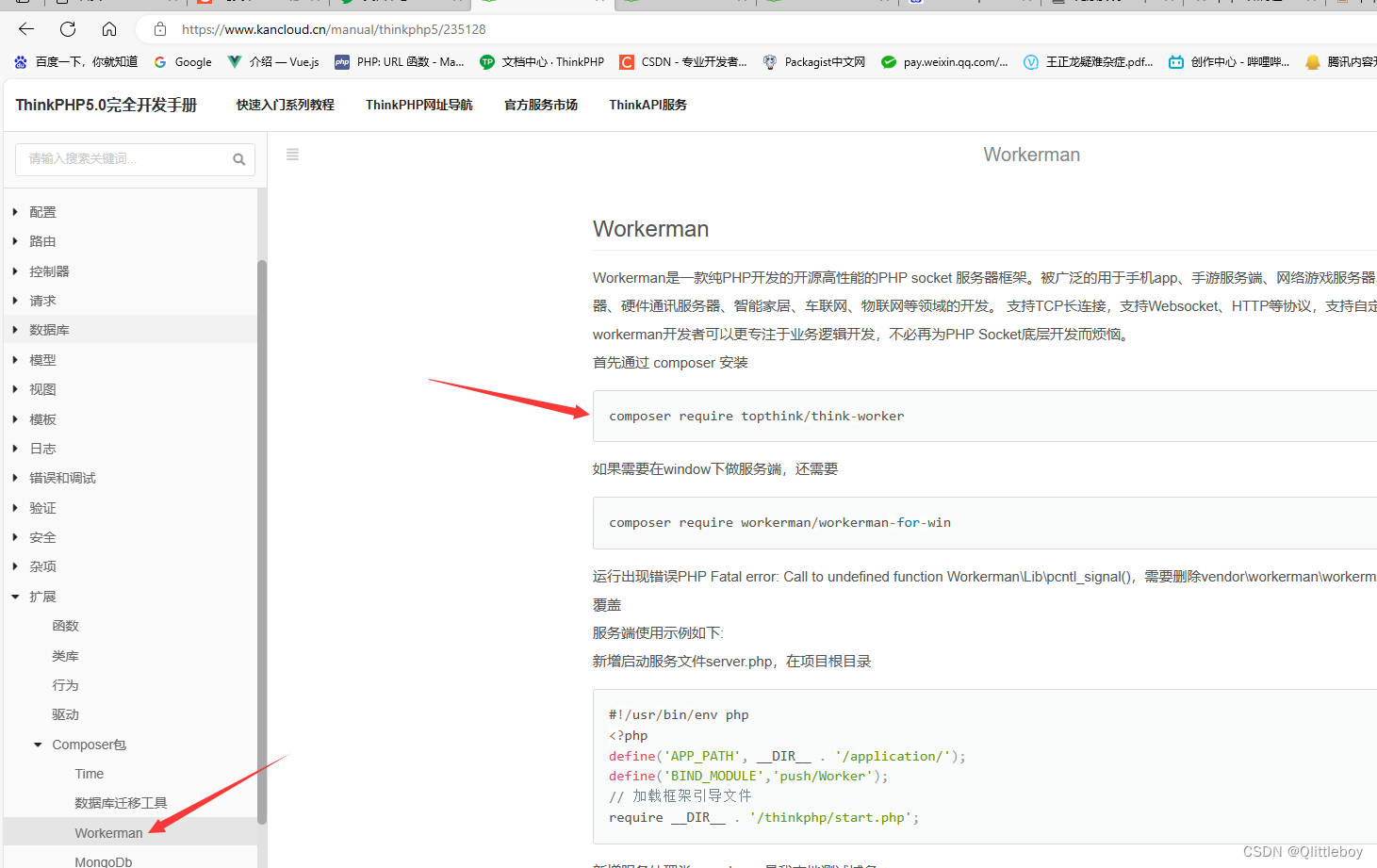
thinkphp安装workman
需要加版本,版本太高了不行 composer require topthink/think-worker1.0.*...
 测试点全过)
L1-036 A乘以B(Python实现) 测试点全过
题目 看我没骗你吧 —— 这是一道你可以在 10 秒内完成的题:给定两个绝对值不超过 100 的整数 A 和 B,输出 A 乘以 B 的值。 输入格式 输入在第一行给出两个整数 A 和 B ( − 100 ≤ A , B ≤ 100 ) A 和 B(−100≤…...

代码随想录第五十三天
代码随想录第五十三天 Leetcode 1143. 最长公共子序列Leetcode 1035. 不相交的线Leetcode 53. 最大子数组和 Leetcode 1143. 最长公共子序列 题目链接: 最长公共子序列 自己的思路:没想出来!!! 正确思路:首先这道题由于是涉及到了两个数组&…...

cmd - 如何在不重启的情况下让修改后的hosts生效
cmd - 如何在不重启的情况下让修改后的hosts生效 亲测有效 一般在修改了hosts文件后,需要重启电脑才能生效;其实可以不通过重启电脑也可以令其生效,方法如下: 打开cmd窗口输入ipconfig /flushdns,然后回车。…...

echarts实现双x轴并且分组滚动效果
var myChart echarts.init(document.getElementById(allOutPut1));var option {legend: {itemHeight: 10, // 图例icon高度itemWidth: 16, // 图例icon宽度icon:rect,//设置为矩形top:2%,right:10%,},tooltip: {trigger: axis,axisPointer: {type: shadow},textStyle: {fontS…...
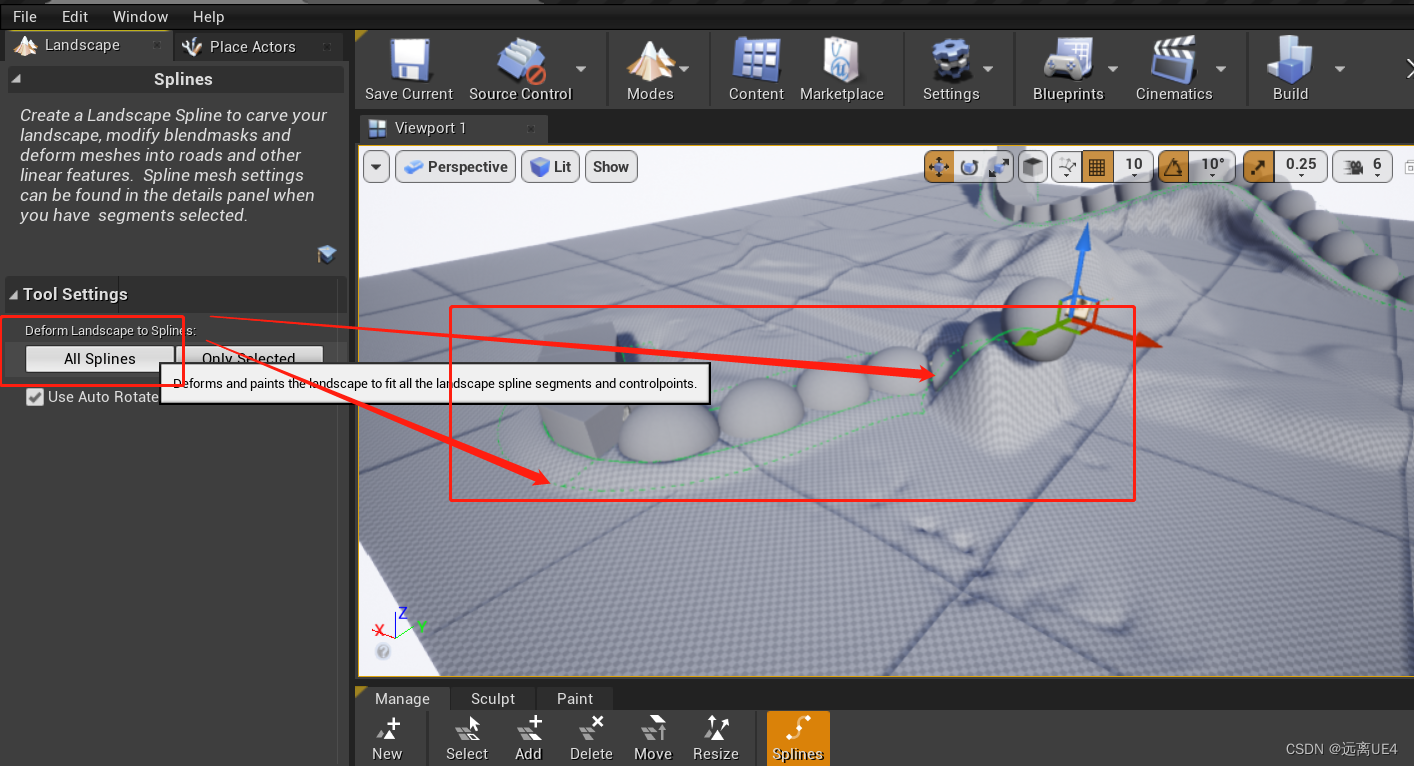
UE4 地形编辑基础知识 学习笔记
之前自己写过这样的功能,今天看到一个UE现成的 点击地形,选择样条 按住CTRL键点击屏幕中某一个点会在场景内生成一个这样的图标 再点两次,会生成B样条的绿线条 点击号再选择一个模型,会生成对应的链条状的mesh 拉高最远处的一个图…...

AcWing算法提高课-5.5.2最大公约数
宣传一下 算法提高课整理 CSDN个人主页:更好的阅读体验 原题链接 题目描述 给定整数 N N N,求 1 ≤ x , y ≤ N 1 \le x,y \le N 1≤x,y≤N 且 gcd ( x , y ) \gcd(x,y) gcd(x,y) 为素数的数对 ( x , y ) (x,y) (x,y) 有多少对。 输入格式 输…...

Kubernetes-CKA考题详解
Kubernetes-CKA考题详解 考前须知:考试环境说明第一题:RBAC(4%)第二题:指定node设置为不可用(4%)第三题:升级kubernetes节点(7%)第四题:etcd备份还原(7%)第五题:创建NetworkPolicy(7%)第六题:创建svc(7%)第七题:创建ingress资源(7%)第八题:扩展deployme…...
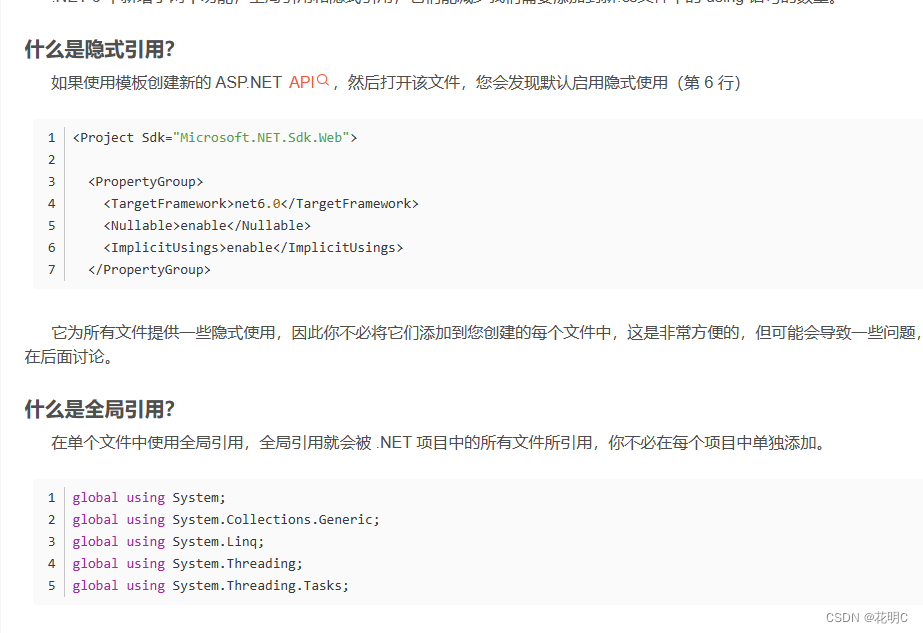
不同版本.net引用同一个项目
项目文件.csproj文件内容如下: 重点是:不能有其他的 netstandard2;net40;net45;net46;net6 <Project Sdk"Microsoft.NET.Sdk"><PropertyGroup><TargetFrameworks>netstandard2;net40;net45;net46;net6</TargetFrame…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...
