AcWing算法提高课-5.5.2最大公约数
宣传一下 算法提高课整理
CSDN个人主页:更好的阅读体验

原题链接
题目描述
给定整数 N N N,求 1 ≤ x , y ≤ N 1 \le x,y \le N 1≤x,y≤N 且 gcd ( x , y ) \gcd(x,y) gcd(x,y) 为素数的数对 ( x , y ) (x,y) (x,y) 有多少对。
输入格式
输入一个整数 N N N。
输出格式
输出一个整数,表示满足条件的数对数量。
数据范围
1 ≤ N ≤ 1 0 7 1 \le N \le 10^7 1≤N≤107
输入样例:
4
输出样例:
4
思路
首先考虑暴力。
本题答案为:
∑ i = 1 n ∑ j = 1 n ∑ p ∈ P [ gcd ( i , j ) = p ] \sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{p \in \mathbb{P}}^{}[\gcd(i,j)=p] i=1∑nj=1∑np∈P∑[gcd(i,j)=p]
把 gcd ( i , j ) = p \gcd(i,j)=p gcd(i,j)=p 变成 gcd ( i , j ) = 1 \gcd(i,j)=1 gcd(i,j)=1 然后把 p p p 除到前面的 n n n 里。
即: ∑ p ∈ P ∑ i = 1 ⌊ n p ⌋ ∑ j = 1 ⌊ n p ⌋ [ gcd ( i , j ) = 1 ] \sum_{p \in \mathbb{P}}^{}\sum_{i=1}^{\lfloor\frac{n}{p}\rfloor}\sum_{j=1}^{\lfloor\frac{n}{p}\rfloor}[\gcd(i,j)=1] p∈P∑i=1∑⌊pn⌋j=1∑⌊pn⌋[gcd(i,j)=1]
和 5.5.1 可见的点 相同,我们可以将以上代数式变换为:
2 × ∑ p ∈ P ∑ i = 1 ⌊ n p ⌋ φ ( i ) + 1 2 \times\sum_{p \in \mathbb{P}}^{}\sum_{i=1}^{\lfloor\frac{n}{p}\rfloor}\varphi(i)+1 2×p∈P∑i=1∑⌊pn⌋φ(i)+1
这里不再进行推导,读者可以自行点击上方链接进行阅读。
此时进行计算,时间复杂度近似为 O ( n 2 ln n ) \large{O(\frac{n^2}{\ln n})} O(lnnn2),将 n = 1 0 7 n=10^7 n=107 代入计算,发现超过 1 0 8 10^8 108,在 1 s 1s 1s 的时限内会 TLE \text{TLE} TLE。
我们看到 ∑ i = 1 n p φ ( n p ) \large\sum_{i=1}^{\frac{n}{p}}\varphi(\frac{n}{p}) ∑i=1pnφ(pn) 可以考虑预处理欧拉函数前缀和。
假设 s k = ∑ i = 1 k φ ( i ) \large{s_k=\sum_{i=1}^{k}\varphi(i)} sk=∑i=1kφ(i),则原式可化为:
2 × ∑ p ∈ P s ⌊ n p ⌋ + 1 \large{2 \times\sum_{p \in \mathbb{P}}^{}s_{\lfloor\frac{n}{p}\rfloor}+1} 2×p∈P∑s⌊pn⌋+1
此时我们枚举 n n n 的所有质因数进行计算就不会超时。
算法时间复杂度
预处理 φ ( i ) \varphi(i) φ(i): O ( n ) O(n) O(n);
预处理 s i s_i si: O ( n ) O(n) O(n);
计算结果: O ( n ln n ) \large{O(\frac{n}{\ln n})} O(lnnn)。
因此最高时间复杂度: O ( n ) O(n) O(n),可以过。
注意: 数论题目中,开 long long 已经是常识,所以很有必要写一条 #define int long long 避免犯错。
AC Code
C + + \text{C}++ C++
#include <iostream>
#define int long longusing namespace std;const int N = 1e7 + 10;int n;
int primes[N], cnt;
int euler[N], s[N];
bool st[N];void get_eulers(int n)
{euler[1] = 1;for (int i = 2; i <= n; i ++ ){if (!st[i]){primes[cnt ++ ] = i;euler[i] = i - 1;}for (int j = 0; primes[j] <= n / i; j ++ ){int t = primes[j] * i;st[t] = true;if (i % primes[j] == 0){euler[t] = euler[i] * primes[j];break;}euler[t] = euler[i] * (primes[j] - 1);}}
}main()
{scanf("%lld", &n);get_eulers(n); // 线性筛质数和欧拉函数for (int i = 1; i <= n; i ++ ) // 预处理欧拉函数前缀和s[i] = s[i - 1] + euler[i];int res = 0;for (int i = 0; i < cnt; i ++ ) // 枚举 n 以内的质数res += 2 * s[n / primes[i]] - 1;printf("%lld\n", res);return 0;
}

最后,如果觉得对您有帮助的话,点个赞再走吧!
相关文章:

AcWing算法提高课-5.5.2最大公约数
宣传一下 算法提高课整理 CSDN个人主页:更好的阅读体验 原题链接 题目描述 给定整数 N N N,求 1 ≤ x , y ≤ N 1 \le x,y \le N 1≤x,y≤N 且 gcd ( x , y ) \gcd(x,y) gcd(x,y) 为素数的数对 ( x , y ) (x,y) (x,y) 有多少对。 输入格式 输…...

Kubernetes-CKA考题详解
Kubernetes-CKA考题详解 考前须知:考试环境说明第一题:RBAC(4%)第二题:指定node设置为不可用(4%)第三题:升级kubernetes节点(7%)第四题:etcd备份还原(7%)第五题:创建NetworkPolicy(7%)第六题:创建svc(7%)第七题:创建ingress资源(7%)第八题:扩展deployme…...
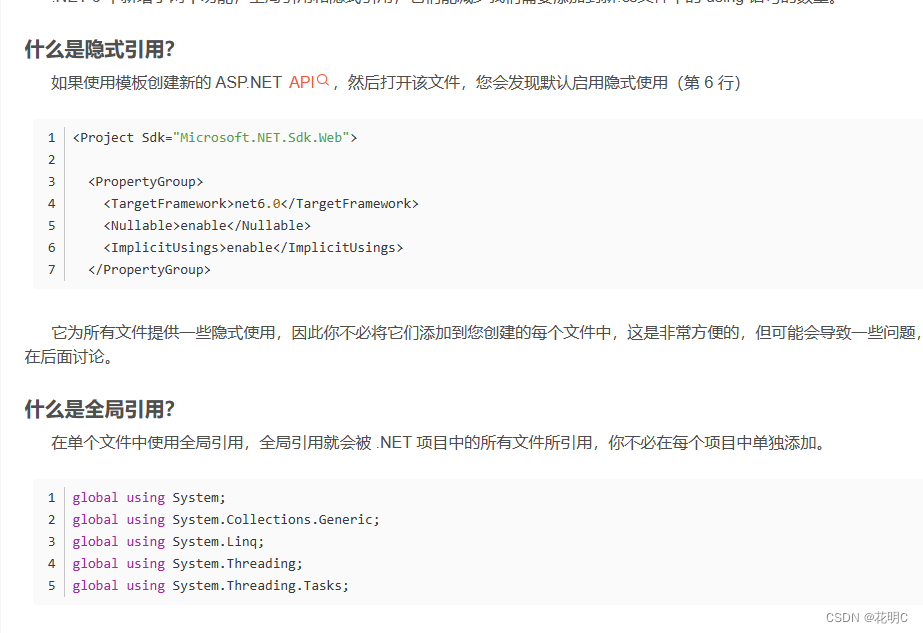
不同版本.net引用同一个项目
项目文件.csproj文件内容如下: 重点是:不能有其他的 netstandard2;net40;net45;net46;net6 <Project Sdk"Microsoft.NET.Sdk"><PropertyGroup><TargetFrameworks>netstandard2;net40;net45;net46;net6</TargetFrame…...

软件开发企业SDL安全培训案例
1.背景 随着计算机技术的发展、internet及mobile应用的普遍使用,软件安全像功能、性能、稳定性一样是计算机系统的一个非常重要部分。没有安全的软件,任何美好的功能都是徒劳的,没有安全的软件,公司的机密数据、客户隐私、系统的可靠性都得不到保障.如何有效评估、开发安全、可…...

ide-eval-resetter jar包下载、源码、使用介绍
如果你在找ide-eval-resetter插件,这里告诉你,2021.3版本开始该插件正式失效。 如果你安装的JB产品版本低于2021.3版本,你确定要找ide-eval-resetter,下面提供相关链接希望对你有帮助。 ide-eval-resetter源码: Githu…...

数据压缩算法一览
文章首发地址 Huffman编码: Huffman编码是一种基于字符频率的无损压缩算法。它将出现频率较高的字符用较短的编码表示,出现频率较低的字符用较长的编码表示,从而实现压缩。Lempel-Ziv-Welch (LZW): LZW是一种基于字典的无损压缩算…...

使用Rust开发命令行工具
生成二进制文件,将其扔到环境变量的path下即可~ 用rust打造实时天气命令行工具[1] 找到合适的API 使用该api[2] 如请求 api.openweathermap.org/data/2.5/weather?qBeijing&appidyour_key: { "coord": { "lon": 116.3972, "lat&quo…...
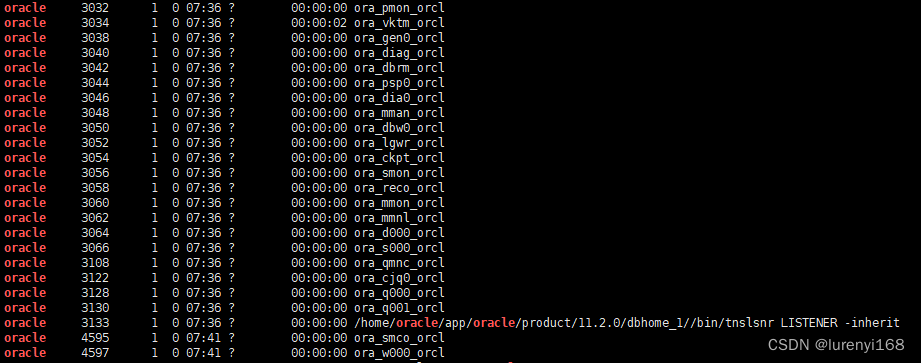
CentOS中Oracle11g进程有哪些
最近遇到Oracle数据库运行过程实例进程由于某种原因导致中止的问题,专门看了下正常Oracle数据库启动后的进程有哪些,查阅资料了解了下各进程的作用,记录如下。 oracle 3032 1 0 07:36 ? 00:00:00 ora_pmon_orcl oracle …...
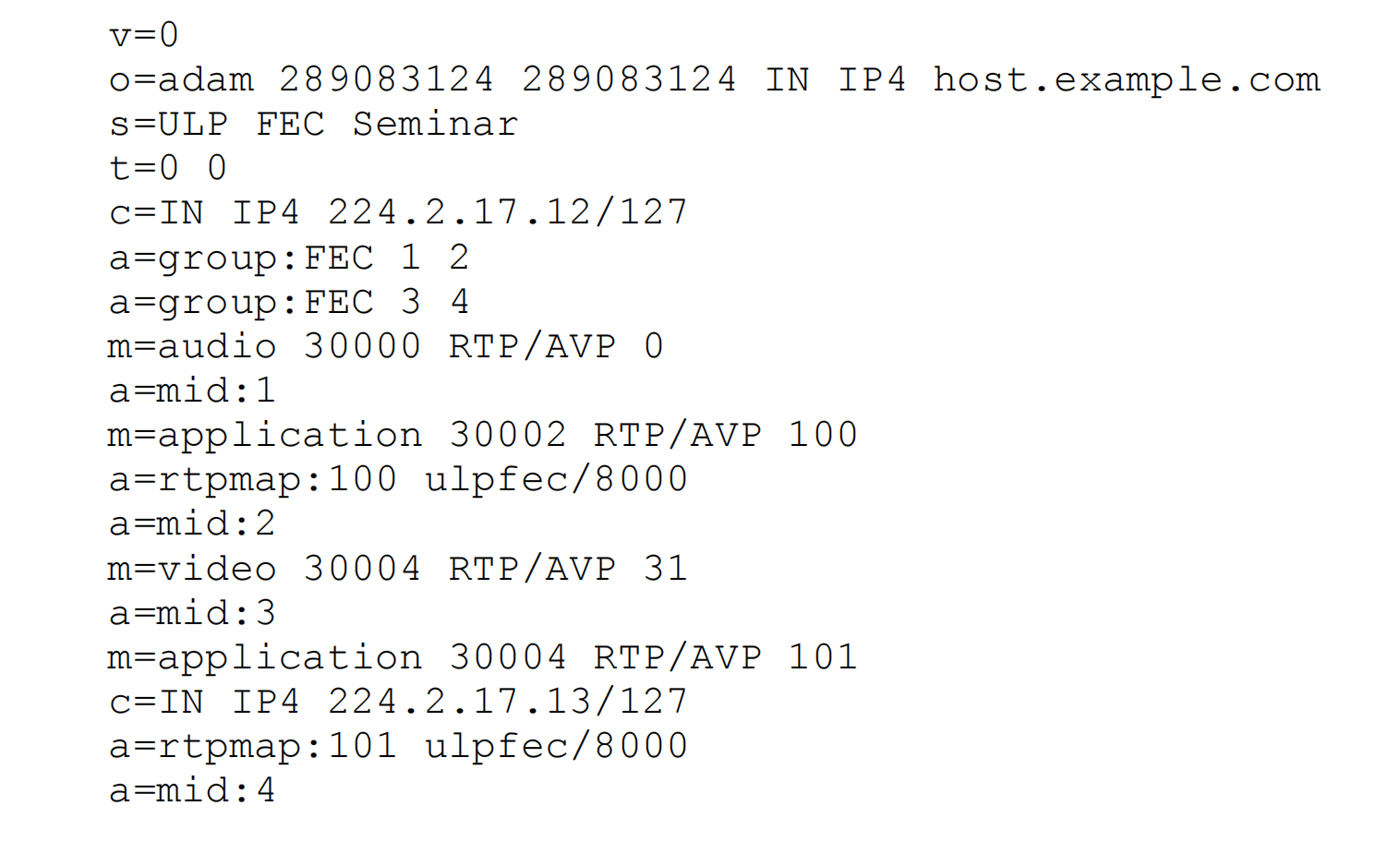
WebRTC之FEC前向纠错协议
FEC前向纠错用于丢包恢复,对媒体包进行异或或其他算法生成冗余包进行发送。如果接收端出现丢包,可以通过冗余包恢复出原始的媒体包。FEC的代价是增加码率带宽,所以一般会根据网络状况、丢包率来动态调整FEC冗余系数,也会结合NACK/…...

软件测试技术分享丨使用Postman搞定各种接口token实战
现在许多项目都使用jwt来实现用户登录和数据权限,校验过用户的用户名和密码后,会向用户响应一段经过加密的token,在这段token中可能储存了数据权限等,在后期的访问中,需要携带这段token,后台解析这段token才…...
GBU812-ASEMI逆变器专用整流桥GBU812
编辑:ll GBU812-ASEMI逆变器专用整流桥GBU812 型号:GBU812 品牌:ASEMI 芯片个数:4 封装:GBU-4 恢复时间:>50ns 工作温度:-55C~150C 浪涌电流:200A 正向电流&…...

D2007在64位Win7出现 delphi 2007 assertion failure thread32.cpp 的解决办法
Delphi2007 原来安装在Win7 下 运行正常, 自从升级到Win10 ,新建工程运行然后关闭报错, 报错信息如下: --------------------------- bds.exe - bordbk105N.dll --------------------------- Assertion failure: "(!"S…...
windows10 docker 安装在D盘
win10安装docker后发现c盘空间急速减少,360管家查看发现images镜像安装在C盘,于是重装docker desktop以为在安装过程中能够选择,遗憾的是没有提供选择权限,默认直接就安装到了c盘。 desktop 迁移 百度得知可以将c盘的docker安装…...

Scikit-learn强化学习代码批注及相关练习
一、游戏介绍 木棒每保持平衡1个时间步,就得到1分。每一场游戏的最高得分为200分每一场游戏的结束条件为木棒倾斜角度大于41.8或者已经达到200分。最终获胜条件为最近100场游戏的平均得分高于195。代码中env.step(),的返回值就分…...
执行jmeter端口不够用报错(Address not available)
执行jmeter端口不够用报错(Address not available) linux解决方案 // 增加本地端口范围 echo 1024 65000 > /proc/sys/net/ipv4/ip_local_port_range// 启用快速回收TIME_WAIT套接字 sudo sysctl -w net.ipv4.tcp_tw_recycle 1// 启用套接字的重用 sudo sysctl -w net.ipv4.…...
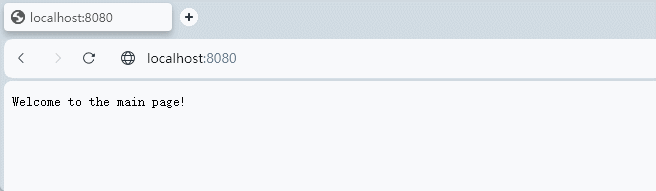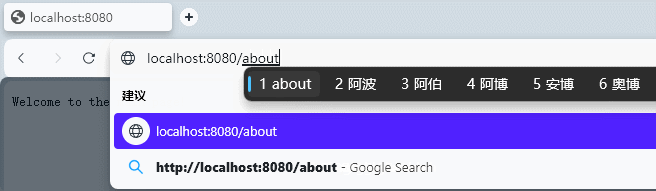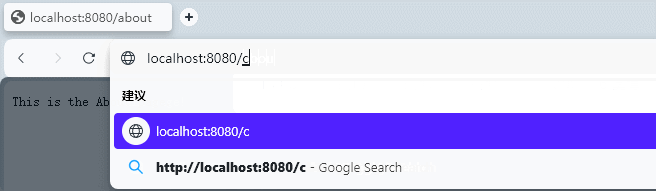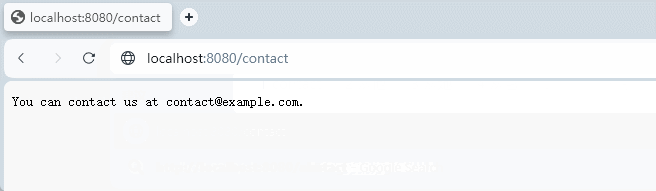
【Go Web 篇】从零开始:构建最简单的 Go 语言 Web 服务器
随着互联网的迅速发展,Web 服务器成为了连接世界的关键组件之一。而在现代编程语言中,Go 语言因其卓越的性能和并发能力而备受青睐。本篇博客将带你从零开始,一步步构建最简单的 Go 语言 Web 服务器,让你对 Go 语言的 Web 开发能力…...

Android系统-性能-优化概述
目录 引言: APP优化: 网络优化: 内存优化: 卡顿优化: 引言: 先大概对Android性能优化做一个简单分类和梳理。由于性能影响因素多,比如本文分类的APP,内存,网络&…...
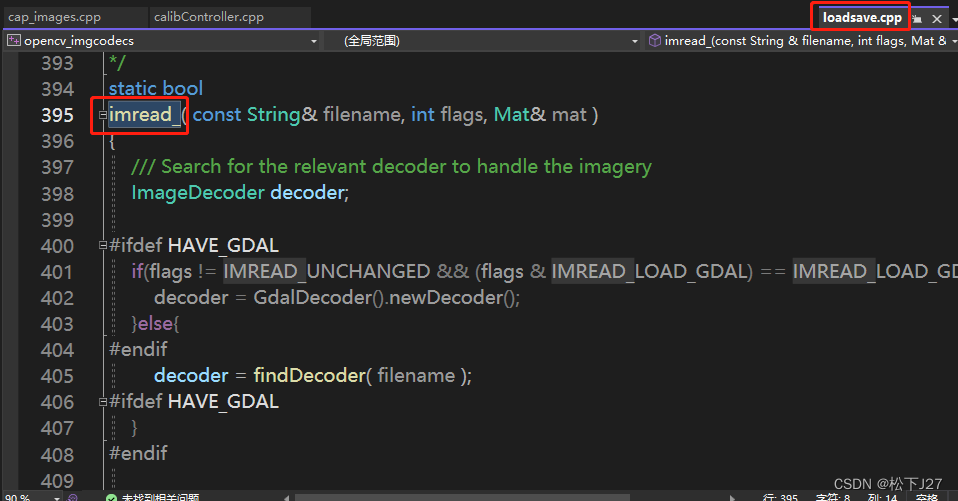
用Cmake build OpenCV后,在VS中查看OpenCV源码的方法(环境VS2022+openCV4.8.0) Part II
用Cmake build OpenCV后,在VS中查看OpenCV源码的方法 Part II 用Cmake build OpenCV后,在VS中查看OpenCV源码的方法(环境VS2022openCV4.8.0) Part I_松下J27的博客-CSDN博客 在上一篇文章中,我用cmake成功的生成了ope…...
深度学习5:长短期记忆网络 – Long short-term memory | LSTM
目录 什么是 LSTM? LSTM的核心思路 什么是 LSTM? 长短期记忆网络——通常被称为 LSTM,是一种特殊的RNN,能够学习长期依赖性。由 Hochreiter 和 Schmidhuber(1997)提出的,并且在接下来的工作中…...

LabVIEW开发灭火器机器人
LabVIEW开发灭火器机器人 如今,自主机器人在行业中有着巨大的需求。这是因为它们根据不同情况的适应性。由于消防员很难进入高风险区域,自主机器人出现了。该机器人具有自行检测火灾的能力,并通过自己的决定穿越路径。 由于消防安全是主要问…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
