数学建模-建模算法(4)
python虽然不是完全为数学建模而生的,但是它完整的库让它越来越适合建模了。
- 线性规划:使用scipy.optimize.linprog()函数
```python
from scipy.optimize import linprogc = [-1, 4]
A = [[-3, 1], [1, 2]]
b = [6, 4]
x0_bounds = (None, None)
x1_bounds = (-3, None)
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='highs')
print(res)
```
- 整数规划:使用scipy.optimize.linprog()函数,并将目标函数系数转换为整数
```python
from scipy.optimize import linprogc = [-1, 4]
A = [[-3, 1], [1, 2]]
b = [6, 4]
x0_bounds = (None, None)
x1_bounds = (-3, None)
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='highs', integer=True)
print(res)
```
- 多元规划:使用scipy.optimize.linprog()函数
```python
from scipy.optimize import linprogc = [-1, 4]
A = [[-3, 1, 1], [1, 2, 3]]
b = [6, 4, 5]
x0_bounds = (None, None, None)
x1_bounds = (-3, -3, -3)
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='highs')
print(res)
```
- 二次规划:使用scipy.optimize.linprog()函数,并将目标函数系数转换为平方项
```python
from scipy.optimize import linprogc = [-1, 4]
A = [[-3, 1], [1, 2]]
b = [6, 4]
x0_bounds = (None, None)
x1_bounds = (-3, None)
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='highs', square_root=True)
print(res)
```
- 遗传算法:使用DEAP库
```python
from deap import base, creator, tools, algorithms
import randomcreator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", list, fitness=creator.FitnessMin)toolbox = base.Toolbox()
toolbox.register("attr_bool", random.randint, 0, 1)
toolbox.register("individual", tools.initRepeat, creator.Individual, toolbox.attr_bool, n=100)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)def evalOneMax(individual):return sum(individual),toolbox.register("evaluate", evalOneMax)
toolbox.register("mate", tools.cxTwoPoint)
toolbox.register("mutate", tools.mutFlipBit, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3)population = toolbox.population(n=300)
algorithms.eaSimple(population, toolbox, cxpb=0.5, mutpb=0.2, ngen=40)
```
- 动态规划:使用scipy.optimize.linprog()函数,并将目标函数转换为动态规划问题
```python
from scipy.optimize import linprogc = [-1, 4]
A = [[-3, 1], [1, 2]]
b = [6, 4]
x0_bounds = (None, None)
x1_bounds = (-3, None)
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='highs')
print(res)
```
- 贪心算法:使用scipy.optimize.linprog()函数,并将目标函数转换为贪心策略
```python
from scipy.optimize import linprogc = [-1, 4]
A = [[-3, 1], [1, 2]]
b = [6, 4]
x0_bounds = (None, None)
x1_bounds = (-3, None)
res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='highs', options={'disp': True})
while not res.success:if not res.fun:print("Objective function value is 0 at point %s" % res.x)breakif res.status == 4:print("The algorithm could not find a feasible solution for the problem")breakprint(res)res = linprog(c, A_ub=A, b_ub=b, bounds=[x0_bounds, x1_bounds], method='highs', options={'disp': True})
print(res)
```下次再更新一些高难度的常见算法。
相关文章:
)
数学建模-建模算法(4)
python虽然不是完全为数学建模而生的,但是它完整的库让它越来越适合建模了。 - 线性规划:使用scipy.optimize.linprog()函数 python from scipy.optimize import linprogc [-1, 4] A [[-3, 1], [1, 2]] b [6, 4] x0_bounds (None, None) x1_bound…...

python之函数返回数据框
1.原始文件 ##gff-version 3 Chr1A IWGSC_v2.1 gene 40098 70338 33 - . IDTraesCS1A03G0000200;previous_idTraesCS1A02G000100;primconfHC;NameTraesCS1A03G0000200;cdsCDS_OK;mappingfullMatchWithMissmatches Chr1A IWGSC_v2.1 mRN…...

电子商务安全体系架构技术方面
技术方面是本文所要阐述的主要方面,因为它能够依靠企业自 身的努力来达到令人满意的安全保障效果。目前,关于电子商务安全体系的研究比 较多,有基于层次的体系,也有基于对象的体系,还有基于风险管理的体系࿰…...

新安装IDEA 常用插件、设置
新安装IDEA 常用插件、设置 mybatiscodeHelperProRestfulToolkit-fixJrebelmybatis log freepojo to jsonGrep ConsoleMaven HelperCamelCaseCamelCase常用设置 mybatiscodeHelperPro mapper.xml 编码校验 sql 生成,代码生成 RestfulToolkit-fix URI 跳转到对应的…...

ChromeOS 的 Linux 操作系统和 Chrome 浏览器分离
导读科技媒体 Ars Technica 报道称,谷歌正在将 ChromeOS 的浏览器从操作系统中分离出来 —— 让它变得更像 Linux。虽然目前还没有任何官方消息,但这项变化可能会在本月的版本更新中推出。 据介绍,谷歌将该项目命名为 "Lacros"——…...
哔哩哔哩 B站 bilibili 视频倍速设置 视频倍速可自定义
目录 一、复制如下代码 二、在B站视频播放页面进入控制台 三、将复制的代码粘贴到下方输入框,并 回车Enter 即可 四、然后就可以了 一、复制如下代码 (该代码用于设置倍速为3,最后的数值是多少就是多少倍速,可以带小数点&#…...
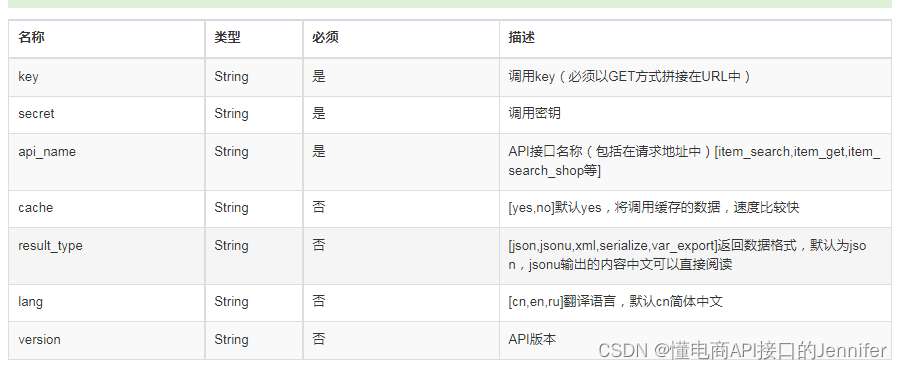
Lazada商品详情接口 获取Lazada商品详情数据 Lazada商品价格接
一、引言 随着电子商务的迅速发展和普及,电商平台之间的竞争也日趋激烈。为了提供更好的用户体验和更高效的后端管理,Lazada作为东南亚最大的电商平台之一,开发了一种商品详情接口(Product Detail API)。该接口允许第…...
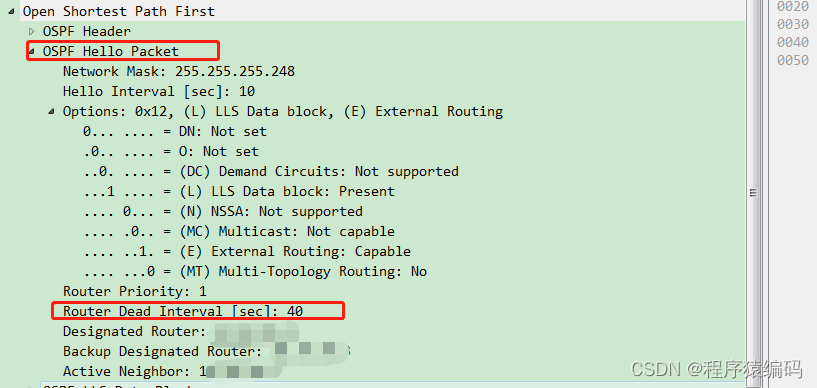
路由攻击(ospf attack)及C/C++代码实现
开放式最短路径优先(OSPF)是应用最广泛的域内路由协议之一。不幸的是,它有许多严重的安全问题。OSPF上的伪造是可能导致路由循环和黑洞的最关键的漏洞之一。 大多数已知的OSPF攻击基于伪造攻击者控制的路由器的链路状态通告(LSA&…...

nginx配置站点强制开启https
当站点域名配置完SSL证书后,如果要强制开启HTTPS,可以在站点配置文件中加上: #HTTP_TO_HTTPS_START if ($server_port !~ 443){rewrite ^(/.*)$ https://$host$1 permanent; } #HTTP_TO_HTTPS_END 附上完整的配置完SSL证书,强制…...
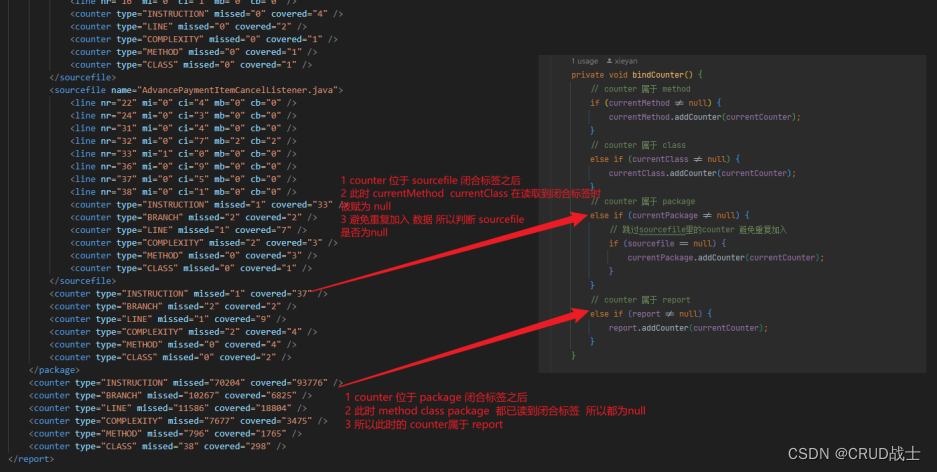
Jacoco XML 解析
1 XML解析器对比 1. DOM解析器: ○ 优点:易于使用,提供完整的文档树,可以方便地修改和遍历XML文档。 ○ 缺点:对大型文档消耗内存较多,加载整个文档可能会变慢。 ○ 适用场景:适合小型XML文档…...
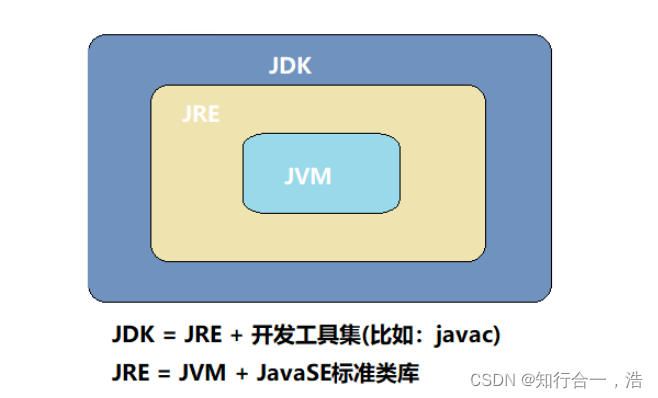
【面试题】JDK(工具包)、JRE(运行环境和基础库)、JVM(java虚拟机)之间的关系?
【面试题】JDK、JRE、JVM之间的关系? JDK(Java Development Kit):Java开发工具包,提供给Java程序员使用,包含了JRE,同时还包含了编译器javac与自带的调试工具Jconsole、jstack等。 JRE(Java Runtime Environment):Java运行时环境&…...

软件设计师学习笔记7-输入输出技术+总线+可靠性+性能指标
目录 1.输入输出技术 1.1数据传输控制方式 1.2中断处理过程 2.总线 3.可靠性 3.1可靠性指标 3.2串联系统与并联系统 3.3混合模型 4.性能指标 1.输入输出技术 即CPU控制主存与外设交互的过程 1.1数据传输控制方式 (1)程序控制(查询)方式&…...

Windows下MATLAB调用Python函数操作说明
MATLAB与Python版本的兼容 具体可参看MATLAB与Python版本的兼容 操作说明 操作说明请参看下面两个链接: 操作指南 简单说明: 我安装的是MATLAB2022a和Python3.8.6(安装时请勾选所有可以勾选的,包括路径)。对应版本安…...
【android12-linux-5.1】【ST芯片】驱动与HAL移植后数据方向异常
ST的传感器驱动与HAL一直成功后,能拿到数据了,但是设备是横屏,系统默认是竖屏。就会出现屏幕自动转动时方向是错的的情况,设备横立展示的是竖屏,设备竖立展示的是横屏。 这个是PCB上设计的传感器贴片方向和横屏不一致…...

JavaScript Es6_3笔记
JavaScript 进阶 文章目录 JavaScript 进阶编程思想面向过程面向对象 构造函数原型对象constructor 属性对象原型原型继承原型链 了解构造函数原型对象的语法特征,掌握 JavaScript 中面向对象编程的实现方式,基于面向对象编程思想实现 DOM 操作的封装。 …...

Qt产生随机数
Qt产生随机数 提问:注意:实现: 提问: 有没有小伙伴遇到这么一种情况,使用rand()和qrand()函数生成的随机数好像不是那么随机,每次都一样。那这种就叫做“伪随机”,因为没有种随机数种子&#x…...

postgresql常用函数-数学函数
postgresql常用函数 简介数学函数算术运算符绝对值取整函数乘方与开方指数与对数整数商和余数弧度与角度常量 π符号函数生成随机数 简介 函数(function)是一些预定义好的代码模块,可以将输入进行计算和处理,最终输出一个 结果值…...

【排序】快速排序(前后指针法)—— 考的最少的一种算法
以从小到大的顺序进行说明。 前后指针法 是指对于一个数组,定义前后各一个指针(prev 和 cur) prev用于卡一个比基准值大的值进行交换cur用于向前遍历出比基准值小的,和prev进行交换 图解 初始化 选出基准值4 如果cur 所在的值…...

软考:中级软件设计师:关系代数:中级软件设计师:关系代数,规范化理论函数依赖,它的价值和用途,键,范式,模式分解
软考:中级软件设计师:关系代数 提示:系列被面试官问的问题,我自己当时不会,所以下来自己复盘一下,认真学习和总结,以应对未来更多的可能性 关于互联网大厂的笔试面试,都是需要细心准备的 &…...

openCV实战-系列教程2:阈值与平滑处理(图像阈值/图像平滑处理/高斯/中值滤波)、源码解读
1、图像阈值 t图像阈值函数,就是需要判断一下像素值大于一个数应该怎么处理,小于一个数应该怎么处理 ret, dst cv2.threshold(src, thresh, maxval, type) 参数解析: src: 原始输入图,只能输入单通道图像&#…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
