2023年03月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试

第1题:最佳路径
如下所示的由正整数数字构成的三角形:
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,和最大的路径称为最佳路径。你的任务就是求出最佳路径上的数字之和。
注意:路径上的每一步只能从一个数走到下一层上和它最近的下边(正下方)的数或者右边(右下方)的数。
时间限制:1000
内存限制:65536
输入
第一行为三角形高度100>=h>=1,同时也是最底层边的数字的数目。 从第二行开始,每行为三角形相应行的数字,中间用空格分隔。
输出
最佳路径的长度数值。
样例输入
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
样例输出
30
提示
如何采用动态规划的思想,对问题进行分解。
这个问题可以使用动态规划来解决。我们可以定义一个二维数组dp,其中dp[i][j]表示从三角形顶部到第i行第j列的最佳路径的数字之和。
根据题目的要求,对于每个位置(i, j),可以从上方的位置(i-1, j-1)或者(i-1, j)到达。因此,状态转移方程可以表示为:
dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]
其中,triangle[i][j]表示三角形第i行第j列的数字。
以下是使用C语言实现的代码:
#include <stdio.h>
#include <stdlib.h>#define MAX_HEIGHT 100int max(int a, int b) {return (a > b) ? a : b;
}int calculateMaxPath(int height, int triangle[][MAX_HEIGHT]) {int dp[MAX_HEIGHT][MAX_HEIGHT];// 初始化dp数组dp[0][0] = triangle[0][0];for (int i = 1; i < height; i++) {dp[i][0] = dp[i - 1][0] + triangle[i][0];dp[i][i] = dp[i - 1][i - 1] + triangle[i][i];}// 计算最佳路径的数字之和for (int i = 2; i < height; i++) {for (int j = 1; j < i; j++) {dp[i][j] = max(dp[i - 1][j - 1], dp[i - 1][j]) + triangle[i][j];}}// 找出最大路径的数字之和int maxSum = 0;for (int j = 0; j < height; j++) {maxSum = max(maxSum, dp[height - 1][j]);}return maxSum;
}int main() {int height;scanf("%d", &height);int triangle[MAX_HEIGHT][MAX_HEIGHT];for (int i = 0; i < height; i++) {for (int j = 0; j <= i; j++) {scanf("%d", &triangle[i][j]);}}int result = calculateMaxPath(height, triangle);printf("%d\n", result);return 0;
}
在主函数中,我们首先读取输入的三角形的高度height,然后读取三角形的数字并存储在二维数组triangle中。接下来,我们调用calculateMaxPath函数计算最佳路径的数字之和,并将结果输出。
第2题:邮票收集
小A是个邮票收集爱好家,他有n种面值的邮票,每种邮票都有无数张。一天小B想要寄信,需要一共面值和为k的邮票组合。小A想要知道拼出面值为k的邮票最少需要多少张。
时间限制:1000
内存限制:131072
输入
输入是多组数据。(不超过10组) 每组数据的第一行正整数n,k,表示邮票的种类数目和目标要拼出的钱。(0 < n ≤ 100, 0 < k ≤ 1000 ) 接下来的一行有n个正整数ai(0 < ai ≤ 1000)。 若n=k=0表示输入结束。
输出
每组数据输出一行一个数,分别表示拼出k需要的最少的邮票数量。 如果不存在能够拼出k的方案,输出-1。
样例输入
4 10
1 2 3 4
5 16
1 2 3 4 5
2 7
4 5
0 0
样例输出
3
4
-1
提示
第一组数据: 10 = 4+4+2 第二组数据:16 = 5+5+5+1 第三组数据: 不存在。
这个问题可以使用动态规划来解决。我们可以定义一个一维数组dp,其中dp[i]表示拼出面值为i的邮票所需的最少数量。
根据题目的要求,对于每个金额i,我们可以考虑选择每种面值的邮票,然后更新最少数量。状态转移方程可以表示为:
dp[i] = min(dp[i], dp[i - a[j]] + 1), 其中 0 <= j < n
其中,a[j]表示第j种面值的邮票。
以下是使用C语言实现的代码:
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>#define MAX_N 100
#define MAX_K 1000int min(int a, int b) {return (a < b) ? a : b;
}int calculateMinStamps(int n, int k, int stamps[]) {int dp[MAX_K + 1];// 初始化dp数组dp[0] = 0;for (int i = 1; i <= k; i++) {dp[i] = INT_MAX;}// 计算最少邮票数量for (int i = 1; i <= k; i++) {for (int j = 0; j < n; j++) {if (i >= stamps[j] && dp[i - stamps[j]] != INT_MAX) {dp[i] = min(dp[i], dp[i - stamps[j]] + 1);}}}return (dp[k] == INT_MAX) ? -1 : dp[k];
}int main() {int n, k;while (scanf("%d %d", &n, &k) == 2) {if (n == 0 && k == 0) {break; // 输入结束}int stamps[MAX_N];for (int i = 0; i < n; i++) {scanf("%d", &stamps[i]);}int result = calculateMinStamps(n, k, stamps);printf("%d\n", result);}return 0;
}
在主函数中,我们使用一个循环来读取多组数据。对于每组数据,我们首先读取邮票的种类数目n和目标金额k,然后读取每种面值的邮票,并将它们存储在数组stamps中。接下来,我们调用calculateMinStamps函数计算拼出目标金额所需的最少邮票数量,并将结果输出。
第3题:切割回文
阿福最近对回文串产生了非常浓厚的兴趣。
如果一个字符串从左往右看和从右往左看完全相同的话,那么就认为这个串是一个回文串。例如,“abcaacba”是一个回文串,“abcaaba”则不是一个回文串。
阿福现在强迫症发作,看到什么字符串都想要把它变成回文的。阿福可以通过切割字符串,使得切割完之后得到的子串都是回文的。
现在阿福想知道他最少切割多少次就可以达到目的。例如,对于字符串“abaacca”,最少切割一次,就可以得到“aba”和“acca”这两个回文子串。
时间限制:1000
内存限制:65536
输入
输入的第一行是一个整数 T (T <= 20) ,表示一共有 T 组数据。 接下来的 T 行,每一行都包含了一个长度不超过的 1000 的字符串,且字符串只包含了小写字母。
输出
对于每组数据,输出一行。该行包含一个整数,表示阿福最少切割的次数,使得切割完得到的子串都是回文的。
样例输入
3
abaacca
abcd
abcba
样例输出
1
3
0
提示
对于第一组样例,阿福最少切割 1 次,将原串切割为“aba”和“acca”两个回文子串。 对于第二组样例,阿福最少切割 3 次,将原串切割为“a”、“b”、“c”、“d”这四个回文子串。 对于第三组样例,阿福不需要切割,原串本身就是一个回文串。
这个问题可以使用动态规划来解决。我们可以定义一个一维数组dp,其中dp[i]表示前i个字符组成的子串最少需要切割几次才能使得子串都是回文的。
根据题目的要求,对于每个位置i,我们可以考虑将子串切割为两部分,前半部分为回文子串,后半部分为回文子串。如果前半部分是回文子串,那么我们只需要判断后半部分是否是回文子串,即判断dp[j] + 1是否更小。状态转移方程可以表示为:
dp[i] = min(dp[i], dp[j] + 1), 其中 j < i 且 s[j+1...i]是回文子串
其中,s[j+1...i]表示字符串中从位置j+1到位置i的子串。
以下是使用C语言实现的代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>#define MAX_LEN 1000int min(int a, int b) {return (a < b) ? a : b;
}int isPalindrome(char str[], int start, int end) {while (start < end) {if (str[start] != str[end]) {return 0; // 不是回文串}start++;end--;}return 1; // 是回文串
}int calculateMinCut(char str[]) {int len = strlen(str);int dp[MAX_LEN];int isPal[MAX_LEN][MAX_LEN];// 初始化dp数组和isPal数组for (int i = 0; i < len; i++) {dp[i] = i; // 最多切割i次for (int j = 0; j < len; j++) {isPal[i][j] = 0;}}// 计算最少切割次数for (int i = 0; i < len; i++) {for (int j = 0; j <= i; j++) {if (str[i] == str[j] && (i - j <= 2 || isPal[j + 1][i - 1])) {isPal[j][i] = 1;if (j == 0) {dp[i] = 0; // 整个子串是回文串,不需要切割} else {dp[i] = min(dp[i], dp[j - 1] + 1);}}}}return dp[len - 1];
}int main() {int T;scanf("%d", &T);while (T--) {char str[MAX_LEN];scanf("%s", str);int result = calculateMinCut(str);printf("%d\n", result);}return 0;
}
在主函数中,我们首先读取整数T,表示有T组数据。然后,使用一个循环读取每组数据的字符串,并调用calculateMinCut函数计算最少切割次数,并将结果输出。
第4题:小球放盒子
有N个相同的球,M个不同的盒子,每个盒子最多放K个球
请计算将这N个球全部放入盒子中的方案数模1000007后的结果
时间限制:10000
内存限制:131072
输入
三个正整数,依次为N,M,K
输出
输出方案数模1000007后的结果
样例输入
4 2 3
样例输出
3
提示
总共有3种方案,依次为 { 3 , 1 },{ 2 , 2 },{ 1 , 3 }。 对于100%的数据, N,M ≤ 5000
这个问题可以使用组合数学的知识来解决。我们需要计算将N个球放入M个盒子中的方案数。
首先,考虑将N个球放入一个盒子中的方案数。由于每个盒子最多放K个球,我们可以使用0个、1个、2个…K个球来填充这个盒子。因此,对于一个盒子,可以有K+1种放球的方案。
接下来,考虑将N个球放入M个盒子中的方案数。我们可以将问题转化为将N个球放入M个盒子中,每个盒子至少放1个球的方案数。假设我们已经将每个盒子放入了一个球,那么剩余的N-M个球可以按照第一个考虑的情况放入这M个盒子中。根据乘法原理,将N-M个球放入M个盒子中的方案数为(M+1)^(N-M)。
因此,将N个球放入M个盒子中的方案数为(M+1)^(N-M)。最终的结果需要对1000007取模。
以下是使用C语言实现的代码:
#include <stdio.h>int powerMod(int base, int exponent, int mod) {int result = 1;while (exponent > 0) {if (exponent % 2 == 1) {result = (result * base) % mod;}base = (base * base) % mod;exponent /= 2;}return result;
}int calculateBallInBox(int N, int M, int K) {int result = powerMod(M + 1, N - M, 1000007);return result;
}int main() {int N, M, K;scanf("%d %d %d", &N, &M, &K);int result = calculateBallInBox(N, M, K);printf("%d\n", result);return 0;
}
在主函数中,我们首先读取整数N、M、K,分别表示球的数量、盒子的数量和每个盒子最多放置的球的数量。然后,调用calculateBallInBox函数计算将N个球放入M个盒子中的方案数,并将结果输出。
相关文章:

2023年03月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:最佳路径 如下所示的由正整数数字构成的三角形: 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,和最大的路径称为最佳路径。你的任务就是求出最佳路径上的…...

介绍一些编程语言— CSS 语言
介绍一些编程语言— CSS 语言 CSS 语言 简介 CSS,层叠样式表,是一种用来表现 HTML 或 XML 等文件样式的计算机语言。CSS 不仅可以静态地修饰网页,还可以配合各种脚本语言动态地对网页各元素进行格式化。 CSS 能够对网页中元素位置的排版进…...

一文讲清楚c/c++中的宏
一文讲清楚c/c中的宏 文章目录 一文讲清楚c/c中的宏一、如何理解这个“宏”字面的意思呢?二、c/c中的宏详解三、宏的使用场景 一、如何理解这个“宏”字面的意思呢? 在刚开始学习C语言的时候,始终有点分不清楚"宏"这个字面上的意思…...

typescript进阶语法
typescript进阶语法 interface 接口定义 interface userType {name:string,age:number,sex?:string }type接口定义 type userType {name:string,age:number,sex?:string } type userType username # 固定值写法 let user:userType age # 报错 只能等于usernamepick摘取…...

宝塔终端 查看 7003端口 占用 并且杀死
要查看端口是否被占用并杀死相关进程,你可以按照以下步骤执行: 打开宝塔面板,进入服务器管理页面。在左侧导航栏中选择「工具」,然后选择「终端」进入宝塔终端界面。输入以下命令查看端口占用情况:netstat -tuln | gr…...

可解释性的相关介绍
一、可解释性的元定义(Meta-definitions of Interpretability) The extent to which an individual can comprehend the cause of a model’s outcome. [1]The degree to which a human can consistently predict a model’s outcome. [2] 可解释性&am…...
AUTOSAR规范与ECU软件开发(实践篇)6.7 服务软件组件与应用层软件组件端口连接
在生成了BSW模块的代码后, 切换到ISOLAR-A系统级设计界面,会发现产生一些基础软件模块的服务软件组件: BswM、 ComM、 Det和EcuM等, 如图6.60所示。 图6.60 生成了BSW后的服务软件组件 此时, 如果涉及服务软件组件与应用层软件组件的交互, 就需要为应用层软件组…...
:列表)
菜鸟教程《Python 3 教程》笔记(6):列表
菜鸟教程《Python 3 教程》笔记(6) 6 列表6.1 删除列表元素6.2 列表函数和方法6.2.1 max()、min()6.2.2 reverse()6.2.3 sort() 6 列表 出处: 菜鸟教程 - Python3 列表 6.1 删除列表元素 >>> list [Google, Runoob, 1997, 2000]…...

LeetCode-56-合并区间
题目描述: 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 可以使用 LinkedList,…...

Git gui教程---番外篇 gitignore 的文件使用
想说的 .gitignore 的文件一般大型的编译器带git的都会生成,他可以将你不想提交的文件在git下忽略掉,你应该不想将一大堆编译生成的过程文件,还有一些贼大的文件提交上git的。 凡是都有例外,一些冥顽不灵的编辑器,只能…...

javaee spring 用注解的方式实现ioc
spring 用注解的方式实现ioc spring核心依赖 <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"…...
)
Linux基础(二)
这里写目录标题 一、网络管理1- 网络状态查看1.1 net-tools1.2 iproute2 2- 网络故障排除 !step1:检测当前主机和目标主机是否畅通 [ping]step2:检测网络质量,追踪路由 [traceroute]step3:检测网络质量,检查是否有数据包丢失 [mrt]step4: 检查端口是否畅通 [telnet]…...
)
155. 最小栈(中等系列)
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。 实现 MinStack 类: MinStack() 初始化堆栈对象。 void push(int val) 将元素val推入堆栈。 void pop() 删除堆栈顶部的元素。 int top() 获取堆栈顶部的元素。 int…...

用python从零开始做一个最简单的小说爬虫带GUI界面(3/3)
目录 上一章内容 前言 出现的一些问题 requests包爬取小说的不便之处 利用aiohttp包来异步爬取小说 介绍 代码 main.py test_1.py test_3.py 代码大致讲解 注意 系列总结 上一章内容 用python从零开始做一个最简单的小说爬虫带GUI界面(2/3)_…...

SpringBoot+Vue如何写一个HelloWorld
一、SpringBoot介绍 Spring Boot是一个用于创建独立且可执行的Spring应用程序的框架。它简化了基于Spring框架的应用程序的开发过程,并提供了一种快速和简便的方式来构建Java应用程序。 Spring Boot提供了自动配置机制,通过引入适当的依赖项࿰…...

深度强化学习。介绍。深度 Q 网络 (DQN) 算法
马库斯布赫霍尔茨 一. 引言 深度强化学习的起源是纯粹的强化学习,其中问题通常被框定为马尔可夫决策过程(MDP)。MDP 由一组状态 S 和操作 A 组成。状态之间的转换使用转移概率 P、奖励 R 和贴现因子 gamma 执行。概率转换P(系统动…...

【C++随笔02】左值和右值
【C随笔02】左值和右值 一、左值和右值1、字面理解——左值、右值2、字面理解的问题3、左值、右值4、左值的特征5、 右值的特征6、x和x是左值还是右值7、复合例子8、通常字面量都是一个右值,除字符串字面量以外: 二、左值引用和右值引用三、左值引用1、常…...
几个nlp的小任务(多选问答)
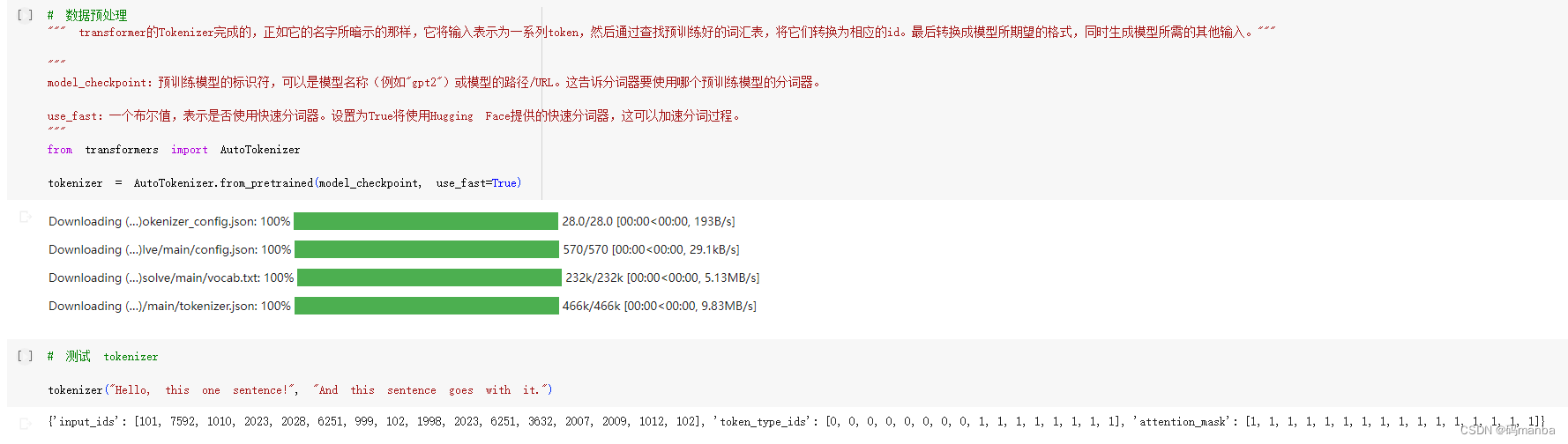
@TOC 安装库 多选问答介绍 定义参数、导入加载函数 缓存数据集 随机选择一些数据展示 进行数据预处理部分(tokenizer) 调用t...

【C++学习记录】为什么需要异常处理,以及Try Catch的使用方法
1.什么是异常,什么是错误? 程序无法保证100%正确运行,万无一失。有的错误在编译时能发现,比如:关键字拼写、变量名未定义、括号不配对、语句末尾缺分号等。这是在编译阶段发现的,称为编译错误。 有的能正常…...

孪生网络(Siamese Network)
基本概念 孪生网络(Siamese Network)是一类神经网络结构,它是由两个或更多个完全相同的网络组成的。孪生网络通常被用于解决基于相似度比较的任务,例如人脸识别、语音识别、目标跟踪等问题。 孪生网络的基本思想是将输入数据同时…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
python可视化:俄乌战争时间线关键节点与深层原因
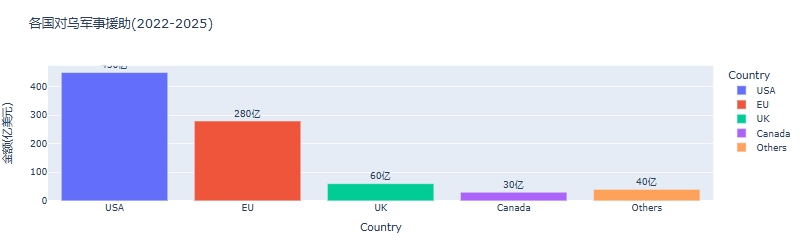
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...

【多线程初阶】单例模式 指令重排序问题
文章目录 1.单例模式1)饿汉模式2)懒汉模式①.单线程版本②.多线程版本 2.分析单例模式里的线程安全问题1)饿汉模式2)懒汉模式懒汉模式是如何出现线程安全问题的 3.解决问题进一步优化加锁导致的执行效率优化预防内存可见性问题 4.解决指令重排序问题 1.单例模式 单例模式确保某…...

Excel 怎么让透视表以正常Excel表格形式显示
目录 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总 1、创建数据透视表 2、设计 》报表布局 》以表格形式显示 3、设计 》分类汇总 》不显示分类汇总...

Kafka深度解析与原理剖析
文章目录 一、Kafka核心架构原理1. **分布式协调与选举**2. **ISR、OSR与HW机制**3. **高性能存储设计**4. **刷盘机制 (Flush)**5. **消息压缩算法**二、高可用与消息可靠性保障1. **数据高可用策略**2. **消息丢失场景与规避**3. **顺序消费保证**三、Kafka高频面试题精析1. …...

MTK-Android12-13 Camera2 设置默认视频画质功能实现
MTK-Android12-13 Camera2 设置默认视频画质功能实现 场景:部分客户使用自己的mipi相机安装到我们主板上,最大分辨率为1280720,但是视频画质默认的是640480。实际场景中,在默认视频分辨率情况下拍出来的视频比较模糊、预览也不清晰…...
