姜启源数学模型第五版第五章火箭发射升空
姜启源数学模型第五版第五章例题内容复现
- 数学建模背景
- 1.学习内容
- 火箭发射升空
- 理论知识
- 2.例题
- 3.问题分析
- 不考虑空气阻力的模型
- 考虑空气阻力的模型
- 4.代码内容复现
- 不考虑空气阻力
- 考虑空气阻力模型
数学建模背景
首先先简单的介绍数学建模是一个怎么样的内容
数学建模是一种将数学方法和技术应用于实际问题解决的过程。它通过建立数学模型来描述、分析和预测现实世界中的各种问题.
数学建模的内容可以包括以下几个方面:
1.问题定义(问题重述):明确问题的目标、约束条件和需求。
2.建立数学模型:根据问题的特点和要求,选择适当的数学方法和技术,建立描述问题的数学模型。
3.模型分析:对建立的数学模型进行分析,推导出模型的性质和特征。
4.模型求解:利用数学工具和计算机技术,求解数学模型以得出问题的解决方案。
5.模型验证和评估:验证模型的有效性和准确性,并评估解决方案的可行性和可行性。
6.结果解释和应用:解释数学模型的结果,提供对问题的洞察力,并将模型的解决方案应用于实际情况。
1.学习内容
所学习的内容的理论基础的描述
简单描述一下本文当中所要使用到的一些数学建模的理论基础的相关知识,重点在于简单了解数学建模相关知识点的应用场景,避免生搬硬套
火箭发射升空
单级小型火箭的发射
考察火箭垂直于地面发射、上升的过程:火箭垂直向上发射后,燃料以一定的速率 燃烧,火焰向后喷射,对火箭产生向前的推力,在克服地球引力和空气阻力的同时,推动 火箭加速飞行.燃料燃尽后火箭依靠获得的速度继续上升,但在引力和阻力的作用下速 度逐渐减小,直到速度等于零,火箭达到最高点.建立数学模型研究火箭上升高度、速度 和加速度的变化规律以及与火箭质量、燃料推力等因素的关系
显然,这个虚拟的场景只是实际发射火箭最初的一个阶段,若不施加其他手段,火箭将从最高点自由下落
火箭发射、上升过程所遵循的基本规律是牛顿第二定律,火箭在运动中受到燃料燃 烧的推力、地球引力和空气阻力的联合作用,其中推力与引力的作用是明确和易于处理的,空气阻力随着火箭速度的增加而变大,但二者之间的数量关系则不易确定.下面先 不考虑空气阻力,建立相对简单的模型,再通过简化、合理的假定将阻力引人模型.
理论知识
本道题当中最重要的就是动力学相关的公式以及积分直接的结合,所以大家只要知道微分方程以及牛顿第二定律
将二阶微分方程化成一阶微分方程组:
{ y 1 ′ = y 2 y 1 ( 0 ) = 1 ( 初值 ) y 2 ′ = α y 2 + β y 1 + c y 2 ( 0 ) = 1 ( 初值 ) \left\{\begin{matrix} &y^{\prime}_1=y_2 \ & y_1(0)=1(初值) \\ &y^{\prime}_2=\alpha y_2+\beta y_1+c \ & y_2(0)=1(初值) \end{matrix}\right. {y1′=y2 y2′=αy2+βy1+c y1(0)=1(初值)y2(0)=1(初值)
牛顿第二定律:
F = m a F=ma F=ma
2.例题
由于时间的关系,在每一张当中都尽可能地会挑一道两道题进行描述
问题与假设设小型火箭初始质量为 m 0 = 1600 k g m_0=1600kg m0=1600kg,其中包括 m 1 = 1080 k g m_1=1080kg m1=1080kg燃料. 火箭从地面垂直向上发射时,燃料以 r = 18 k g / s r=18kg/s r=18kg/s的速率燃烧,对火箭产生 F = 27000 N F=27000N F=27000N的恒定推力.燃料燃尽后火箭继续上升,直到达到最高点.因为火箭上升高度与地球半 径相比很小,所以可认为整个过程中受到的地球引力不变,重力加速度取 g = 9.8 m / s 2 g=9.8m/s2 g=9.8m/s2。建立火箭上升高度、速度和加速度随时间变化的数学模型,给出燃料燃尽时火箭的高 度、速度和加速度以及火箭到达最高点的时间和高度
3.问题分析
对题目进行简单的分析
不考虑空气阻力的模型
模型建立设火箭t=0时从地面x=0向上发射,火箭高度为 x ( t ) x(t) x(t),速度为 x ˙ ( t ) \dot{x}(t) x˙(t) ,加速度为 x ¨ ( t ) \ddot{x}(t) x¨(t)。火箭的质量记为 m ( t ) m(t) m(t),随燃料燃烧而减少,有 m ( t ) = m − r t m(t)=m-rt m(t)=m−rt。燃料燃尽的 m时间记为 t 1 t_1 t1,显然 t 1 = − 60 s t_1=-60s t1=−60s,t以后火箭质量保持为 m 0 − m 1 = 520 k g m_0-m_1=520kg m0−m1=520kg。火箭到达最高点的时间记为 t 2 t_2 t2, t 2 t_2 t2由 v ( t 2 ) v(t_2) v(t2)=0确定.
火箭从 x = 0 x=0 x=0处零初速地发射,上升过程中燃料燃烧阶段受到推力 F F F和重力 m ( t ) g m(t)g m(t)g的作用,按照牛顿第二定律可以写出
( m 0 − r t ) x ¨ = F − ( m 0 − r t ) g , 0 ≤ t ≤ t 1 , t 1 = m 1 r , x ( 0 ) = x ˙ ( 0 ) (m_0-rt)\ddot{x}=F-(m_0-rt)g,0≤t≤t1,t1=\frac{m_1}{r},x(0)=\dot{x}(0) (m0−rt)x¨=F−(m0−rt)g,0≤t≤t1,t1=rm1,x(0)=x˙(0)燃料燃尽后火箭只受重力作用,于是
( m 0 − m 1 ) x ¨ = − ( m 0 − m 1 ) g , t 1 < t ⩽ t 2 \left(m_{0}-m_{1}\right) \ddot{x}=-\left(m_{0}-m_{1}\right) g, \quad t_{1}<t \leqslant t_{2} (m0−m1)x¨=−(m0−m1)g,t1<t⩽t2
接下来就是分情况进行公式的推导以及计算,计算内容如下:

考虑空气阻力的模型
考虑空气阻力的模型将空气阻力与火箭的飞行速度进行了联系,得到了如下表达式
( m 0 − r t ) x ¨ = F − k x ˙ 2 − ( m 0 − r t ) g , 0 ⩽ t ⩽ t 1 , t 1 = m 1 / r , x ( 0 ) = x ˙ ( 0 ) = 0 ( m 0 − m 1 ) x ¨ = − k x ˙ 2 − ( m 0 − m 1 ) g , t 1 < t ⩽ t 2 \begin{array}{c} \left(m_{0}-r t\right) \ddot{x}=F-k \dot{x}^{2}-\left(m_{0}-r t\right) g, 0 \leqslant t \leqslant t_{1}, t_{1}=m_{1} / r, x(0)=\dot{x}(0)=0 \\ \left(m_{0}-m_{1}\right) \ddot{x}=-k \dot{x}^{2}-\left(m_{0}-m_{1}\right) g, t_{1}<t \leqslant t_{2} \end{array} (m0−rt)x¨=F−kx˙2−(m0−rt)g,0⩽t⩽t1,t1=m1/r,x(0)=x˙(0)=0(m0−m1)x¨=−kx˙2−(m0−m1)g,t1<t⩽t2
将第一个式子改写

以此为基础建立模型,绘制对应图像
4.代码内容复现
时间原因,直接进行代码的书写
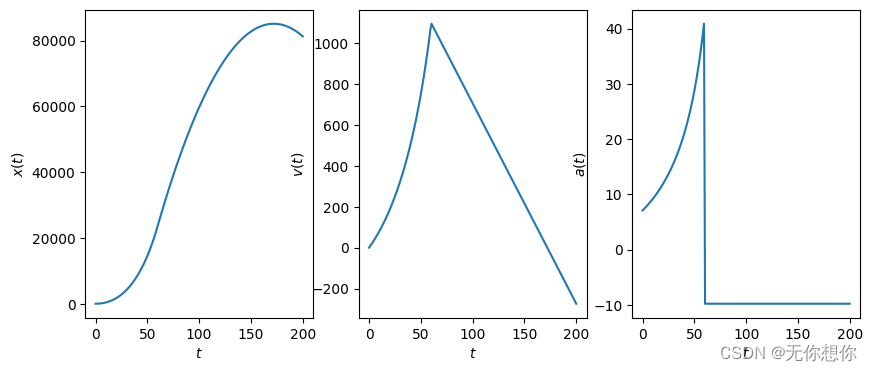
不考虑空气阻力
根据已知的内容计算可得到的具体值,在后续代码的书写当中直接代入
import numpy as np
m0=1600
F=27000
m1=1080
r=18
t1=60.0
g=9.8
v1=-g*60+(F/r)*np.log(m0/(m0-r*60))
x1=-1/2*g*60**2+F*(m0-r*60)*(np.log(m0-r*60)-1)/r**2+((F*np.log(m0))*60)/r-F*m0*(np.log(m0)-1)/r**2
print(v1)
print(x1)
1097.8951449785993
23656.36247839604
#不考虑空气阻力下的方程
from scipy.integrate import odeint
from scipy.integrate import solve_ivp
import numpy as np
import pylab as plt
import math
m0=1600
F=27000
m1=1080
r=18
t1=60.0
g=9.8
t=np.linspace(0,200,200)
v=[]
x=[]
a=[]
for i in range(0,200):if t[i]<=60:a=np.hstack([a,-g+F/(m0-r*t[i])])v=np.hstack([v,-g*t[i]+(F/r)*np.log(m0/(m0-r*t[i]))])x=np.hstack([x,-1/2*g*t[i]**2+F*(m0-r*t[i])*(np.log(m0-r*t[i])-1)/r**2+((F*np.log(m0))*t[i])/r-F*m0*(np.log(m0)-1)/r**2])else:a=np.hstack([a,-g])v=np.hstack([v,-g*(t[i]-t1)+v1])x=np.hstack([x,-1/2*g*(t[i]-t1)**2+v1*(t[i]-t1)+x1])# k=0.3
plt.figure(figsize=(10,4))
plt.subplot(131)
plt.plot(t,x[:])
plt.xlabel('$t$')
plt.ylabel('$x(t)$')plt.subplot(132)
plt.plot(t,v[:])
plt.xlabel('$t$')
plt.ylabel('$v(t)$')plt.subplot(133)
plt.plot(t,a[:])
plt.xlabel('$t$')
plt.ylabel('$a(t)$')plt.show()
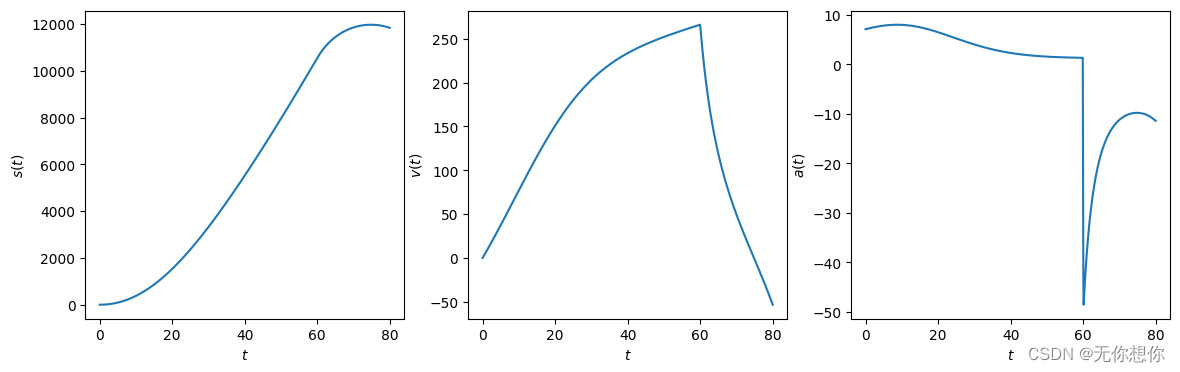
考虑空气阻力模型
使用到的是scipy.integrate当中的odeint进行计算
from scipy.integrate import odeint
from scipy.integrate import solve_ivp
import numpy as np
import pylab as plt
from sympy import symbols,diff
k=0.3
m0=1600
F=27000
m1=1080
r=18
t1=m1/r
g=9.8
def dx(x,t):x1,x2=xif t<60:return [x2,-g+(F-k*x2**2)/(m0-r*t)]elif t>=60:return [x2,-g-(k*x2**2)/(m0-m1)]# dz=lambda z,t:[z[1],-g+(F-k*z[1]**2)/(m0-r*t)]
t=np.linspace(0,80,1000)
x0=[0,0]
# solve=odeint(dz,[0,0],t)
solve=odeint(dx,x0,t)
# result=solve_ivp(dz,[0,60],[0,0],method='RK45',t_eval=None)
# plt.re('text',usetex=True)
time = np.array(t) # 时间数据
velocity = np.array(solve[:,1]) # 速度数据# 计算时间间隔
dt = time[1:] - time[:-1]# 使用中心差分法计算加速度
acceleration = np.zeros_like(velocity)
acceleration[1:-1] = (velocity[2:] - velocity[:-2]) / (2 * dt[1:])# 处理边界条件
acceleration[0] = (velocity[1] - velocity[0]) / dt[0]
acceleration[-1] = (velocity[-1] - velocity[-2]) / dt[-1]#print(acceleration)
#print(np.size(acceleration))
plt.figure(figsize=(14,4))
plt.subplot(131)
plt.plot(t,solve[:,0])
plt.xlabel('$t$')
plt.ylabel('$s(t)$')
plt.subplot(132)
plt.plot(t,solve[:,1])
plt.xlabel('$t$')
plt.ylabel('$v(t)$')
plt.subplot(133)
plt.plot(t,acceleration)
plt.xlabel('$t$')
plt.ylabel('$a(t)$')
plt.show()
相关文章:

姜启源数学模型第五版第五章火箭发射升空
姜启源数学模型第五版第五章例题内容复现 数学建模背景1.学习内容火箭发射升空理论知识 2.例题3.问题分析不考虑空气阻力的模型考虑空气阻力的模型 4.代码内容复现不考虑空气阻力考虑空气阻力模型 数学建模背景 首先先简单的介绍数学建模是一个怎么样的内容 数学建模是一种将数…...

局域网中电脑共享文件给手机
学习资源: 局域网共享:这样设置,你可以轻松拷贝任何电脑的文件。_哔哩哔哩_bilibili 可以实现什么效果? 连接同一个WIFI,电脑端为服务端,提供共享文件,手机是客户端,可以读取服务端…...

线段树练习
P1198 [JSOI2008] 最大数 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) // Problem: P1198 [JSOI2008] 最大数 // Contest: Luogu // URL: https://www.luogu.com.cn/problem/P1198 // Memory Limit: 128 MB // Time Limit: 1000 ms // // Powered by CP Editor (https://c…...

Mybatis映射.动态sql.分页
介绍: 动态SQL是MyBatis提供的一种动态生成SQL语句的方式,可以根据不同的条件生成不同的SQL语句,从而实现更加灵活的查询和操作。 在MyBatis的映射文件中,可以通过使用if、choose、when、otherwise、foreach等标签来实现动态SQL…...

springboot向resources下写文件的两种方式
文章目录 方式一:方式二: 方式一: import java.io.File; import java.io.FileWriter; import java.io.IOException;public class WriterFileUtils {private static final String prefix "classpath:";public static void writeFi…...

Sloare flare网卡信息
详细的安装信息 https://github.com/Xilinx-CNS/onload/tree/master/scripts 进行下载 Solarflare网卡开发:openonload 安装与调试_openonload安装_Erice_s的博客-CSDN博客 cns-sfnettest测试 cns-sfnettest 下载 https://github.com/Xilinx-CNS/cns-sfnettes…...

Redis知识点整理
第一部分:Redis基础知识点 1、数据类型 5种常用基础类型:string,hash,list,set,zset – 字符串,Hash表,List顺序集合,Set无序集合,ZSet有序集合3中特殊类型:bitmap-字节地图, hyperloglog-统计…...

React笔记(一)初识React
一、React概述 1、什么是react react的官网:React 用于构建用户界面的 JavaScript 库,它也是一个渐进式的用于构建用户界面的javascript框架 2、主要特征 声明式:使用原生JS编写的页面存在着开发效率低下、性能较差的情况,使用react大家就…...

C语言——指针进阶(一)
目录 编辑 一.字符指针 1.1 基本概念 1.2 面试题 二.指针数组 三.数组指针 3.1 数组指针的定义 3.2 &数组名VS数组名 3.3 数组指针的使用 四.数组参数、指针参数 4.1 一维数组传参 编辑 4.2 二维数组传参 4.3 一级指针传参 4.4 二级指针传参 编辑 五.…...
【ArcGIS Pro二次开发】(62):复制字段
应网友需求,做了这么一个复制字段的小工具。 假定这样一个场景,手头有一个要素1,要素里有10个字段,另一个要素2,除了shape_area等图形字段外,没有其它字段。 现在的需求是,想把要素1中的8个字…...

【Tkinter系列02/5】界面初步和布局
本文是系列文章第二部分。前文见:【Tkinter系列01/5】界面初步和布局_无水先生的博客-CSDN博客 说明 一般来说,界面开发中,如果不是大型的软件,就不必用QT之类的实现,用Tkinter已经足够,然而即便是Tkinter规…...

2023年03月 C/C++(四级)真题解析#中国电子学会#全国青少年软件编程等级考试
第1题:最佳路径 如下所示的由正整数数字构成的三角形: 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 从三角形的顶部到底部有很多条不同的路径。对于每条路径,把路径上面的数加起来可以得到一个和,和最大的路径称为最佳路径。你的任务就是求出最佳路径上的…...

介绍一些编程语言— CSS 语言
介绍一些编程语言— CSS 语言 CSS 语言 简介 CSS,层叠样式表,是一种用来表现 HTML 或 XML 等文件样式的计算机语言。CSS 不仅可以静态地修饰网页,还可以配合各种脚本语言动态地对网页各元素进行格式化。 CSS 能够对网页中元素位置的排版进…...

一文讲清楚c/c++中的宏
一文讲清楚c/c中的宏 文章目录 一文讲清楚c/c中的宏一、如何理解这个“宏”字面的意思呢?二、c/c中的宏详解三、宏的使用场景 一、如何理解这个“宏”字面的意思呢? 在刚开始学习C语言的时候,始终有点分不清楚"宏"这个字面上的意思…...

typescript进阶语法
typescript进阶语法 interface 接口定义 interface userType {name:string,age:number,sex?:string }type接口定义 type userType {name:string,age:number,sex?:string } type userType username # 固定值写法 let user:userType age # 报错 只能等于usernamepick摘取…...

宝塔终端 查看 7003端口 占用 并且杀死
要查看端口是否被占用并杀死相关进程,你可以按照以下步骤执行: 打开宝塔面板,进入服务器管理页面。在左侧导航栏中选择「工具」,然后选择「终端」进入宝塔终端界面。输入以下命令查看端口占用情况:netstat -tuln | gr…...

可解释性的相关介绍
一、可解释性的元定义(Meta-definitions of Interpretability) The extent to which an individual can comprehend the cause of a model’s outcome. [1]The degree to which a human can consistently predict a model’s outcome. [2] 可解释性&am…...
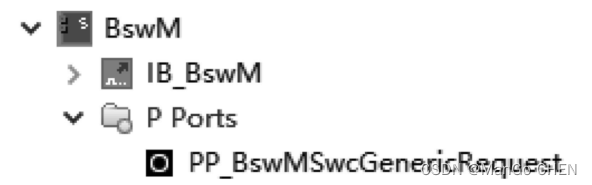
AUTOSAR规范与ECU软件开发(实践篇)6.7 服务软件组件与应用层软件组件端口连接
在生成了BSW模块的代码后, 切换到ISOLAR-A系统级设计界面,会发现产生一些基础软件模块的服务软件组件: BswM、 ComM、 Det和EcuM等, 如图6.60所示。 图6.60 生成了BSW后的服务软件组件 此时, 如果涉及服务软件组件与应用层软件组件的交互, 就需要为应用层软件组…...
:列表)
菜鸟教程《Python 3 教程》笔记(6):列表
菜鸟教程《Python 3 教程》笔记(6) 6 列表6.1 删除列表元素6.2 列表函数和方法6.2.1 max()、min()6.2.2 reverse()6.2.3 sort() 6 列表 出处: 菜鸟教程 - Python3 列表 6.1 删除列表元素 >>> list [Google, Runoob, 1997, 2000]…...

LeetCode-56-合并区间
题目描述: 以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。 可以使用 LinkedList,…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
