Leetcode:238. 除自身以外数组的乘积【题解超详细】
纯C语言实现(小白也能看明白)
题目
给你一个整数数组
nums,返回 数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积 。题目数据 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请不要使用除法,且在
O(n)时间复杂度内完成此题。难度:中等
题目链接:238. 除自身以外数组的乘积
解题思路
由于该题不能使用除法 所以参考题解写一个左右乘积列表的方法 创建两个新的数组a,b 一个用于记录从左到右的乘积(类似于动态规划的思想)a 另一个记录从右到左的乘积 b(注意b是从右到左进行累乘) 而a的最左端为1,b的最右端为1 如此在结尾的时候只需要a*b即可 举例, ans[0]=a[0]*b[0] a[0]=1 b[0]=除了nums[0]以外所有元素的乘积
代码展示
/*** Note: The returned array must be malloced, assume caller calls free().*/
int* productExceptSelf(int* nums, int numsSize, int* returnSize){//前缀积*后缀积 == 除自身以外数组的乘积int *answer = (int*)malloc(sizeof(int)*numsSize);answer[0] = 1;//第一个数字前面没有数字了,第一个数字的前缀是1int i = 0;//前缀积for(i = 1;i<numsSize;i++){answer[i] = answer[i-1]*nums[i-1];}//后缀积int rp[numsSize];//用来记录后缀积rp[numsSize-1] = 1;//因为最后边的数的后缀只能是1for(i = numsSize -1-1;i>=0;i--){rp[i] = rp[i+1] * nums[i+1]; }for(i = 0;i<numsSize;i++){answer[i] = answer[i] * rp[i];//前缀积*后缀积}*returnSize = numsSize;//返回数组的大小return answer;//返回数组answer
}【超详细解析】
首先这是一个函数功能实现,一定要注意函数的参数。(int * nums ,这是传的是数组的地址,numsSize,这是数组的大小,*numsSize ,是要返回使用后数组的大小)
接下来是 代码分析
因为 根据题目的意思 我们要返回数组answer ,可以使用malloc()动态分配内存空间
int *answer = (int*)malloc(sizeof(int)*numsSize);
这行代码的意思是:创建了一个指针变量 answer,并使用 malloc() 函数动态分配了一块内存空间,大小为 sizeof(int)*numsSize 字节。其中,sizeof(int) 是指 int 类型在当前系统中所占据的字节数,numsSize 是一个变量,表示需要分配的元素个数。通过将 malloc() 返回的内存地址强制类型转换为 int*,将其赋值给指针变量 answer。这样就可以在动态分配的内存空间中存储 numsSize 个整数。
题目的意思 计算除自身以外数组的乘积,我们根据解题思路,采用 结果 == 前缀积 * 后缀积
就比如 1 2 3 4 5,这里 我采取除3以外数组的乘积(1*2*4*5),因为题目要求不要使用除法,且在 O(n) 时间复杂度内完成此题。所以 (1*2*4*5)变为 1*2 ( 前缀积) * 4*5(后缀积),
这样 (1*2)*(4*5)
前缀积
这里我们以数组 [1,2,3,4] , 这里我们需要注意的是 数组的第一个元素的前缀乘积和数组的最后一个元素的后缀乘积是1。我们用answer数组来接收
answer[0] = 1;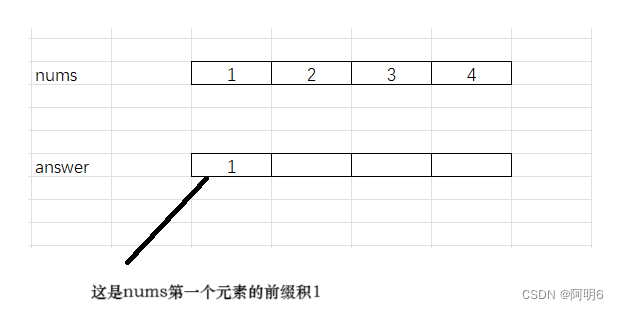
(虽然answer数组要返回结果,我们可以先使用得到前缀之积,再借助另一个数组得到后缀之积,然后两数组各个元素相乘得到结果。这样就可一个减少一定的内存消耗)
接下里求前缀积(因为我们知道数组第一个元素的前缀之积是1)故从第二个元素开始计算
//前缀积for(i = 1;i<numsSize;i++){answer[i] = answer[i-1]*nums[i-1];}接下来要求的是nums[1] 即第二个元素的前缀积
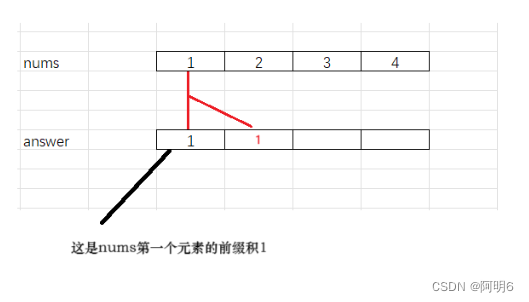
因为nums[1] 前面只有一个元素就是 1 故nums[1] 的前缀积 是1
再看nums[2]
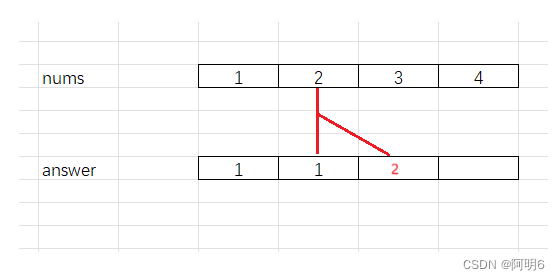
这时你可能有这样的疑问 为什么要 nums[1]*answer[1] 而不是 nums[0] * nums[1] 呢
这里你需要知道 乘积 肯定时连乘的 ,可以这样理解 answer数组 里面存放 的每一个阶段的乘积(其实就是每个nums数组对应的前缀的乘积)
nums[3]
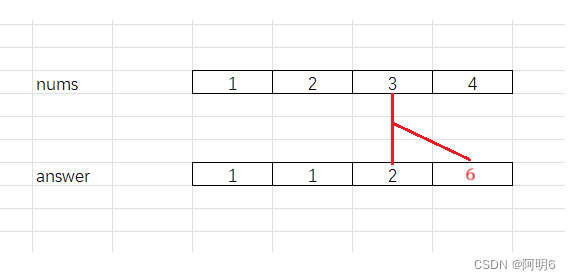
后缀乘积
//后缀积int rp[numsSize];//用来记录后缀积rp[numsSize-1] = 1;//因为最后边的数的后缀只能是1for(i = numsSize -1-1;i>=0;i--){rp[i] = rp[i+1] * nums[i+1]; }这提前声明了一个rp数组用来记录后缀积,数组最后的一个元素的后置缀之积 是1
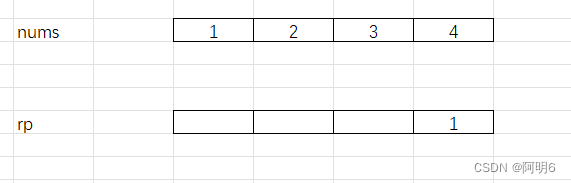
rp[1]
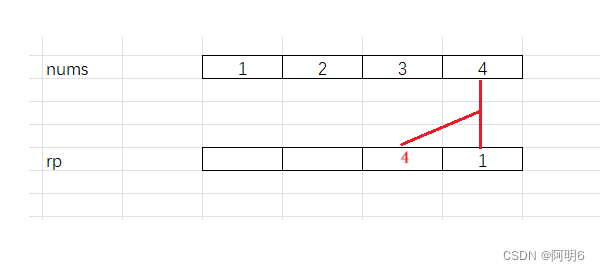
rp[2]
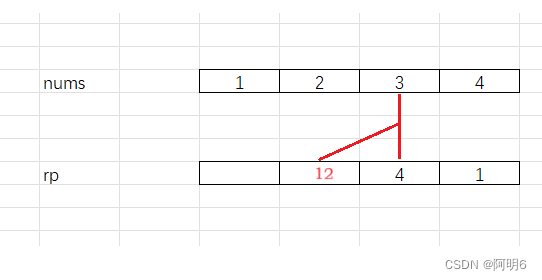
rp[3]

前缀积*后缀积
for(i = 0;i<numsSize;i++){answer[i] = answer[i] * rp[i];//前缀积*后缀积}最后 answer数组与rp数组对应元素做乘积(answer[i] = answer[i] * rp[i])
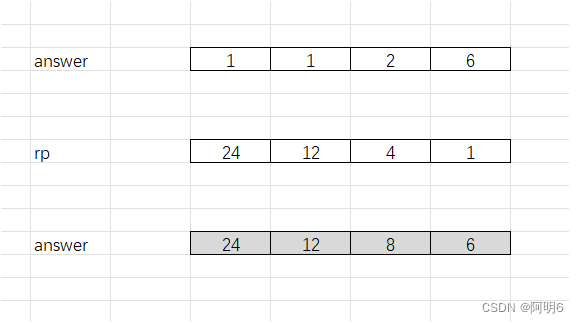
这的answer数组的大小与 nums 的数组大小一致 返回 numsSize ,数组返回 answer

相关文章:

Leetcode:238. 除自身以外数组的乘积【题解超详细】
纯C语言实现(小白也能看明白) 题目 给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数…...
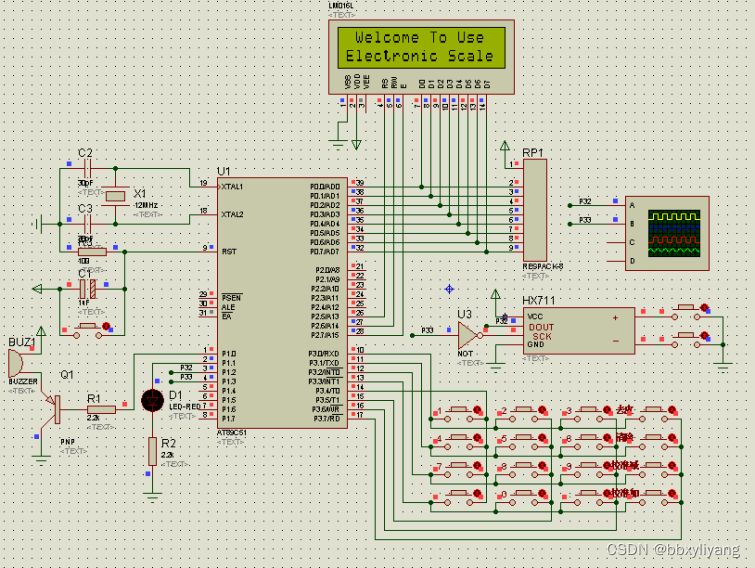
基于单片机的智能数字电子秤proteus仿真设计
一、系统方案 1、当电子称开机时,单片机会进入一系列初始化,进入1602显示模式设定,如开关显示、光标有无设置、光标闪烁设置,定时器初始化,进入定时器模式,如初始值赋值。之后液晶会显示Welcome To Use Ele…...

大数据(二)大数据行业相关统计数据
大数据(二)大数据行业相关统计数据 目录 一、大数据相关的各种资讯 二、转载自网络的大数据统计数据 2.1、国家大数据政策 2.2、产业结构分析 2.3、应用结构分析 2.4、数据中心 2.5、云计算 一、大数据相关的各种资讯 1. 据IDC预测࿰…...
Ruoyi安装部署(linux环境、前后端不分离版本)
目录 简介 1 新建目录 2 安装jdk 2.1 jdk下载 2.2 解压并移动文件夹到/data/service目录 2.3 配置环境变量 3 安装maven 3.1 进入官网下载最新的maven 3.2 解压并移动文件夹到/data//service目录 3.3 配置环境变量 3.4 配置本地仓库地址与阿里云镜像 4 安装git 4.…...
PHP聚合支付网站源码/对接十多个支付接口 第三方/第四方支付/系统源码
PHP聚合支付网站源码/对接十多个支付接口 第三方/第四方支付/系统源码 内附数十个支付接口代码文件。 下载地址:https://bbs.csdn.net/topics/616764485...
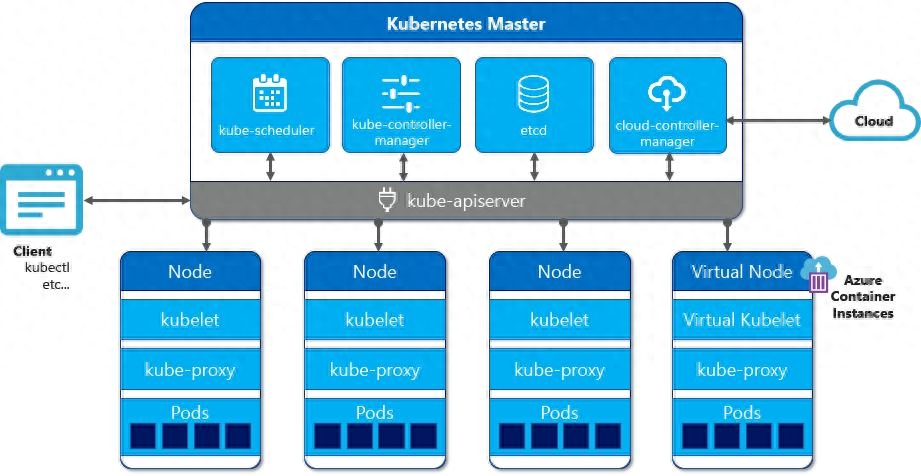
容器化微服务:用Kubernetes实现弹性部署
随着云计算的迅猛发展,容器化和微服务架构成为了构建现代应用的重要方式。而在这个过程中,Kubernetes(常简称为K8s)作为一个开源的容器编排平台,正在引领着容器化微服务的部署和管理革命。本文将深入探讨容器化微服务的…...
DevOps系列文章 之 Python基础
Python语法结构 语句块缩进 1.python代码块通过缩进对齐表达代码逻辑而不是使用大括号 2.缩进表达一个语句属于哪个代码块 3.缩进风格 : 建议使用四个空格 如果是Linux系统的话,可以这样做,实现自动缩进 : vim ~/.vimrc set ai…...

Harbour.Space Scholarship Contest 2023-2024 (Div. 1 + Div. 2) A ~ D
比赛链接 A 正常枚举就行,从最后一位往前枚举,-1、-2、-3...这样 #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \nusing namespace std;typedef pair<int, int> PII; typedef long l…...
[管理与领导-53]:IT基层管理者 - 8项核心技能 - 8 - 持续改进
前言: 管理者存在的价值就是制定目标,即目标管理、通过团队(他人)拿到结果。 要想通过他人拿到结果: (1)目标:制定符合SMART原则的符合业务需求的目标,团队跳一跳就可以…...
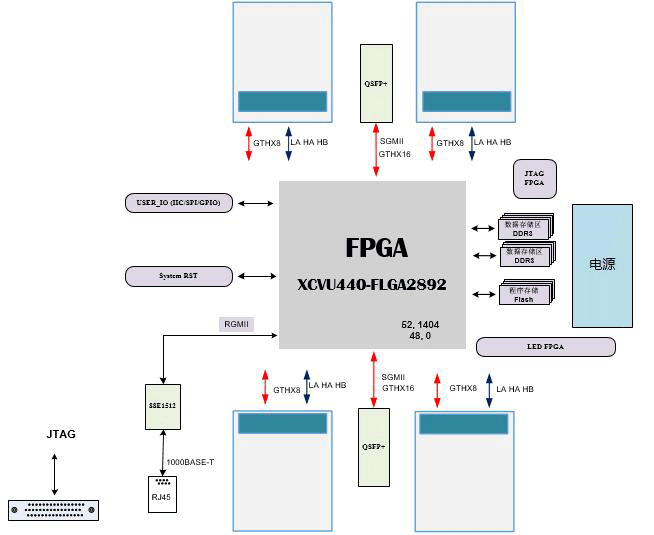
芯片验证板卡设计原理图:446-基于VU440T的多核处理器多输入芯片验证板卡
基于VU440T的多核处理器多输入芯片验证板卡 一、板卡概述 基于XCVU440-FLGA2892的多核处理器多输入芯片验证板卡为实现网络交换芯片的验证,包括四个FMC接口、DDR、GPIO等,北京太速科技芯片验证板卡用于完成甲方的芯片验证任务,多任务…...

几个nlp的小任务(机器翻译)
几个nlp的小任务(机器翻译) 安装依赖库数据集介绍与模型介绍加载数据集看一看数据集的样子评测测试数据预处理测试tokenizer处理目标特殊的token预处理函数对数据集的所有数据进行预处理微调预训练模型设置训练参数需要一个数据收集器,把处理好数据喂给模型设置评估方法参数…...
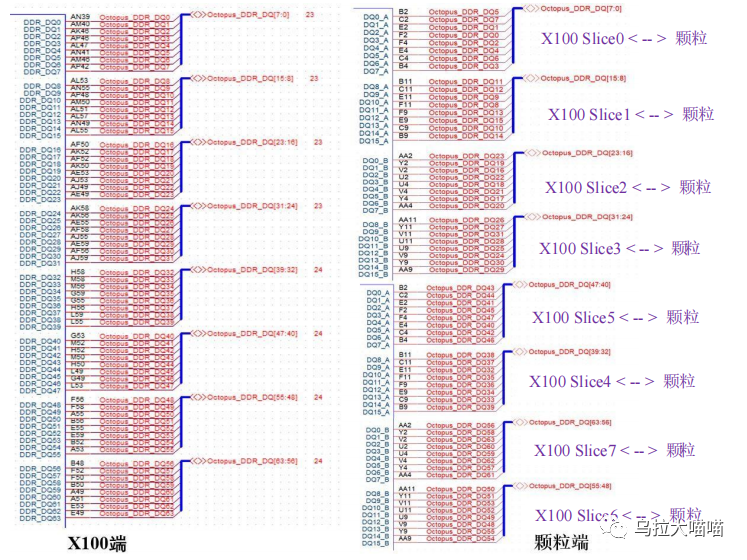
飞腾X100 LPDDR颗粒线序配置辅助工具
B站讲解视频: 正文内容: 一、 飞腾X100显存使用LPDDR4时,需要工程师在X100的固件中去配置线序交换说明,就类似下面这个: 图1 我们需要输入每个slice中DQ的线序,也需要输入slice之间的交换关系,这个工作量也不小,同时容易出现错误,所以开发了一款辅助小工具,…...
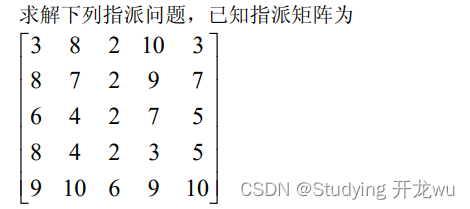
二、数学建模之整数规划篇
1.定义 2.例题 3.使用软件及解题 一、定义 1.整数规划(Integer Programming,简称IP):是一种数学优化问题,它是线性规划(Linear Programming,简称LP)的一个扩展形式。在线性规划中&…...

C语言日常刷题 4
文章目录 题目答案与解析123456 题目 1、设变量已正确定义,以下不能统计出一行中输入字符个数(不包含回车符)的程序段是( ) A: n0;while(chgetchar()!‘\n’)n; B: n0;while(getchar()!‘\n’)n; C: for(n0;getchar()…...
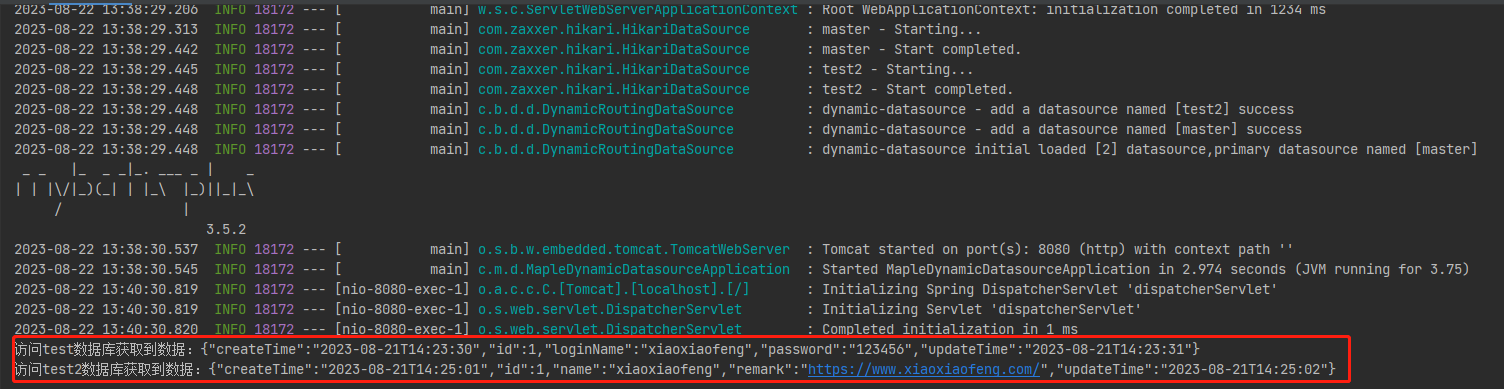
MyBatis plus 多数据源实现
1. 项目背景 最近写文章发布到【笑小枫】小程序和我的个人网站上,因为个人网站用的是halo框架搭建,两边数据结构不一致,导致我每次维护文章都需要两边维护,这就很烦~ 于是,本文就诞生了。通过项目连接这两个数据库&a…...

k-近邻算法概述,k-means与k-NN的区别对比
目录 k-近邻算法概述 k-近邻算法细节 k值的选取 分类器的决策 k-means与k-NN的区别对比 k-近邻算法概述 k近邻(k-nearest neighbor, k-NN)算法由 Cover 和 Hart 于1968年提出,是一种简单的分类方法。通俗来说,就是给定一个…...

node 项目搭建
1. 初始化项目 cmd 执行 cnpm init -y 创建README.md 依赖安装 1. 数据库 和 框架 mysql express cnpm install mysql express --save 2. 后端跨域 cors cnpm i cors 3. 安装 body-parser 声明引用 用于接收前端 post 过来的数据 cnpm install --save body-parser 4…...
CSS 属性值计算过程
目录 例子1,确定声明值2,层叠冲突2.1,比较源重要性2.2,比较优先级2.3,比较源次序 3,使用继承4,使用默认值其他 例子 我们来举例说明<h1> 标签最终的样式: <div><h1…...

QT版权查询
文章目录 QT工具版权QT模块版权查询 根据条件自动筛选: Qt Features, Framework Essentials, Modules, Tools & Add-Ons QT工具版权 Licensing QT模块版权查询 在 All Modules 中点击进入每个模块,在详细内容中一般有Lisence相关内容。 Licens…...

【leetcode 力扣刷题】双指针///原地扩充线性表
双指针///原地扩充线性表 剑指 Offer 05. 替换空格定义一个新字符串扩充字符串,原地替换思考 剑指 Offer 05. 替换空格 题目链接:剑指 Offer 05. 替换空格 题目内容: 这是一道简单题,理解题意,就是将字符串s中的空格…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
