ADRC自抗扰控制总结
目录
前言
1.ADRC形式
1.1形一
1.2形二
2.被控对象
3.仿真分析
3.1仿真模型
3.2仿真结果
4.学习问题
前言
前面的3篇文章依次介绍了微分跟踪器TD、状态观测器ESO和非线性状态误差反馈NLSEF三部分内容,至此ADRC的结构已经介绍完毕,现在对分块学习的内容进行整合,并进行实例仿真分析,ADRC分解学习博客链接:
自抗扰控制ADRC之三种微分跟踪器TD仿真分析_Mr. 邹的博客-CSDN博客
自抗扰控制ADRC之扩张观测器_Mr. 邹的博客-CSDN博客
自抗扰控制ADRC之反馈控制律(NLSEF)_Mr. 邹的博客-CSDN博客
1.ADRC形式
由于反馈控制的形式有两种,所以对应的ADRC有两种,
1.1形一
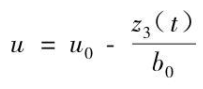
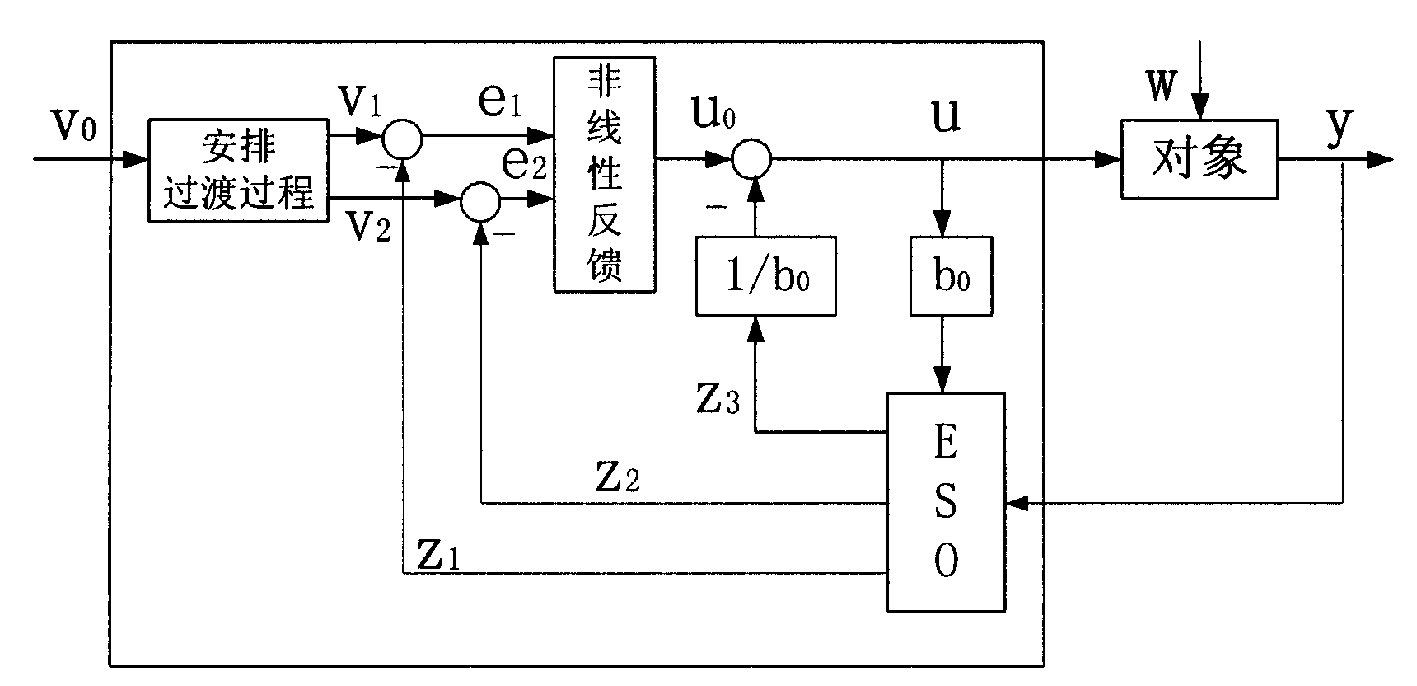
1.2形二

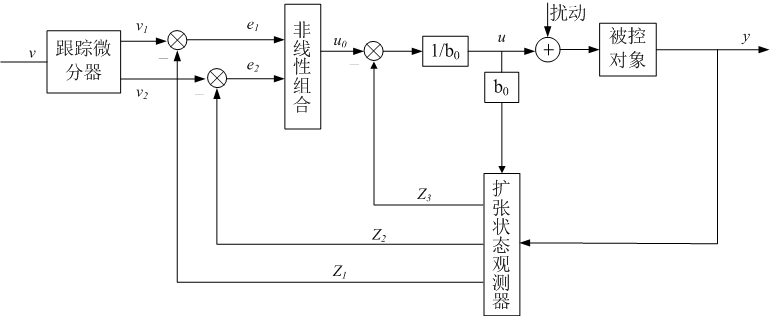
注:
①如果未将b0写入扩张观测器内部,则传入控制ESO的u要乘b0(上述两图便展示如此);如果将b0写入扩张观测器内部,则传入控制ESO的u不需要乘b0,这是很容易误导的一个地方。所以有的文献中也会构建不要b0传入ESO:
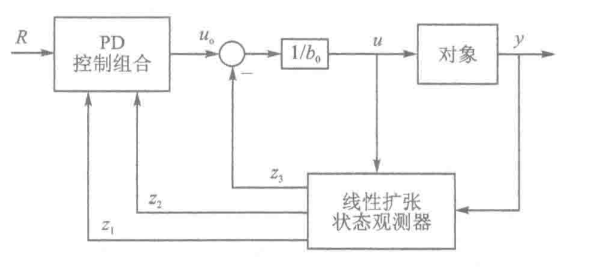
②为什么有的地方直接将b0写成b?是因为大多数情况系统若不考虑参数b的摄动,相当于已知b,所以将b代替b0可以补偿和估计的更为准确。
2.被控对象
取f = -25x2+33sin(Πt),b=133。
3.仿真分析
3.1仿真模型
微分跟踪器:Levant
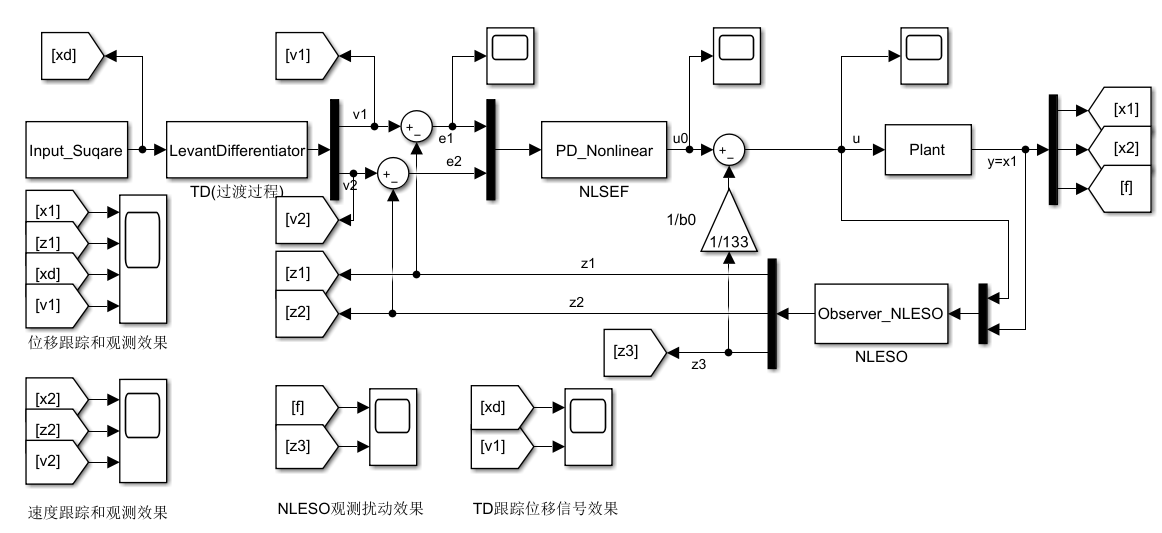
3.2仿真结果
以方波作为输入,其仿真效果如下所示:
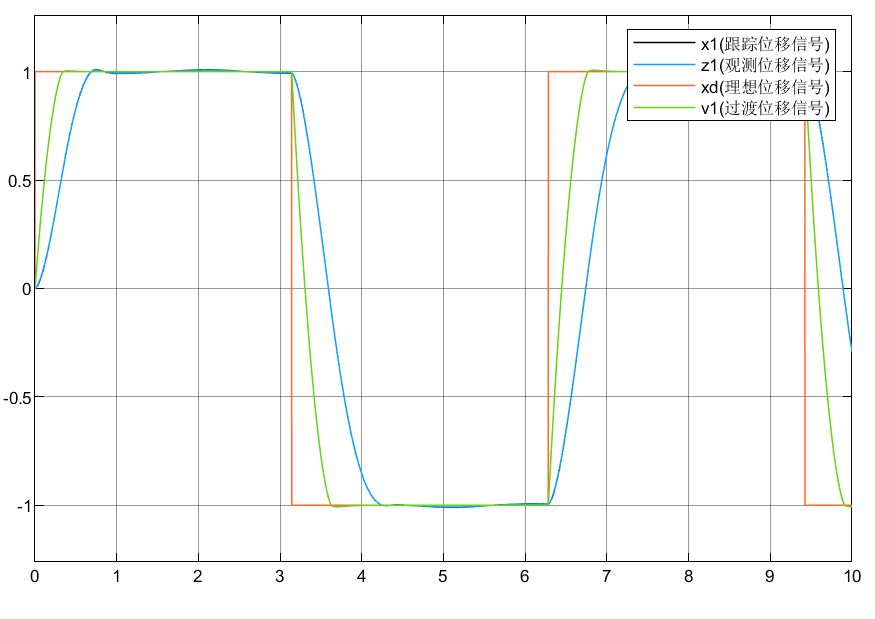
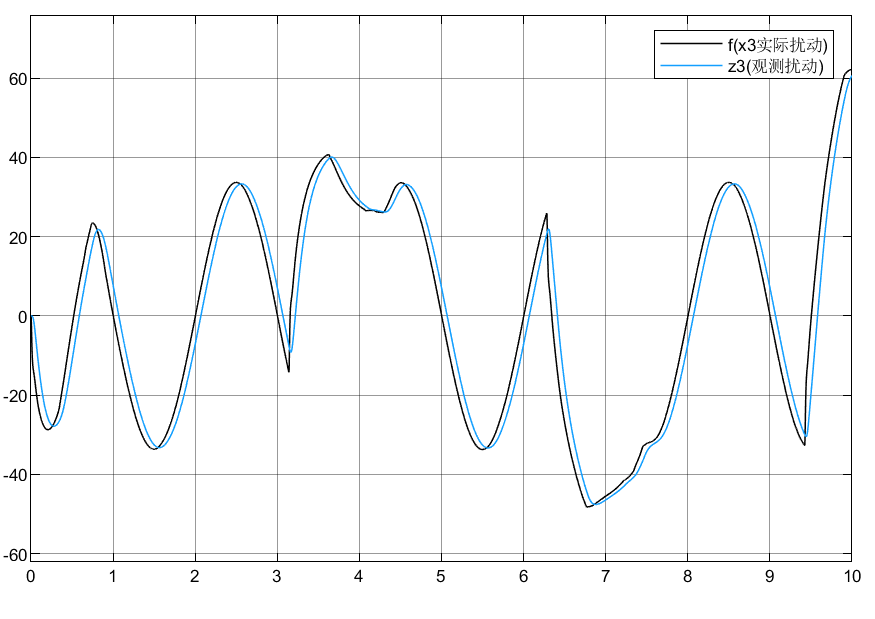
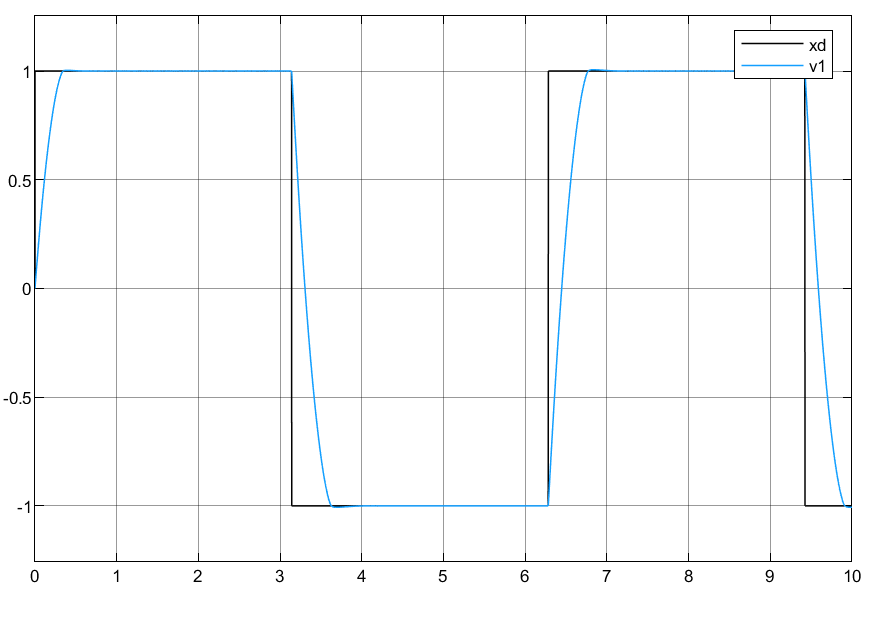
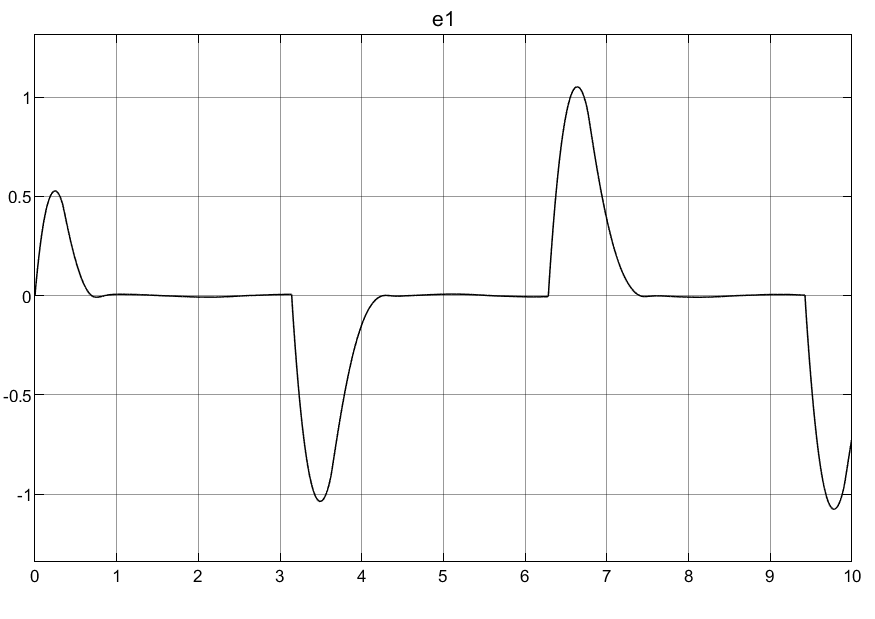
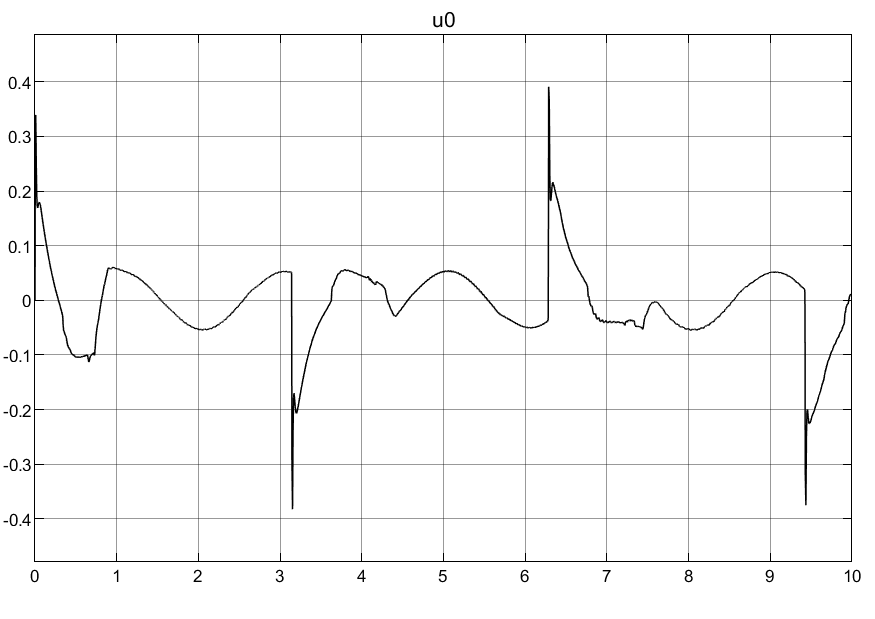
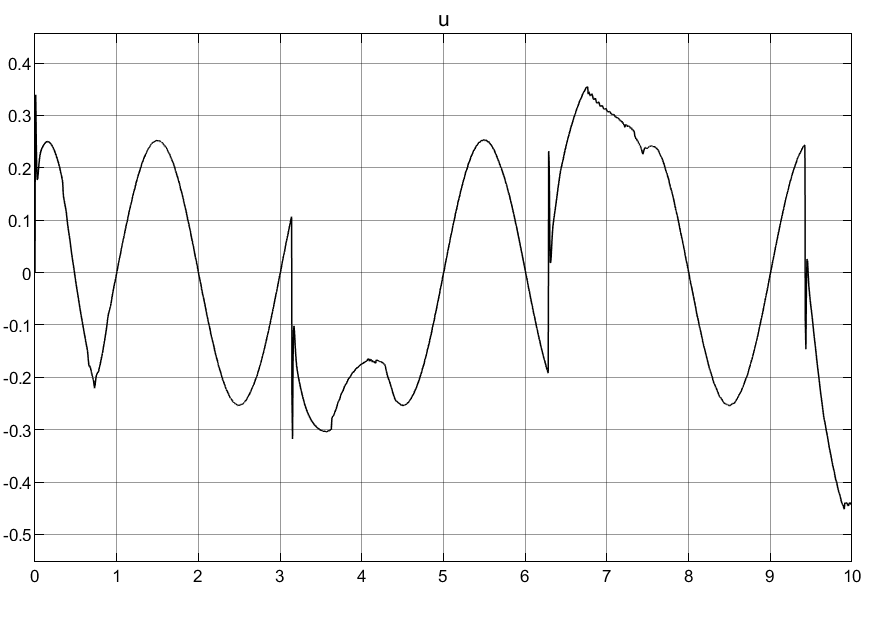
4.学习问题
①参数的调节还没学到位,后续还需学习总结;
②实际上跟踪的效果并不算很好;
③非线性观测器的效果并非很好;
④误差变化律e2的跟踪非常差,在滑模控制中很少出现:
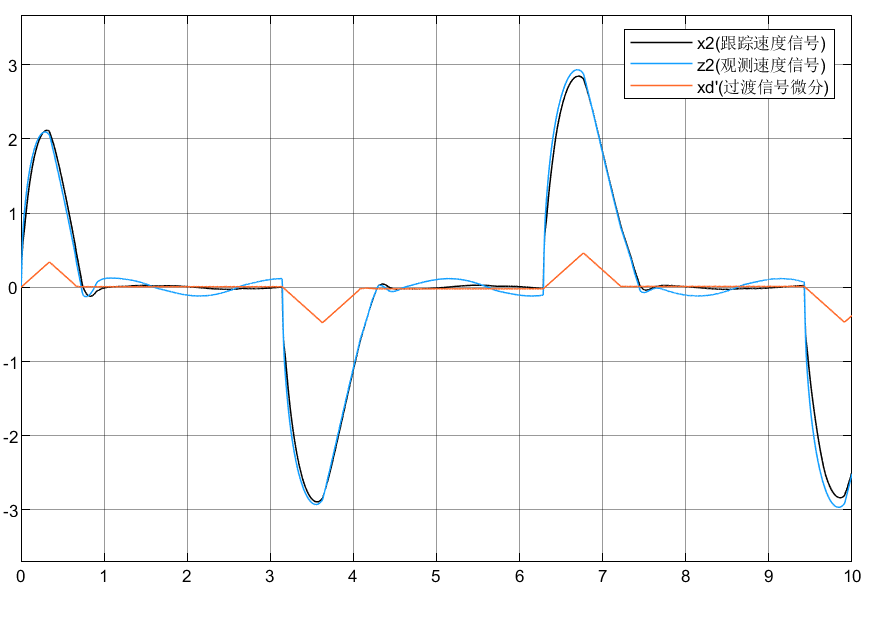
相关文章:

ADRC自抗扰控制总结
目录 前言 1.ADRC形式 1.1形一 1.2形二 2.被控对象 3.仿真分析 3.1仿真模型 3.2仿真结果 4.学习问题 前言 前面的3篇文章依次介绍了微分跟踪器TD、状态观测器ESO和非线性状态误差反馈NLSEF三部分内容,至此ADRC的结构已经介绍完毕,现在对分块学习…...
3年工作之后是不是还在“点点点”,3年感悟和你分享....
经常都有人问我软件测试前景怎么样,每年也都帮助很多朋友做职业分析和学习规划,也很欣慰能够通过自己的努力帮到一些人进入到大厂。 2023年软件测试行业的发展现状以及未来的前景趋势 最近很多测试人在找工作的时候,明显的会发现功能测试很…...
【自动化测试】web自动化测试验证码如何测?如何处理验证码问题?解决方案......
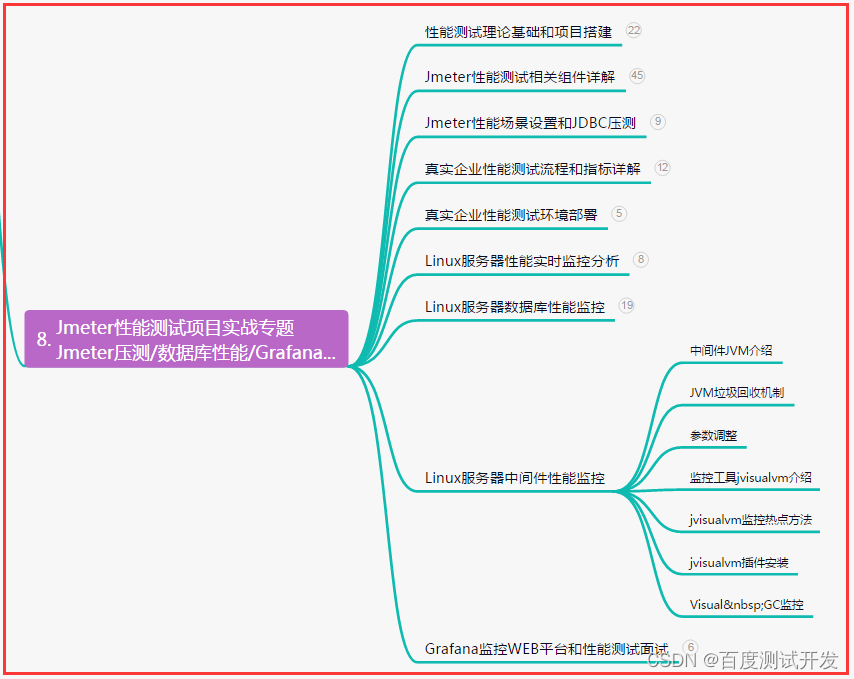
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 在对安全性有要求的…...
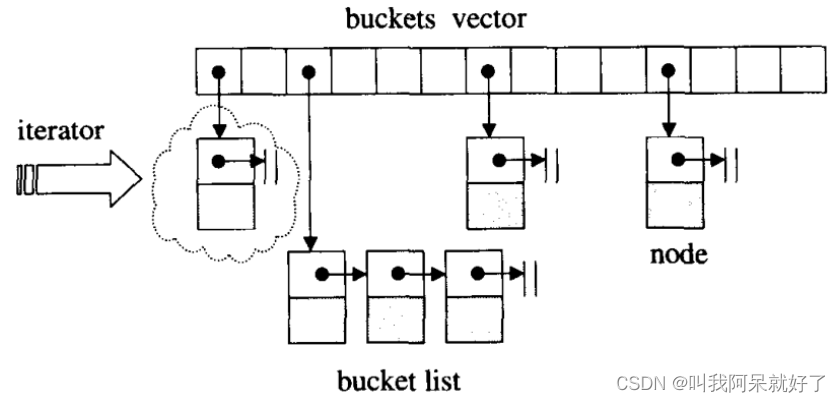
面试浅谈之 C++ STL 篇
面试浅谈之 C STL 篇 一 🏠 概述 HELLO,各位博友好,我是阿呆 🙈🙈🙈 这里是面试浅谈系列,收录在专栏面试中 😜😜😜 本系列将记录一些阿呆个人整理的面试题…...
)
【PTA Advanced】1144 The Missing Number(C++)
目录 题目 Input Specification: Output Specification: Sample Input: Sample Output: 思路 代码 题目 Given N integers, you are supposed to find the smallest positive integer that is NOT in the given list. Input Specification: Each input file contains…...

oracle的sqlnet.ora文件配置传输加密算法
sqlnet.ora文件位于ORACLE_HOME/network/admin目录中。sqlnet.ora文件中增加如下:SQLNET.ENCRYPTION_SERVER REQUIRED SQLNET.ENCRYPTION_TYPES_SERVER (RC4_256) SQLNET.CRYPTO_CHECKSUM_SERVER REQUIRED SQLNET.CRYPTO_CHECKSUM_TYPES_SERVER MD5SQLNET.ENCRYP…...
RK3568存储性能测试
USBU盘储存性能参数(USB3.0接口)参数测试条件最小典型最大单位说明写速度写入1GB数据—32.6—MB/sU盘型号:KODAK,32GB USB3.0读速度读取1GB数据—66.7—MB/s 备注HW356X-CORE-4GB-32GBHW356X-GKA,操作系统:LinuxU盘储存性能参数(U…...
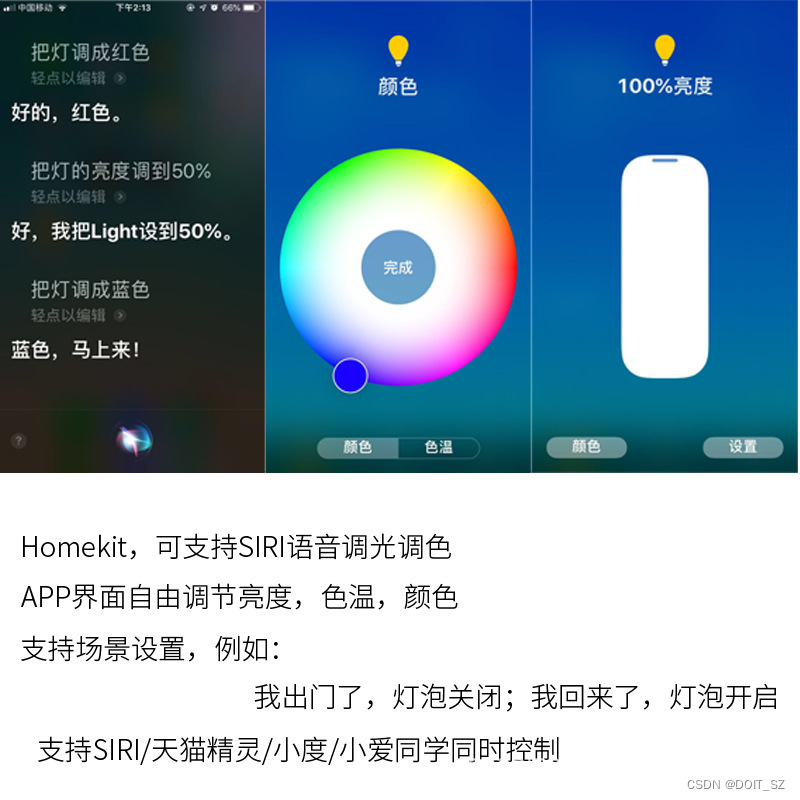
Homekit智能家居一智能灯泡
一、什么是智能灯 传统的灯泡是通过手动打开和关闭开关来工作。有时,它们可以通过声控、触控、红外等方式进行控制,或者带有调光开关,让用户调暗或调亮灯光。 智能灯泡内置有芯片和通信模块,可与手机、家庭智能助手、或其他智能…...
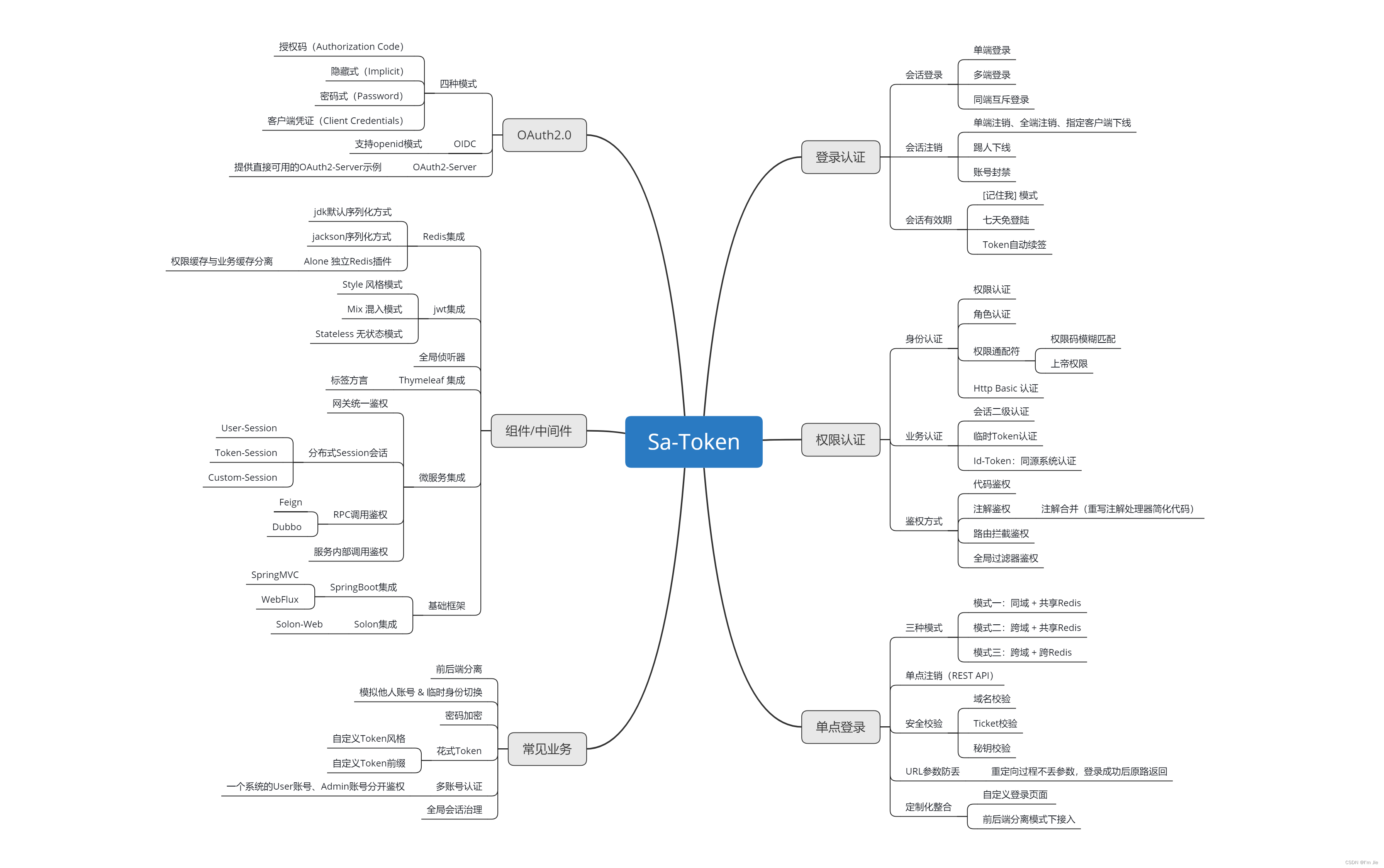
轻量级 Java 权限认证框架——Sa-Token
文章目录Sa-Token 介绍SpringBoot 集成 Sa-TokenSa-Token 功能登录认证会话查询Token 查询权限认证权限校验角色校验注解鉴权注册 Sa-Token 拦截器关闭注解校验路由拦截鉴权注册 Sa-Token 路由拦截器[记住我] 模式密码加密Sa-Token 集成 Redis方式1、使用 jdk 默认序列化方式方…...
)
算法复习(四、五、六)
动态规划 动态规划算法的有效性依赖于问题本身所具有的两个重要性质:最优子结构、重叠子问题 关于动态规划算法和备忘录方法的适用条件: 要求: 用分治法和动态规划法分别解决最大子段和问题(第四步求最优解不需要掌握ÿ…...
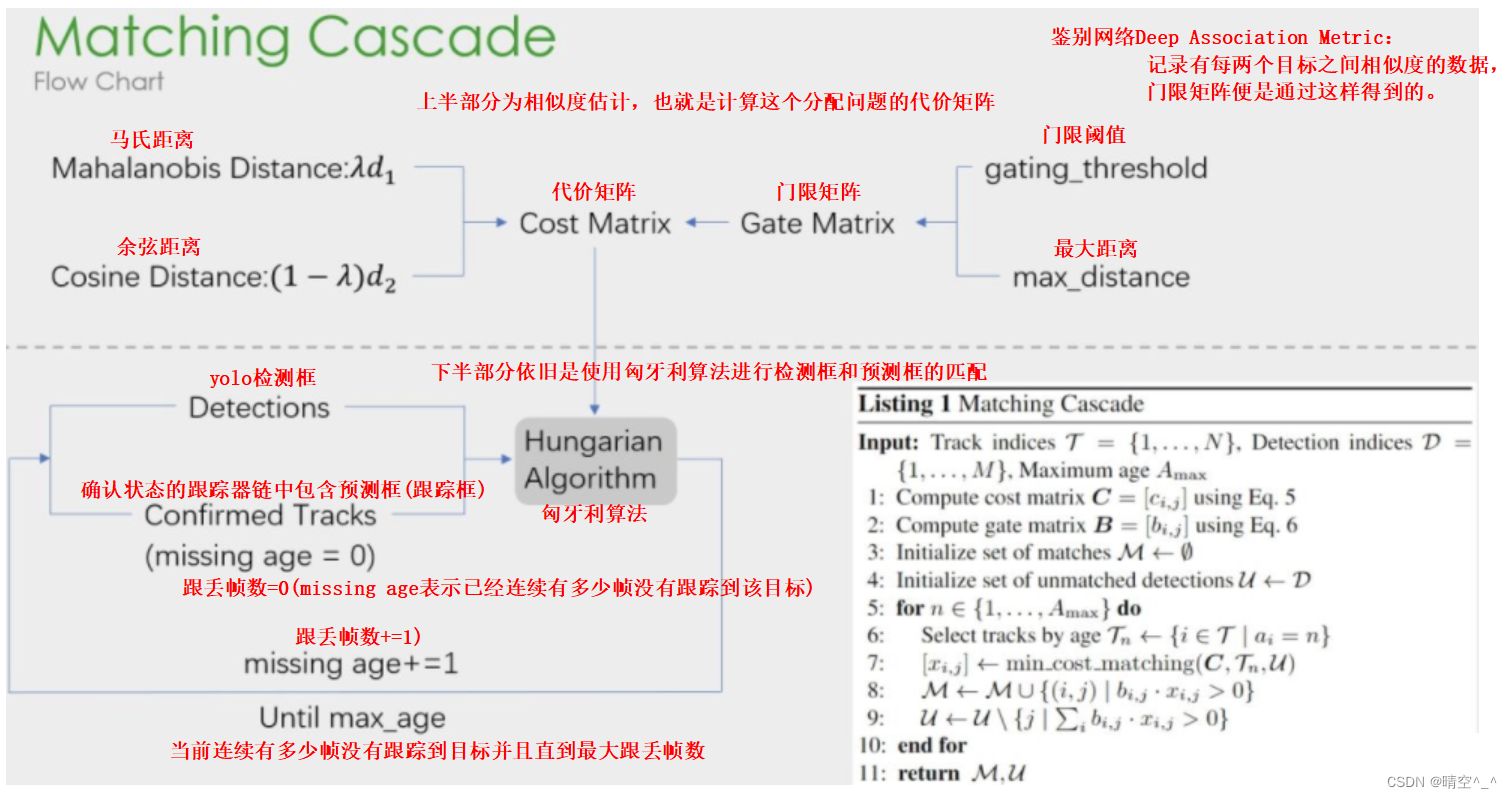
SORT与DeepSORT简介
一、MOT( mutil-object tracking)步骤 在《DEEP LEARNING IN VIDEO MUTIL-OBJECT TEACKING: A SURVEY》这篇基于深度学习多目标跟踪综述中,描绘了MOT问题的四个主要步骤 1.跟定视频原始帧 2.使用目标检测器如Faster-rcnn, YOLO, SSD等进行检测,获取目标…...
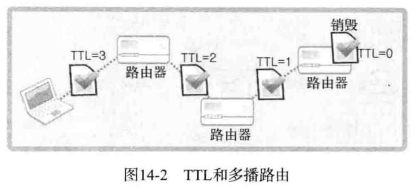
TCP/IP网络编程——多播与广播
完整版文章请参考: TCP/IP网络编程完整版文章 文章目录第 14 章 多播与广播14.1 多播14.1.1 多播的数据传输方式以及流量方面的优点14.1.2 路由(Routing)和 TTL(Time to Live,生存时间),以及加入组的办法14…...

K8S DNS解析过程和延迟问题
一、Linux DNS查询解析原理(对于调用glibc库函数gethostbyname的程序)我们在浏览器访问www.baidu.com这个域名,dns怎么查询到这台主机呢? 1、在浏览器中输入www.baidu.com域名,操作系统会先查找本地DNS解析器缓存&a…...
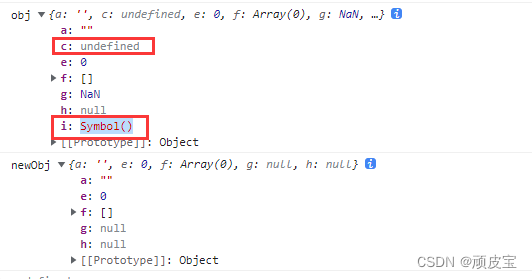
【JavaScript】js实现深拷贝的方法
前言 在js中我们想要实现深拷贝,首先要了解深浅拷贝的区别。 浅拷贝:只是拷贝数据的内存地址,而不是在内存中重新创建一个一模一样的对象(数组) 深拷贝:在内存中开辟一个新的存储空间,完完全全…...

RK3288 GPIO记录
1、引脚对应的GPIO 编号第一种 使用/sys/kernel/debug/gpio查询所有gpio引脚的基数第二种 cat /sys/class/gpio/gpiochip248/label对应的label就是GPIO引脚,例如下图GPIO8对应的基数就是2482、计算编号编号 基数 PIN脚如GPIO8的基数是248, GPIO8_A6的编…...
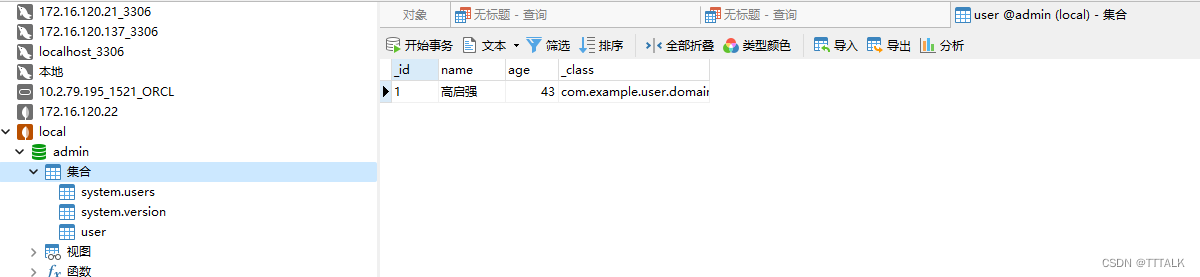
MongoDB介绍及使用教程
文章目录一、MongoDB介绍1. 什么是MongoDB2. 为什么要用MongoDB3. MongoDB的应用场景4. MongoDB基本概念二、MongoDB使用教程1.下载安装(Windows)2.MongoDB Conpass简单使用(选学)3.使用navicat连接MongoDB4.JAVA项目中使用MongoD…...

51单片机开发环境搭建 - VS Code 从编写到烧录
我安装并测试成功的环境: 操作系统:Windows 10 (22H2)单片机:STC89C52RCPython version: 3.7.6 在这之前,给51单片机写程序是用 Keil 5(编写编译)、STC-ISP(烧录),由于…...

python datetime、字符串和时间戳之间的相互转换12小时制和24小时制时间相互转化
文章目录1.字符串转datetime格式2.datetime转字符串3.时间戳转datetime格式4.datetime格式转时间戳5.应用:将12小时制的字符串转换为时间戳1.字符串转datetime格式 把字符串转换为datetime的格式 项目字符串的样子‘%m/%d/%Y %H:%M:%S’2/3/2023 15:30:20‘%m-%d-…...

百度百科词条怎么做?百度百科词条创建攻略分享
只要是想要将自己宣传出去的企业或是个人,都建议创建属于自己的百度百科词条,因为百度百科词条流量大、权重高、排名靠前,创建百度百科词条可以提高企业或是个人的知名度和口碑。 百度百科词条怎么做?每天都有用户在百度上搜索这…...
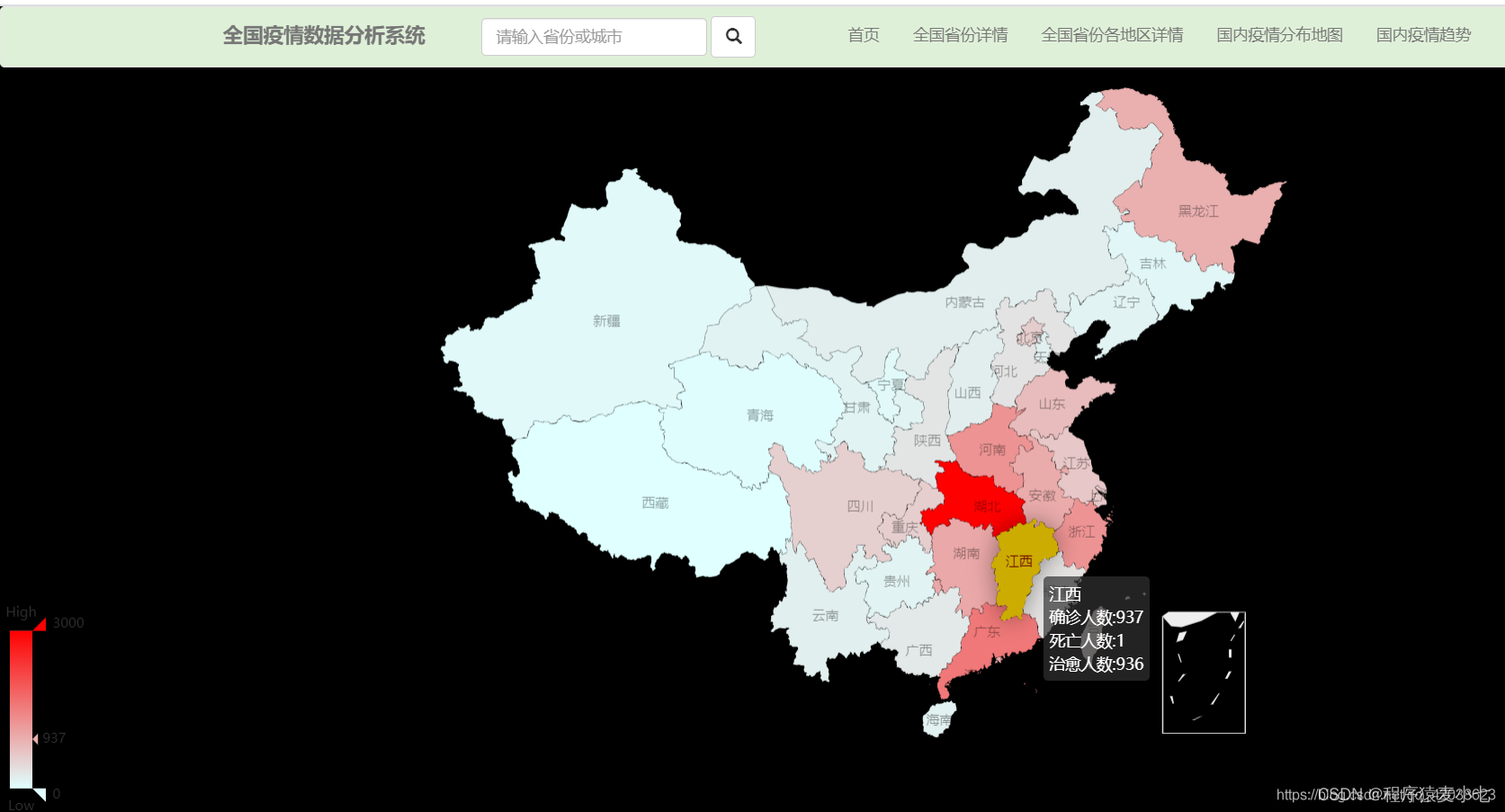
基于Hive的河北新冠确诊人数分析系统的设计与实现
项目描述 临近学期结束,还是毕业设计,你还在做java程序网络编程,期末作业,老师的作业要求觉得大了吗?不知道毕业设计该怎么办?网页功能的数量是否太多?没有合适的类型或系统?等等。这里根据疫情当下,你想解决的问…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

第22节 Node.js JXcore 打包
Node.js是一个开放源代码、跨平台的、用于服务器端和网络应用的运行环境。 JXcore是一个支持多线程的 Node.js 发行版本,基本不需要对你现有的代码做任何改动就可以直接线程安全地以多线程运行。 本文主要介绍JXcore的打包功能。 JXcore 安装 下载JXcore安装包&a…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
