算法复习(四、五、六)
动态规划
动态规划算法的有效性依赖于问题本身所具有的两个重要性质:最优子结构、重叠子问题
关于动态规划算法和备忘录方法的适用条件:
要求:
用分治法和动态规划法分别解决最大子段和问题(第四步求最优解不需要掌握)
掌握用动态规划法解决0-1背包问题
最长单调递增子序列
最长公共子序列(会写出计算最长公共子序列长度的递推式即可)
矩阵连乘问题
备忘录做法:
signed main()
{cin>>n;for(int i=0;i<=n;i++) for(int j=0;j<=n;j++) dp[i][j]=inf;for(int i=1;i<=n;i++) dp[i][i]=0;for(int i=1;i<=n;i++)cin>>row[i]>>col[i];for(int i=1;i<=n;i++) p[i]=col[i];p[0]=row[1];for(int len=2;len<=n;len++){for(int i=1;i<=n-len+1;i++){int j=i+len-1;dp[i][j]=dp[i+1][j]+p[i-1]*p[i]*p[j];s[i][j]=i;for(int k=i+1;k<j;k++){int tmp=dp[i][k]+dp[k+1][j]+p[i-1]*p[k]*p[j];if(tmp<dp[i][j]){dp[i][j]=tmp;s[i][j]=k;}}}}cout<<dp[1][n]<<endl;dfs(1,n);return 0;
}
动态规划做法:
signed main()
{cin>>n;for(int i=0;i<=n;i++) for(int j=0;j<=n;j++) dp[i][j]=inf;for(int i=1;i<=n;i++) dp[i][i]=0;for(int i=1;i<=n;i++)cin>>row[i]>>col[i];for(int i=1;i<=n;i++) p[i]=col[i];p[0]=row[1];for(int len=2;len<=n;len++){for(int i=1;i<=n-len+1;i++){int j=i+len-1;dp[i][j]=dp[i][i]+dp[i+1][j]+p[i-1]*p[i]*p[j];s[i][j]=i;for(int k=i+1;k<j;k++){if(dp[i][j]>dp[i][k]+dp[k+1][j]+p[i-1]*p[k]*p[j]){dp[i][j]=dp[i][k]+dp[k+1][j]+p[i-1]*p[k]*p[j];s[i][j]=k;}}}}cout<<dp[1][n]<<endl;print(1,n);return 0;
}
最大子段和问题
法一:
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=1e3+5;
const int inf=1e18;
int n,a[N],dp[N];signed main()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];int ans=0;for(int i=1;i<=n;i++){dp[i]=max(dp[i-1]+a[i],0ll);ans=max(ans,dp[i]);}cout<<ans<<endl;return 0;
}
/*
7
-2 11 -4 13 -5 -2 -100
*/法二:
signed main()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];int ans=0,b=0;for(int i=1;i<=n;i++){if(b>0)b+=a[i];elseb=a[i];ans=max(ans,b);}cout<<ans<<endl;return 0;
}
法三:
#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
const int N=1e3+5;
const int inf=1e18;
int n,a[N],dp[N];
int dfs(int l,int r)
{if(l==r)return a[l]>0?a[l]:0;int sum=0,mid=(l+r)/2;int left=dfs(l,mid);int right=dfs(mid+1,r);int s1=0,s2=0,tmp=0;for(int i=mid;i>=l;i--){tmp+=a[i];if(s1<tmp) s1=tmp;}tmp=0;for(int i=mid+1;i<=r;i++){tmp+=a[i];if(s2<tmp) s2=tmp;}sum=s1+s2;if(left>sum) sum=left;if(right>sum) sum=right;return sum;
}
signed main()
{cin>>n;for(int i=1;i<=n;i++) cin>>a[i];cout<<dfs(1,n)<<endl;return 0;
}
/*
7
-2 11 -4 13 -5 -2 100
*/01背包问题
int n,m,f[105][N],dp[N];void fun1()
{for(int i=1;i<=n;i++) //物品i{for(int j=1;j<=m;j++) //容量j{if(j<w[i])f[i][j]=f[i-1][j];else f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+c[i]);}}cout<<f[n][m]<<endl;
}
void fun2() //逆序更新
{for(int i=1;i<=n;i++){for(int j=m;j>=w[i];j--)dp[j]=max(dp[j],dp[j-w[i]]+c[i]);}
}最长单调递增子序列
for(int i=1;i<=n;i++) cin>>a[i],dp[i]=1;for(int i=2;i<=n;i++){for(int j=1;j<i;j++){if(a[j]<=a[i])dp[i]=max(dp[i],dp[j]+1);}}cout<<dp[n]<<endl;
最长公共子序列
{cin>>s1>>s2;len1=s1.length(),len2=s2.length();s1=" "+s1,s2=" "+s2;for(int i=1;i<=len1;i++){for(int j=1;j<=len2;j++){if(s1[i]==s2[j]) dp[i][j]=dp[i-1][j-1]+1,s[i][j]=1;else{if(dp[i-1][j]>dp[i][j-1]){dp[i][j]=dp[i-1][j];s[i][j]=2;//上面}elsedp[i][j]=dp[i][j-1];s[i][j]=3;}}}cout<<dp[len1][len2]<<endl;return 0;
}
贪心算法
适合于贪心算法求解的问题具有:贪心选择性质、最优子结构性质
贪心算法可以获取到问题的局部最优解,不一定能获取到全局最优解
掌握使用贪心算法解决:活动安排问题、背包问题、最优装载问题(件数最多)、删数问题
活动安排问题
按照结束时间进行排序
int n,p[N];
struct node
{int st,ed,id;
}a[N];
bool cmp(node a,node b)
{return a.ed<b.ed;
}
signed main()
{cin>>n;for(int i=1;i<=n;i++) {cin>>a[i].st>>a[i].ed;a[i].id=i;}sort(a+1,a+n+1,cmp);p[1]=1;int ans=1,tmp=a[1].ed;for(int i=2;i<=n;i++){if(a[i].st>=tmp){tmp=a[i].ed;ans++;p[i]=1;}}cout<<ans<<endl;return 0;
}
背包问题
int n,p[N];
struct node
{int w,v;double d;
}a[N];
bool cmp(node a,node b)
{return a.d>b.d;
}
signed main()
{cin>>n>>c;for(int i=1;i<=n;i++){cin>>a[i].w>>a[i].v;a[i].d=a[i].v/a[i].w;}sort(a+1,a+n+1,cmp);int i=1;double ans=0;while(i<=n&&a[i].w<=c){c-=a[i].w;ans+=a[i].v;i++;}if(i<=n) ans+=c*a[i].d;cout<<ans<<endl;return 0;
}
最优装载问题(件数最多)
重量轻的先装,找找重量从小到大进行排序
删数问题
找到最近下降点
#include <bits/stdc++.h>
#define int long longusing namespace std;
const int N = 7e6+100;
const int mod = 998244353;
int n,k;
string s;signed main()
{cin>>s>>k;n=s.length();if(k>=n)cout<<0<<endl;else{while(k){int i;for(i=0;i<s.length()&&s[i]<=s[i+1];i++);s.erase(i,1);k--;}while(s.size()>1&&s[0]=='0')s.erase(0,1);cout<<s<<endl;}return 0;
}
/**/第六章
子集树实现素数环
const int N =1e6+5;
int n,a[N],vis[N],ans;
int check(int a,int b)
{int sum=a+b;for(int i=2;i*i<=sum;i++)if(sum%2==0)return 0;return 1;
}
void dfs(int x)
{if(x==n+1){if(check(a[1],a[n]))ans++;return;}for(int i=1;i<=n;i++){if(!vis[i]&&check(a[x-1],i)){vis[i]=1;a[x]=i;dfs(x+1);vis[i]=0;}}
}
void solve()
{cin>>n;dfs(1);cout<<ans<<endl;
}
signed main()
{solve();return 0;
}排列树实现素数环
int n,a[N],vis[N],ans;
int check(int a,int b)
{int sum=a+b;for(int i=2;i*i<=sum;i++)if(sum%2==0)return 0;return 1;
}
void dfs(int x)
{if(x==n+1){if(check(a[1],a[n]))ans++;return;}for(int i=x;i<=n;i++){swap(a[x],a[i]);if(check(a[x-1],a[x]))dfs(x+1);swap(a[x],a[i]);}
}
void solve()
{cin>>n;for(int i=1;i<=n;i++) a[i]=i;dfs(1);cout<<ans<<endl;
}
装载问题
#include <bits/stdc++.h>
#define endl '\n'
#define int long longusing namespace std;
const int N =1e6+5;
const int inf=1e18;
int n,c,a[N],b[N],ans[N],sum,bestcw;
void dfs(int x,int cw)
{if(x==n+1){if(cw>bestcw){for(int i=1;i<=n;i++)ans[i]=b[i];bestcw=cw;}return;}sum-=a[x];if(cw+a[x]<=c){b[x]=1;cw+=a[x];dfs(x+1,cw);cw-=a[x];}if(cw+sum>bestcw){b[x]=0;dfs(x+1,cw);}sum+=a[x];
}
void solve()
{cin>>n>>c;for(int i=1;i<=n;i++) cin>>a[i],sum+=a[i];dfs(1,0);cout<<bestcw<<endl;for(int i=1;i<=n;i++)cout<<ans[i]<<" ";cout<<endl;
}
signed main()
{solve();return 0;
}01背包问题(回溯+贪心)
剪枝规则:
约束函数:当选取一个物品时,累计的中部不可大于背包容量C
限界函数:根据物品单位重量的价值进行降序排列,越靠近树根位置剪掉分枝越多从而加快搜索;bound(i)定义为当前选取物品价值的和加上剩余物品的价值和,根据贪心的性质,剩余物品不会比贪心选取的物品方案更优,若bound(i)<=此时最优价值,则进行剪枝。
int n,c,cw,cv,bestv;
struct node
{int w,v;double d;
}a[N];
bool cmp(node a,node b)
{return a.d>b.d;
}
int check(int x)
{int v=cv;int tmp=c-cw;while(x<=n&&a[x].w<=tmp){tmp-=a[x].w;v+=a[x].v;x++;}if(x<=n)v+=1.0*tmp*a[x].w;return v;
}
void dfs(int x)
{if(x==n+1){bestv=cv;return;}if(cw+a[x].w<=c){cw+=a[x].w;cv+=a[x].v;dfs(x+1);cw-=a[x].w;cv-=a[x].v;}if(check(x+1)>bestv)dfs(x+1);
}
signed main()
{cin>>c>>n;for(int i=1;i<=n;i++){cin>>a[i].w>>a[i].v;a[i].d=a[i].v*1.0/a[i].w;}sort(a+1,a+n+1,cmp);dfs(1);cout<<bestv<<endl;return 0;
}
/*
50 3
10 60
30 120
20 100
*/n皇后问题
int n,m,a[105][105],p[N],ans;
int check(int x)
{for(int i=1;i<x;i++)if(abs(x-i)==abs(p[x]-p[i])||(p[i]==p[x]))return 0;return 1;
}
void dfs(int x)
{if(x==n+1){ans++;for(int i=1;i<=n;i++)cout<<p[i]<<" ";cout<<endl;return;}for(int i=1;i<=n;i++){p[x]=i;if(check(x))dfs(x+1);}
}
signed main()
{cin>>n;dfs(1);if(ans)cout<<ans<<endl;elsecout<<"No Solution!"<<endl;return 0;
}相关文章:
)
算法复习(四、五、六)
动态规划 动态规划算法的有效性依赖于问题本身所具有的两个重要性质:最优子结构、重叠子问题 关于动态规划算法和备忘录方法的适用条件: 要求: 用分治法和动态规划法分别解决最大子段和问题(第四步求最优解不需要掌握ÿ…...
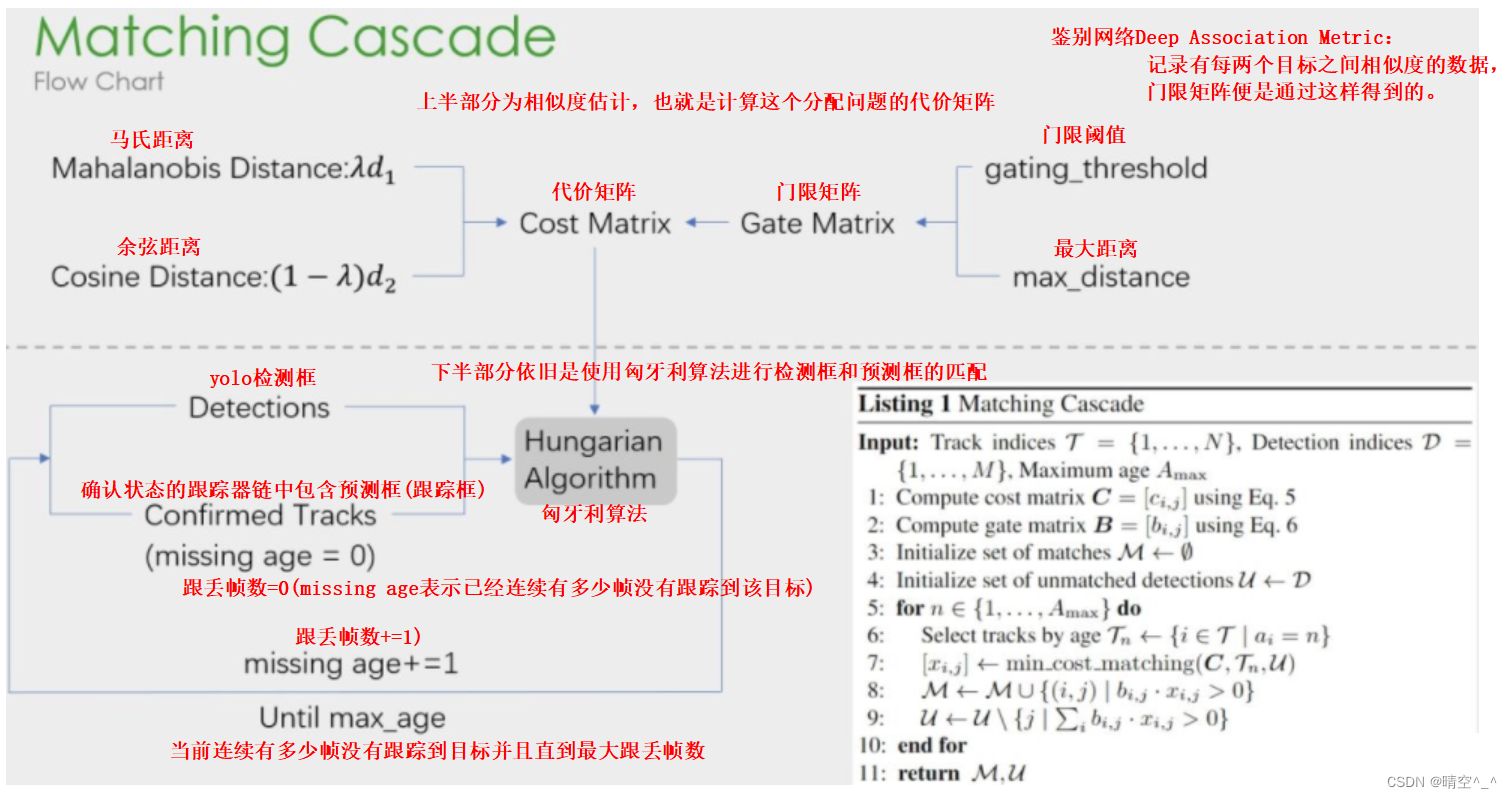
SORT与DeepSORT简介
一、MOT( mutil-object tracking)步骤 在《DEEP LEARNING IN VIDEO MUTIL-OBJECT TEACKING: A SURVEY》这篇基于深度学习多目标跟踪综述中,描绘了MOT问题的四个主要步骤 1.跟定视频原始帧 2.使用目标检测器如Faster-rcnn, YOLO, SSD等进行检测,获取目标…...
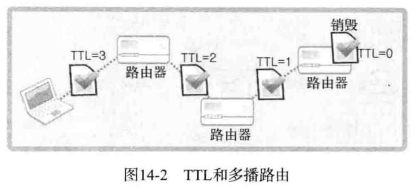
TCP/IP网络编程——多播与广播
完整版文章请参考: TCP/IP网络编程完整版文章 文章目录第 14 章 多播与广播14.1 多播14.1.1 多播的数据传输方式以及流量方面的优点14.1.2 路由(Routing)和 TTL(Time to Live,生存时间),以及加入组的办法14…...

K8S DNS解析过程和延迟问题
一、Linux DNS查询解析原理(对于调用glibc库函数gethostbyname的程序)我们在浏览器访问www.baidu.com这个域名,dns怎么查询到这台主机呢? 1、在浏览器中输入www.baidu.com域名,操作系统会先查找本地DNS解析器缓存&a…...
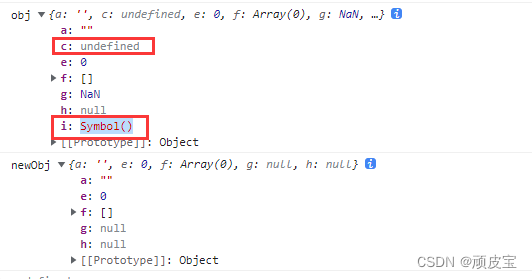
【JavaScript】js实现深拷贝的方法
前言 在js中我们想要实现深拷贝,首先要了解深浅拷贝的区别。 浅拷贝:只是拷贝数据的内存地址,而不是在内存中重新创建一个一模一样的对象(数组) 深拷贝:在内存中开辟一个新的存储空间,完完全全…...

RK3288 GPIO记录
1、引脚对应的GPIO 编号第一种 使用/sys/kernel/debug/gpio查询所有gpio引脚的基数第二种 cat /sys/class/gpio/gpiochip248/label对应的label就是GPIO引脚,例如下图GPIO8对应的基数就是2482、计算编号编号 基数 PIN脚如GPIO8的基数是248, GPIO8_A6的编…...
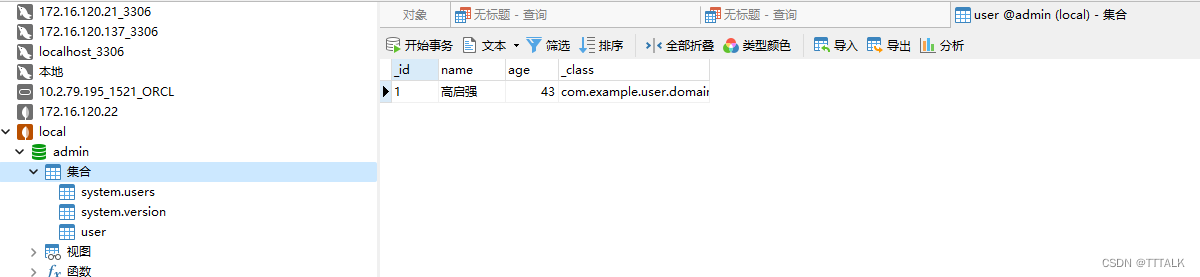
MongoDB介绍及使用教程
文章目录一、MongoDB介绍1. 什么是MongoDB2. 为什么要用MongoDB3. MongoDB的应用场景4. MongoDB基本概念二、MongoDB使用教程1.下载安装(Windows)2.MongoDB Conpass简单使用(选学)3.使用navicat连接MongoDB4.JAVA项目中使用MongoD…...

51单片机开发环境搭建 - VS Code 从编写到烧录
我安装并测试成功的环境: 操作系统:Windows 10 (22H2)单片机:STC89C52RCPython version: 3.7.6 在这之前,给51单片机写程序是用 Keil 5(编写编译)、STC-ISP(烧录),由于…...

python datetime、字符串和时间戳之间的相互转换12小时制和24小时制时间相互转化
文章目录1.字符串转datetime格式2.datetime转字符串3.时间戳转datetime格式4.datetime格式转时间戳5.应用:将12小时制的字符串转换为时间戳1.字符串转datetime格式 把字符串转换为datetime的格式 项目字符串的样子‘%m/%d/%Y %H:%M:%S’2/3/2023 15:30:20‘%m-%d-…...

百度百科词条怎么做?百度百科词条创建攻略分享
只要是想要将自己宣传出去的企业或是个人,都建议创建属于自己的百度百科词条,因为百度百科词条流量大、权重高、排名靠前,创建百度百科词条可以提高企业或是个人的知名度和口碑。 百度百科词条怎么做?每天都有用户在百度上搜索这…...
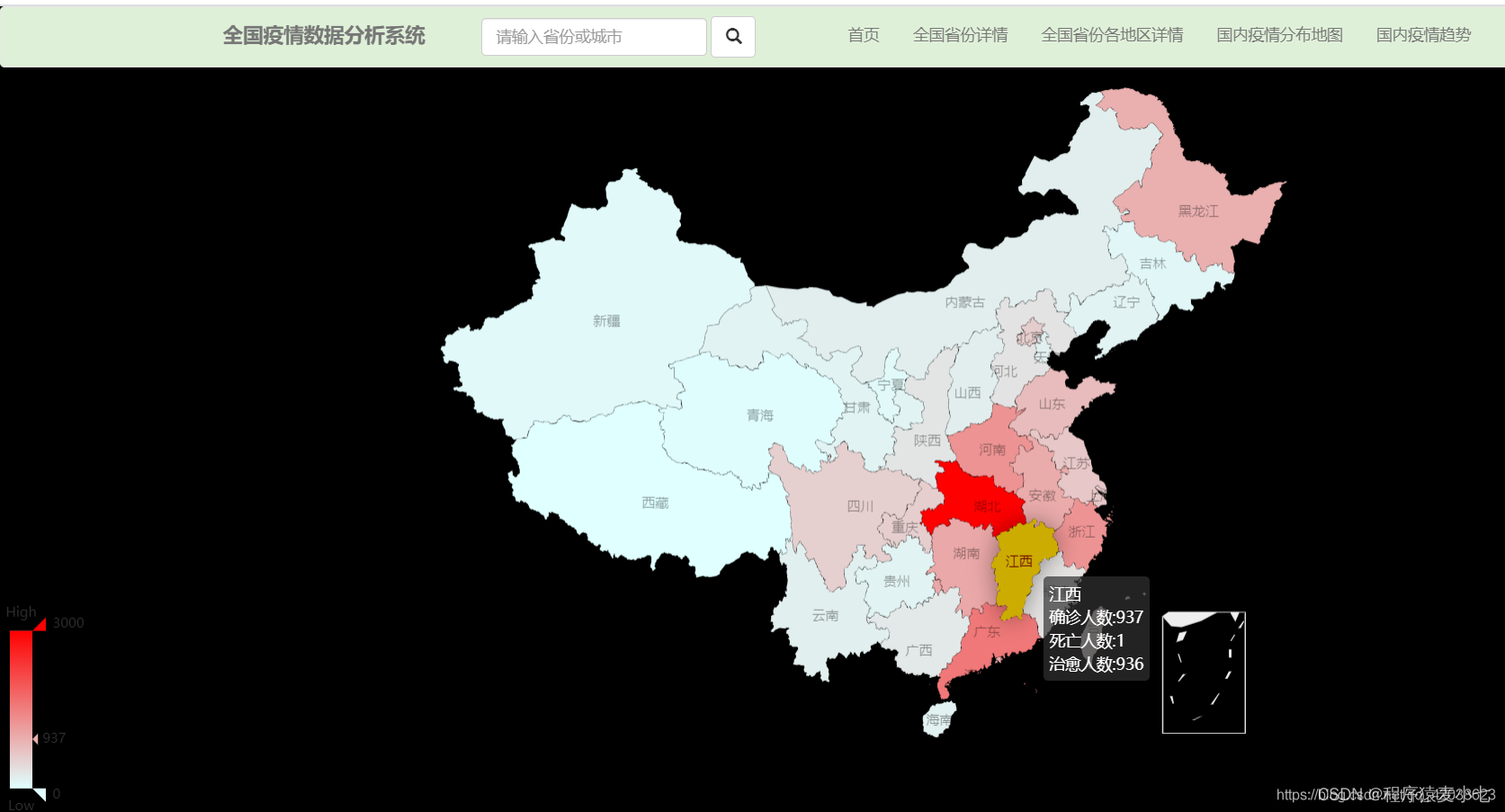
基于Hive的河北新冠确诊人数分析系统的设计与实现
项目描述 临近学期结束,还是毕业设计,你还在做java程序网络编程,期末作业,老师的作业要求觉得大了吗?不知道毕业设计该怎么办?网页功能的数量是否太多?没有合适的类型或系统?等等。这里根据疫情当下,你想解决的问…...

k8s二进制部署
目录 一、环境准备 常见的k8s部署方式 关闭防火墙 关闭selinux 关闭swap 根据规划设置主机名 在master添加hosts 将桥接的IPv4流量传递到iptables的链 时间同步 二、部署etcd集群 1、master节点部署 #查看证书的信息 上传etcd-cert.sh 和etcd.sh 到/opt/k8s/ 目录…...
Windows出现0xc00d36e5错误怎么办?
当我们使用Windows Media Player来播放视频文件时,可能会出现无法播放,并显示0xc00d36e5错误代码。该错误可能是因为Windows Media Player不支持视频格式、注册表项损坏、系统配置问题、第三方应用程序冲突等。下面将开始介绍0xc00d36e5错误的解决方法&a…...
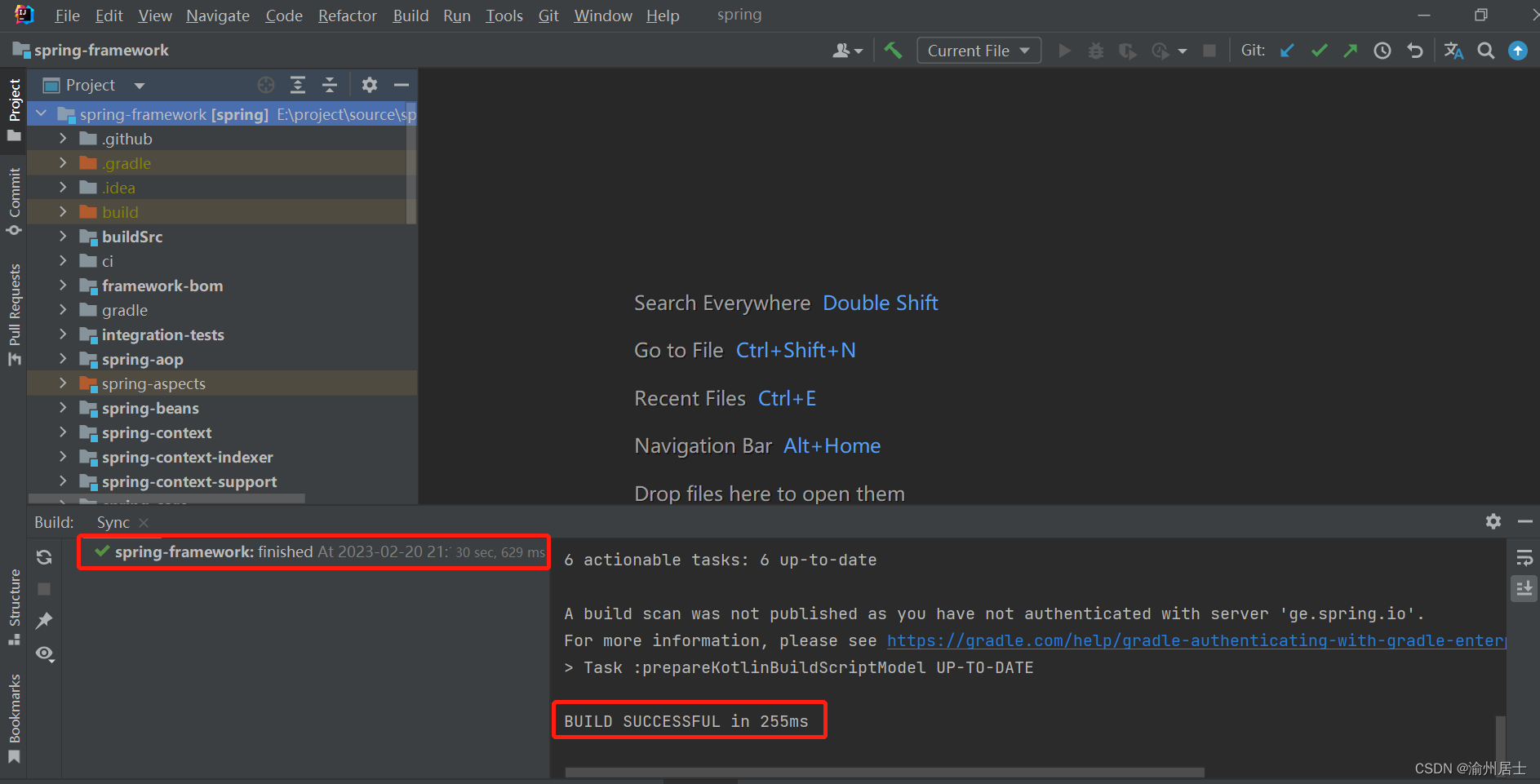
Idea搭建Spring5.3.x源码阅读环境
1. 概述 Spring是一个轻量级Java开源框架,在Java项目开发过程中已经离不开Spring全家桶了,包括Spring、SpringBoot、SpringCloud等,学习好Spring基础源码也有助于更好在项目中使用Spring相关组件,在学习源码前需要搭建好源码学习…...

2.20jdbc
一.数据库编程的必备条件编程语言:java c c Python数据库 Oracle,MySQL,SQL Server数据库驱动包:不同的数据库,对应不同的编程语言提供了不同的数据库驱动包:MySQL提供了Java的驱动包mysqlconnector-java,需要就Java操作MySQL需要该驱动包二.Java的数据库编程JDBC,即…...
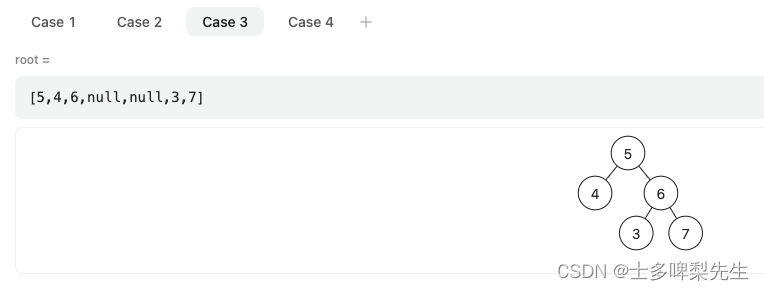
【代码随想录训练营】【Day19休息】【Day20】第六章|二叉树|654.最大二叉树|617.合并二叉树|700.二叉搜索树中的搜索|98.验证二叉搜索树
最大二叉树 题目详细:LeetCode.654 这道题在题目几乎就说明了解题的思路了: 创建一个根节点,其值为 nums 中的最大值;递归地在最大值左边的子数组上构建左子树;递归地在最大值右边的子数组上构建右子树;…...
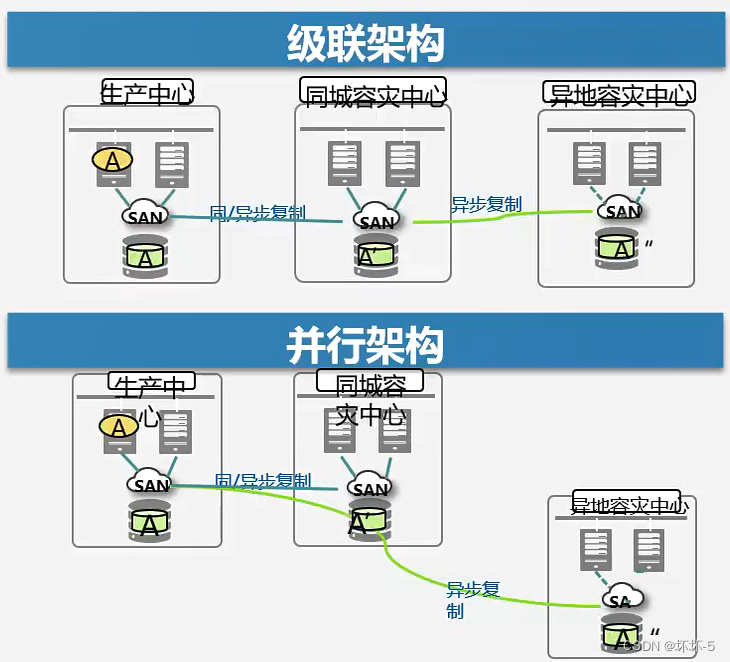
华为云计算之容灾技术
容灾是物理上的容错技术,不是逻辑上的容错同步远程复制:主备距离≤200km,只有在主备设备上都写成功,才会告诉主机写成功,不会丢失数据异步远程复制:主备距离>200km,只要主设备上写成…...

React系列之Redux
1 Redux概述 Redux 是 JavaScript 状态容器,提供可预测化的状态管理。Redux中文文档 Redux 和react没有必然关系,redux可以应用于各种框架,包括jquery,甚至js都可以使用redux,只不过redux和react更加搭配。redux也推…...

最简单得方法解决TCP分包粘包问题
如何用最简单的方法解决TCP传输中的分包粘包问题? 首先需要说明一点,分包粘包等等一系列的问题并不是协议本身存在的问题,而是程序员在写代码的时候,没有搞清楚数据的边界导致的。 看个简单的例子,TCP客户端不断的向服…...
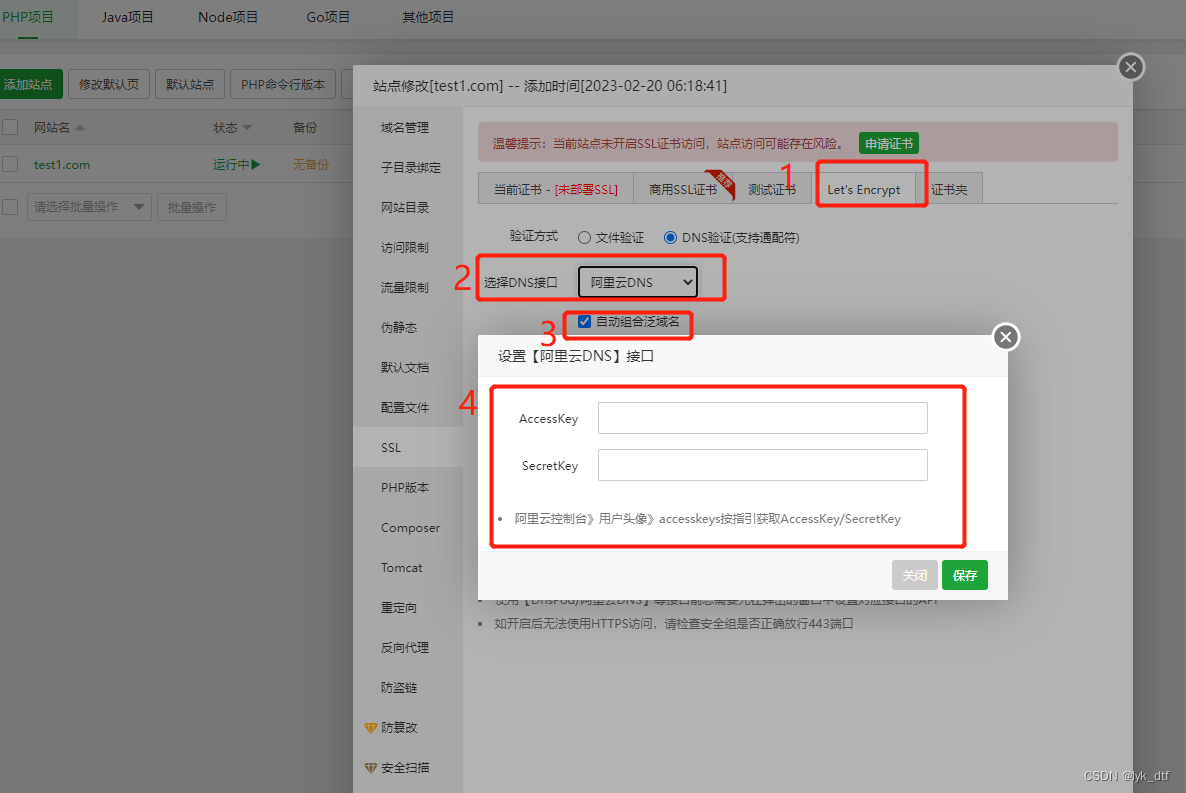
免费使用通配符域名证书
文章目录前言一、手动安装acme.sh操作1、安装acme.sh2、使用dns api自动续签二、宝塔自动操作【推荐】总结前言 之前个人站点一般都是使用阿里云免费单域名证书,虽然好用但是只有一年有效,到期只能手动重新申请,并且每次弄个子域名出来就要重…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
