【代码随想录训练营】【Day19休息】【Day20】第六章|二叉树|654.最大二叉树|617.合并二叉树|700.二叉搜索树中的搜索|98.验证二叉搜索树
最大二叉树
题目详细:LeetCode.654
这道题在题目几乎就说明了解题的思路了:
- 创建一个根节点,其值为 nums 中的最大值;
- 递归地在最大值左边的子数组上构建左子树;
- 递归地在最大值右边的子数组上构建右子树;
- 返回 nums 构建的 最大二叉树 。
显而易见,我可以把构建最大二叉树这个大问题,划分为一个个小问题,当每一棵子树都按照上述思路来构建,那么整体就构成了一棵最大二叉树,小问题思路如下:
- 数组 nums 有三种情况:
- 数组长度为0:说明节点序列为空,返回 null
- 数组长度为1:说明只有一个节点,构建并返回节点
- 数组长度 > 1:找出最大值来构建当前节点
- 找出nums中的最大值,以及最大值的下标
- 按照要求,通过最大值的下标来划分构建左右子树的子数组
- 左子树通过最大值左边的子数组来构建
- 右子树通过最大值右边的子数组来构建
递归从根节点开始到左右子树构建子树,最后返回构建完成的根节点。
Java解法(递归,深度优先遍历):
class Solution {public int findMaxIndex(int[] nums){int res = -1, max = -1;for(int i = 0; i < nums.length; i++){if(max < nums[i]){max = nums[i];res = i;}}return res;}public TreeNode constructMaximumBinaryTree(int[] nums) {if(nums.length == 0)return null;if(nums.length == 1)return new TreeNode(nums[0]);int max_i = this.findMaxIndex(nums);TreeNode root = new TreeNode(nums[max_i]);root.left = this.constructMaximumBinaryTree(Arrays.copyOfRange(nums, 0, max_i));root.right = this.constructMaximumBinaryTree(Arrays.copyOfRange(nums, max_i+1, nums.length));return root;}
}
合并二叉树
题目详细:LeetCode.617
通过合并二叉树的过程,不难发现,在合并过程中会出现这4种情况(这里将要合并的树记作 root1 和 root2,让root2合并到root1):
- root1 != null && root2 != null,那么两个节点的值相加,root1.val += root2.val;
- root1 == null && root2 != null,左节点为空,那么直接将 root2 合并到 root1 中;
- root1 != null && root2 == null,右节点为空,那么无需合并,直接返回左节点
- root1 == null && root2 == null,左右节点都为空,无需合并或二叉树已完成合并
递归从根节点到左右子树开始合并子树,最后返回合并完成的根节点(root1)。
Java解法(递归,深度优先遍历):
class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if(root1 == null){// root1 != null && root2 != nullreturn root2;}else if(root2 == null){// root1 == null && root2 != nullreturn root1;}// root1 != null && root2 == nullroot1.val += root2.val;root1.left = mergeTrees(root1.left, root2.left);root1.right = mergeTrees(root1.right, root2.right);return root1;}
}
二叉搜索树中的搜索
题目详细:LeetCode.700
二叉搜索树的特点可以简要概括为:
- 从根节点开始构建一棵二叉树,使其每一棵子树都满足
- 左节点的值 < 父节点的值
- 右节点的值 > 父节点的值
- 【注意】所以一棵真正的二叉搜索树应满足:
- 左子树上
所有的节点值都 < 父节点的值 - 右子树上
所有的节点值都 > 父节点的值
- 左子树上
- 那么我们则称这棵树为二叉搜索树
那么这道题要求在二叉搜索树中找到目标值对应的子树,利用二叉搜索树的特点和递归来解题就非常清晰易懂了,在搜索过程中会遇到这3种情况:
- 节点为空,则二叉树中不到目标值节点,返回null
- 节点的值 > 目标值,说明目标值只可能在二叉搜索树的右子树出现,递归搜索右子树
- 节点的值 < 目标值,说明目标值只可能在二叉搜索树的左子树出现,递归搜索左子树
- 节点的值 = 目标值,说明当前节点就是我们要找的子树的根节点,返回该节点
Java解法(递归,深度优先遍历):
class Solution {public TreeNode searchBST(TreeNode root, int val) {if(null == root) return null;if(val < root.val){return searchBST(root.left, val);}else if(val > root.val){return searchBST(root.right, val);}// val == root.valreturn root;}
}
验证二叉搜索树
题目详细:LeetCode.98
Java(错误的解法,陷进了一个大坑):
class Solution {public boolean isValidBST(TreeNode root) {return this.dfs(root.left, root.val, true) && this.dfs(root.right, root.val, false);}public boolean dfs(TreeNode root, int father_val, boolean is_left){if(root == null) return true;boolean flag = false;if(is_left){flag = root.val < father_val}else{flag = root.val > father_val}return flag && this.dfs(root.left, root.val, true) && this.dfs(root.right, root.val, false);}
}
一开始我发现这道题很简单,不就是根据二叉搜索树的特点来验证一棵二叉树是不是搜索树么,然后就得出结论:
- 递归验证每一个树的节点是否满足二叉搜索树的特点
- 二叉搜索树的特点在上一题有讲述,这里就不做赘述了
- 如果每一个节点都满足,那么则视作整体满足,返回 true
接着写完我就非常自信地提交了答案!很好,错误的测试例子出现了:

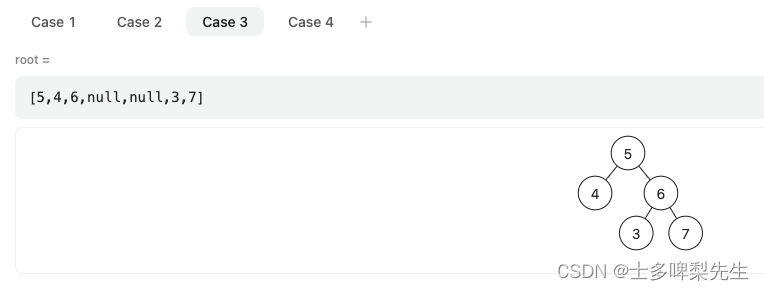
验证了一下算法,发现到达节点值为3的节点时,应该返回 false,因为假如构建一棵二叉搜索树的话,节点3应该是节点4的左节点才对。
所以:
- 不能单纯地对每一个节点判断其是否满足左节点 < 父节点,右节点 > 父节点就完事了。
- 一棵真正的二叉搜索树还需要满足的条件是
左子树所有节点 < 父节点,右子树所有节点 > 父节点。
从二叉搜索树的特点,还可以发现其中序遍历序列,是一个递增序列,那么解题方法忽如一夜春风来,千树万树梨花开呀:
- 解法一:
- 我们可以直接对该二叉树进行中序遍历,获取该树的中序遍历序列;
- 判断该遍历序列是否是递增的,如果是递增序列,则说明该树是二叉搜索树,否则不是。
Java解法(中序遍历,验证二叉搜索树的中序遍历序列是否是递增序列):
class Solution {List<Integer> inorder_list = new ArrayList<>();public void dfs(TreeNode root){if(root == null) return;dfs(root.left);inorder_list.add(root.val);dfs(root.right);}public boolean isValidBST(TreeNode root) {this.dfs(root);int pre = Integer.MIN_VALUE;for(int i: this.inorder_list){if(pre > i) return false;pre = i;}return true;}
}
- 解法二:
- 从解法一可知,我们可以通过验证中序遍历序列是否递增,进而判断该树是否为二叉搜索树
- 那么我们也可以模拟这一思想,改用迭代的算法能够一边遍历节点,一边处理节点
- 一边迭代遍历二叉树,一边比较与前一个遍历的值,来判断遍历序列是否有序,进而判断该树是否为二叉树
Java解法(中序遍历,模拟,迭代,一边遍历一边比较):
class Solution {public boolean inorder(TreeNode root){Stack<TreeNode> stack = new Stack<>();if(null != root) stack.push(root);TreeNode pre = null;while(!stack.isEmpty()){TreeNode node = stack.pop();if(null != node){// 以右根左的顺序进栈,出栈顺序为左根右if(null != node.right) stack.push(node.right);stack.push(node);stack.push(null);if(null != node.left) stack.push(node.left);}else{node = stack.pop();if(null != pre && node.val <= pre.val) return false;pre = node;}}return true;}public boolean isValidBST(TreeNode root) {return this.inorder(root);}
}
天下事有难易乎?为之,则难者亦易矣;不为,则易者亦难矣。人之为学有难易乎?学之,则难者亦易矣;不学,则易者亦难矣。
天下的事情有困难和容易的区别吗?只要肯做,那么困难的事情也变得容易了;如果不做,那么容易的事情也变得困难了。人们做学问有困难和容易的区别吗?只要肯学,那么困难的学问也变得容易了;如果不学,那么容易的学问也变得困难了。
这首诗出自清代彭端淑的《为学一首示子侄》,最近我一直在努力学习,但又一直感觉自己为面试的准备工作很不充分,不敢大胆投简历,也不敢去面试,看完这首诗之后,恍然大悟:
“世上无难事,只怕有心人。”,亦是同样的道理,困难是可以克服的,慢慢来吧。
相关文章:

【代码随想录训练营】【Day19休息】【Day20】第六章|二叉树|654.最大二叉树|617.合并二叉树|700.二叉搜索树中的搜索|98.验证二叉搜索树
最大二叉树 题目详细:LeetCode.654 这道题在题目几乎就说明了解题的思路了: 创建一个根节点,其值为 nums 中的最大值;递归地在最大值左边的子数组上构建左子树;递归地在最大值右边的子数组上构建右子树;…...
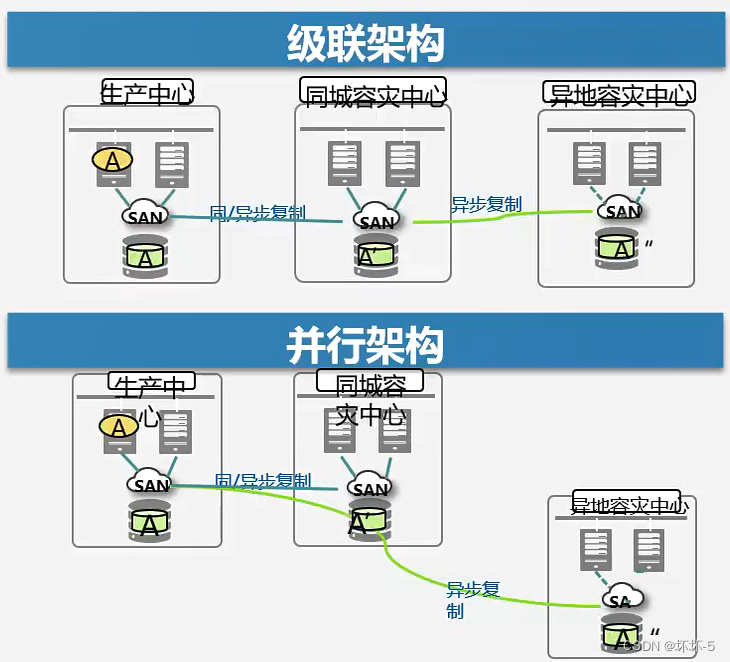
华为云计算之容灾技术
容灾是物理上的容错技术,不是逻辑上的容错同步远程复制:主备距离≤200km,只有在主备设备上都写成功,才会告诉主机写成功,不会丢失数据异步远程复制:主备距离>200km,只要主设备上写成…...

React系列之Redux
1 Redux概述 Redux 是 JavaScript 状态容器,提供可预测化的状态管理。Redux中文文档 Redux 和react没有必然关系,redux可以应用于各种框架,包括jquery,甚至js都可以使用redux,只不过redux和react更加搭配。redux也推…...

最简单得方法解决TCP分包粘包问题
如何用最简单的方法解决TCP传输中的分包粘包问题? 首先需要说明一点,分包粘包等等一系列的问题并不是协议本身存在的问题,而是程序员在写代码的时候,没有搞清楚数据的边界导致的。 看个简单的例子,TCP客户端不断的向服…...
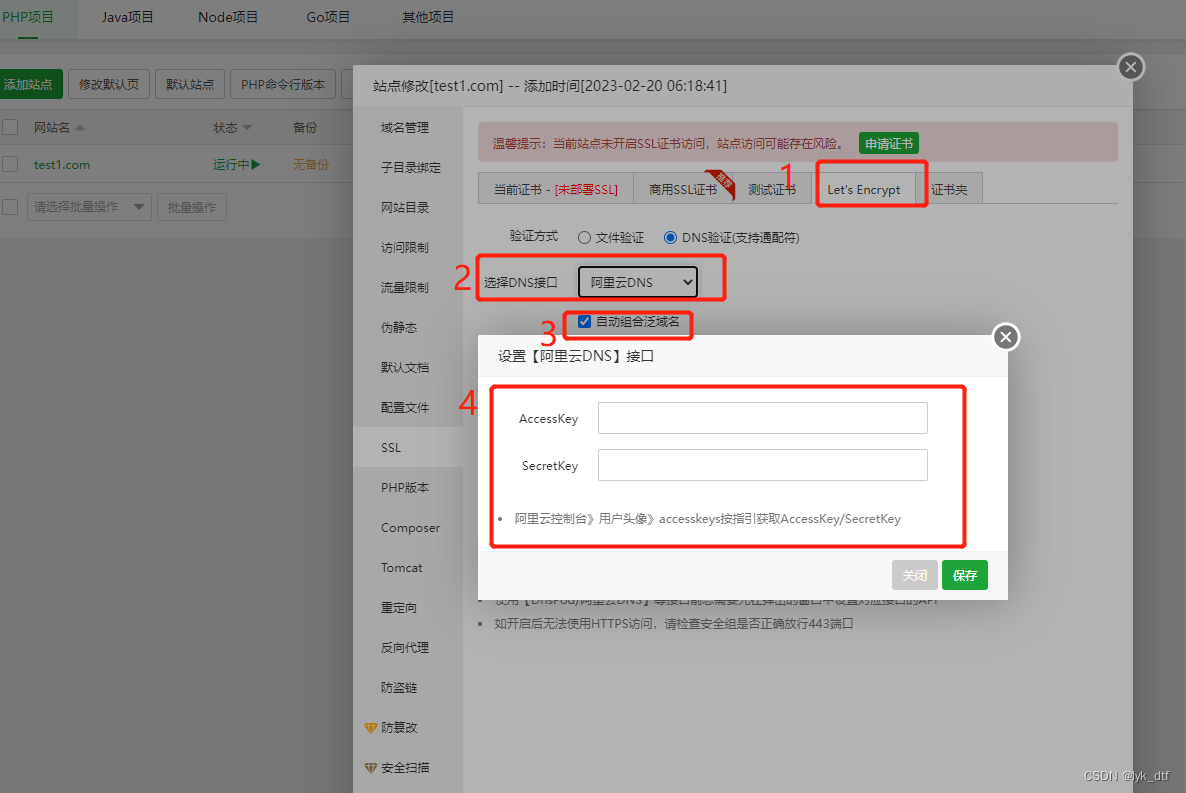
免费使用通配符域名证书
文章目录前言一、手动安装acme.sh操作1、安装acme.sh2、使用dns api自动续签二、宝塔自动操作【推荐】总结前言 之前个人站点一般都是使用阿里云免费单域名证书,虽然好用但是只有一年有效,到期只能手动重新申请,并且每次弄个子域名出来就要重…...

0基础成功转行Python自动化测试工程师,年薪30W+,经验总结都在这(建议收藏)
两年前的决定我觉得还是非常正确的,就是自学了python,然后学习了自动化测试、性能测试、框架、持续集成,同时也把前面的软件测试基础知识全部补全了。目前的收入还比较满意,月入2W(仅代表个人收入),13薪&am…...

MyBaits
MyBaitsMyBaits的jar包介绍MyBaits的入门案例创建实体java日志处理框架常用的日志处理框架Log4j的日志级别Mybatis配置的完善Mybatis的日志管理使用别名alias方式一方式二SqlSession对象下的常用API查询操作Mapper动态代理Mapper 动态代理规范查询所有用户根据用户ID查询用户Ma…...
kubeadm的部署、Dashboard UI以及连接私有仓库
目录 一、kubeadm 部署 K8S 集群架构 1、环境准备 2、所有节点安装docker 3、所有节点安装kubeadm,kubelet和kubectl 3、部署K8S集群 二、dashboard 部署 1、 安装dashboard 2、使用火狐或者360浏览器访问 三 、安装Harbor私有仓库 四、 内核参数优化方案 …...

刷题记录:牛客NC20325[SDOI2009]HH的项链
传送门:牛客 题目描述: HH有一串由各种漂亮的贝壳组成的项链。 HH相信不同的贝壳会带来好运,所以每次散步完后,他都会随意取出一 段贝壳,思考它们所表达的含义。 HH不断地收集新的贝壳,因此他的项链变得越来越长。 有一天&#…...

【REACT-路由v6】
REACT-路由v61. App.js2. 搭建路由2.1 普通写法2.2 使用useRoutes构建路由2.3 重定向封装2.4 嵌套路由中的组件Outlet3. 导航跳转3.2 声明式导航(NavLink标签)3.2 编程式导航跳转(useNavigate)3.2.1 获取参数3.2.1.1 useSearchPar…...
【离散数学】3. 代数系统
1.数理逻辑 2. 集合论 3. 代数系统 4. 图论 代数系统:把一些形式上很不相同的代数系统,用统一的方法描述、研究、推理,从而得到反映出他们共性的一些结论,在将结论运用到具体的代数系统中 系统:运算研究对象 运算&…...

深度学习常用的优化器整理
常见优化器整理 一、SGD(随机梯度下降) 公式: 经典的mini-batch SGD使用的很多,效果也比较不错,但是存在一部分问题 选择恰当的初始学习率很困难学习率调整策略受限于预先制定的调整规则相同的学习率被应用于各个参数…...

Java 内部类
文章目录1、初识内部类2、非静态内部类(实例内部类)3、静态内部类(重点)4、内部类的使用5、局部内部类6、匿名内部类1、初识内部类 如果一个事物的内部包含另一个事物,那么这是一个类的内部包含另一个类。 例如&…...
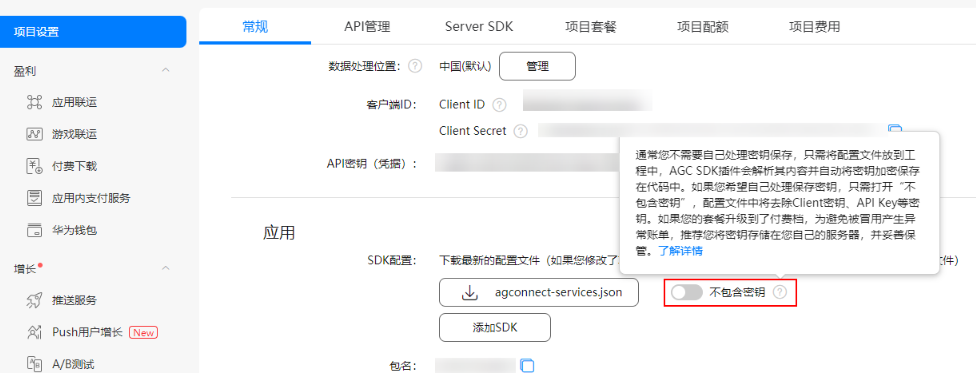
【FAQ】集成分析服务的常见问题及解决方案
常见问题一:如何验证Analytics是否上报/接入成功?以及关键日志含义是什么? 在初始化Analytics SDK前添加SDK日志开关如下: HiAnalyticsTools.enableLog (); 2.初始化SDK代码如下: HiAnalyticsInstance instance Hi…...

11.注意力机制
11.注意力机制 目录 注意力提示 查询、键和值 注意力的可视化 注意力汇聚:Nadaraya-Watson 核回归 生成数据集 非参注意力池化层 Nadaraya-Watson核回归 参数化的注意力机制 批量矩阵乘法 定义模型 训练 注意力评分函数 掩蔽softmax操作 加性注意力 缩…...

45岁当打之年再创业,剑指中国版ChatGPT,这位美团联合创始人能否圆梦?
文 BFT机器人 “即便只有一个人,我也要出发。” 这是45岁的前美团联合创始人王慧文再次冲上创业沙场的“征战”宣言,这一次他的梦想是“组队拥抱新时代,打造中国OpenAI”。 01 当打之年, AI新梦再起航 “我的人工智能宣言&…...
——链式存储结构)
数据结构——第二章 线性表(2)——链式存储结构
链式存储结构1 线性表的链式存储结构1.1不带头结点的单向链表1.2 带头结点的单向链表2 单向链表的基本操作实现2.1 单向链表的初始化操作2.2 单向链表的插入操作2.3. 单链表的删除操作2.4.单向链表的更新操作2.5.单向链表的求长度操作2.6.单向链表的定位操作2.7.单向链表的遍历…...
)
【更新】囚生CYの备忘录(20230216~)
序言 阳历生日。今年因为年过得早的缘故,很多事情都相对提前了(比如情人节)。往年过生日的时候基本都还在家,所以一家子出去吃个饭也就罢了。今年承蒙凯爹厚爱,正好也有小半年没聚,他前天也刚正式拿到offe…...
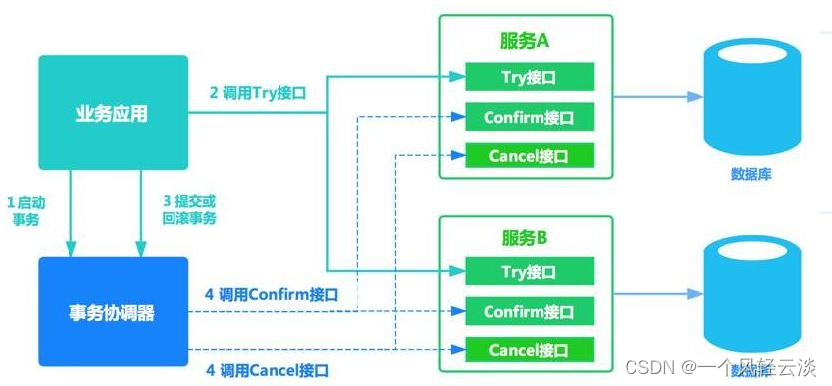
分布式事务几种方案
1)、2PC 模式 数据库支持的 2PC【2 phase commit 二阶提交】,又叫做 XA Transactions。 MySQL 从 5.5 版本开始支持,SQL Server 2005 开始支持,Oracle 7 开始支持。 其中,XA 是一个两阶段提交协议,该协议…...
Eclipse各版本安装Tomcat插件全攻略
Eclipse Tomcat 插件的作用 Eclipse Tomcat 插件可以将Tomcat 集成到Eclipse中,插件安装之后在Eclipse中可以看到类似下面的几个图标: Eclipse Tomcat 插件的主要作用有: 在Eclipse 中可以直接启动,关闭和重启本机的Tomcat可以…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
