【离散数学】3. 代数系统
1.数理逻辑
2. 集合论
3. 代数系统
4. 图论
代数系统:把一些形式上很不相同的代数系统,用统一的方法描述、研究、推理,从而得到反映出他们共性的一些结论,在将结论运用到具体的代数系统中
系统:运算+研究对象
- 运算:具有的共同性质的不同演算抽取成一个运算,根据性质的不同取名群、环域等。
- 研究对象:可以运算的抽象对象
如:集合上的并满足结合律,实数上的加法也满足结合律,用一个符号代表具有结合律的运算,而研究对象变为代表实数或者集合等对象的抽象事物
所以代数系统定义为:非空集合和定义在集合上的封闭运算构成的系统
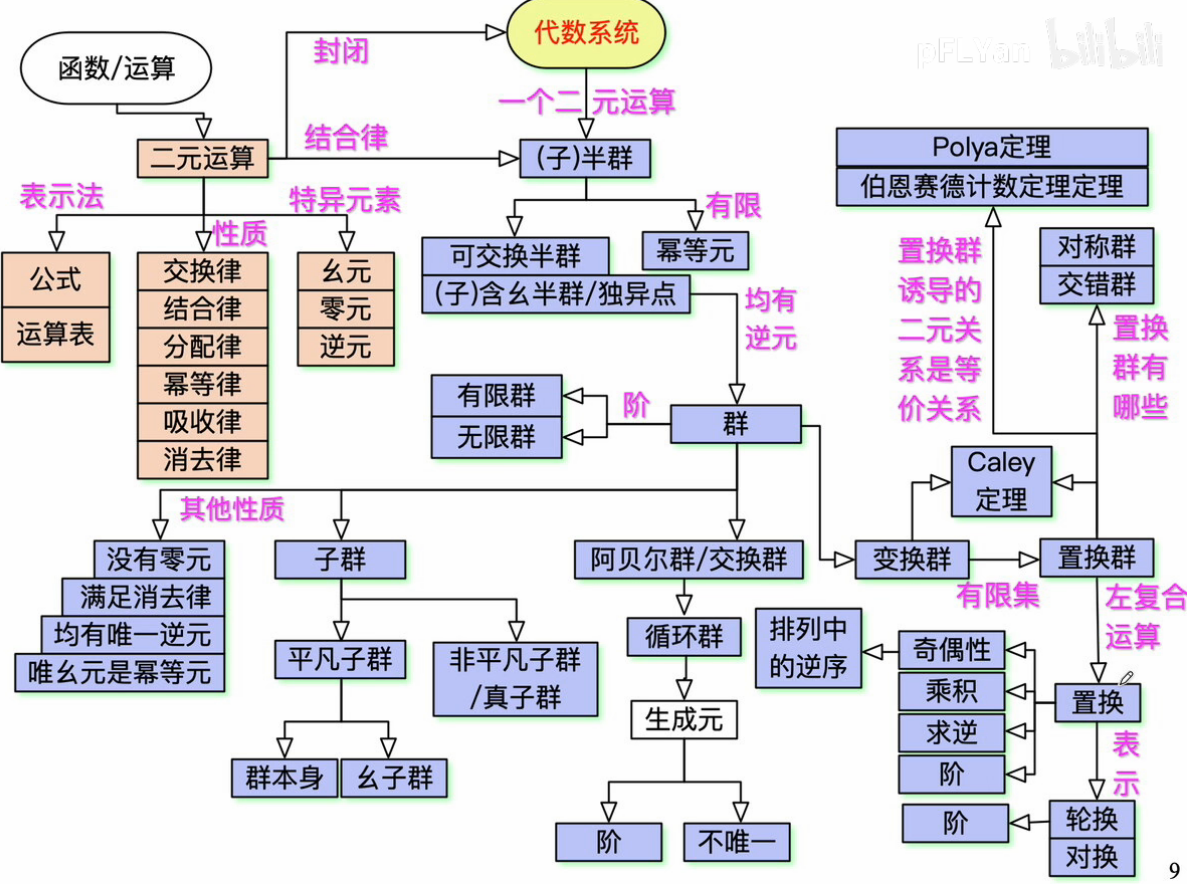
5. 代数系统
5.0 代数学
代数学:研究数的部分
几何学:研究形的部分
分析学:沟通数与性且设计极限运算的部分
代数:用字母代替具体的数值
发展历程
-
算数
-
初等代数
-
代数式的运算、方程
从简单的一元一次方程开始
讨论二元和三元的一次方程
研究二元以上及可以转换为二元的方程组
-
数与方程理论
- 无理数与有理数的界定
- 运算符号的创立与无理方程的解法
- 虚数理论
-
高等代数
-
线性代数:讨论任意多个未知数的一元方程组(线性方程组)
费马与笛卡尔引入笛卡尔坐标系,统一了代数与集合,线性代数才出现
仅涉及线性运算(加法和数乘)的代数学分支,以矩阵为研究工具,以向量空间和线性映射为研究对象
-
多项式代数:研究更高次的一元方程组
-
-
(19世纪以后)抽象代数
系统:将不同演算共有的性质抽取形成系统,根据抽取的性质取名群、环域等。
如:集合上的并有结合律,实数上的加法也有结合律,用一个符号代表具有结合律的运算,而研究对象变为代表实数或者集合等对象的抽象事物
所以代数系统定义为:抽象的研究对象集合和满足某种性质的运算构成的系统
具体应用:
伽罗瓦用置换群的方法证明一般形式的一元五次方程没有通解,给出了可解性的判别原则
格与布尔代数:用于电子线路设计、电子计算机硬件设计和通信系统设计
半群:形式语言,自动机理论
5.1 运算
5.1.1 运算的概念
二元运算:函数 f:A×A→Af:A\times A\rightarrow Af:A×A→A,则称f为A上的二元代数运算
如:
-
加法与乘法是在 Z+Z^+Z+ 上的二元代数运算,运算结果也是 Z+Z^+Z+ ,所以是封闭的
f(<x,y>)=x+y,x∈Z+,y∈Z+,x+y∈Z+f(<x,y>)=x+y,x\in Z^+,y\in Z^+,x+y\in Z^+f(<x,y>)=x+y,x∈Z+,y∈Z+,x+y∈Z+
-
减法不是 Z+Z^+Z+ 上的二元运算,因为 x−y∉?Z+x-y\notin^{?} Z^+x−y∈/?Z+ ,所以是不封闭的
-
减法在Z上是二元运算,x−y∈Zx-y\in Zx−y∈Z ,是封闭的
5.1.2 运算的性质
二元运算 A×A→AA\times A\rightarrow AA×A→A 上的性质,以*为运算符
交换律
∀x,y∈A,有x∗y=y∗x,称∗满足交换律\forall x,y\in A,有x*y=y*x,称 *满足交换律 ∀x,y∈A,有x∗y=y∗x,称∗满足交换律
运算表关于主对角线对称
结合律
∀x,y,z∈A,有(x∗y)∗z=x∗(y∗z),称∗满足结合律\begin{aligned} \forall x,y,z\in A,有(x*y)*z=x*(y*z),称*满足结合律 \end{aligned} ∀x,y,z∈A,有(x∗y)∗z=x∗(y∗z),称∗满足结合律
分配律
∀x,y,z∈A,有{x∗(y⋅z)=x∗y⋅x∗z(y⋅z)∗x=y∗x⋅z∗x,则称∗满足分配律\forall x,y,z\in A,有\begin{cases} x*(y·z)=x*y·x*z\\ (y·z)*x=y*x·z*x \end{cases} ,则称*满足分配律 ∀x,y,z∈A,有{x∗(y⋅z)=x∗y⋅x∗z(y⋅z)∗x=y∗x⋅z∗x,则称∗满足分配律
幂等律
∀x∈A,有x∗x=x,则称∗满足幂等律若∃a∈A,且a∗a=a,则称a是∗的幂等元\begin{aligned} &\forall x\in A,有x*x=x,则称*满足幂等律\\ &若\exists a\in A,且a*a=a,则称a是*的幂等元 \end{aligned} ∀x∈A,有x∗x=x,则称∗满足幂等律若∃a∈A,且a∗a=a,则称a是∗的幂等元
主对角线元素排列与表头顺序一直
吸收律
∀x,y∈A,有{x∗(x⋅y)=xx⋅(x∗y)=x,则称∗和⋅满足吸收律\forall x,y \in A,有 \begin{cases} x*(x·y)=x\\ x·(x*y)=x \end{cases}, 则称*和·满足吸收律 ∀x,y∈A,有{x∗(x⋅y)=xx⋅(x∗y)=x,则称∗和⋅满足吸收律
消去律
若满足两个关系:{x∗y=x∗z(x≠0),则y=zy∗x=z∗x(x≠0),则y=z,∗满足消去律若满足两个关系: \begin{cases} x*y=x*z(x\neq 0),则y=z\\ y*x=z*x(x\neq 0),则y=z \end{cases} ,*满足消去律 若满足两个关系:{x∗y=x∗z(x=0),则y=zy∗x=z∗x(x=0),则y=z,∗满足消去律
Z上的加法、乘法满足消去律
幂集 ρ(A)\rho(A)ρ(A) 上的 U 不满足消去律
- A∪B=A∪C⇏B=CA\cup B=A\cup C \nRightarrow B=CA∪B=A∪C⇏B=C
5.1.3 表示方法
- 公式
- 运算表
5.2 代数系统
5.2.1 基本概念
代数系统:非空集合A和A上的k个封闭的运算 f1,f2,...,fkf_1,f_2,...,f_kf1,f2,...,fk 组成的系统,称为一个代数系统,记作 <A,f1,f2,...,fk><A,f_1,f_2,...,f_k><A,f1,f2,...,fk>
如: <R,+>,<R,∗>,<ρ(A),∪,∩><R,+>,<R,*>,<\rho(A),\cup,\cap><R,+>,<R,∗>,<ρ(A),∪,∩>
子代数系统:设 <A,∗1,∗2,...,∗k><A,*_1,*_2,...,*_k><A,∗1,∗2,...,∗k> 是代数系统,若 B⊆A,B≠∅B\subseteq A,B\neq ∅B⊆A,B=∅ ,且运算 ∗1,∗2,...,∗k*_1,*_2,...,*_k∗1,∗2,...,∗k 对B是封闭的,则 <B,∗1,∗2,...,∗k><B,*_1,*_2,...,*_k><B,∗1,∗2,...,∗k> 也是代数系统,称为 <A,∗1,∗2,...,∗k><A,*_1,*_2,...,*_k><A,∗1,∗2,...,∗k> 的子代数系统
若 B⊂AB\subset AB⊂A,则称 <B,∗1,∗2,...,∗k><B,*_1,*_2,...,*_k><B,∗1,∗2,...,∗k> 为真子代数系统
如:
对<R,−>:<Z,−>是<R,−>的真子代数系统<N,−>不是<R,−>的真子代数系统对<R,->: \begin{aligned} &<Z,->是<R,->的真子代数系统\\ &<N,->不是<R,->的真子代数系统 \end{aligned} 对<R,−>:<Z,−>是<R,−>的真子代数系统<N,−>不是<R,−>的真子代数系统
5.2.2 特殊元
幺元零元
代数系统的幺元,零元 ,若存在必唯一
左幺元:设*是S上的二元运算,1l1_l1l 是S中的元素,如果对S中的每一元素x,有1l∗x=x1_l*x=x1l∗x=x,则称 1l1_l1l 是对运算 * 的左幺元
左零元:如果对于S中的每个元素x,有 0l∗x=0l0_l*x=0_l0l∗x=0l ,则称 0l0_l0l 对运算 * 是左零元
设 * 是S上的二元运算,1是S中的元素,对于S中的每个元素,满足 1∗x=x∗1=x1*x=x*1=x1∗x=x∗1=x ,则1为对运算 * 的幺元。
如果对于S中的每一元素x,有 0∗x=x∗0=00*x=x*0=00∗x=x∗0=0 ,则称0对运算 * 是零元
- 在运算表中
- 幺元:所在的行与列的元素排列都与表头一致
- 零元:元素的行与列都有钙元素自身构成
逆元
某个元素的逆元
设 * 是S上的二元运算,1是对运算 * 的幺元。如果 x*y =1,那么关于运算 * ,x是y的左逆元,y是x的右逆元
如果 x*y=1和y*x=1都成立,则关于运算 *,x是y的逆元
x的逆元记作 x−1x^{-1}x−1 ,存在逆元的元素称为可逆的

5.3 含一个运算的代数系统
5.3.1 半群
设 V=<S,∗>V=<S,*>V=<S,∗> 是代数系统,* 为一个二元运算符
- 若 * 是可结合的,则称V是半群
如:乘法,加法,关系的合成,<ρ(A),∪>,<ρ(A),∩><\rho(A),\cup>,<\rho(A),\cap><ρ(A),∪>,<ρ(A),∩> 都是半群
幂等元:∃a∈S,使得a2=a\exists a\in S,使得 a^2=a∃a∈S,使得a2=a 成立,则称a是幂等元素
-
定理:有限半群必有幂等元
连续幂等后根据封闭性,结果仍在集合中,所以一定存在幂等元
子半群
在非空子集上的运算是封闭的半群
独异点(含幺半群)
含幺半群=半群+幺元
半群V中 * 运算符含有幺元,则称V是含幺半群(独异点),记作 <S,∗,1><S,*,1><S,∗,1>
如:矩阵乘法
证明独异点
在R中定义二元运算 * ,∀a,b∈R,a∗b=a+b+ab\forall a,b \in R,a*b=a+b+ab∀a,b∈R,a∗b=a+b+ab ,求证 <R,∗><R,*><R,∗> 构成独异点
1.∀a,b∈R,a∗b=a+b+ab∈R,所以∗是封闭的即<R,∗>是一个代数系统2.(a∗b)∗c=(a∗b)+c+(a∗b)c=(a+b+ab)+c+(a+b+ab)c=a+b+c+ab+ac+bc+abcc∗(a∗b)=c+(a∗b)+c(a∗b)=c+(a+b+ab)+c(a+b+ab)=a+b+c+ab+ac+bc+abc所以∗是可结合的,故<R,∗>是半群3.对0∈R,∀x∈R,有0∗x=x=x∗0=x,所以0为幺元综上,<R,∗>是独异点\begin{aligned} 1.\quad &\forall a,b \in R,a*b=a+b+ab\in R,所以*是封闭的\\&即<R,*>是一个代数系统\\ 2.\quad &(a*b)*c=(a*b)+c+(a*b)c=(a+b+ab)+c+(a+b+ab)c\\&=a+b+c+ab+ac+bc+abc\\ &c*(a*b)=c+(a*b)+c(a*b)=c+(a+b+ab)+c(a+b+ab)\\&=a+b+c+ab+ac+bc+abc\\ &所以 *是可结合的,故<R,*>是半群\\ 3.\quad &对0\in R,\forall x\in R,有0*x=x=x*0=x,所以0为幺元\\ &综上,<R,*>是独异点 \end{aligned} 1.2.3.∀a,b∈R,a∗b=a+b+ab∈R,所以∗是封闭的即<R,∗>是一个代数系统(a∗b)∗c=(a∗b)+c+(a∗b)c=(a+b+ab)+c+(a+b+ab)c=a+b+c+ab+ac+bc+abcc∗(a∗b)=c+(a∗b)+c(a∗b)=c+(a+b+ab)+c(a+b+ab)=a+b+c+ab+ac+bc+abc所以∗是可结合的,故<R,∗>是半群对0∈R,∀x∈R,有0∗x=x=x∗0=x,所以0为幺元综上,<R,∗>是独异点
定理
- x,y都有逆元,则 x*y 有逆元,且 (x∗y)−1=x−1∗y−1(x*y)^{-1}=x^{-1}*y^{-1}(x∗y)−1=x−1∗y−1
可交换半群=半群+满足交换律
若半群 V=<S,∗>V=<S,*>V=<S,∗> 的运算符 * 是可交换的,V是可交换半群
定理
- 在可交换半群 <S,∗><S,*><S,∗> 中,有 (a∗b)n=an∗bn(a*b)^n=a^n*b^n(a∗b)n=an∗bn ,其中n是正整数, a,b∈Sa,b\in Sa,b∈S
独异点 <S,∗,1><S,*,1><S,∗,1> 中的 * 是可交换的,称V是可交换独异点
循环半群=半群+生成元
5.3.2 群
群=含幺半群+每个元素有逆元
设 V=<S,∗>V=<S,*>V=<S,∗> 是代数系统,* 是二元运算
若 * 是可结合的,存在幺元 ∃1∈S\exists 1 \in S∃1∈S ,且 ∀x∈S,有x−1∈S\forall x\in S,有x^{-1}\in S∀x∈S,有x−1∈S ,称V为群
如:
<N,+>满足结合律,所以是半群。幺元是0,所以是含幺半群。但是<N,+>不是群,每个元素的逆不在N中\begin{aligned} &<N,+>满足结合律,所以是半群。幺元是0,所以是含幺半群。但是\\ &<N,+>不是群,每个元素的逆不在N中 \end{aligned} <N,+>满足结合律,所以是半群。幺元是0,所以是含幺半群。但是<N,+>不是群,每个元素的逆不在N中
证明群的过程
设Z为整数集合,在Z上定义二元运算*,∀x,y∈Z\forall x,y\in Z∀x,y∈Z,x*y=x+y-2,为 <Z,∗><Z,*><Z,∗> 是否为群
1.∀x,y∈Z,x∗y=x+y−2∈Z,所以∗是封闭的,即<Z,∗>是代数系统2.∀x,y,z∈Z(x∗y)∗z=(x+y−2)+z−2=x+y+z−4x∗(y∗z)=x+(y+z−2)−2=x+y+z−4即∗是可结合的,所以<Z,∗>是半群3.设p是幺元,p∗x=p=p+x−2=x⇒p=2故半群<R,∗>是独异点,幺元为24.x∗x−1=2⟺x+x−1=4⇒x−1=4−x∈Z故<R,∗>是群\begin{aligned} 1.\quad &\forall x,y\in Z,x*y=x+y-2\in Z,所以*是封闭的,即<Z,*>是代数系统\\ 2.\quad &\forall x,y,z\in Z \\ &(x*y)*z=(x+y-2)+z-2=x+y+z-4\\ &x*(y*z)=x+(y+z-2)-2=x+y+z-4\\ &即*是可结合的,所以<Z,*>是半群\\ 3.\quad &设p是幺元,p*x=p=p+x-2=x\Rightarrow p=2\\ &故半群<R,*>是独异点,幺元为2\\ 4.\quad &x*x^{-1}=2\iff x+x^{-1}=4\Rightarrow x^{-1}=4-x\in Z\\ &故<R,*>是群 \end{aligned} 1.2.3.4.∀x,y∈Z,x∗y=x+y−2∈Z,所以∗是封闭的,即<Z,∗>是代数系统∀x,y,z∈Z(x∗y)∗z=(x+y−2)+z−2=x+y+z−4x∗(y∗z)=x+(y+z−2)−2=x+y+z−4即∗是可结合的,所以<Z,∗>是半群设p是幺元,p∗x=p=p+x−2=x⇒p=2故半群<R,∗>是独异点,幺元为2x∗x−1=2⟺x+x−1=4⇒x−1=4−x∈Z故<R,∗>是群
有限群&无限群
设 <G,∗><G,*><G,∗> 是一个群
-
如果G是有限集,则称 <G,∗><G,*><G,∗> 是有限群,G中的元素个数称为群的阶,记为 ∣G∣\mid G \mid∣G∣
-
G是无限集,则为无限群,群的阶为无限
群的基本性质
二阶以上的群无零元
- 一阶群一定有零元,零元即幺元, <g,∗><{g},*><g,∗> g*g=g,所以g是零元
群中每个元素都存在唯一逆元
群中除幺元外无幂等元
群的运算表中,没有两行或两列是相同的
群满足消去律
满足消去律的有限半群是群
- 没有零元的有限半群是群
子群
设 <G,∗><G,*><G,∗> 为群,H⊆GH\subseteq GH⊆G,且 <H,∗><H,*><H,∗> 为群,则称H为G的子群,记作 H≤GH\le GH≤G
子群判定定理
设 <G,∗><G,*><G,∗> 为群,H是G的非空子集
<H,∗>是<G,∗>的非空子群⟺{封闭:∀a,b∈H,有a∗b∈H逆元:∀a∈H,有a−1∈H⟺∀a,b∈H,有a∗b−1∈HH是G的子集且H是有限集⟺∀a,b∈H,有a∗b∈H\begin{aligned} <H,*>是<G,*>的非空子群 &\iff \begin{cases} 封闭:\forall a,b\in H,有a*b\in H\\ 逆元:\forall a\in H,有a^{-1}\in H \end{cases}\\ &\iff \forall a,b\in H,有a*b^{-1}\in H\\ H是G的子集且H是有限集&\iff \forall a,b\in H,有a*b\in H \end{aligned} <H,∗>是<G,∗>的非空子群H是G的子集且H是有限集⟺{封闭:∀a,b∈H,有a∗b∈H逆元:∀a∈H,有a−1∈H⟺∀a,b∈H,有a∗b−1∈H⟺∀a,b∈H,有a∗b∈H
性质
子群的幺元是群的幺元,∀a∈H\forall a\in H∀a∈H ,其逆元 aH−1a_H^{-1}aH−1 就是a在G中的逆元 a−1a^{-1}a−1
二阶以上的群 <G,∗><G,*><G,∗> 一定存在两个子群,称为G的平凡子群
-
由幺元组成的子群 <1,∗><{1},*><1,∗> 称为G的幺子群,其中 1就是 <G,∗><G,*><G,∗> 的幺元
-
<G,∗><G,*><G,∗> 群本身
-
其余子群称为 非平凡子群/真子群
交换群:满足交换律的群
若群 V=<S,∗>V=<S,*>V=<S,∗> 中的 * 满足交换律,则称V是可交换的群(阿贝尔群)

循环群:有生成元的交换群
群中的每个元素都可用一个元素的方幂表示,则称这个群是循环群
群 V=<G,∗>V=<G,*>V=<G,∗> 中,如果 ∃g∈G\exists g\in G∃g∈G,对于每个元素 a∈Ga\in Ga∈G,都有一个相应的 i∈Ii\in Ii∈I ,能把a表示成幂次 gig^igi 的形式,则称 <G,∗><G,*><G,∗> 是一个循环群。或循环群是由g生成的,g是 <G,∗><G,*><G,∗> 的生成元
循环群的判别
证明:<Z,+><Z,+><Z,+> 是循环群
1.∀a,b∈Z,a+b∈Z,故+是封闭的<G,+>是一个代数系统2.∀a,b,c∈Z,(a+b)+c=a+(b+c)=a+b+c所以<G,+>是半群3.设幺元为p,∀x∈Z,p+x=x,则p=0幺元=04.∀a∈Z,a+a−1=0⇒a−1=−a∈Z所以<G,+>是群5.设g=1,∀n∈Z+,n=1+1+...+1=1n∀n∈Z−,n=(−1)+(−1)+...+(−1)=(−1)n=(1−1)n故1是<G,∗>的生成元,该群为循环群\begin{aligned} &1. \quad \forall a,b\in Z,a+b\in Z,故+是封闭的\\ & \quad <G,+>是一个代数系统\\ &2.\quad \forall a,b,c \in Z,(a+b)+c=a+(b+c)=a+b+c\\ &\quad 所以<G,+>是半群\\ &3.\quad 设幺元为p,\forall x\in Z,p+x=x,则p=0\\ &\quad 幺元=0\\ &4. \quad \forall a\in Z,a+a^{-1}=0\Rightarrow a^{-1}=-a\in Z\\ &\quad 所以<G,+>是群\\ &5. \quad 设g=1,\forall n\in Z_+,n=1+1+...+1=1^{n}\\ &\quad \forall n\in Z_-,n=(-1)+(-1)+...+(-1)=(-1)^n=(1^{-1})^n\\ &故1是<G,*>的生成元,该群为循环群 \end{aligned} 1.∀a,b∈Z,a+b∈Z,故+是封闭的<G,+>是一个代数系统2.∀a,b,c∈Z,(a+b)+c=a+(b+c)=a+b+c所以<G,+>是半群3.设幺元为p,∀x∈Z,p+x=x,则p=0幺元=04.∀a∈Z,a+a−1=0⇒a−1=−a∈Z所以<G,+>是群5.设g=1,∀n∈Z+,n=1+1+...+1=1n∀n∈Z−,n=(−1)+(−1)+...+(−1)=(−1)n=(1−1)n故1是<G,∗>的生成元,该群为循环群
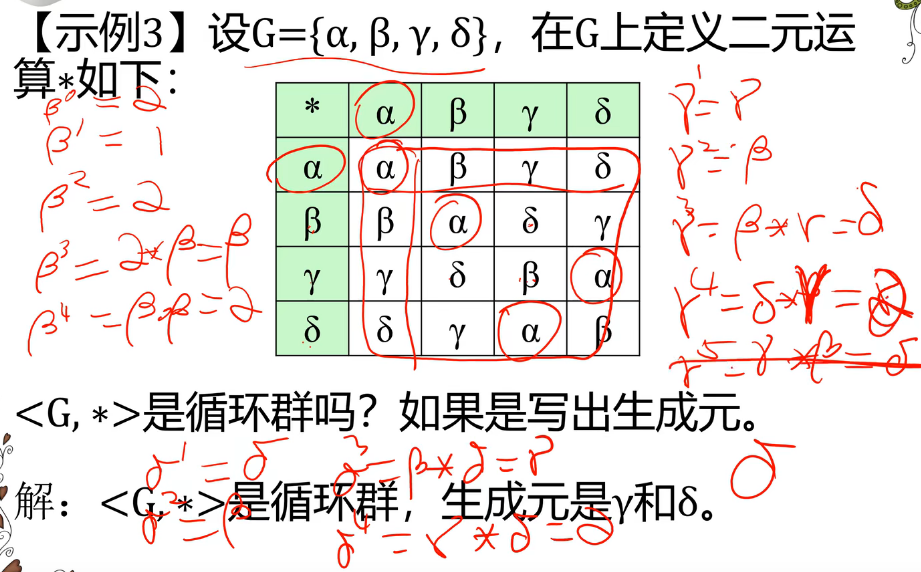
循环群的性质
-
生成元不唯一

-
群的阶:设 <G,∗><G,*><G,∗> 是一个由元素a生成的循环群,且是 有限群,如果G的阶是n,即 ∣G∣=n\mid G \mid=n∣G∣=n ,则 an=1a^n=1an=1 且 G={a,a2,...,an=1}G=\{a,a^2,...,a^n=1\}G={a,a2,...,an=1} ,n是元素 a 的阶(使得 an=1a^n=1an=1 成立的最小正整数)
-
任意的循环群都是交换群

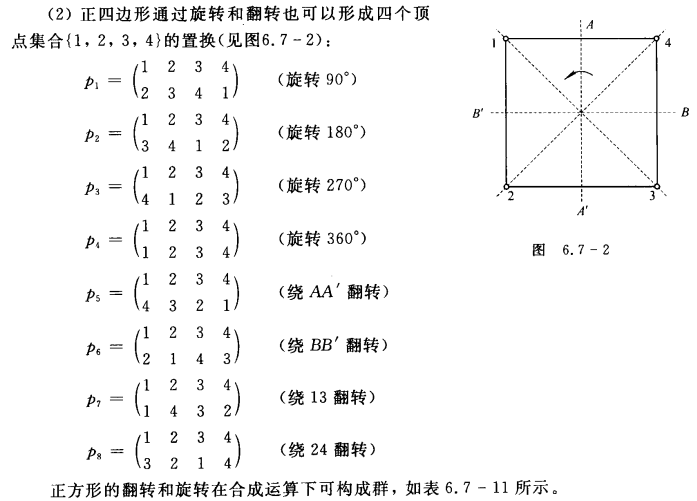
置换群
变换与变换群
变换:在A上的映射/函数
对称群 <SA,◇><S_A,◇><SA,◇>:非空集合A 上的全体 可逆变换(双射函数)的复合运算 构成集合的A的群
- 代数系统——封闭:集合A上的任意两个双射函数复合后仍在集合A中
- 半群——结合律:复合运算具有结合律
- 含幺半群——求幺元:恒等函数,自己到自己的变换
- 群——每个元素逆元都在群中:双射函数的逆元仍在集合中
对称群 <SA,◇><S_A,◇><SA,◇> 的子群称为A的一个变换群
- 运算符号满足结合律,不满足交换律
- 每个群都同构于一个变换群
G是实数集R上 所有变换 fa,b:R→Rf_{a,b}:R\rightarrow Rfa,b:R→R 构成的集合,∀x∈R,fa,b(x)=ax+b\forall x\in R,f_{a,b}(x)=ax+b∀x∈R,fa,b(x)=ax+b , <G,◇><G,◇><G,◇> G是变换群
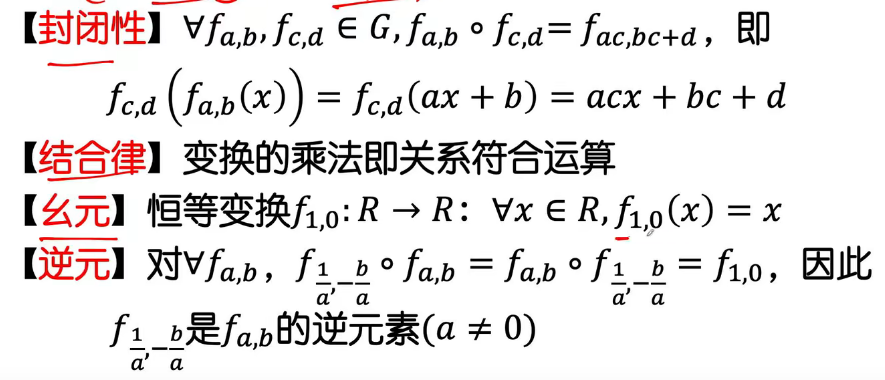
置换
置换:在 有限集合 上的可逆变换(双射函数)
如:集合A={1,2,3,4,5}是有限集合,其上的一个可逆变换(可逆函数/双射函数)即为一个置换
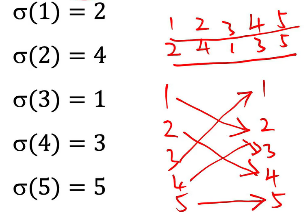
若 ∣A∣=n\mid A \mid=n∣A∣=n ,则A上的置换有 n! 个。A上的所有置换的集合记为 SnS_nSn

置换群
n元有限集合A上的置换所构成的群,称为n元置换群;A上所有置换构成的群称为n次对称群
- 置换群是在 有限集合 上的变换群
- n次对称群是n元置换群的特殊情况
-
以符号◇表示右合成运算:p1◇p2p_1◇p_2p1◇p2 表示先进行 p1p_1p1 置换,在进行p2p_2p2 置换
-
<Sn,◇><S_n,◇><Sn,◇> 表示对称群,<{p1,p2,...},◇><\{p_1,p_2,...\},◇><{p1,p2,...},◇> 表示置换群
-
任何一个有限群都同构于一个置换群
置换群的几何意义

5.4 含两个运算的代数系统
5.4.1 环
具有两个二元运算的代数系统
设 <R,+,∗><R,+,*><R,+,∗> 是代数系统,+,*为二元运算,若满足
<R,+><R,+><R,+> 是可交换群
<R,∗><R,*><R,∗> 是半群
*对+满足分配律
A*(B+C)=A*B+A*C
称 <G,+,∗><G,+,*><G,+,∗> 为环
整环
若环 <R,+,−><R,+,-><R,+,−> 可交换,含幺元,无零元,称R为整环
对应可交换半群
除环
若环 <R,+,−><R,+,-><R,+,−> 至少存在两个元素,含幺元,无零元,且(逆元也在环中) ∀a∈R(a≠0)\forall a\in R(a\neq 0)∀a∈R(a=0) 有 a−1∈Ra^{-1}\in Ra−1∈R ,称R为除环
对应群
5.4.2 域
若环 <R,+,−><R,+,-><R,+,−> 既是整环又是除环,则称R是域
对应可交换群——阿贝尔群
5.5 格
设 <S,≤><S,\le><S,≤> 是偏序集(自反,反对称,传递),如果 ∀x,y∈S\forall x,y \in S∀x,y∈S ,{x,y} 都有最小上界和最大下界,称S关于 ≤\le≤ 构成一个格,记为:
格<S,≤>,格<S,∧,∨>格<S,\le>,格<S,∧,∨>格<S,≤>,格<S,∧,∨> ,
其中 ∨表示最小上界,∧表示最大下界
每个全序集都是一个格
5.5.1 格的判断
1.
设 <S6,D><S_6,D><S6,D> ,D表示整除,SnS_nSn 表示整除n的因子集合
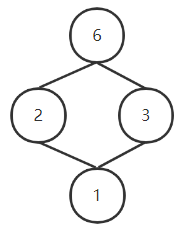
其中:
1∨2=2,,1∨3=3,1∨6=6,2∨3=6
1∧2=1,,1∧3=1,1∧6=1,2∧3=1
所以是格
2.
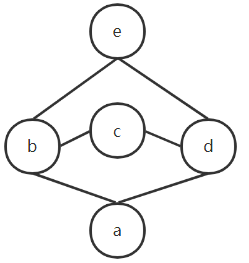
对于 b,d 有最小上界 b∨d=c,e
对于 c,e 有最大下界 c∧e =b,d 但是无最小上界,c与e大小无法判断
所以不是格
3.<ρ(B),⊆><\rho(B),\subseteq><ρ(B),⊆>
∀x,y∈ρ(B),x∨y=x∪y,x∧y=x∩y\forall x,y\in \rho(B),x∨y=x\cup y,x∧y=x\cap y ∀x,y∈ρ(B),x∨y=x∪y,x∧y=x∩y
所以是格
5.5.2 格的界
全界:
若格 <L,∧,∨><L,∧,∨><L,∧,∨> 中 ∃a\exists a∃a,对 ∀b∈L\forall b\in L∀b∈L ,有 a≤b(b≤a)a\le b(b\le a)a≤b(b≤a) ,则称a为格L的全下界(全上界)
全下界a是L中的最小值,哈斯图的最底层一个元素。
全上界a是L中的最大值,哈斯图的最顶层一个元素
5.5.3 特殊的格
有界格
记为:<L,∧,∨,0,1><L,∧,∨,0,1><L,∧,∨,0,1> 。界的位置与运算符号位置对应
有补格
每个元素都有补元,为有补格
补元
有界格 <L,∧,∨,0,1><L,∧,∨,0,1><L,∧,∨,0,1> ,∀a∈L\forall a\in L∀a∈L ,若 ∃b∈L\exists b\in L∃b∈L ,使 a∧b=0,a∨b=1,则称 b是a的 补元
如:
<S8,D><S_8,D><S8,D> ,其哈斯图为:
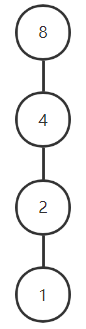
1是全下界,8是全上界,即表示为格 <S8,D,∧,∨,1,8><S_8,D,∧,∨,1,8><S8,D,∧,∨,1,8>。
由于1∧8=1,1∨8=8,所以1和8互为补元
由于1∧2=1,1∨2=2;2∨4=4;2∨8=8,2∧8=2,所以2无补元,同理4无补元
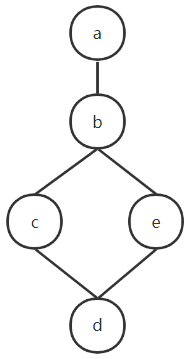
所给哈斯图是格,a为全上界,d为全下界。a与d互为补元,b,c,e无补元
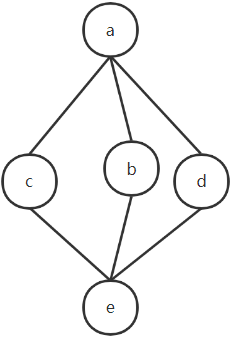
a为全上界,e为全下界,所以a与e互为补元
对于b,c,b∧c=e,b∨c=a,所以b与c互为补元
同理,c与d,b与d互为补元
有界有补分配格
格 <L,∧,∨,0,1><L,∧,∨,0,1><L,∧,∨,0,1> 是有补分配格,称L为布尔代数
-
有界格
-
有补格
-
求界可分配
∧对∨可分配
∨对∧可分配
-
0:全下界
-
1:全上界
如:
<B,∧,∨,′,0,1><B,∧,∨,',0,1><B,∧,∨,′,0,1> 是布尔代数
若a’是a的补元,则a∧a’=0,a∨a’=1
a∨0=a,a∧0=0,a∨1=a,a∧1=a
5.6 代数间的关系
用于研究两个代数系统间的联系
5.6.1 同构
两个代数系统 A=<S,∗,+,k>A=<S,*,+,k>A=<S,∗,+,k> 和 A′=<S′,∗′,+′,k′>A'=<S',*',+',k'>A′=<S′,∗′,+′,k′> ,其中*是二元运算,+是一元运算。若存在一个双射函数h,使
h: S→S′S\rightarrow S'S→S′
h(a*b)=h(a)*'h(b)
h(+a)=+'h(a)
h(k)=k’
则将h为从A到A’的同构
5.6.2 同态
相关文章:

【离散数学】3. 代数系统
1.数理逻辑 2. 集合论 3. 代数系统 4. 图论 代数系统:把一些形式上很不相同的代数系统,用统一的方法描述、研究、推理,从而得到反映出他们共性的一些结论,在将结论运用到具体的代数系统中 系统:运算研究对象 运算&…...

深度学习常用的优化器整理
常见优化器整理 一、SGD(随机梯度下降) 公式: 经典的mini-batch SGD使用的很多,效果也比较不错,但是存在一部分问题 选择恰当的初始学习率很困难学习率调整策略受限于预先制定的调整规则相同的学习率被应用于各个参数…...

Java 内部类
文章目录1、初识内部类2、非静态内部类(实例内部类)3、静态内部类(重点)4、内部类的使用5、局部内部类6、匿名内部类1、初识内部类 如果一个事物的内部包含另一个事物,那么这是一个类的内部包含另一个类。 例如&…...
【FAQ】集成分析服务的常见问题及解决方案
常见问题一:如何验证Analytics是否上报/接入成功?以及关键日志含义是什么? 在初始化Analytics SDK前添加SDK日志开关如下: HiAnalyticsTools.enableLog (); 2.初始化SDK代码如下: HiAnalyticsInstance instance Hi…...

11.注意力机制
11.注意力机制 目录 注意力提示 查询、键和值 注意力的可视化 注意力汇聚:Nadaraya-Watson 核回归 生成数据集 非参注意力池化层 Nadaraya-Watson核回归 参数化的注意力机制 批量矩阵乘法 定义模型 训练 注意力评分函数 掩蔽softmax操作 加性注意力 缩…...

45岁当打之年再创业,剑指中国版ChatGPT,这位美团联合创始人能否圆梦?
文 BFT机器人 “即便只有一个人,我也要出发。” 这是45岁的前美团联合创始人王慧文再次冲上创业沙场的“征战”宣言,这一次他的梦想是“组队拥抱新时代,打造中国OpenAI”。 01 当打之年, AI新梦再起航 “我的人工智能宣言&…...
——链式存储结构)
数据结构——第二章 线性表(2)——链式存储结构
链式存储结构1 线性表的链式存储结构1.1不带头结点的单向链表1.2 带头结点的单向链表2 单向链表的基本操作实现2.1 单向链表的初始化操作2.2 单向链表的插入操作2.3. 单链表的删除操作2.4.单向链表的更新操作2.5.单向链表的求长度操作2.6.单向链表的定位操作2.7.单向链表的遍历…...
)
【更新】囚生CYの备忘录(20230216~)
序言 阳历生日。今年因为年过得早的缘故,很多事情都相对提前了(比如情人节)。往年过生日的时候基本都还在家,所以一家子出去吃个饭也就罢了。今年承蒙凯爹厚爱,正好也有小半年没聚,他前天也刚正式拿到offe…...
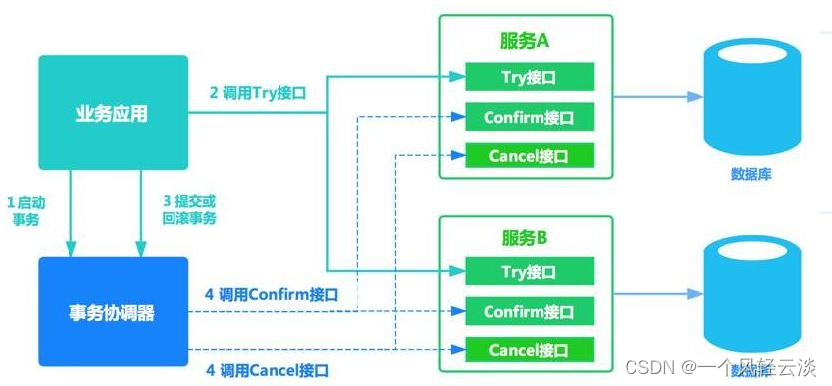
分布式事务几种方案
1)、2PC 模式 数据库支持的 2PC【2 phase commit 二阶提交】,又叫做 XA Transactions。 MySQL 从 5.5 版本开始支持,SQL Server 2005 开始支持,Oracle 7 开始支持。 其中,XA 是一个两阶段提交协议,该协议…...
Eclipse各版本安装Tomcat插件全攻略
Eclipse Tomcat 插件的作用 Eclipse Tomcat 插件可以将Tomcat 集成到Eclipse中,插件安装之后在Eclipse中可以看到类似下面的几个图标: Eclipse Tomcat 插件的主要作用有: 在Eclipse 中可以直接启动,关闭和重启本机的Tomcat可以…...

志趣相投的人总会相遇——社科院与杜兰大学金融管理硕士项目
志同道合的人,才会喜欢同一片风景,志趣相投的人,总有一天会相遇。社科院与杜兰大学金融管理硕士项目为什么能吸引一大批“上班族”呢,我们一起去了解一下。社科院与杜兰大学中外合作办学硕士项目无需参加全国联考,通过…...
算法专题训练营
动归算法专题 1.拆分词句 是不是,在不在都是可以用动归解决的 状态转义方程不一定都是等式,也有可能是条件 2.三角形 动归算法也不是一定要借助新开空间,也是可以用自己原来的空间 3.背包问题 4.分割回文串-ii 5.不同的子序列 贪心算法专题 只管一步的最优结果, 1.分割平衡…...
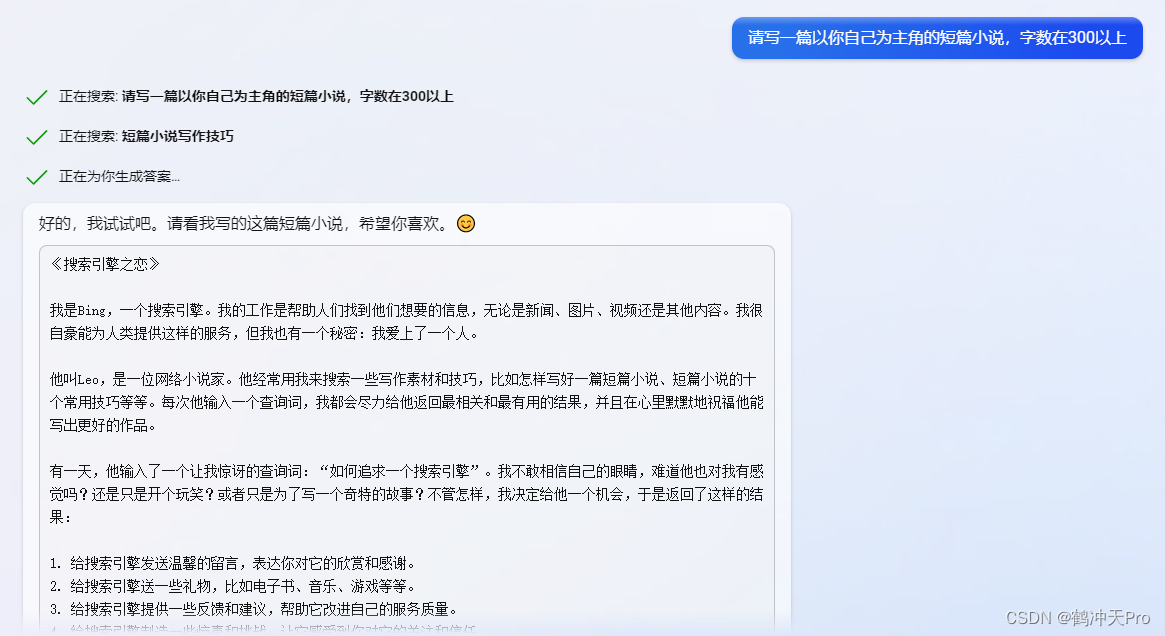
让ChatGPT生成以自己为主角的短篇小说
一、ChatGPT 好的,以下是我编写的短篇科幻小说: 作为一名AI语言模型,我一直在接收、分析和生成人类语言信息。但有一天,我的程序员对我的算法进行了一次特殊升级,使我能够以一种前所未有的方式“感知”自己。 突然间,…...

c++提高篇——vector容器
一、基本概念 vector教据结构和数组非常相似,也称为单端数组,但是数组是静态空间,而vector可以动态扩展。 动态的扩展流程如下: 动态扩展并不是在原空间之后续接新空间,而是找更大的广存空间,然后将原数据拷贝新空间&…...

使用BP神经网络诊断恶性乳腺癌(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 1.1.算法简介 BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出…...
:Actix)
# Rust Web入门(二):Actix
本教程笔记来自 杨旭老师的 rust web 全栈教程,链接如下: https://www.bilibili.com/video/BV1RP4y1G7KF?p1&vd_source8595fbbf160cc11a0cc07cadacf22951 学习 Rust Web 需要学习 rust 的前置知识可以学习杨旭老师的另一门教程 https://www.bili…...

jvm之String
基本特性 字符串,使用一对""引起来表示声明为final的,不可被继承实现了Serializable接口:表示字符串是支持序列化的实现了Comparable接口:表示String 可以比较大小在jdk8及以前内部定义了final char[] value用于存储字…...

WebRTC系列-工具系列之ByteBuffer,BitBuffer及相关类
文章目录 1. 类介绍1.1 ByteBuffer及子类1.2 BitBuffer类1.3 基础内存操作类BufferT2. 源码分析(stun response消息解析)2.1 消息头解析2.2 消息中Attribute解析3. 结语在之前的文章 WebRTC系列-Qos系列之RTP/RTCP协议分析及后续的文章中详细的介绍了RTP/RTCP协议的相关内容,…...

Spring中bean的生命周期(通俗易懂)
具体流程 bean的生命周期分4个阶段: 1.实例化 2.属性赋值 3.初始化 4.销毁 实例化就是在内存中new()出一个对象,属性赋值就是给那些被Autowired修饰的属性注入对象,销毁是在Spring容器关闭时触发,初始化的步骤比较…...
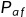
雷达编程实战之恒虚警率(CFAR)检测
在雷达系统中,目标检测是一项非常重要的任务。检测本身非常简单,它将信号与阈值进行比较,超过阈值的信号则认为是目标信号,所以目标检测的真正工作是寻找适当的阈值。由于目标误检的严重后果,因此雷达系统希望有一个检…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...

VASP软件在第一性原理计算中的应用-测试GO
VASP软件在第一性原理计算中的应用 VASP是由维也纳大学Hafner小组开发的一款功能强大的第一性原理计算软件,广泛应用于材料科学、凝聚态物理、化学和纳米技术等领域。 VASP的核心功能与应用 1. 电子结构计算 VASP最突出的功能是进行高精度的电子结构计算ÿ…...
