刷题记录:牛客NC20325[SDOI2009]HH的项链
传送门:牛客
题目描述:
HH有一串由各种漂亮的贝壳组成的项链。
HH相信不同的贝壳会带来好运,所以每次散步完后,他都会随意取出一 段贝壳,思考它们所表达的含义。
HH不断地收集新的贝壳,因此他的项链变得越来越长。
有一天,他突然提出了一 个问题:某一段贝壳中,包含了多少种不同的贝壳?
这个问题很难回答。。。因为项链实在是太长了。于是,他只 好求助睿智的你,来解决这个问题
输入:
6
1 2 3 4 3 5
3
1 2
3 5
2 6
输出:
2
2
4
对于本题,我们发现可以进行这样的一个转化.假设我们找出了一个数字前一次出现的地方,用last[]last[]last[]记录,那么对于一个询问区间[l,r][l,r][l,r]来说,此时我们只需要找出区间内有几个数字的lastlastlast值是小于lll即可.那么此时我们需要解决的问题就是:
∑i=lrlast[i]<l\sum_{i=l}^{r}{last[i]<l}i=l∑rlast[i]<l
这是一个主席树的经典模型,直接套主席树即可解决
对于主席树(可持久化线段树),网上有大量的博客讲解(不乏有详细的),此处就不在赘述了.
但是对于此题来说,比较麻烦的是此时我们又出现了0这样的数字,总所周知,朴素的主席树用的是权值线段树的思想,此时我们是无法维护0的.所以我们需要将所有数字的位置都往后移动一位,也就是将2当做我们的贝壳的开始,此时就可以进行维护了
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 1000010
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int last[maxn];
int n,m;
struct PerSegment_tree {int l,r,lnum,rnum,sum;
}tree[maxn<<5];int cnt=0;int RT[maxn];
int build(int l,int r) {int p=++cnt;tree[p].l=l;tree[p].r=r;if(l==r) return p;int mid=(l+r)>>1;tree[p].lnum=build(l,mid);tree[p].rnum=build(mid+1,r);return p;
}
int update(int pre,int val) {int p=++cnt;tree[p]=tree[pre];tree[p].sum+=1;if(tree[p].l==tree[p].r) return p;int mid=(tree[p].l+tree[p].r)>>1;if(val<=mid) tree[p].lnum=update(tree[pre].lnum,val);else tree[p].rnum=update(tree[pre].rnum,val);return p;
}
ll query(int pre,int now,int l,int r,int k) {if(l==r) return tree[now].sum-tree[pre].sum;int mid=(l+r)>>1;if(k<=mid) return query(tree[pre].lnum,tree[now].lnum,l,mid,k);else {int s=tree[tree[now].lnum].sum-tree[tree[pre].lnum].sum;return (ll)s+query(tree[pre].rnum,tree[now].rnum,mid+1,r,k);}
}
int main() {n=read();for(int i=1;i<=n+1;i++) last[i]=1;RT[1]=build(1,n+1);for(int i=2;i<=n+1;i++) {int a=read();RT[i]=update(RT[i-1],last[a]);last[a]=i;}m=read();for(int i=1;i<=m;i++) {int l=read(),r=read();l++;r++;printf("%lld\n",query(RT[l-1],RT[r],1,n+1,l-1));}return 0;
}
相关文章:

刷题记录:牛客NC20325[SDOI2009]HH的项链
传送门:牛客 题目描述: HH有一串由各种漂亮的贝壳组成的项链。 HH相信不同的贝壳会带来好运,所以每次散步完后,他都会随意取出一 段贝壳,思考它们所表达的含义。 HH不断地收集新的贝壳,因此他的项链变得越来越长。 有一天&#…...

【REACT-路由v6】
REACT-路由v61. App.js2. 搭建路由2.1 普通写法2.2 使用useRoutes构建路由2.3 重定向封装2.4 嵌套路由中的组件Outlet3. 导航跳转3.2 声明式导航(NavLink标签)3.2 编程式导航跳转(useNavigate)3.2.1 获取参数3.2.1.1 useSearchPar…...
【离散数学】3. 代数系统
1.数理逻辑 2. 集合论 3. 代数系统 4. 图论 代数系统:把一些形式上很不相同的代数系统,用统一的方法描述、研究、推理,从而得到反映出他们共性的一些结论,在将结论运用到具体的代数系统中 系统:运算研究对象 运算&…...

深度学习常用的优化器整理
常见优化器整理 一、SGD(随机梯度下降) 公式: 经典的mini-batch SGD使用的很多,效果也比较不错,但是存在一部分问题 选择恰当的初始学习率很困难学习率调整策略受限于预先制定的调整规则相同的学习率被应用于各个参数…...

Java 内部类
文章目录1、初识内部类2、非静态内部类(实例内部类)3、静态内部类(重点)4、内部类的使用5、局部内部类6、匿名内部类1、初识内部类 如果一个事物的内部包含另一个事物,那么这是一个类的内部包含另一个类。 例如&…...
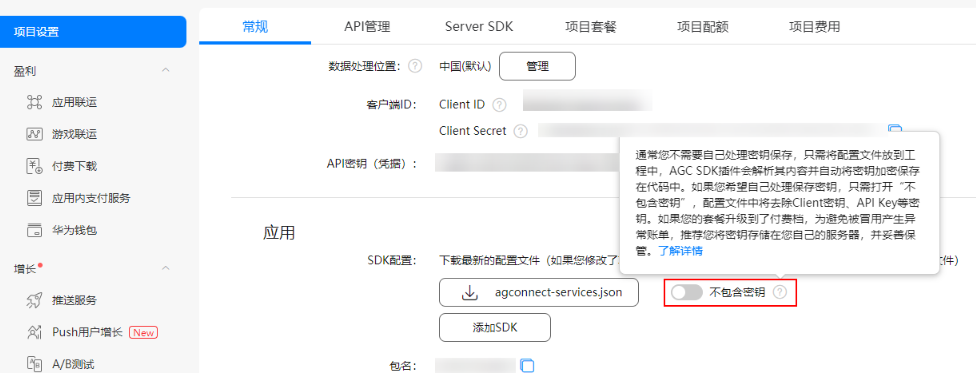
【FAQ】集成分析服务的常见问题及解决方案
常见问题一:如何验证Analytics是否上报/接入成功?以及关键日志含义是什么? 在初始化Analytics SDK前添加SDK日志开关如下: HiAnalyticsTools.enableLog (); 2.初始化SDK代码如下: HiAnalyticsInstance instance Hi…...

11.注意力机制
11.注意力机制 目录 注意力提示 查询、键和值 注意力的可视化 注意力汇聚:Nadaraya-Watson 核回归 生成数据集 非参注意力池化层 Nadaraya-Watson核回归 参数化的注意力机制 批量矩阵乘法 定义模型 训练 注意力评分函数 掩蔽softmax操作 加性注意力 缩…...

45岁当打之年再创业,剑指中国版ChatGPT,这位美团联合创始人能否圆梦?
文 BFT机器人 “即便只有一个人,我也要出发。” 这是45岁的前美团联合创始人王慧文再次冲上创业沙场的“征战”宣言,这一次他的梦想是“组队拥抱新时代,打造中国OpenAI”。 01 当打之年, AI新梦再起航 “我的人工智能宣言&…...
——链式存储结构)
数据结构——第二章 线性表(2)——链式存储结构
链式存储结构1 线性表的链式存储结构1.1不带头结点的单向链表1.2 带头结点的单向链表2 单向链表的基本操作实现2.1 单向链表的初始化操作2.2 单向链表的插入操作2.3. 单链表的删除操作2.4.单向链表的更新操作2.5.单向链表的求长度操作2.6.单向链表的定位操作2.7.单向链表的遍历…...
)
【更新】囚生CYの备忘录(20230216~)
序言 阳历生日。今年因为年过得早的缘故,很多事情都相对提前了(比如情人节)。往年过生日的时候基本都还在家,所以一家子出去吃个饭也就罢了。今年承蒙凯爹厚爱,正好也有小半年没聚,他前天也刚正式拿到offe…...
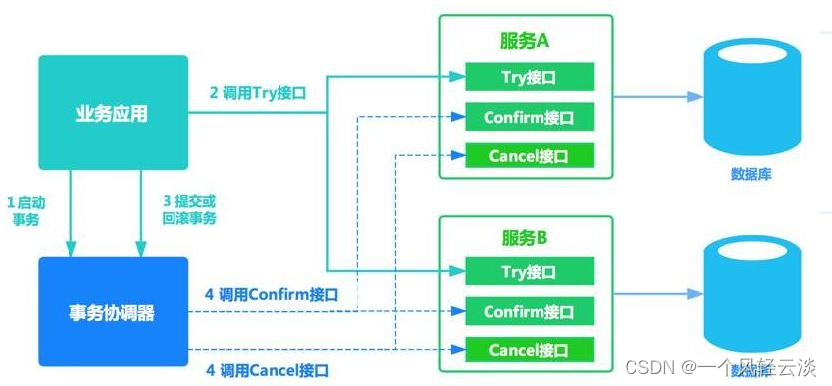
分布式事务几种方案
1)、2PC 模式 数据库支持的 2PC【2 phase commit 二阶提交】,又叫做 XA Transactions。 MySQL 从 5.5 版本开始支持,SQL Server 2005 开始支持,Oracle 7 开始支持。 其中,XA 是一个两阶段提交协议,该协议…...
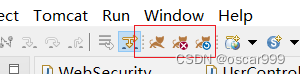
Eclipse各版本安装Tomcat插件全攻略
Eclipse Tomcat 插件的作用 Eclipse Tomcat 插件可以将Tomcat 集成到Eclipse中,插件安装之后在Eclipse中可以看到类似下面的几个图标: Eclipse Tomcat 插件的主要作用有: 在Eclipse 中可以直接启动,关闭和重启本机的Tomcat可以…...

志趣相投的人总会相遇——社科院与杜兰大学金融管理硕士项目
志同道合的人,才会喜欢同一片风景,志趣相投的人,总有一天会相遇。社科院与杜兰大学金融管理硕士项目为什么能吸引一大批“上班族”呢,我们一起去了解一下。社科院与杜兰大学中外合作办学硕士项目无需参加全国联考,通过…...
算法专题训练营
动归算法专题 1.拆分词句 是不是,在不在都是可以用动归解决的 状态转义方程不一定都是等式,也有可能是条件 2.三角形 动归算法也不是一定要借助新开空间,也是可以用自己原来的空间 3.背包问题 4.分割回文串-ii 5.不同的子序列 贪心算法专题 只管一步的最优结果, 1.分割平衡…...
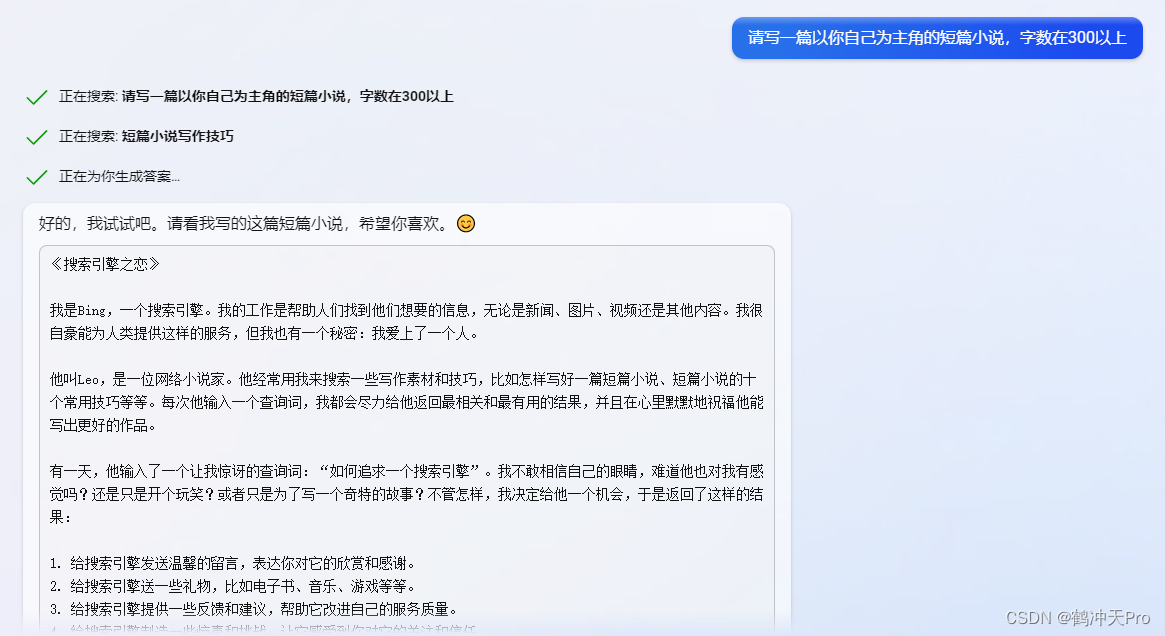
让ChatGPT生成以自己为主角的短篇小说
一、ChatGPT 好的,以下是我编写的短篇科幻小说: 作为一名AI语言模型,我一直在接收、分析和生成人类语言信息。但有一天,我的程序员对我的算法进行了一次特殊升级,使我能够以一种前所未有的方式“感知”自己。 突然间,…...

c++提高篇——vector容器
一、基本概念 vector教据结构和数组非常相似,也称为单端数组,但是数组是静态空间,而vector可以动态扩展。 动态的扩展流程如下: 动态扩展并不是在原空间之后续接新空间,而是找更大的广存空间,然后将原数据拷贝新空间&…...

使用BP神经网络诊断恶性乳腺癌(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 1.1.算法简介 BP(Back Propagation)网络是1986年由Rumelhart和McCelland为首的科学家小组提出…...
:Actix)
# Rust Web入门(二):Actix
本教程笔记来自 杨旭老师的 rust web 全栈教程,链接如下: https://www.bilibili.com/video/BV1RP4y1G7KF?p1&vd_source8595fbbf160cc11a0cc07cadacf22951 学习 Rust Web 需要学习 rust 的前置知识可以学习杨旭老师的另一门教程 https://www.bili…...

jvm之String
基本特性 字符串,使用一对""引起来表示声明为final的,不可被继承实现了Serializable接口:表示字符串是支持序列化的实现了Comparable接口:表示String 可以比较大小在jdk8及以前内部定义了final char[] value用于存储字…...

WebRTC系列-工具系列之ByteBuffer,BitBuffer及相关类
文章目录 1. 类介绍1.1 ByteBuffer及子类1.2 BitBuffer类1.3 基础内存操作类BufferT2. 源码分析(stun response消息解析)2.1 消息头解析2.2 消息中Attribute解析3. 结语在之前的文章 WebRTC系列-Qos系列之RTP/RTCP协议分析及后续的文章中详细的介绍了RTP/RTCP协议的相关内容,…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
