计算机安全学习笔记(III):强制访问控制 - MAC
基本概念
强制访问控制是一种高级访问控制机制,旨在通过强制执行事先定义的安全策略,实现资源和信息的严格保护。与自主访问控制(Discretionary Access Control,DAC)不同,MAC 的控制权不由用户自身决定,而是由预设的规则和安全策略来主导。这意味着即使用户具有足够的权限,也不能违背MAC所规定的规则。
机制与结构
- 标签和分类:MAC 的核心在于标签化,它通过为每个主体、资源和对象分配标签来定义其安全等级或分类。这些标签通常包括了机密性、完整性和可用性等信息。例如,一个文件可以被标记为“机密”级别,只有具有相应标签的主体才能访问该文件。每个主体和资源都被分配一个标签,通常是安全级别、权限或分类信息。这些标签用于指示主体可以访问哪些资源。
- 安全策略:系统管理员制定安全策略,规定了标签之间的访问规则。这些规则是强制性的,不受主体自身意愿的影响。
- 多级安全:MAC 可以实现多级安全,确保高级别的主体无法访问低级别的资源,但低级别主体可以访问高级别资源的情况。
MAC的优势与挑战
尽管强制访问控制为信息安全带来了诸多优势,但它也不是万能的,有其适用场景和局限性。
优势:
- 强大的安全性:强制访问控制通过强制执行严格的安全策略,有效地防止了未经授权的访问,从而提供了高度的数据和资源保护。
- 减少人为因素:由于访问控制由预定义的规则驱动,减少了用户主观判断和错误配置带来的安全风险。
- 满足法规合规性:对于某些领域和组织,如政府机构和金融机构,强制访问控制有助于满足法规和合规性要求。
挑战:
- 复杂性:强制访问控制的实施和管理需要深入的安全专业知识,可能增加系统复杂性,使其难以维护
- 用户适应性:由于访问控制是基于预定策略的,可能会对用户的日常操作产生影响,导致适应性问题。
- 性能影响:强制执行的访问控制可能会对系统性能产生影响,特别是在访问请求频繁的情况下,需要权衡安全性和性能。
相关文章:
:强制访问控制 - MAC)
计算机安全学习笔记(III):强制访问控制 - MAC
基本概念 强制访问控制是一种高级访问控制机制,旨在通过强制执行事先定义的安全策略,实现资源和信息的严格保护。与自主访问控制(Discretionary Access Control,DAC)不同,MAC 的控制权不由用户自身决定&am…...

java判断ip是否为指定网段
具体网络知识原理请看这个博文 /**** param address servletRequest.getRemoteAddr();* param host servletRequest.getRemoteHost();* return* Description 检验IP是否符合安全限定*/private boolean ipIsInNet(String address, String host){Set<String> iPset allow…...

如何通过人工智能和自动化提高供应链弹性?
全球供应链中的数字化转型已经引起了广泛关注,尽管在过去的十年中,这一话题被广泛讨论,但许多公司仍然对如何实现这一不明确的目标感到困惑。人们普遍认识到这种转变的重要性,而新冠疫情及其带来的巨大影响也为行业向数字化转型方…...

【Apollo学习笔记】——规划模块TASK之PATH_REUSE_DECIDER
文章目录 前言PATH_REUSE_DECIDER功能简介PATH_REUSE_DECIDER相关配置PATH_REUSE_DECIDER总体流程PATH_REUSE_DECIDER相关子函数IsCollisionFreeTrimHistoryPathIsIgnoredBlockingObstacle和GetBlockingObstacleS Else参考 前言 在Apollo星火计划学习笔记——Apollo路径规划算…...

框架分析(6)-Ruby on Rails
框架分析(6)-Ruby on Rails 专栏介绍Ruby on Rails核心概念以及组件讲解MVC架构模式约定优于配置强大的ORM支持自动化测试丰富的插件生态系统RESTful路由安全性总结 优缺点优点快速开发简单易学MVC架构强大的ORM支持大量的插件和Gem支持 缺点性能问题学习…...

LLMs NLP模型评估Model evaluation ROUGE and BLEU SCORE
在整个课程中,你看到过类似模型在这个任务上表现良好,或者这个微调模型在性能上相对于基础模型有显著提升等陈述。 这些陈述是什么意思?如何形式化你的微调模型在你起初的预训练模型上的性能改进?让我们探讨一些由大型语言模型开…...

BlazorServer中C#与JavaScript的相互调用
BlazorServer中C#与JavaScript的相互调用 前言: 虽然BlazorServer中推荐使用C#在razor页面中的替代JavaScript来完成逻辑的编写,但当需要使用第三方的javascript文件/组件里的内容时,则难免要在C#中调用其方法或对象。反之当你的(用到第…...

深入理解 MD5 消息摘要算法和在密码存储中的应用及安全隐患
MD5 算法相信很多开发人员都听说过, 一个最常见的使用到它的地方就是密码的存储. 当然, 很多人会说, 这个算法已经不太安全了, 确实如果你想更安全的保存密码, 则应该考虑其它更安全的算法, 不过这不属于此次讨论的主题. 什么是 MD5 MD5 是一种算法, MD5 中的 MD 代表 Message…...
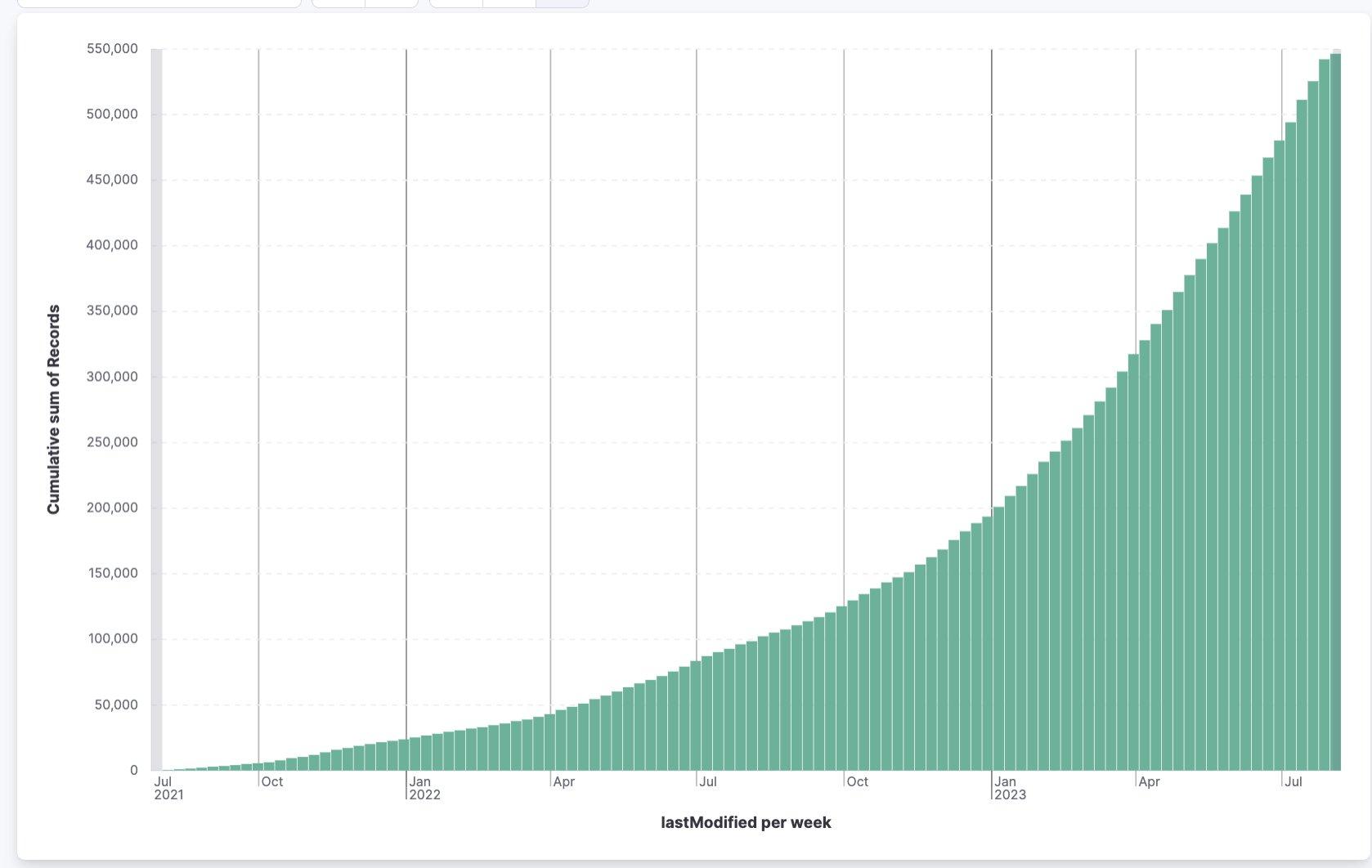
python网络爬虫指南二:多线程网络爬虫、动态内容爬取(待续)
文章目录 一、多线程网络爬虫1.1 线程的基础内容、GIL1.2 创建线程的两种方式1.3 threading.Thread类1.4 线程常用方法和锁机制1.5 生产者-消费者模式1.5.1 生产者-消费者模式简介1.5.2 Condition 类协调线程 1.6 线程中的安全队列1.6 多线程爬取王者荣耀壁纸1.6.1 网页分析1.6…...

华为AirEgine9700S AC配置示例
Vlan97为管理Vlan <AirEgine9700S>dis cu Software Version V200R021C00SPC100 #sysname AirEgine9700S #http timeout 60http secure-server ssl-policy default_policyhttp secure-server server-source -i allhttp server enable #set np rss hash-mode 5-tuple # md…...

VUE3基础
一、vue-router v4.x 介绍 | Vue Router 1、安装 yarn add vue-routernext next代表最新的版本 2、路由配置 在src目录下,新建router/index.ts,具体配置如下 import {RouteRecordRaw,createRouter,createWebHashHistory} from vue-router const r…...
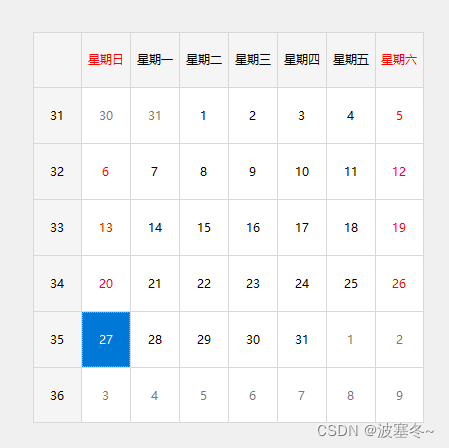
Qt应用开发(基础篇)——日历 QCalendarWidget
一、前言 QCalendarWidget类继承于QWidget,是Qt设计用来让用户更直观的选择日期的窗口部件。 时间微调输入框 QCalendarWidget根据年份和月份初始化,程序员也通过提供公共函数去改变他们,默认日期为当前的系统时间,用户通过鼠标和…...

Python学习笔记:正则表达式、逻辑运算符、lamda、二叉树遍历规则、类的判断
1.正则表达式如何写? 序号实例说明1.匹配任何字符(除换行符以外)2\d等效于[0-9],匹配数字3\D等效于[^0-9],匹配非数字4\s等效于[\t\r\n\f],匹配空格字符5\S等效于[^\t\r\n\f],匹配非空格字符6\w等效于[A-Za-z0-9]&…...

【滑动窗口】leetcode1004:最大连续1的个数
一.题目描述 最大连续1的个数 这道题要我们找最大连续1的个数,看到“连续”二字,我们要想到滑动窗口的方法。滑动窗口的研究对象是一个连续的区间,这个区间需要满足某个条件。那么本题要找的是怎样的区间呢?是一个通过翻转0后得到…...
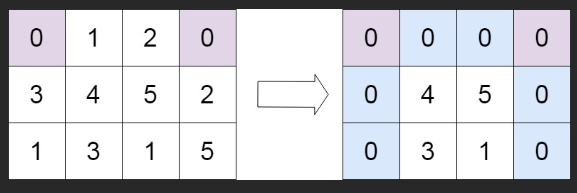
力扣:73. 矩阵置零(Python3)
题目: 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 来源:力扣(LeetCode) 链接:力扣(LeetCode)官网 - 全球极客挚…...

VB|基础语法 变量定义 函数定义 循环语句 IF判断语句等
文章目录 变量定义函数定义控制台输入输出switch case语句IF语句FOR循环语句不等于逻辑运算符 变量定义 int Dim 变量名 As Int32 0 string Dim 变量名 As String "" bool Dim 变量名 As Boolean False 枚举 Dim 变量名 As 枚举名 数组 Dim array(256) As String…...

Github 博客搭建
Github 博客搭建 准备工作 准备一个 github 账号;建立 github 仓库,仓库名为 username.github.io,同时设置仓库为 public;clone 仓库,写入一个 index.html 文件,推送到仓库(许多网上的教程会有…...
:通过交叉验证网格搜索机器学习的最优参数)
模型预测笔记(三):通过交叉验证网格搜索机器学习的最优参数
文章目录 网络搜索介绍步骤参数代码实现 网络搜索 介绍 网格搜索(Grid Search)是一种超参数优化方法,用于选择最佳的模型超参数组合。在机器学习中,超参数是在训练模型之前设置的参数,无法通过模型学习得到。网格搜索…...
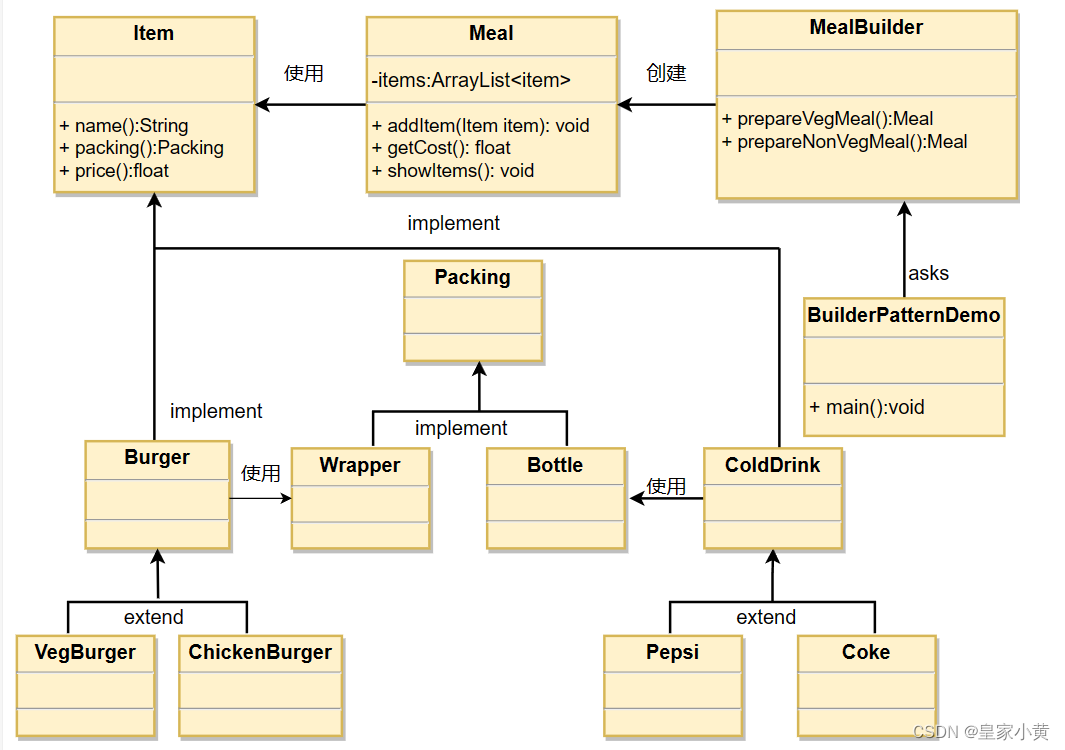
创建型模式-建造者模式
使用多个简单的对象一步一步构建成一个复杂的对象 主要解决:主要解决在软件系统中,有时候面临着"一个复杂对象"的创建工作,其通常由各个部分的子对象用一定的算法构成;由于需求的变化,这个复杂对象的各个部…...
Rust常用加密算法
哈希运算(以Sha256为例) main.rs: use crypto::digest::Digest;use crypto::sha2::Sha256;fn main() { let input "dashen"; let mut sha Sha256::new(); sha.input_str(input); println!("{}", sha.result_str());} Cargo.toml: [package]n…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
