【滑动窗口】leetcode1004:最大连续1的个数
一.题目描述
最大连续1的个数

这道题要我们找最大连续1的个数,看到“连续”二字,我们要想到滑动窗口的方法。滑动窗口的研究对象是一个连续的区间,这个区间需要满足某个条件。那么本题要找的是怎样的区间呢?是一个通过翻转0后得到连续1的区间,而最多可以翻转k个字符。
故要找的是包含0的个数不超过k的区间,因为如果超过k个0,即使经过翻转,该区间的1也还是不连续。
题意转化过来后,本题便不再困难。
二.思路分析
滑动窗口是在暴力解法的基础上优化过来的。本题的暴力解法就是两层for循环枚举所有的区间,找出满足条件的区间,通过比较得到最长的区间长度,结果就是数组中连续1的最大个数。
class Solution {
public:int longestOnes(vector<int>& nums, int k) {int n = nums.size();int ret = 0;for (int left = 0; left < n; left++){int zero = 0;//记录0的个数for (int right = left; right < n; right++){if (nums[right] == 0){zero++;}//如果0的个数已经超过k,right向后枚举的区间肯定也不符合要求if (zero > k){break;}ret = max(ret, right - left + 1);}}return ret;}
};要想用滑动窗口,首先要证明right没有回退的必要
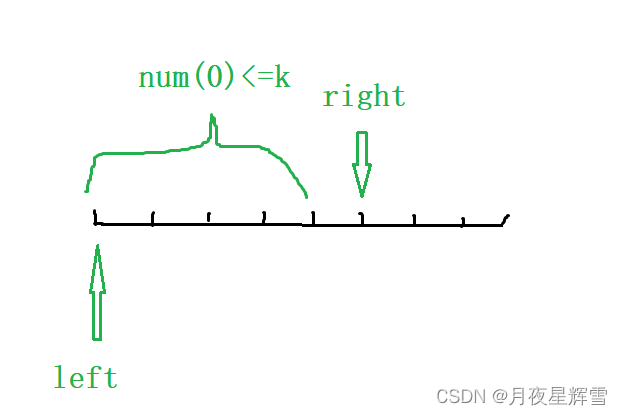
如图,right从left位置出发,依次向后枚举,到图中的位置[left, right]区间内0的个数大于k,停了下来。这说明[left, right - 1]区间是满足要求的。
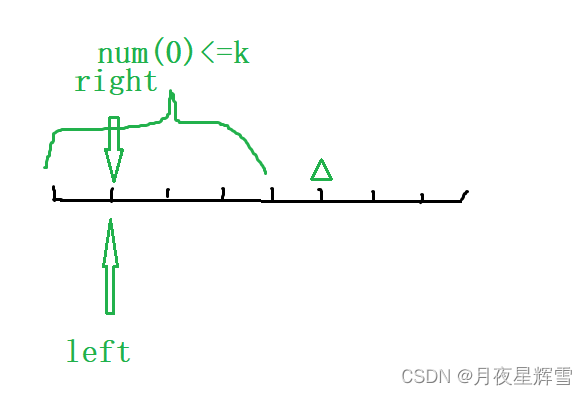
按照暴力枚举策略,left向右移动一步,right回退到left位置。但最终right还是会回到原来的标记处。因为通过上一轮枚举,我们可知图中大括号标记的区间都是符合条件的,而right只有在区间不满足要求时才会停下。所以right没有必要回退,留在原地即可。

那么此时[left, right]区间是否符合条件呢?答案是不一定。因为可能left跳过的是一个1, 0的数量并没有减少,也有可能跳过了一个0,区间内刚好有k个0。
当区间符合条件时,我们让right继续向后移动,接下来的步骤就和上面一样了。当区间不符合条件时,right向后枚举的区间就更不满足了,所以我们让left继续向右移动,直到区间满足要求为止。
故判断应该是一个循环语句,不能简单地只判断一次。
三.代码编写

按照滑动窗口的模版,找到各个条件即可。当枚举的情况满足要求时应该更新结果。什么时候满足要求呢?
1.进窗口之后,zero>=k,符合要求
2.进窗口之后,zero<k,经过若干次出窗口操作后,zero=k ,满足要求
故更新结果应放在整个循环的最后面
class Solution {
public:int longestOnes(vector<int>& nums, int k) {int n =nums.size();int zero = 0;//记录窗口内0的个数int left = 0, right = 0;int ret = 0;while (right < n){//进窗口if (nums[right] == 0){zero++;}//判断while (zero > k){//出窗口if (nums[left] == 0){zero--;}left++;}//更新结果ret = max(ret, right - left + 1);right++;}return ret;}
};时间复杂度O(n),相比于暴力枚举的O(n^2)提升了不少。
相关文章:

【滑动窗口】leetcode1004:最大连续1的个数
一.题目描述 最大连续1的个数 这道题要我们找最大连续1的个数,看到“连续”二字,我们要想到滑动窗口的方法。滑动窗口的研究对象是一个连续的区间,这个区间需要满足某个条件。那么本题要找的是怎样的区间呢?是一个通过翻转0后得到…...
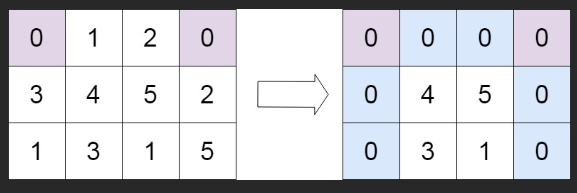
力扣:73. 矩阵置零(Python3)
题目: 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。 来源:力扣(LeetCode) 链接:力扣(LeetCode)官网 - 全球极客挚…...

VB|基础语法 变量定义 函数定义 循环语句 IF判断语句等
文章目录 变量定义函数定义控制台输入输出switch case语句IF语句FOR循环语句不等于逻辑运算符 变量定义 int Dim 变量名 As Int32 0 string Dim 变量名 As String "" bool Dim 变量名 As Boolean False 枚举 Dim 变量名 As 枚举名 数组 Dim array(256) As String…...

Github 博客搭建
Github 博客搭建 准备工作 准备一个 github 账号;建立 github 仓库,仓库名为 username.github.io,同时设置仓库为 public;clone 仓库,写入一个 index.html 文件,推送到仓库(许多网上的教程会有…...
:通过交叉验证网格搜索机器学习的最优参数)
模型预测笔记(三):通过交叉验证网格搜索机器学习的最优参数
文章目录 网络搜索介绍步骤参数代码实现 网络搜索 介绍 网格搜索(Grid Search)是一种超参数优化方法,用于选择最佳的模型超参数组合。在机器学习中,超参数是在训练模型之前设置的参数,无法通过模型学习得到。网格搜索…...
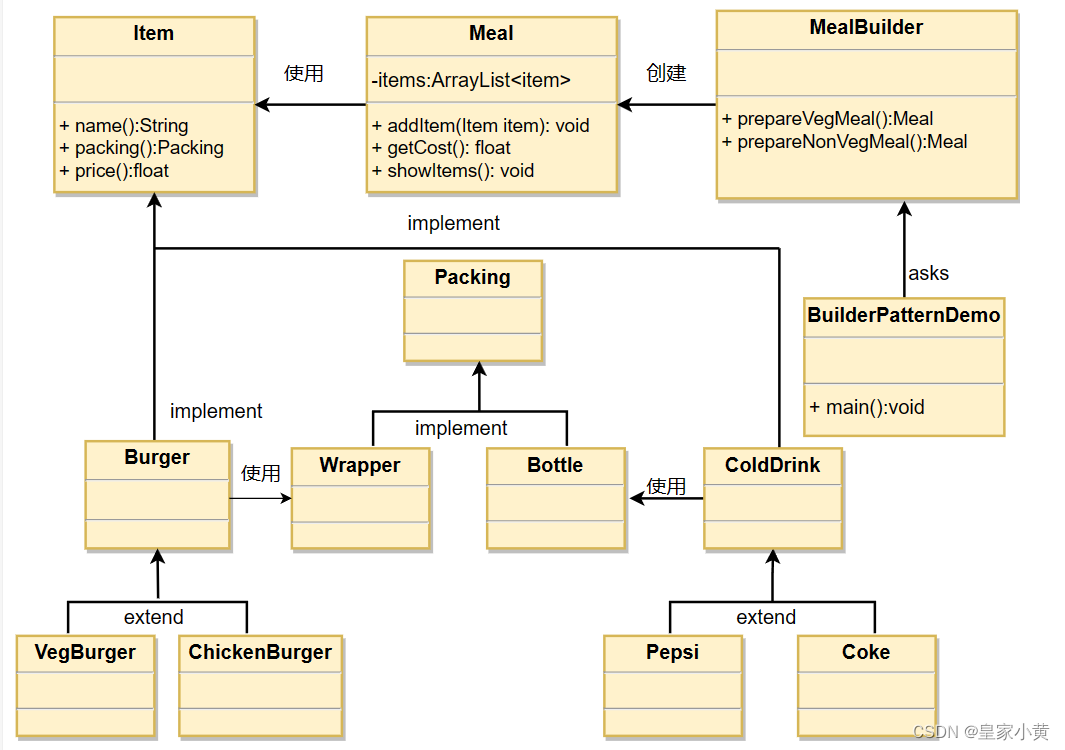
创建型模式-建造者模式
使用多个简单的对象一步一步构建成一个复杂的对象 主要解决:主要解决在软件系统中,有时候面临着"一个复杂对象"的创建工作,其通常由各个部分的子对象用一定的算法构成;由于需求的变化,这个复杂对象的各个部…...
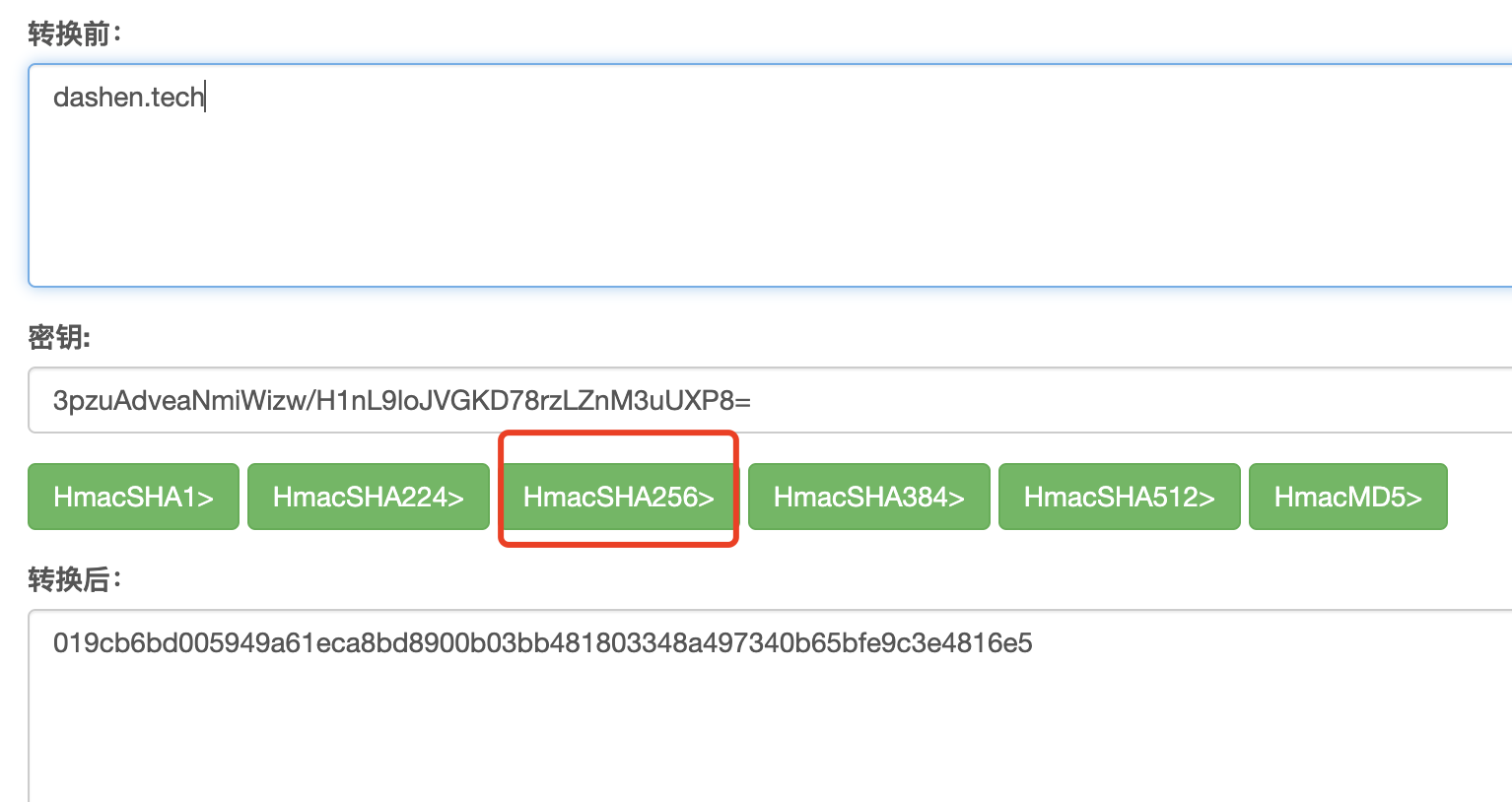
Rust常用加密算法
哈希运算(以Sha256为例) main.rs: use crypto::digest::Digest;use crypto::sha2::Sha256;fn main() { let input "dashen"; let mut sha Sha256::new(); sha.input_str(input); println!("{}", sha.result_str());} Cargo.toml: [package]n…...

[管理与领导-55]:IT基层管理者 - 扩展技能 - 1 - 时间管理 -2- 自律与自身作则,管理者管好自己时间的五步法
前言: 管理好自己的时间,不仅仅是理念,也是方法和流程。 步骤1:理清各种待办事项 当提到工作事项时,这通常指的是要完成或处理的工作任务或事务。这些事项可以包括以下内容: 任务分配:根据工作…...
--判断题)
电子商务员考试题库及答案(中级)--判断题
电子商务员题库 一、判断题 1.EDI就是按照商定的协议,将商业文件分类,并通过计算机网络,在贸易伙伴的计算机网络系统之间进行数据交换和自动处理。〔〕 2.相互通信的EDI的用户必须使用相同类型的计算机。〔 〕 3.EDI采用共同…...

(WAF)Web应用程序防火墙介绍
(WAF)Web应用程序防火墙介绍 1. WAF概述 Web应用程序防火墙(WAF)是一种关键的网络安全解决方案,用于保护Web应用程序免受各种网络攻击和威胁。随着互联网的不断发展,Web应用程序变得越来越复杂&#x…...

SpringMVC拦截器常见应用场景
在Spring MVC中,拦截器是通过实现HandlerInterceptor接口来定义的。该接口包含了三个方法: preHandle:在请求到达处理器之前执行,可以进行一些预处理操作。如果返回false,则请求将被拦截,不再继续执行后续的…...
爬虫:绕过5秒盾Cloudflare和DDoS-GUARD
本文章仅供技术研究参考,勿做它用! 5秒盾的特点 <title>Just a moment...</title> 返回的页面中不是目标数据,而是包含上面的代码:Just a moment... 或者第一次打开网页的时候: 这几个特征就是被Cloud…...

数据仓库环境下的超市进销存系统结构
传统的进销存系统建立的以单一数据库为中心的数据组织模式,已经无 法满足决策分析对数据库系统的要求,而数据仓库技术的出现和发展,为上述问题 的解决提供了强有力的工具和手段。数据仓库是一种对多个分布式的、异构的数据 库提供统一查询…...
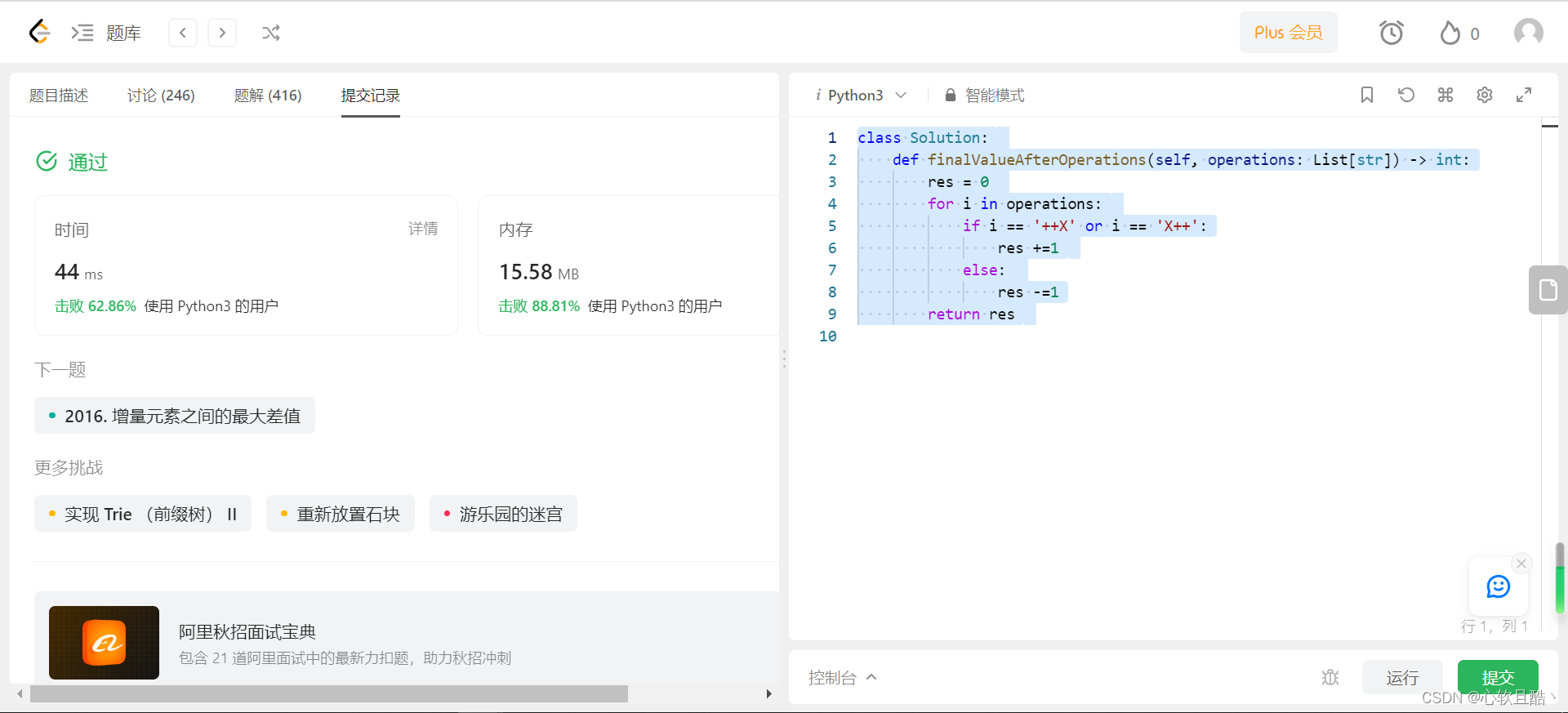
leetcode:2011. 执行操作后的变量值(python3解法)
难度:简单 存在一种仅支持 4 种操作和 1 个变量 X 的编程语言: X 和 X 使变量 X 的值 加 1--X 和 X-- 使变量 X 的值 减 1 最初,X 的值是 0 给你一个字符串数组 operations ,这是由操作组成的一个列表,返回执行所有操作…...

ubuntu下mysql
安装: sudo apt update sudo apt install my_sql 安装客户端: sudo apt-get install mysql-client sudo apt-get install libmysqlclient-dev 启动服务 启动方式之一: sudo service mysql start 检查服务器状态方式之一:sudo …...
-[链与索引:检索式问答])
大模型从入门到应用——LangChain:链(Chains)-[链与索引:检索式问答]
分类目录:《大模型从入门到应用》总目录 下面这个示例展示了如何在索引上进行问答: from langchain.embeddings.openai import OpenAIEmbeddings from langchain.vectorstores import Chroma from langchain.text_splitter import CharacterTextSplitte…...
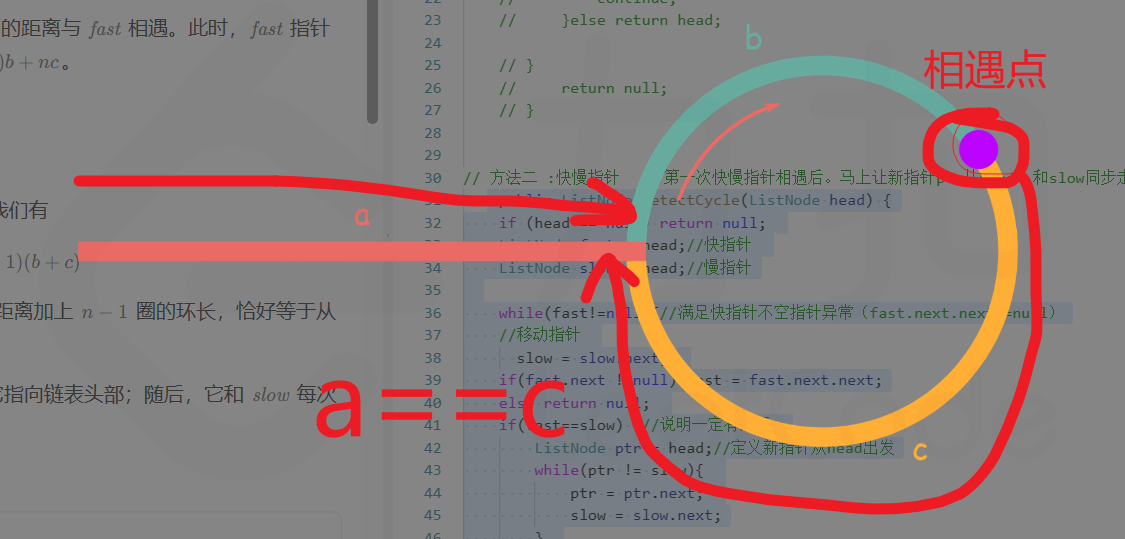
【LeetCode-中等题】142. 环形链表 II
文章目录 题目方法一:哈希表set去重方法二:快慢指针 题目 方法一:哈希表set去重 思路:我们遍历链表中的每个节点,并将它记录下来;一旦遇到了此前遍历过的节点,就可以判定链表中存在环。借助哈希…...

Android TV开发之VerticalGridView
Android TV应用开发和手机应用开发是一样的,只是多了焦点控制,即选中变色。 androidx.leanback.widget.VerticalGridView 继承 BaseGridView , BaseGridView 继承 RecyclerView 。 所以 VerticalGridView 就是 RecyclerView ,使…...

SpringBoot+Vue项目添加腾讯云人脸识别
一、引言 人脸识别是一种基于人脸特征进行身份认证和识别的技术。它使用计算机视觉和模式识别的方法,通过分析图像或视频中的人脸特征,例如脸部轮廓、眼睛、鼻子、嘴巴等,来验证一个人的身份或识别出他们是谁。 人脸识别可以应用在多个领域…...

什么是IPv4?什么又是IPv6?
IPv4网络IPv4地址 IPv6网络IPv6地址 路由总结感谢 💖 hello大家好😊 IPv4网络 IPv4(Internet Protocol Version 4)是当今互联网上使用的主要网络协议。 IPv4地址 IPv4 地址有32位,通常使用点号分隔的四个十进制八位…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
