PHP8的匿名函数-PHP8知识详解
php 8引入了匿名函数(Anonymous Functions),它是一种创建短生命周期的函数,不需要命名,并且可以在其作用域内直接使用。以下是在PHP 8中使用匿名函数的知识要点:

1、创建匿名函数,语法格式如下:
$fn = function() { // 匿名函数的代码
};
使用function关键字创建一个匿名函数。下面是一个示例:
<?php
$fn = function($arg1, $arg2) { // 匿名函数的代码 return $arg1 + $arg2;
};
echo $fn(3, 4);
?>
以上代码在PHP8中输出的结果为:
7在上述示例中,我们向匿名函数传递了值 $arg1 = 3 和 $arg2 = 4,并输出结果为 7。请根据您的需求修改参数的值。
2、匿名函数可以作为变量赋值给其他变量,也可以作为参数传递给其他函数或方法。示例代码:
<?php
// 将匿名函数赋值给变量
$myFunction = function($arg1, $arg2) {// 匿名函数的代码return $arg1 + $arg2;
};// 使用变量中的匿名函数进行计算
$result = $myFunction(3, 4);
echo $result; // 输出 7
echo "<br>";// 将匿名函数作为参数传递给其他函数或方法
function operate($a, $b, $func) {return $func($a, $b);
}$result = operate(5, 2, function($x, $y) {return $x * $y;
});echo $result; // 输出 10?>在PHP8中运行的结果为:
7
10
在上面的示例中,我们首先将匿名函数赋值给变量 $myFunction,然后使用该变量调用匿名函数并将结果存储在 $result 变量中。
接下来,我们定义了一个 operate() 函数,它接受三个参数:两个操作数 $a 和 $b,以及一个匿名函数 $func。在 operate() 函数内部,我们通过调用 $func($a, $b) 来执行传递进来的匿名函数,并返回其结果。
最后,我们使用了另一个匿名函数作为参数传递给 operate() 函数,并对数字进行相乘操作,将结果输出。
3、匿名函数可以访问其作用域内的变量,这些变量被称为闭包变量(Closure Variables)。在匿名函数内部,可以使用use关键字来引用外部变量。
<?php
$variable = 'php';
$fn = function() use ($variable) { echo $variable;
};
$fn();
?>以上代码在PHP8中,输出的结果为:
php4、匿名函数也可以返回值,就像普通函数一样。可以在匿名函数内部使用return语句来返回值。示范代码:
<?php
$fn = function() { return 'php';
};
echo $fn();
?>以上代码在PHP8中的运行结果为:
php5、匿名函数可以作为回调函数使用,例如在数组排序、异步操作等场景中。可以使用callable类型来指定匿名函数作为回调函数。示范代码:
<?php
$numbers = [4, 2, 8, 6, 1];// 使用匿名函数进行数组排序
usort($numbers, function ($a, $b) {return $a - $b;
});print_r($numbers);
?>在PHP8中运行的结果为:
Array ( [0] => 1 [1] => 2 [2] => 4 [3] => 6 [4] => 8 )
在这个例子中,我们使用了usort函数对$numbers数组进行排序。第二个参数是一个匿名函数,它接受两个参数$a和$b,并返回一个整数值来指定元素之间的比较关系。通过使用匿名函数作为回调函数,我们可以根据自己的逻辑来定义排序规则。
请注意,在使用匿名函数作为回调函数时,可以直接将匿名函数写在函数调用的参数列表中,而不需要定义一个独立的函数体。这样可以使代码更加简洁和易读。
6、匿名函数也可以使用闭包绑定(Closure Binding),即将匿名函数绑定到特定的对象或类。通过使用bind方法,可以将匿名函数绑定到特定的对象上。
示范代码:
<?php
class MyClass {private $message = "Hello";public function sayHello() {$func = function() {echo $this->message;};$boundFunc = $func->bindTo($this, 'MyClass');$boundFunc();}
}$obj = new MyClass();
$obj->sayHello();
?>以上代码在PHP8中运行结果为‘:
Hello
在上述示例中,我们创建了一个名为MyClass的类,该类具有一个私有属性message和一个公共方法sayHello。
在sayHello方法内部,我们定义了一个匿名函数$func,它尝试访问$this->message。然后,我们使用bindTo方法将匿名函数绑定到当前对象$this上,并指定绑定到MyClass类。
最后,我们调用绑定后的函数$boundFunc(),这样就可以在匿名函数中成功访问到$this->message的值。
请注意,这里的关键是使用bindTo方法将匿名函数与特定的对象或类进行绑定。这样做的好处是,匿名函数仍然保持其原始定义中访问外部作用域变量的能力,同时又能够正确地访问绑定的对象或类的成员。
7、匿名函数还可以使用闭包模拟(Closure Simulation),即创建一个模拟闭包来访问外部变量。这在使用旧版本的PHP时非常有用,因为匿名函数在旧版本中不可用。通过使用命名函数和命名函数的变量绑定,可以模拟闭包的行为。示范代码:
<?php
function createClosure($outerVariable) {return function() use ($outerVariable) {echo "Outer variable value: " . $outerVariable;};
}// 创建一个模拟闭包
$closure = createClosure("Hello, world!");// 执行闭包
$closure();
?>在php8zhon运行的结果为:
Outer variable value: Hello, world!
8、静态匿名函数
匿名函数允许被定义为静态化。这样可以防止当前类自动绑定到它们身上,对象在运行时也可能不会被绑定到它们上面。示范代码:
<?php
class MyClass {private static $message = 'Hello';public function testCallback() {$callback = static fn() => self::$message;echo $callback(); // 输出:Hello}
}$obj = new MyClass();
$obj->testCallback();
?>在上面的代码中,我们将匿名函数定义为静态化,并通过static fn() => self::$message创建了一个闭包。该闭包能够访问类内部的私有静态变量$message。在testCallback()方法中,我们调用了该闭包,并输出了结果。
请注意,由于我们使用了静态化的匿名函数,所以无需依赖于对象进行绑定,但仍然可以访问类的成员变量。
相关文章:

PHP8的匿名函数-PHP8知识详解
php 8引入了匿名函数(Anonymous Functions),它是一种创建短生命周期的函数,不需要命名,并且可以在其作用域内直接使用。以下是在PHP 8中使用匿名函数的知识要点: 1、创建匿名函数,语法格式如下&…...

Redis—Redis介绍(是什么/为什么快/为什么做MySQL缓存等)
一、Redis是什么 Redis 是一种基于内存的数据库,对数据的读写操作都是在内存中完成,因此读写速度非常快,常用于缓存,消息队列、分布式锁等场景。 Redis 提供了多种数据类型来支持不同的业务场景,比如 String(字符串)、…...
C语言链表梳理-2
链表头使用结构体:struct Class 链表中的每一项使用结构体:struct Student#include <stdio.h>struct Student {char * StudentName;int StudentAge;int StudentSex;struct Student * NextStudent; };struct Class {char *ClassName;struct Stude…...
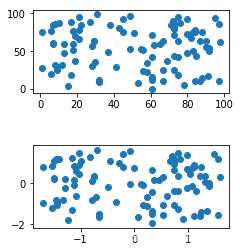
【深度学习】实验03 特征处理
文章目录 特征处理标准化归一化正则化 特征处理 标准化 # 导入标准化库 from sklearn.preprocessing import StandardScalerfrom matplotlib import gridspec import numpy as np import matplotlib.pyplot as plt import warnings warnings.filterwarnings("ignore&quo…...

基于Dpabi的功能连接
1.预处理 这里预处理用Gretna软件进行,共分为以下几步: (1)DICOM转NIfTI格式 (2)去除前10个时间点(Remove first 10 times points):由于机器刚启动、被试刚躺进去也还需适应环境,导致刚开始扫描的数据很…...

在React项目是如何捕获错误的?
文章目录 react中的错误介绍解决方案后言 react中的错误介绍 错误在我们日常编写代码是非常常见的 举个例子,在react项目中去编写组件内JavaScript代码错误会导致 React 的内部状态被破坏,导致整个应用崩溃,这是不应该出现的现象 作为一个框架…...

基于内存池的 简单高效的数据库 SDK简介
基于内存池的 简单高效的数据库 SDK简介 下载地址: https://gitee.com/tankaishuai/powerful_sdks/tree/master/shm_alloc_db_heap shm_alloc_db_heap 是一个基于内存池实现的简单高效的文件型数据存储引擎,利用它可以轻松地像访问内存块一样读、写、增…...
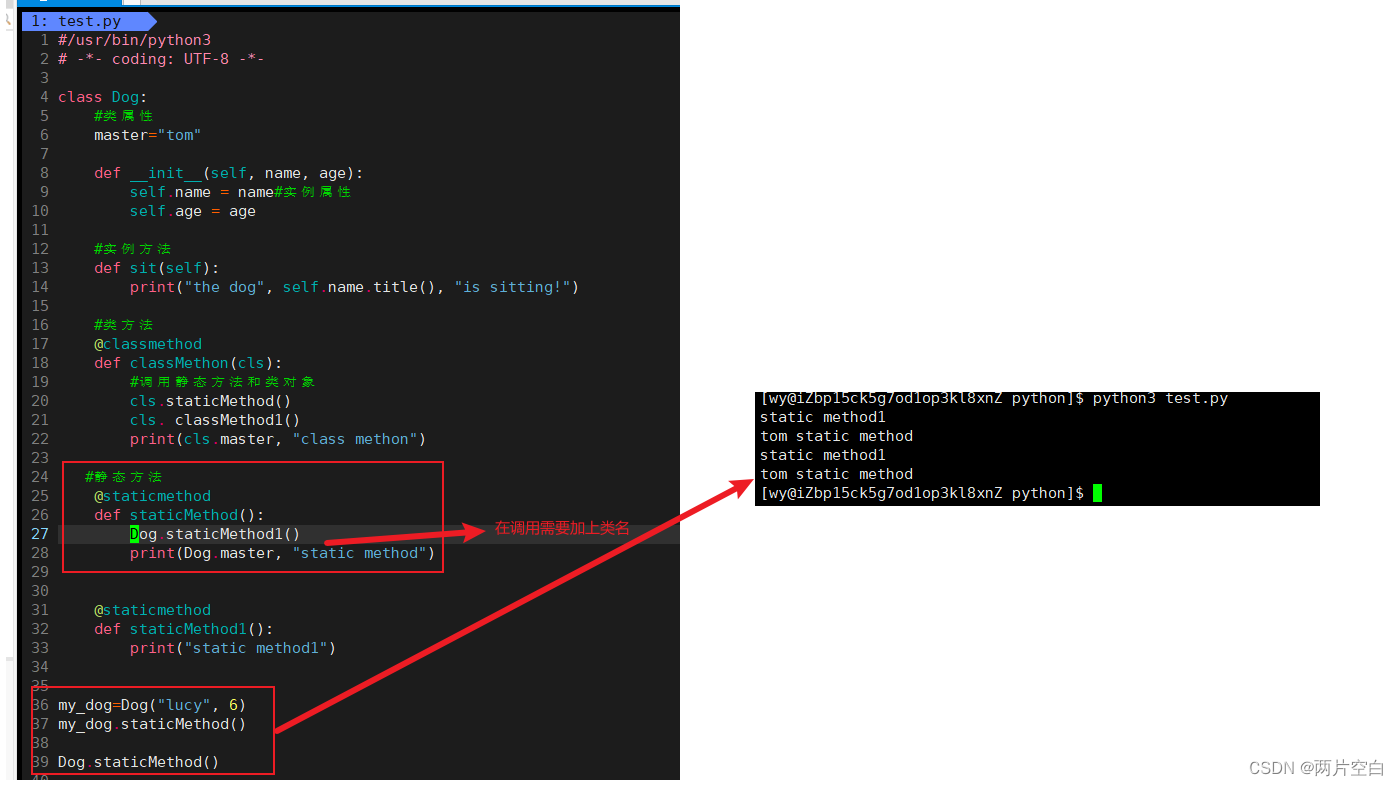
python实例方法,类方法和静态方法区别
为python中的装饰器 实例方法 实例方法时直接定义在类中的函数,不需要任何修饰。只能通过类的实例化对象来调用。不能通过类名来调用。 类方法 类方法,是类中使用classmethod修饰的函数。类方法在定义的时候需要有表示类对象的参数(一般命名为cls&#…...
:使用pyecharts绘制3D折线图)
Pyecharts教程(四):使用pyecharts绘制3D折线图
Pyecharts教程(四):使用pyecharts绘制3D折线图 作者:安静到无声 个人主页 目录 Pyecharts教程(四):使用pyecharts绘制3D折线图准备工作数据准备绘制3D折线图推荐专栏在这篇文章中,我们将学习如何使用pyecharts库来绘制一个3D折线图。pyecharts是一个用于生成Echarts图表的…...
【stable-diffusion使用扩展+插件和模型资源(下)】
插件模型魔法图片等资源:https://tianfeng.space/1240.html 书接上文:(上) 插件推荐 1.lobe theme lobe theme是一款主题插件,直接可以在扩展安装 界面进行了重新布局,做了一些优化,有兴趣的…...

一文了解SpringBoot中的Aop
目录 1.什么是Aop 2.相关概念 3.相关注解 4.为什么要用Aop 5.Aop使用案例 1.什么是Aop AOP:Aspect Oriented Programming,面向切面,是Spring三大思想之一,另外两个是 IOC-控制反转 DI-依赖注入 (Autowired、Qualifier、Re…...
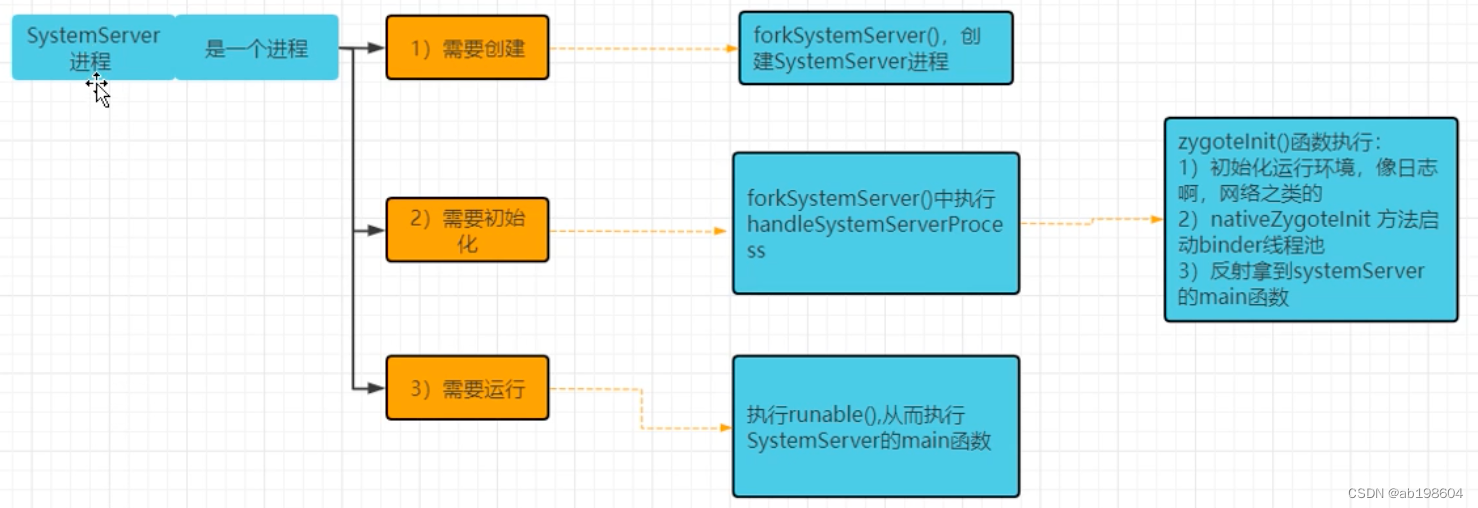
android系统启动流程之zygote如何创建SystemServer进程
SystemServer:是独立的进程,主要工作是管理服务的,它将启动大约90种服务Services. 它主要承担的职责是为APP的运行提供各种服务,像AMS,WMS这些服务并不是一个独立的进程, 它们其实都是SystemServer进程中需要管理的的众多服务之一…...
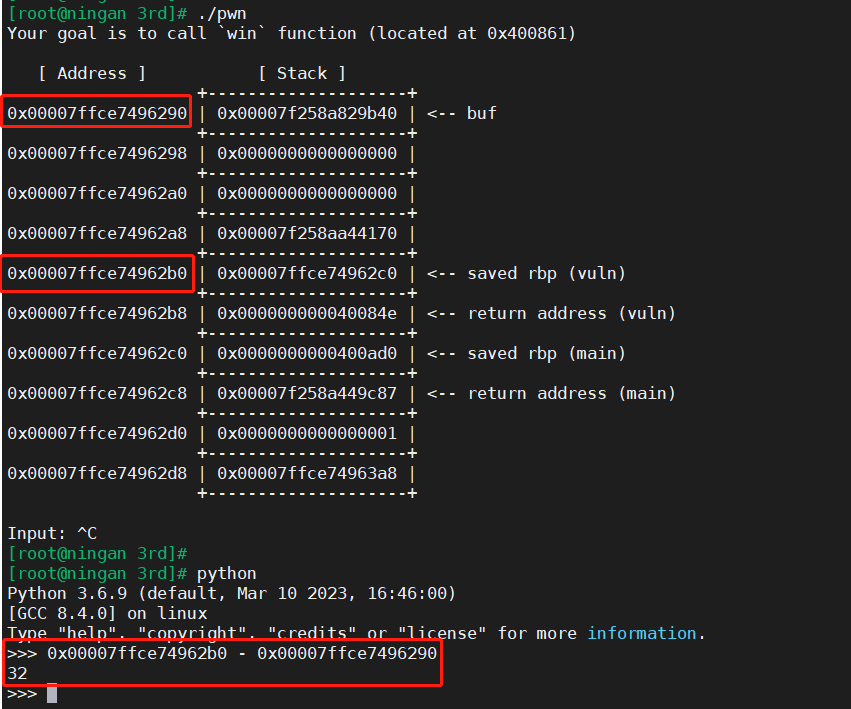
【awd系列】Bugku S3 AWD排位赛-9 pwn类型
文章目录 二进制下载检查分析运行二进制ida分析解题思路exp 二进制下载 下载地址:传送门 检查分析 [rootningan 3rd]# file pwn pwn: ELF 64-bit LSB executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, for …...

vcomp140.dll丢失的修复方法分享,电脑提示vcomp140.dll丢失修复方法
今天,我的电脑出现了一个奇怪的问题,打开某些程序时总是提示“找不到vcomp140.dll文件”。这个问题让我非常头疼,因为我无法正常使用电脑上的一些重要软件。为了解决这个问题,我在网上查找了很多资料,并尝试了多种方法…...
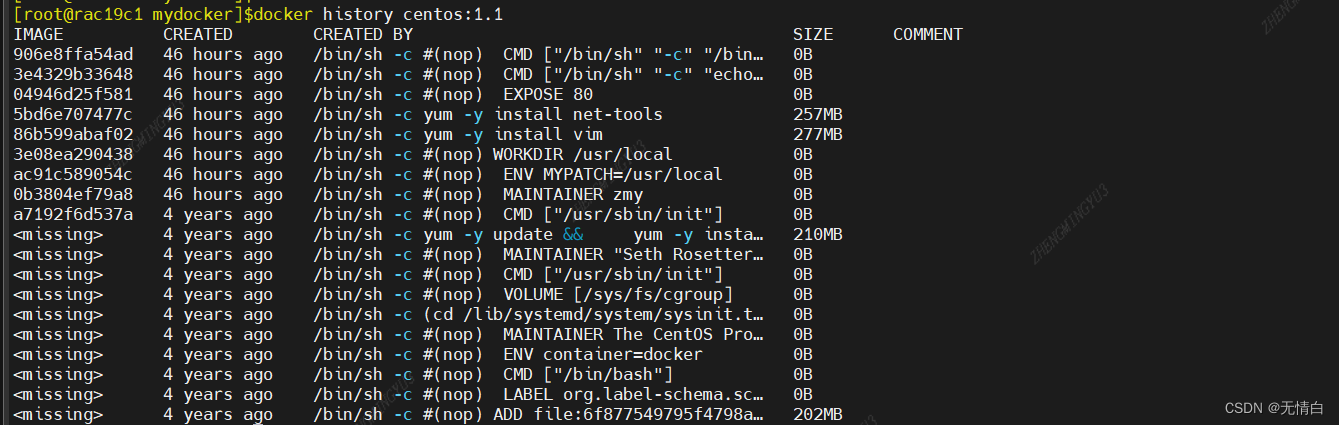
Docker file解析
文章目录 简介构建的三步骤Docker执行Dockerfile的大致流程DockerFile常用保留字指令创建第一个Dockerfile镜像的缓存特性 Docker file 解析 简介 Dockerfile是用来构建Docker镜像的文本文件,是由一条条构建镜像所需的指令和参数构成的脚本,记录了镜像构…...

工作与身体健康之间的平衡
大厂裁员,称35岁以后体能下滑,无法继续高效率地完成工作;体重上涨,因为35岁以后新陈代谢开始变慢;甚至坐久了会腰疼、睡眠困扰开始加重,在众多的归因中,仿佛35岁的到来,会为一切的焦…...

算法和数据结构
STL 【C】蓝桥杯必备 算法竞赛常用STL万字总结_蓝桥杯算法竞赛_Cpt1024的博客-CSDN博客 day1 1:正确 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 // 中序遍历一遍二叉树,并统计节点数目 class Solution { public:int c…...
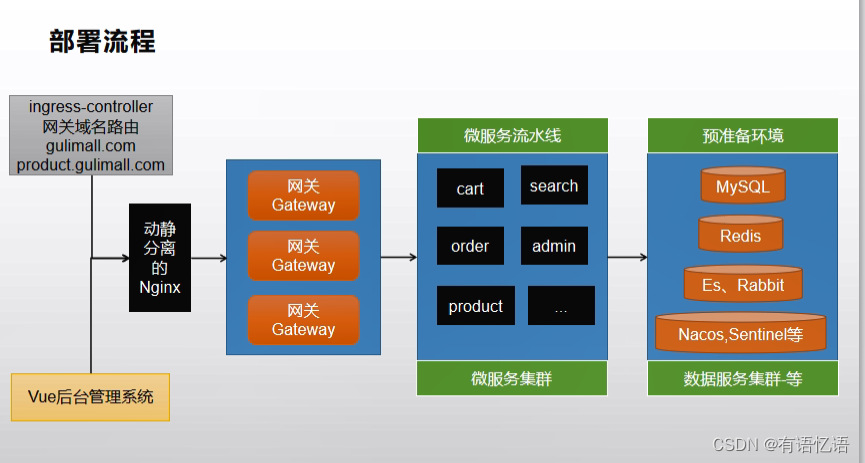
商城-学习整理-集群-K8S-集群环境部署(二十四)
目录 一、MySQL集群1、mysql集群原理2、Docker安装模拟MySQL主从复制集群1、下载mysql镜像2、创建Master实例并启动3、创建 Slave 实例并启动4、为 master 授权用户来同步数据1、进入 master 容器2、进入 mysql 内部 (mysql –uroot -p)3、查看 master 状…...
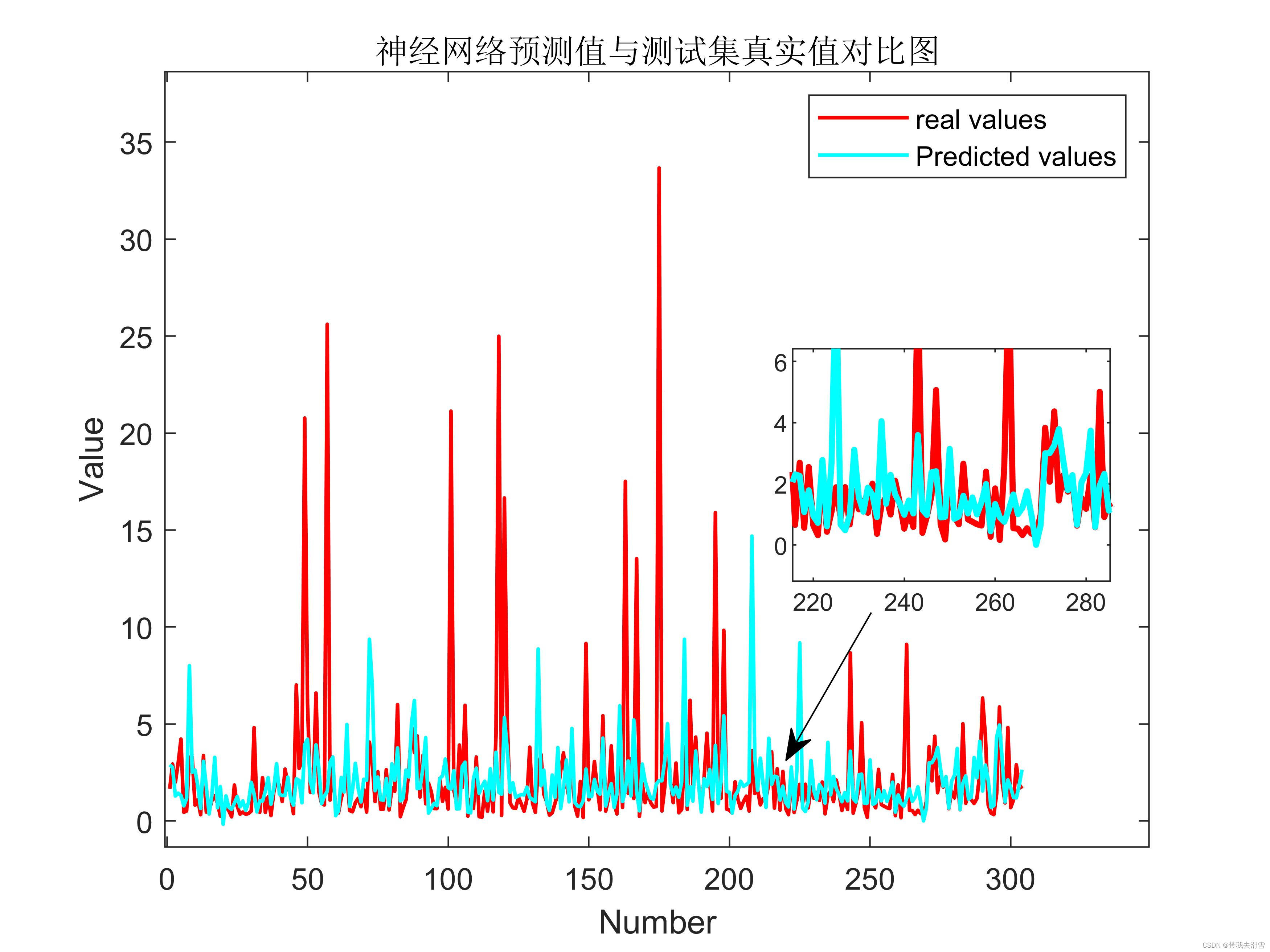
利用多种机器学习方法对爬取到的谷歌趋势某个关键词的每日搜索次数进行学习
大家好,我是带我去滑雪! 前一期利用python爬取了谷歌趋势某个关键词的每日搜索次数,本期利用爬取的数据进行多种机器学习方法进行学习,其中方法包括:随机森林、XGBOOST、决策树、支持向量机、神经网络、K邻近等方法&am…...
ARL资产侦察灯塔 指纹增强
项目:https://github.com/loecho-sec/ARL-Finger-ADD 下载项目后运行 python3 ARl-Finger-ADD.py https://你的vpsIP:5003/ admin password该项目中的finger.json可以自己找到其他的指纹完善,然后运行脚本添加指纹。...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
