matlab实现牛顿迭代法求解非线性方程
非线性方程是指含有未知数的方程,且方程中至少有一个未知数的次数大于一或者含有非一次幂的函数(如指数、对数、三角函数等)。例如,$f(x) = x^3 - 2x - 5 = 0$就是一个非线性方程。非线性方程通常没有显式的解析解,因此需要使用数值方法来近似求解。
牛顿迭代法(Newton's method)是一种常用的数值方法,它利用函数的导数来构造一个迭代序列,逐步逼近方程的根。牛顿迭代法的基本思想是:假设$f(x)$在某个初始点$x_0$附近有根$x^*$,则可以用$f(x)$在$x_0$处的切线来近似$f(x)$,并求出切线与$x$轴的交点$x_1$作为下一个近似值。然后重复这个过程,直到满足某个收敛条件。
牛顿迭代法的迭代公式为:
$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$
其中,$f'(x)$表示$f(x)$的导数,$n$表示迭代次数。
为了使用matlab实现牛顿迭代法,我们需要定义以下几个要素:
- 非线性方程$f(x)$及其导数$f'(x)$
- 初始点$x_0$
- 收敛条件(如最大迭代次数、误差容限等)
下面是一个使用matlab实现牛顿迭代法求解$f(x) = x^3 - 2x - 5 = 0$的示例代码:
% 定义非线性方程及其导数
f = @(x) x^3 - 2*x - 5;
fp = @(x) 3*x^2 - 2;% 定义初始点
x0 = 2;% 定义最大迭代次数和误差容限
maxiter = 100;
tol = 1e-6;% 初始化迭代次数和误差
iter = 0;
err = inf;% 进行牛顿迭代
while iter < maxiter && err > tol% 计算下一个近似值x1 = x0 - f(x0)/fp(x0);% 计算误差err = abs(x1 - x0);% 更新迭代次数和初始点iter = iter + 1;x0 = x1;
end% 输出结果
if err <= tolfprintf('方程的根为:%.6f\n', x1);fprintf('迭代次数为:%d\n', iter);
elsefprintf('未达到收敛条件\n');
end运行上述代码,得到输出结果为:
方程的根为:2.094551
迭代次数为:5可以看出,牛顿迭代法在5次迭代后就达到了收敛条件,并得到了方程的一个根。当然,这个结果可能会随着初始点和收敛条件的不同而有所变化。牛顿迭代法的优点是收敛速度快,缺点是需要知道函数的导数,并且可能会遇到奇点或者震荡的情况。
相关文章:

matlab实现牛顿迭代法求解非线性方程
非线性方程是指含有未知数的方程,且方程中至少有一个未知数的次数大于一或者含有非一次幂的函数(如指数、对数、三角函数等)。例如,$f(x) x^3 - 2x - 5 0$就是一个非线性方程。非线性方程通常没有显式的解析解,因此需…...

Cpp学习——编译链接
目录 编辑 一,两种环境 二,编译环境下四个部分的 1.预处理 2.编译 3.汇编 4.链接 三,执行环境 一,两种环境 在程序运行时会有两种环境。第一种便是编译环境,第二种则是执行环境。如下图: 在程序运…...

android - fragment 数据丢失?状态丢失?
最佳答案 一些状态丢失的例子: 1. 假设您有一个按钮和一个 TextView 。在代码中,你已经定义了初始值为 0 的整数 i,它通过单击按钮递增 1,并且它的值显示在 TextView 中。假设你已经按下按钮 5 次,那么 textview 将被设置为 0。也…...

Git基本操作
本地仓库 当我们初始化(git init)之后,会在当前目录下生成一个与项目并列的.git文件夹,当我们对项目作出更改之后使用git commit命令,一般是将修改提交到本地仓库,也就是该文件夹下面的文件会对应修改&…...

Nginx配置文件详解
Nginx配置文件详解 1、Nginx配置文件1.1主配置文件详解1.2子配置文件 2、全局配置部分2.1修改启动的工作进程数(worker process) 优化2.2cpu与worker process绑定2.3 PID 路径修改2.4 修改工作进程的优先级2.5调试工作进程打开的文件的个数2.6关闭master-worker工作…...
进程启动原理(1))
【0217】stats collector(统计信息收集器)进程启动原理(1)
文章目录 1. 启动 stats collector进程1.1 stats collector进程启动过程1.1.1 检查套接字 pgStatSock 是否存在1.1.2 重新启动失败的stats collector频率1.1.3 fork() 三种返回值处理1.2 detach所有共享内存段1.3 detach 共享内存段1.4 stats collecotr进程启动的主体相关阅读:…...
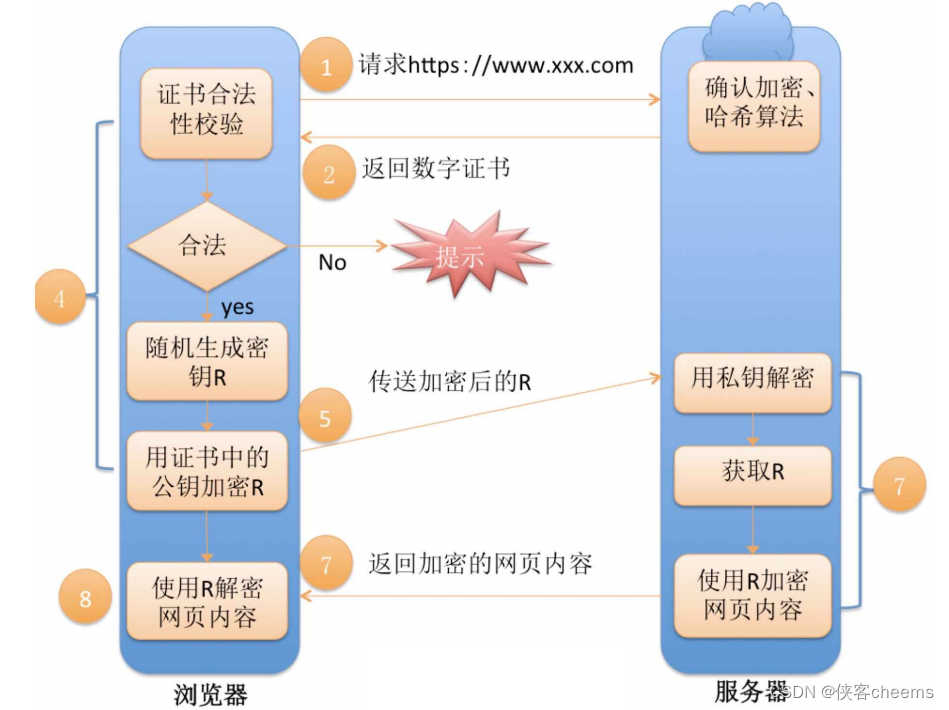
【应用层】网络基础 -- HTTPS协议
HTTPS 协议原理加密为什么要加密常见的加密方式对称加密非对称加密 数据摘要&&数据指纹 HTTPS 的工作过程探究方案1-只使用对称加密方案2-只使用非对称加密方案3-双方都使用非对称加密方案4-非对称加密对称加密中间人攻击-针对上面的场景 CA认证理解数据签名方案5-非对…...
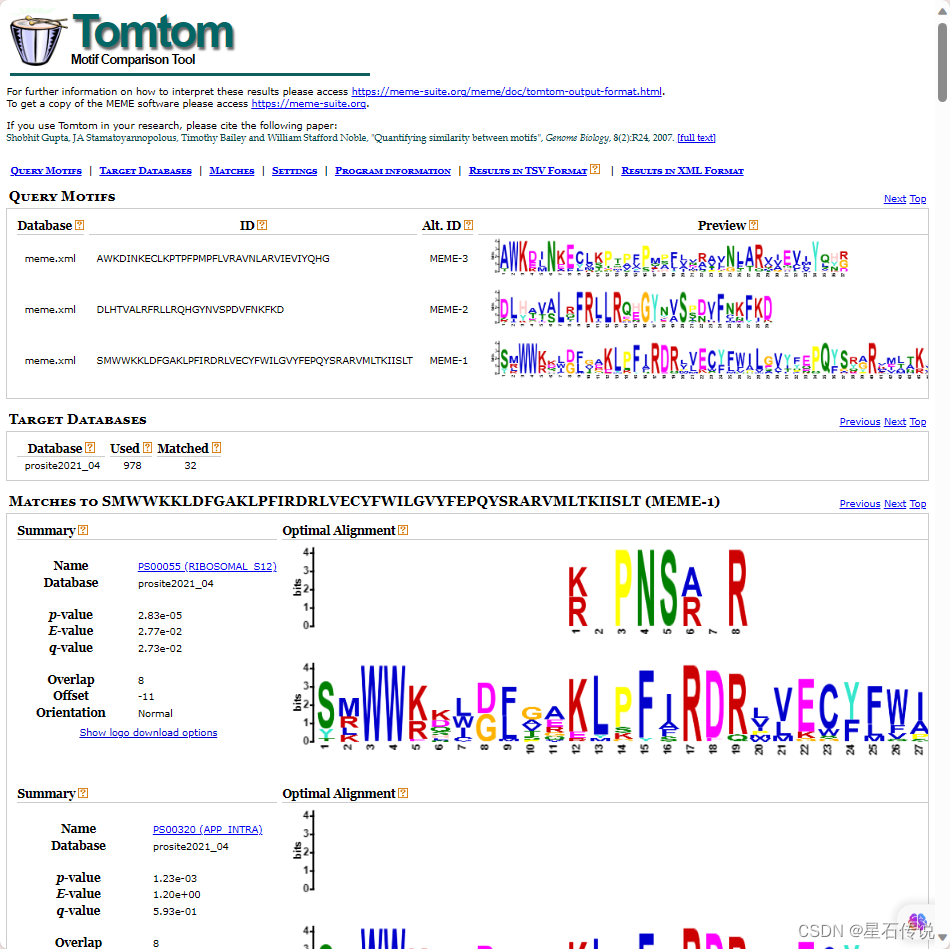
实验篇—— 基因家族Motif 分析
实验篇—— 基因家族Motif 分析 文章目录 前言一、名词解释二、实操1. MEME工具箱2. Motif Discovery(基序发现)1. 结果网页2. 在TBtools中(额外) 2. Motif Enrichment(基序富集分析)3. Motif Search&#…...

Linux拓展之阻止或禁用普通用户登录
禁止指定用户登录 chsh -s /sbin/nologin 指定用户名示例 chsh -s /sbin/nologin testuser恢复指定用户登录 chsh -s /bin/bash 指定用户名示例 chsh -s /bin/bash testuser参考 https://blog.csdn.net/cnds123321/article/details/125232580 https://www.cnblogs.com/cai…...

Linux系统USB摄像头测试程序(四)_视频旋转及缩放
下面的程序实现了视频的旋转及缩放,窗口中点击鼠标左键视频向左旋转,点击鼠标右键视频向右旋转并且视频缩小了二分之一。程序中首先把yvyv422转换成了RGB24,然后利用opencv进行了旋转和缩放,其后用sdl2进行了渲染。使用了ffmpeg、…...
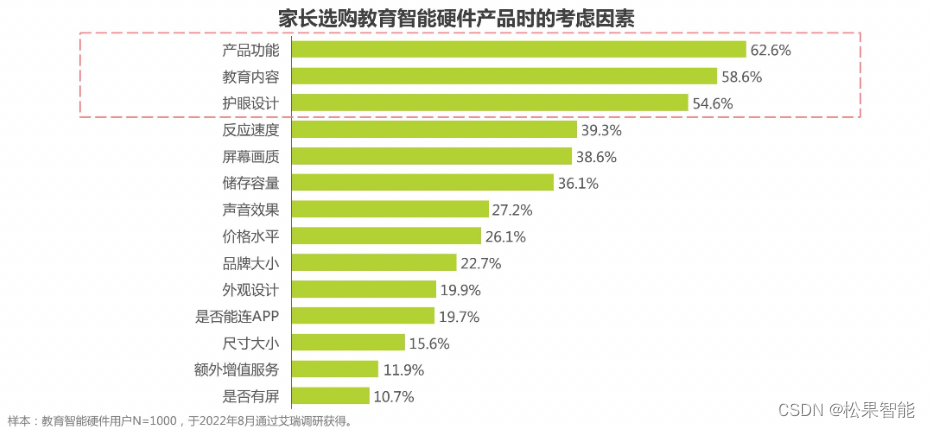
大模型+学习机,是概念游戏还是双向奔赴?
众所周知,2023年上半年大模型概念炙手可热。各大科技公司纷纷卷入,或宣称布局相关领域,或率先官宣自研大模型。而随着资本市场对大模型概念的热情有所消退,属于这片战场的新一轮角逐慢慢聚焦在了技术的落地应用上。 8月15日&#…...

linux怎么查看用户属于哪个组
查看当前用户所属组 shell> groups root查看指定用户所属组 shell> groups testuser testuser : testusershell> id testuser uid1000(testuser) gid1000(testuser) groups1000(testuser)查看组文件 shell> cat /etc/group...

邂逅JavaScript
前言:前端三大核心 前端开发最主要需要掌握的是三个知识点:HTML、CSS、JavaScript 一、认识编程语言 1.计算机语言 前面我们已经学习了HTML和CSS很多相关的知识: 在之前我们提到过, HTML是一种标记语言, CSS也是一种样式语言; 他们本身都是属于计算…...

Android 中 Fragment判空
1. 判断 Fragment 是否已经被添加到 Activity 中,可以通过 Fragment 的 isAdded() 方法来判断。 2. 判断 Fragment 的 View 是否已经被创建,可以通过 Fragment 的 getView() 方法来判断。 3. 判断 Fragment 是否已经被销毁,可以通过 Fragme…...

软考高级系统架构设计师系列论文八十八:财务数据仓库系统的设计与实现
软考高级系统架构设计师系列论文八十八:财务数据仓库系统的设计与实现 一、摘要二、正文三、总结一、摘要 近年来,数据仓库技术在信息系统的建设中得到了广泛应用,有效地为决策提供了支持。2020年6月,本人所在单位组织开发了财务管理决策系统,该系统主要是使高层领导掌握企…...
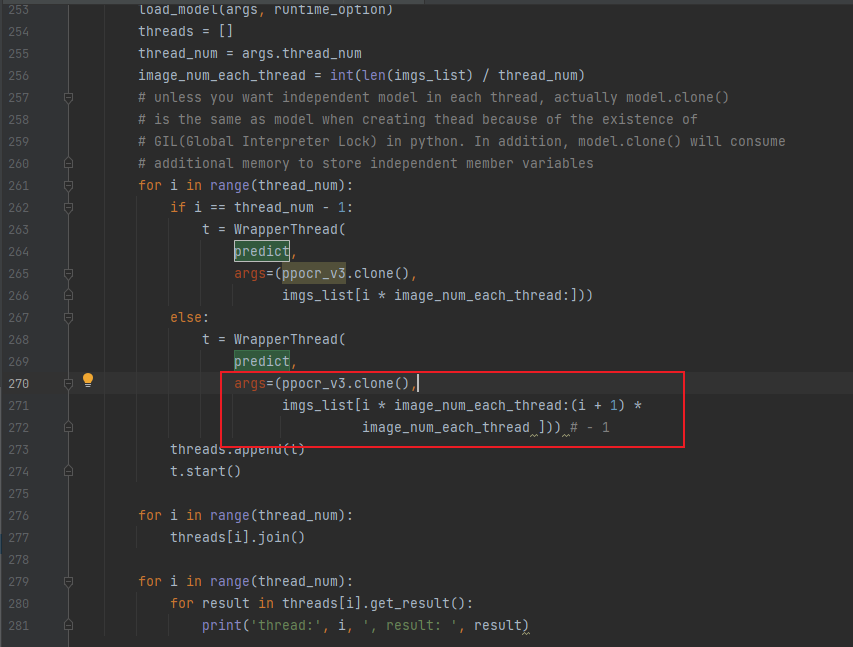
fastdeploy部署多线程/进程paddle ocr(python flask框架 )
部署参考:https://github.com/PaddlePaddle/FastDeploy/blob/develop/tutorials/multi_thread/python/pipeline/README_CN.md 安装 cpu: pip install fastdeploy-python gpu :pip install fastdeploy-gpu-python #下载部署示例代码 git cl…...
【图论】拓扑排序
一.定义 拓扑排序是一种对有向无环图(DAG)进行排序的算法,使得图中的每个顶点在排序中都位于其依赖的顶点之后。它通常用于表示一些任务之间的依赖关系,例如在一个项目中,某些任务必须在其他任务之前完成。 拓扑排序的…...
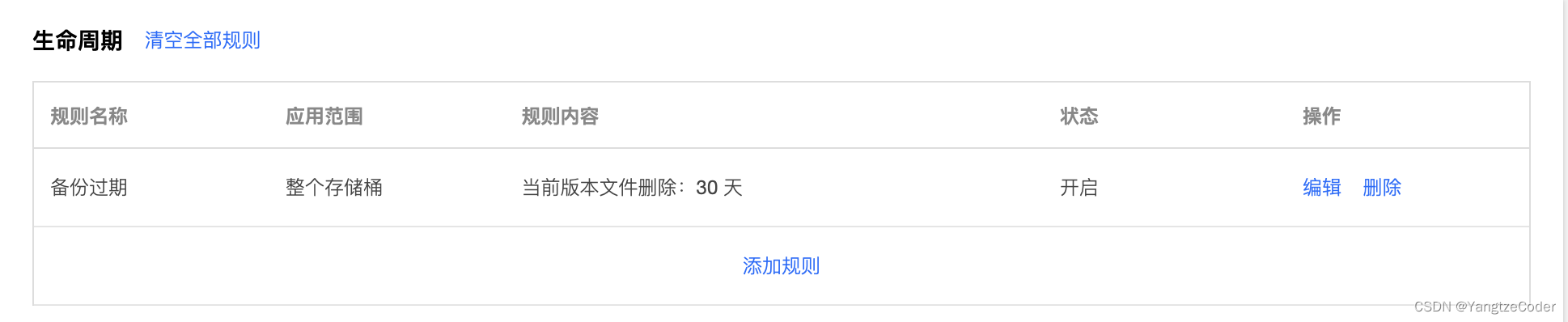
自动化备份方案
背景说明 网上有很多教程,写的都是从零搭建一个什么什么,基本上都是从无到有的教程,但是,很少有文章提及搭建好之后如何备份,这次通过请教GitHub Copilot Chat,生成几个备份脚本,以备后用。 注…...
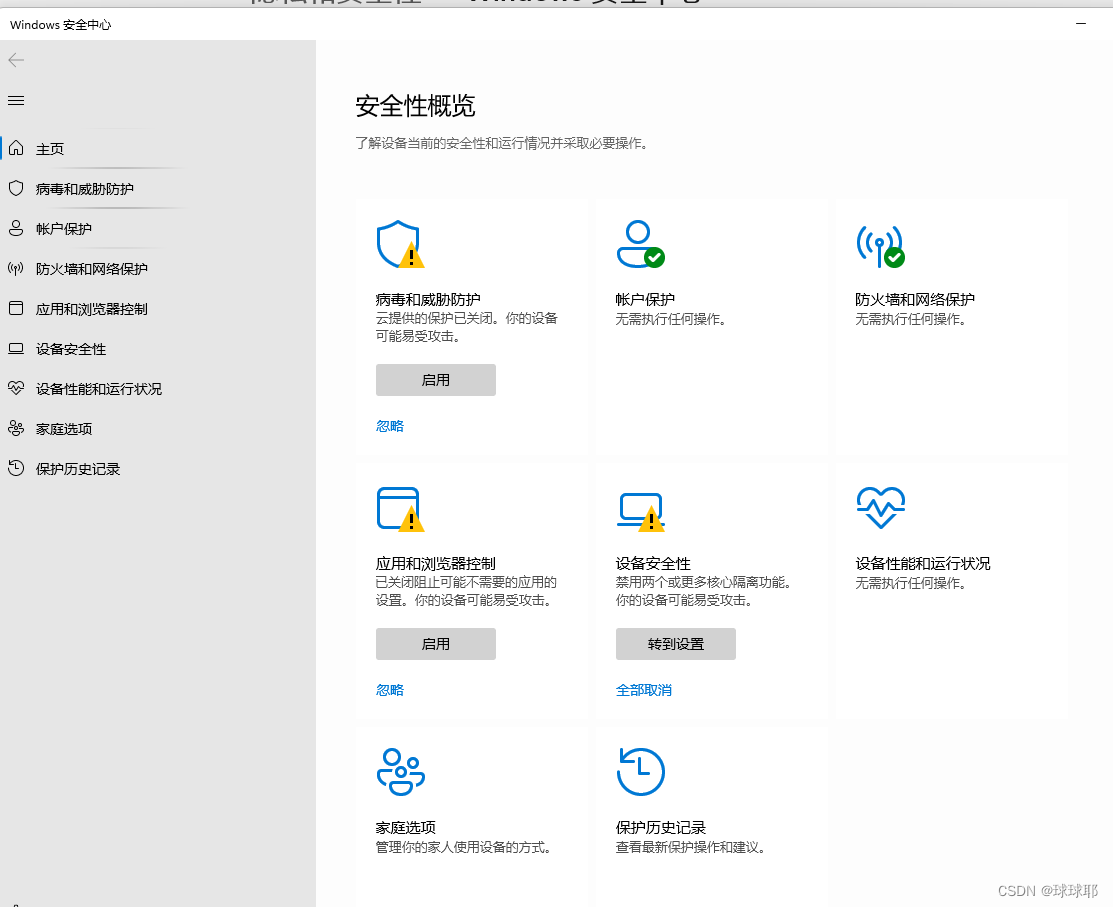
win11出现安全中心空白和IT管理员已限制对此应用的某些区域的访问
问题 windows安全中心服务被禁用 winr 输入services.msc 找到windows安全中心服务查看是否被禁用,改为启动,不可以改动看第三条 打开设置,找到应用—windows安全中心–终止–修复–重置 重启如果还是不行看第四条 家庭版系统需要打开gped…...

github实用指令(实验室打工人入门必备)
博主进入实验室啦,作为一只手残党决定在这里分享一些常用的github使用情景和操作指南来解救其他手残党。 内容随着情景增加实时更新。如果只有没几个内容说明场景不多(相信对手残党而言是再好不过的消息) 情景一:…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
