【牛客刷题专栏】0x0B:JZ3 数组中重复的数字(C语言编程题)
前言
- 个人推荐在牛客网刷题(点击可以跳转),它登陆后会保存刷题记录进度,重新登录时写过的题目代码不会丢失。
- 个人刷题练习系列专栏:个人CSDN牛客刷题专栏。 题目来自:牛客/题库 / 在线编程 / 剑指offer:

目录
- 前言
- 问题描述:
- 举例:
- 解法思路:
- 代码结果:
- 结束语
问题描述:
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组[2,3,1,0,2,5,3],那么对应的输出是2或者3。存在不合法的输入的话输出-1。
数据范围:0≤n≤10000
进阶:时间复杂度O(n),空间复杂度O(n)
举例:
//输入:
[2,3,1,0,2,5,3]
//返回值:
2
//说明:2或3都是对的
解法思路:
-
只需要重新设计一个等长的数组,用于计数原题目中给出的数组元素出现的次数,最后返回相应的数组元素。
-
如果没有说“长度为n的数组里的所有数字都在0到n-1范围内”,那就需要设计一个大范围的数组或者动态数组。
代码结果:
/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param numbers int整型一维数组 * @param numbersLen int numbers数组长度* @return int整型*/
int duplicate(int* numbers, int numbersLen ) {int num[10000];//数据范围:0≤n≤10000int i;//数组初始化for(i=0;i<numbersLen;i++){num[i] = 0;}//按照给定的number数组,对应的num数组进行计数,计算有多少个重复的数字for(i=0;i<numbersLen;i++){num[numbers[i]]++;}for(i=0;i<numbersLen;i++){if(num[numbers[i]]>1)return numbers[i];}return -1;
}
结束语
- 以上就是该C语言编程题的内容。可以在牛客尝试刷几道题目来练习实践。牛客网刷题(点击可以跳转),可以尝试注册使用。
- 题目来自:牛客/题库 / 在线编程 / 剑指offer:

相关文章:

【牛客刷题专栏】0x0B:JZ3 数组中重复的数字(C语言编程题)
前言 个人推荐在牛客网刷题(点击可以跳转),它登陆后会保存刷题记录进度,重新登录时写过的题目代码不会丢失。个人刷题练习系列专栏:个人CSDN牛客刷题专栏。 题目来自:牛客/题库 / 在线编程 / 剑指offer: 目录前言问题…...
js中的隐式类型转换有哪些
目录一、隐式类型转换条件二、 的隐式类型转换三、 的隐式类型转换四、object 的隐式类型转换探讨 object 的隐式转换执行顺序探讨 Symbol.toPrimitive 属性如何将对象转换为原始值在前端js这门动态弱类型语言中,不仅存在着显示类型转换,还存在许多隐式类…...

WuThreat身份安全云-TVD每日漏洞情报-2023-02-17
漏洞名称:IBM Aspera Faspex 预身份验证 RCE 漏洞 漏洞级别:高危 漏洞编号:CVE-2022-47986 相关涉及:IBM Aspera Faspex 漏洞状态:POC 参考链接:https://tvd.wuthreat.com/#/listDetail?TVD_IDTVD-2023-02805 漏洞名称:Kardex Mlog MCC PATH 遍历 漏洞级别:严重 漏洞编号:CVE…...
水平分库分表常见策略range、hash)
掌握MySQL分库分表(三)水平分库分表常见策略range、hash
文章目录range策略Range策略延伸基于Range范围分库分表业务场景hash取模案例规则水平分库分表,根据什么规则进行划分? range策略 自增id,根据ID范围进行分表(左闭右开) 规则案例: 1~1,000,000 是 table…...

CTFer成长之路之CTF中的SQL注入
CTF中的SQL注入CTF SQL注入 SQL注入-1 题目描述: 暂无 docker-compose.yml version: 3.2services:web:image: registry.cn-hangzhou.aliyuncs.com/n1book/web-sql-1:latestports:- 80:80启动方式 docker-compose up -d 题目Flag n1book{union_select_is_so_cool} Wri…...

python snap7读写PLC
主要在DB块里操作 读DB块 import snap7 import structdef plc_connection():PLC_IP 192.168.10.10PLC snap7.client.Client()PLC.connect(PLC_IP, rack0, slot1)return PLCPLC plc_connection()PLC.read_area()方法从PLC中读取指定区域的数据。 1200表示DB块的编号&#x…...

使用物联网进行智能能源管理的10大优势
如今,物联网推动了许多行业的自动化流程和运营效率,而物联网在能源领域的应用尤其受到消费者、企业甚至政府的关注。除了对电力供应链的诸多好处之外,物联网能源管理系统还让位于新的智能电网,并有望实现更高的安全性和效率。基于…...
工业4.0和工业物联网如何协同工作
虽然许多公司已经接受了工业物联网,但他们现在必须接受工业4.0对数据驱动的数字化转型的承诺。随着制造业、能源、公用事业和供应链应用迅速采用工业物联网(IIoT),这些行业的新现实正在形成。工业物联网提供了企业管理数千个活动部件所需的数据类型&…...
Python机器学习入门笔记(3)—— 线性回归
目录 线性回归 算法简述 LinearRegression() API SGDRegressor API LinearRegression() 和 SGDRegressor对比 过拟合与欠拟合 岭回归 应用场景 线性回归 算法简述 线性回归是一种基本的机器学习算法,它用于建立自变量和因变量之间的线性关系模型。它假设…...

Java:顶级Java应用程序服务器 — Tomcat、Jetty、GlassFish、WildFly
如果你想编写Java web应用程序,首先需要做出一个艰难的决定:选择运行应用程序的Java应用程序服务器。什么是应用服务器?一般来说,应用程序服务器执行Java应用程序。在操作系统中启动它们,然后将应用程序部署到其中。将应用程序服…...
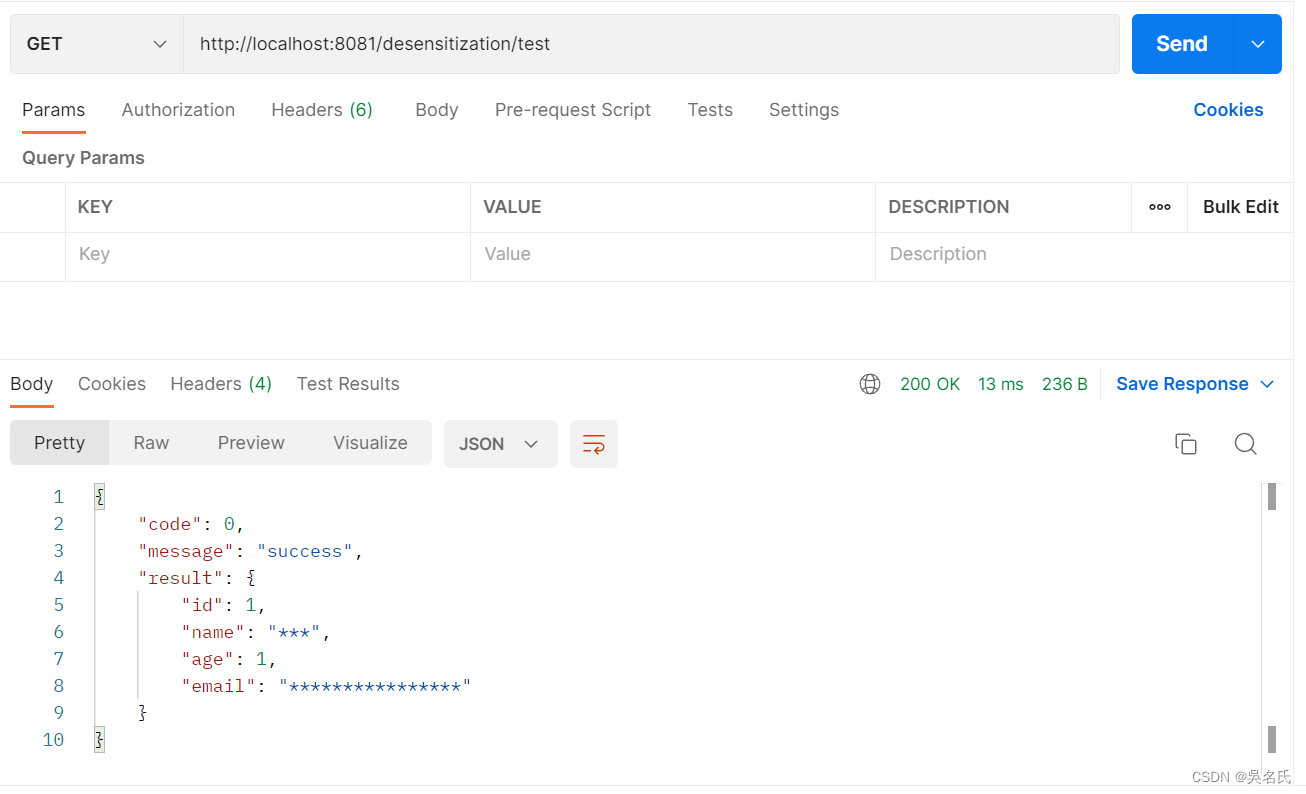
如何在SpringBoot项目上让接口返回数据脱敏,一个注解即可
1 背景需求是某些接口返回的信息,涉及到敏感数据的必须进行脱敏操作2 思路①要做成可配置多策略的脱敏操作,要不然一个个接口进行脱敏操作,重复的工作量太多,很显然违背了“多写一行算我输”的程序员规范。思来想去,定…...
python 之 海龟绘图(turtle)
注:从个人博客园移植而来 使用简介 python 2.6引入的一个简单的绘图工具,俗称为海龟绘图。3.x以上使用的话,可通过pip进行安装,命令为: pip/pip3 install turtle如果出现如下错误: 解决方式: …...
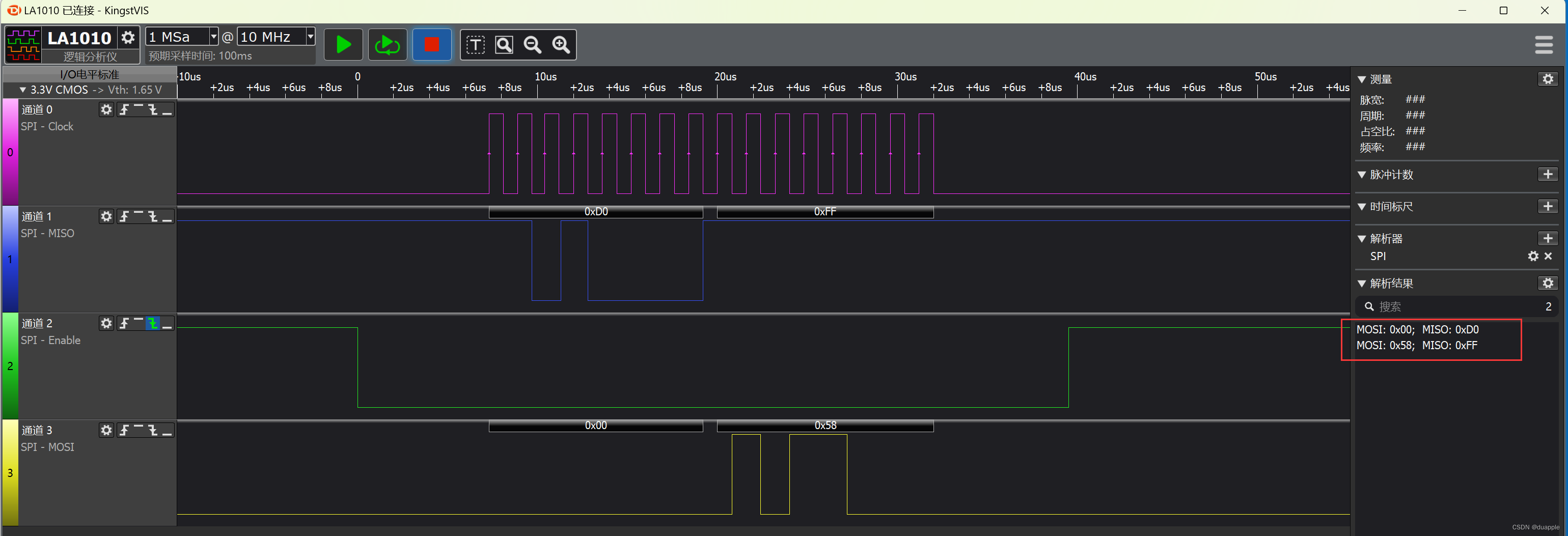
RT-Thread SPI使用教程
RT-Thread SPI 使用教程 实验环境使用的是正点原子的潘多拉开发板。 SPI从机设备使用的是BMP280温湿度大气压传感器。 使用RT-Thread Studio搭建基础功能。 1. 创建工程 使用RT-Thread Studio IDE创建芯片级的工程。创建完成后,可以直接编译下载进行测试。 2.…...

shiro使用——整合spring
shiro使用——整合spring 1. 引入相关配置 <dependency><groupId>org.apache.shiro</groupId><artifactId>shiro-spring</artifactId><version>1.9.1</version></dependency>2. 自定义Realm类 继承AuthorizingRealm 并重写相…...

2023-02-20 leetcode-AccountsMerge
摘要: 记录对leetcode-AccountsMerge的反思 要求: Given a list accounts, each element accounts[i] is a list of strings, where the first element accounts[i][0] is a name, and the rest of the elements are emails representing emails of the account. * Now, w…...

中国高速公路行业市场规模及未来发展趋势
中国高速公路行业市场规模及未来发展趋势编辑中国高速公路行业市场规模正在迅速增长。随着中国经济的快速发展和城市化的加速,对交通基础设施的需求也在不断增加。高速公路是最有效的交通工具,可以大大缩短交通时间,提高出行效率。因此&#…...
佳能iC MF645CX彩色激光多功能打印机报E302-0001故障码检修
故障现象: 一台佳能iC MF645CX彩色激光多功能一体机开机报E302-0001故障代码,如果设备未恢复,请联系经销商或客户支持中心。 维修分析: 佳能iC MF645CX彩色激光多功能一体机开机报E302-0001故障代码的...

加密越来越简单——用JavaScript实现数据加密和解密
加密越来越简单——用JavaScript实现数据加密和解密概念常用算法1. MD5加密算法2. SHA-1加密算法3. AES加密算法代码示例结论总结在当今互联网的世界中,安全性越来越受到关注,数据加密成为了必不可少的一环。Javascript作为前端开发的主要语言之一&#…...

线程池的使用场景
学习整理线程池的使用场景。...

图像分割算法
图像分割算法阈值分割固定阈值自适应阈值大津阈值(OTSU)最大熵阈值连通域分析区域生长分水岭阈值分割、连通域分析、区域生长、分水岭 阈值分割 固定阈值、自适应阈值(adaptiveThreshold)、大津阈值(OTSU)、最大熵阈值(KSW) 固定阈值 固定阈值的调用函数: //Input…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
