当前位置： 首页 > news >正文

element-ui table表格滚动条拉到最右侧 表头与内容不能对齐

news 2026/2/8 23:25:48

1.问题概述

当表格数据太多，会出现纵向滚动条和横向滚动条，把横向滚动条拉到最右侧时，会出现表头与内容不能对齐的现象。

2.解决方法
1.当页面数据加载完毕后，在后面加上

this.$nextTick(() => {this.$refs.table.doLayout();
})

2.别忘了给表格加上ref属性

<el-table ref="table"></el-table>

相关文章：

element-ui table表格滚动条拉到最右侧 表头与内容不能对齐

1.问题概述 当表格数据太多&#xff0c;会出现纵向滚动条和横向滚动条&#xff0c;把横向滚动条拉到最右侧时&#xff0c;会出现表头与内容不能对齐的现象。 2.解决方法 1.当页面数据加载完毕后&#xff0c;在后面加上 this.$nextTick(() > {this.$refs.table.doLayout()…...

编程日记 2023/8/29 6:39:23

React中的性能测试工具组件Profiler的基本使用

React中的性能测试工具组件Profiler是一个非常有用的工具&#xff0c;它可以帮助我们分析React应用程序的性能瓶颈。在本文中&#xff0c;我们将学习如何使用Profiler组件来测试React应用程序的性能。 首先&#xff0c;让我们来了解一下Profiler组件的基本用法。在React中&…...

编程日记 2023/8/29 6:38:22

提升生产效率，降低运维成本：纺织业物联网网关应用

在众多物联网技术应用中纺织业正逐渐崭露头角。物联网技术通过无线连接纺织设备、PLC、传感器&#xff0c;实现了纺织厂的生产数据信息的远程监控和数据采集、远程管理&#xff0c;为企业提供了更高效、智能的生产方式。智联物联小编在本文中将重点介绍纺织业物联网的应用与通讯…...

编程日记 2023/8/29 6:37:21

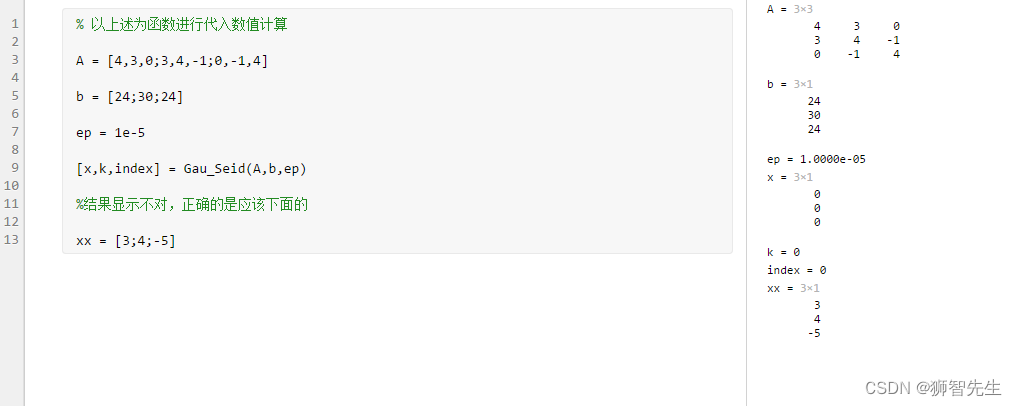
【学习笔记】求解线性方程组的G-S迭代法

求解线性方程组的G-S迭代法 // 运行不成功啊function [x,k,index] Gau_Seid(A,b,ep,it_max) % 求解线性方程组的G-S迭代法&#xff0c;其中 % A为方程组的系数矩阵 % b为方程组的右端项 % ep为精度要求&#xff0c;省缺为1e-5 % it_max为最大迭代次数&#xff0c;省缺为100 % …...

编程日记 2023/8/29 6:36:20

Kotlin协程flow缓冲buffer

Kotlin协程flow缓冲buffer 先看一个普通的flow&#xff1a; import kotlinx.coroutines.delay import kotlinx.coroutines.flow.* import kotlinx.coroutines.runBlocking import kotlin.system.measureTimeMillisfun main(args: Array<String>) {val delayTime 100Lru…...

编程日记 2023/8/29 6:35:17

完全免费的GPT，最新整理，2023年8月24日，已人工验证，不用注册，不用登录，更不用魔法，点开就能用

完全免费的ChatGPT&#xff0c;最新整理&#xff0c;2023年8月24日&#xff0c;已人工验证&#xff0c; 不用注册&#xff0c;不用登录&#xff0c;更不用魔法&#xff0c;点开就能用&#xff01; 第一个&#xff1a;网址地址统一放在文末啦&#xff01;文末直达 看上图你就能…...

编程日记 2023/8/29 6:34:15

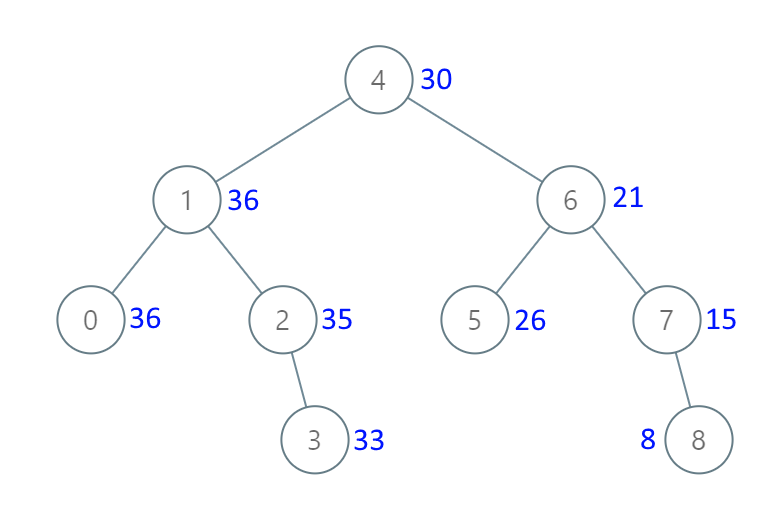
LeetCode538. 把二叉搜索树转换为累加树

538. 把二叉搜索树转换为累加树 文章目录 [538. 把二叉搜索树转换为累加树](https://leetcode.cn/problems/convert-bst-to-greater-tree/)一、题目二、题解方法一&#xff1a;递归&#xff08;中序遍历与节点更新&#xff09;方法二&#xff1a;反向中序遍历与累加更新&#x…...

编程日记 2023/8/29 6:33:13

TP6 使用闭合语句查询多个or的模型语句

例子&#xff1a;查询出在单位表中所有的小学&#xff0c;初中和高中&#xff1b;其中school_period保存的就是学段数据$where []; $where[] function ($query) {$query->where(school_period, like, %小学%)->whereOr(school_period, like, %初中%)->whereOr(schoo…...

编程日记 2023/8/29 6:32:11

浅析Linux SCSI子系统：设备管理

文章目录 概述设备管理数据结构scsi_host_template&#xff1a;SCSI主机适配器模板scsi_host&#xff1a;SCSI主机适配器主机适配器支持DIF scsi_target&#xff1a;SCSI目标节点scsi_device&#xff1a;SCSI设备 添加主机适配器构建sysfs目录 添加SCSI设备挂载LunIO请求队列初…...

编程日记 2023/8/29 6:31:10

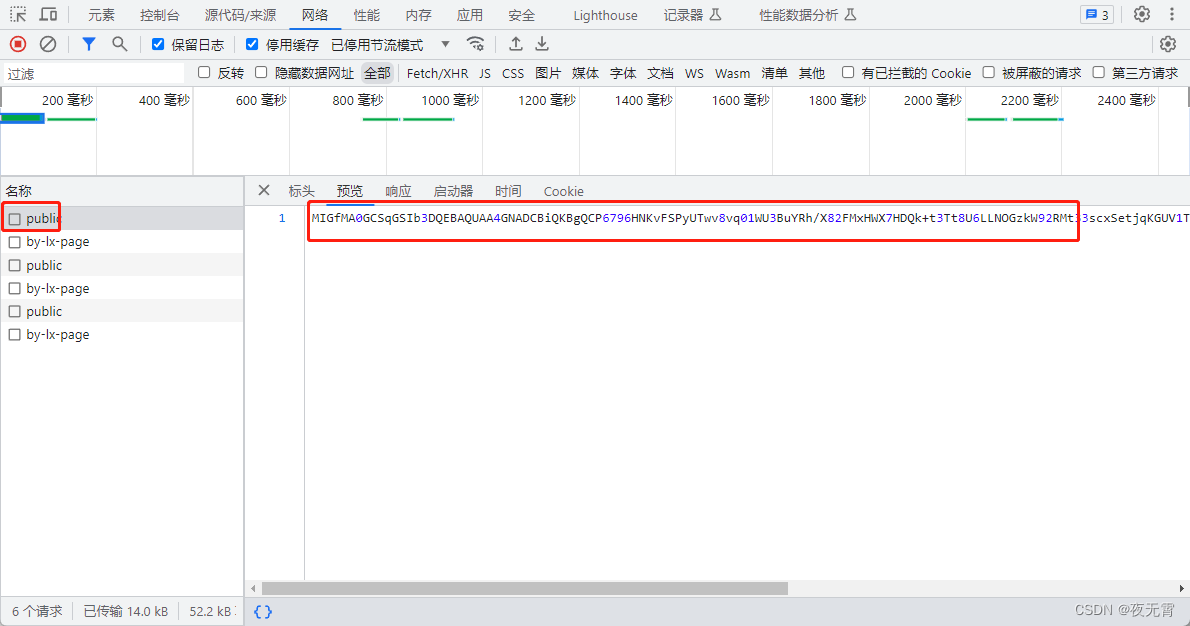
爬虫逆向实战（二十五）--某矿采购公告

一、数据接口分析 主页地址&#xff1a;某矿 1、抓包 通过抓包可以发现数据接口是cgxj/by-lx-page 2、判断是否有加密参数 请求参数是否加密&#xff1f; 通过查看“载荷”模块可以发现有一个param的加密参数 请求头是否加密&#xff1f; 无响应是否加密&#xff1f; 无c…...

编程日记 2023/8/29 6:30:09

DPLL 算法之分裂策略

前言 DPLL算法确实是基于树&#xff08;或二叉树&#xff09;的回溯搜索算法&#xff0c;它用于解决布尔可满足性问题&#xff08;SAT问题&#xff09;。下面我会分析您提到的DPLL算法中的分裂策略&#xff0c;以及它是如何在搜索过程中起作用的。 DPLL算法中的分裂策略是用于在…...

编程日记 2023/8/29 6:29:08

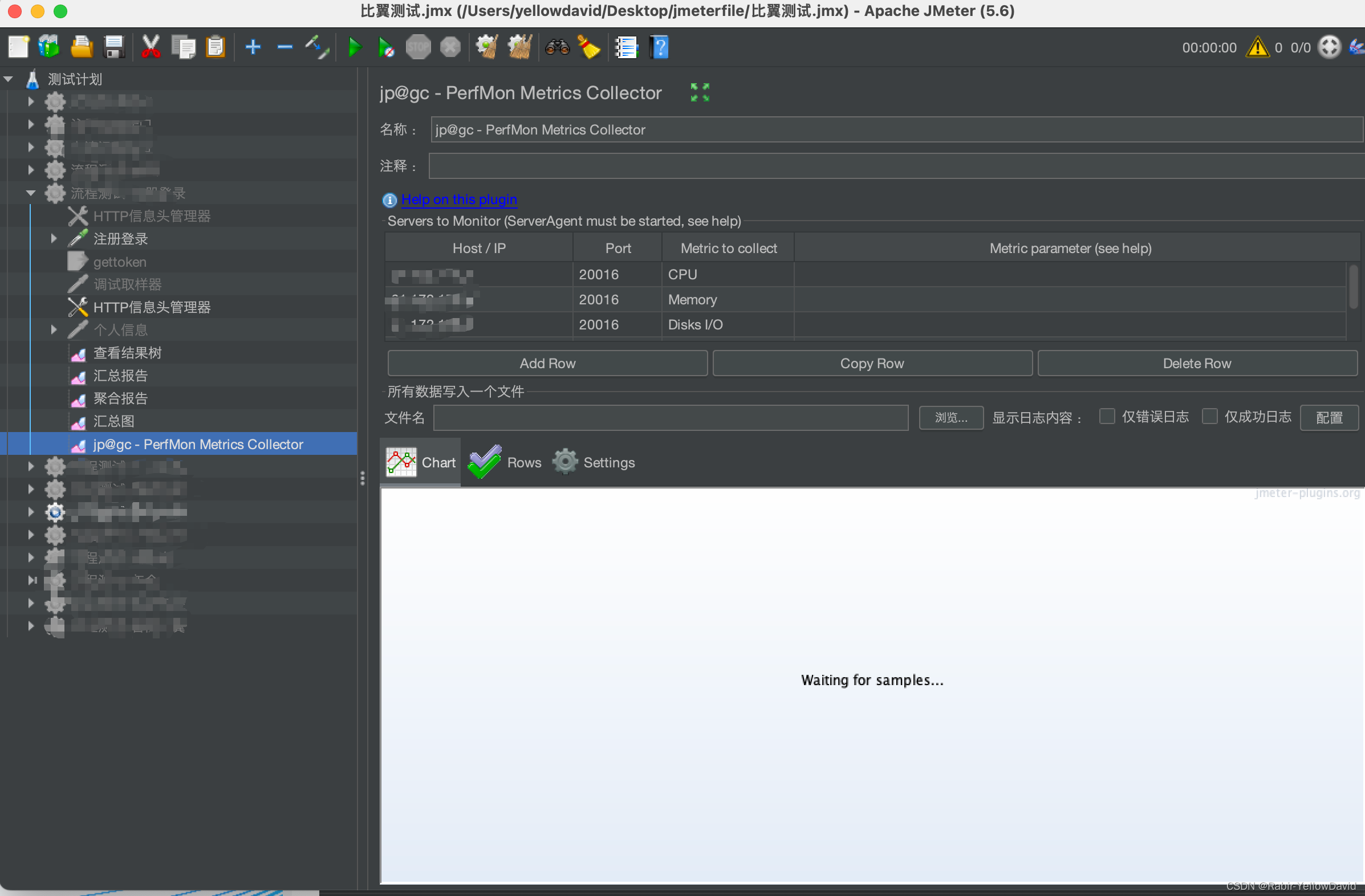
Jmeter+ServerAgent

一、Jmeter 下载 https://jmeter.apache.org/download_jmeter.cgi选择Binaries二进制下载 apache-jmeter-5.6.2.tgz 修改配置文件 jmeter下的bin目录&#xff0c;打开jmeter.properties 文件 languagezh_CN启动命令 cd apache-jmeter-5.6/bin sh jmeter二、ServerAgent 监…...

编程日记 2023/8/29 6:28:06

打破数据孤岛！时序数据库 TDengine 与创意物联感知平台完成兼容性互认

新型物联网实现良好建设的第一要务就是打破信息孤岛&#xff0c;将数据汇聚在平台统一处理&#xff0c;实现数据共享&#xff0c;放大物联终端的行业价值&#xff0c;实现系统开放性&#xff0c;以此营造丰富的行业应用环境。在此背景下&#xff0c;物联感知平台应运而生&#…...

编程日记 2023/8/29 6:27:05

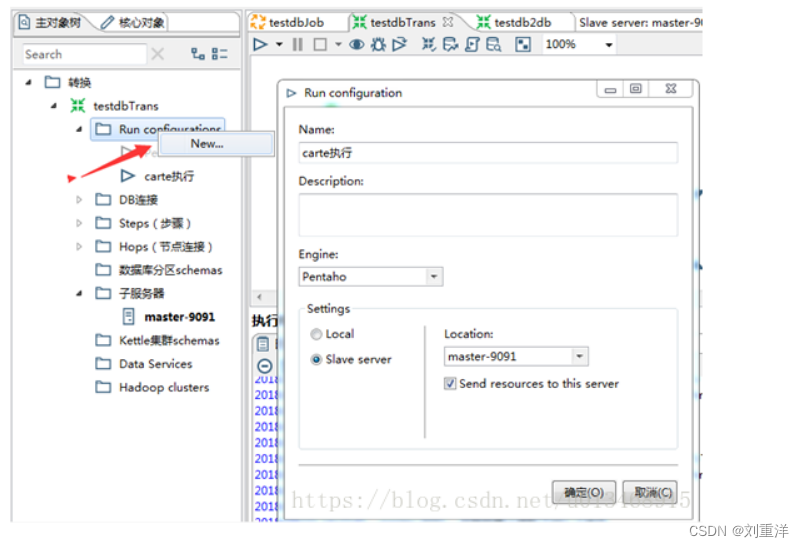
ubuntu22安装和部署Kettle8.2

前提 kettle是纯java编写的etl开源工具&#xff0c;目前kettle7和kettle8都需要java8或者以上才能正常运行。所以运行kettle前先检查java环境是否正确配置&#xff0c;java版本是否是8或者以上。 kettle安装 1、创建kettle目录&#xff0c;并将kettle的zip包解压到kettle目…...

编程日记 2023/8/29 6:26:04

修复 Ubuntu Linux 中的“找不到命令‘python’”错误

在ubuntu 22.04版本中使用 callstack backtrace.txt 回溯错误点是碰到了该问题。 参考文章&#xff1a;链接 ubuntu22.04版本中默认只安装了python3版本 查看python各个版本安装情况&#xff0c;在终端输入命令&#xff1a; type python python2 python3如果安装了对应的版本…...

编程日记 2023/8/29 6:25:01

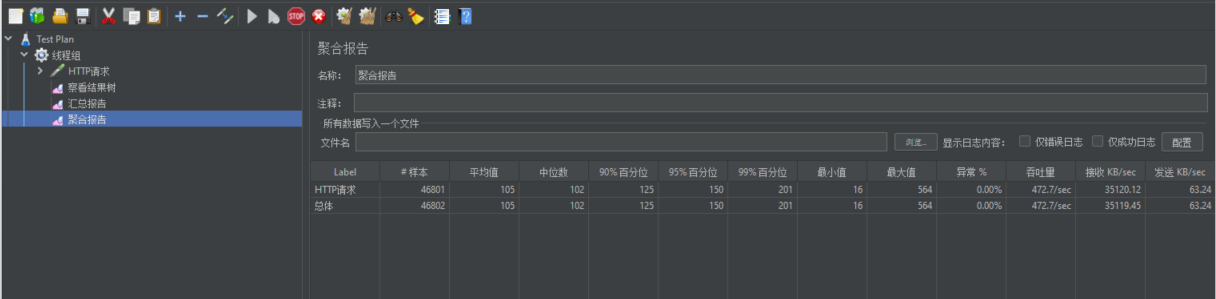
【业务功能篇86】微服务-springcloud-系统性能压力测试-jmeter-性能优化-JVM参数调优

系统性能压力测试 一、压力测试 压力测试是给软件不断加压&#xff0c;强制其在极限的情况下运行&#xff0c;观察它可以运行到何种程度&#xff0c;从而发现性能缺陷&#xff0c;是通过搭建与实际环境相似的测试环境&#xff0c;通过测试程序在同一时间内或某一段时间内&…...

编程日记 2023/8/29 6:23:57

mysql的登录与退出

mysql是c/s架构&#xff0c;意味着同时要有客户端和服务端 1 找到客户端。mysql.exe的安装目录 打开命令行 2 输入对应的服务器的ip&#xff0c;如果是本地&#xff0c;就是Localhost&#xff0c;如果是远程服务器&#xff0c;那就输入对应ip/域名。并且指定mysql监听的端口 …...

编程日记 2023/8/29 6:22:56

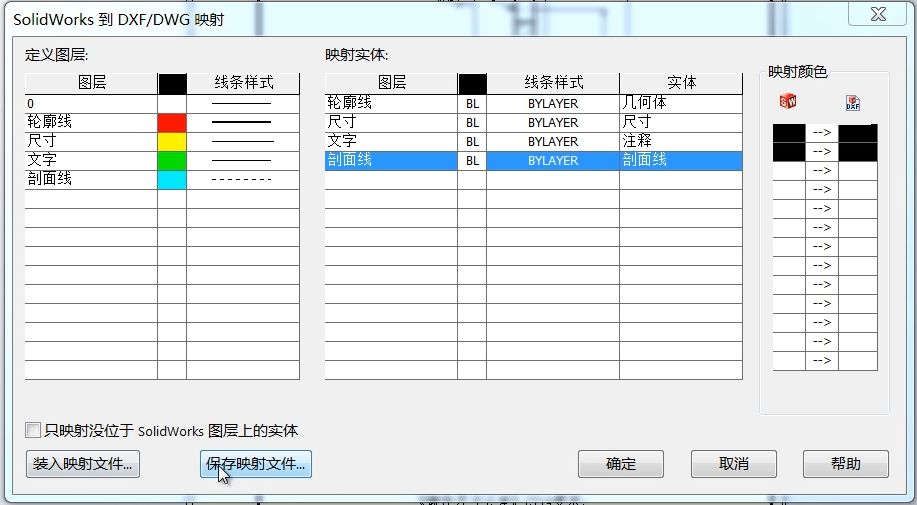
SOLIDWORKS工程图转DWG图层映射技巧

DWG格式的图纸在工程制图中有着非常重要的地位&#xff0c;工程实践中常常就需要将SOLIDWORKS工程图进行转换。对于两者之间数据衔接的妥善处理&#xff0c;是提升工作效率的有效手段。基于此目的&#xff0c;本次我们将介绍数据衔接的一个有效解决方案&#xff1a;图层数据的映…...

编程日记 2023/8/29 6:21:55

PMAC与Modbus主站进行Modbus Tcp通讯

PMAC与Modbus主站进行Modbus Tcp通讯 创建modbus通讯参数 在项目的PMAC Script Language\Global Includes下创建一个名为00_Modbus_Para.pmh的pmh文件。 Modbus[0].Config.ServerPort 0 Modbus[0].Config.ConnectTimeOut 6000 Modbus[0].Config.SendRecvTimeOut 0 Modbu…...

编程日记 2023/8/29 6:20:54

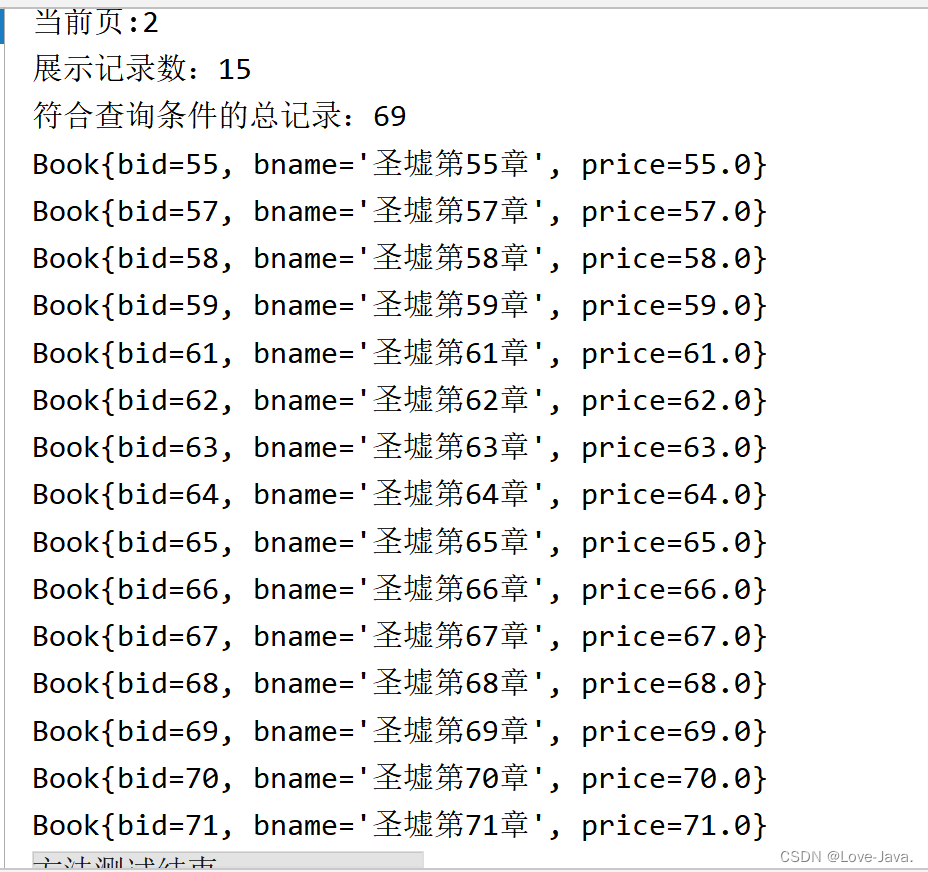
MyBatis分页插件PageHelper的使用及MyBatis的特殊符号---详细介绍

一&#xff0c;分页的概念 分页是一种将大量数据或内容分割成多个页面以便逐页显示的方式。在分页中&#xff0c;数据被分割成一定数量的页&#xff0c;每页显示一部分数据或内容&#xff0c;用户可以通过翻页或跳分页是一种将大量数据或内容分割成多个页面以便逐页显示的方式。…...

编程日记 2023/8/29 6:19:52

XML Group端口详解

在XML数据映射过程中&#xff0c;经常需要对数据进行分组聚合操作。例如&#xff0c;当处理包含多个物料明细的XML文件时&#xff0c;可能需要将相同物料号的明细归为一组&#xff0c;或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码&#xff0c;增加了开…...

编程新知 2026/2/8 4:37:34

华为云AI开发平台ModelArts

华为云ModelArts&#xff1a;重塑AI开发流程的“智能引擎”与“创新加速器”&#xff01; 在人工智能浪潮席卷全球的2025年&#xff0c;企业拥抱AI的意愿空前高涨&#xff0c;但技术门槛高、流程复杂、资源投入巨大的现实&#xff0c;却让许多创新构想止步于实验室。数据科学家…...

编程新知 2026/2/8 4:37:19

设计模式和设计原则回顾

设计模式和设计原则回顾 23种设计模式是设计原则的完美体现，设计原则设计原则是设计模式的理论基石， 设计模式 在经典的设计模式分类中（如《设计模式：可复用面向对象软件的基础》一书中），总共有23种设计模式，分为三大类： 一、创建型模式（5种） 1. 单例模式（Sing…...

编程新知 2025/12/14 20:57:41

2024年赣州旅游投资集团社会招聘笔试真

2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案，答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年，()预言了电磁波的存在，并指出…...

编程新知 2025/12/10 4:08:53

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍，多层嵌套定位示例

文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解（初学者版） 1. static（默认值） 2. relative（相对定位） 3. absolute（绝对定位） 4. fixed（固定定位） 5. sticky（粘性定位） 三、定位元素的层级关系（z-i…...

编程新知 2026/1/26 9:48:34

稳定币的深度剖析与展望

一、引言 在当今数字化浪潮席卷全球的时代&#xff0c;加密货币作为一种新兴的金融现象&#xff0c;正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而&#xff0c;加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下&#xff0c;稳定…...

编程新知 2025/10/24 12:31:26

Selenium常用函数介绍

目录 一&#xff0c;元素定位 1.1 cssSeector 1.2 xpath 二&#xff0c;操作测试对象 三&#xff0c;窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四&#xff0c;弹窗 五&#xff0c;等待 六&#xff0c;导航 七&#xff0c;文件上传 …...

编程新知 2026/1/29 3:55:23

tomcat入门

1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效&#xff0c;稳定&#xff0c;易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

编程新知 2025/7/7 19:44:31

wpf在image控件上快速显示内存图像

wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像&#xff08;比如分辨率3000*3000的图像&#xff09;的办法&#xff0c;尤其是想把内存中的裸数据&#xff08;只有图像的数据&#xff0c;不包…...

编程新知 2026/1/31 9:25:11

面试高频问题

文章目录 &#x1f680; 消息队列核心技术揭秘&#xff1a;从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"&#xff1f;性能背后的秘密1.1 顺序写入与零拷贝&#xff1a;性能的双引擎1.2 分区并行&#xff1a;数据的"八车道高速公路"1.3 页缓存与批量处理…...

编程新知 2025/11/17 0:00:05